SIGNALS SYSTEMS ENT 281 Chapter 3 Fourier Series





























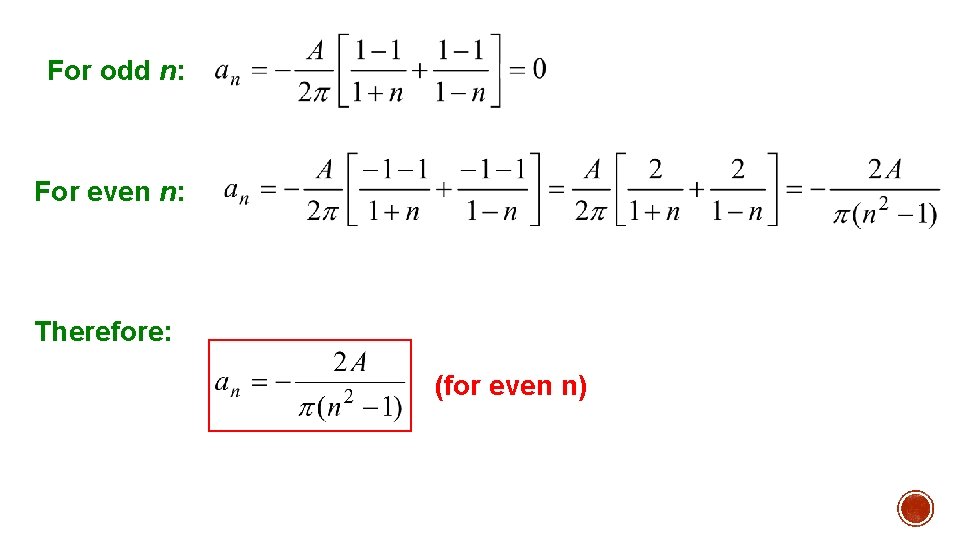
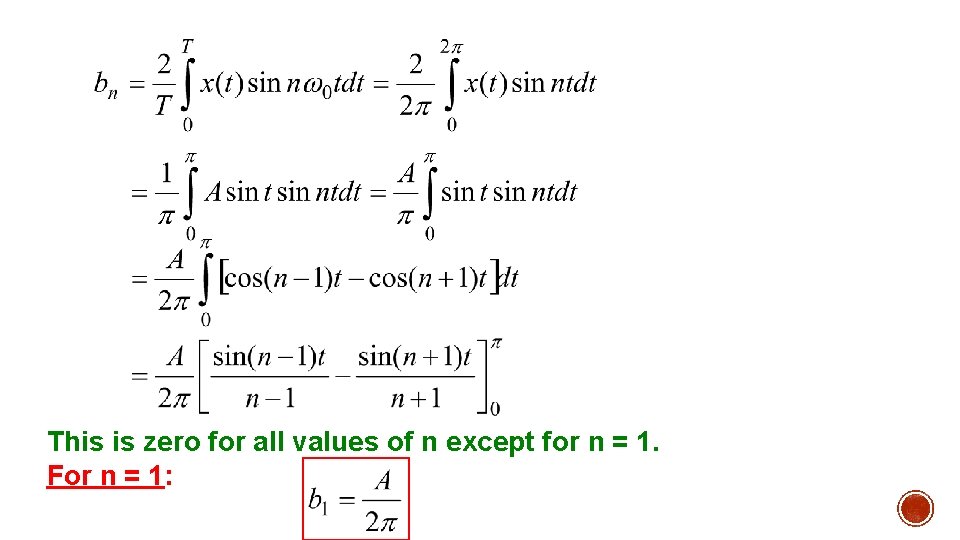


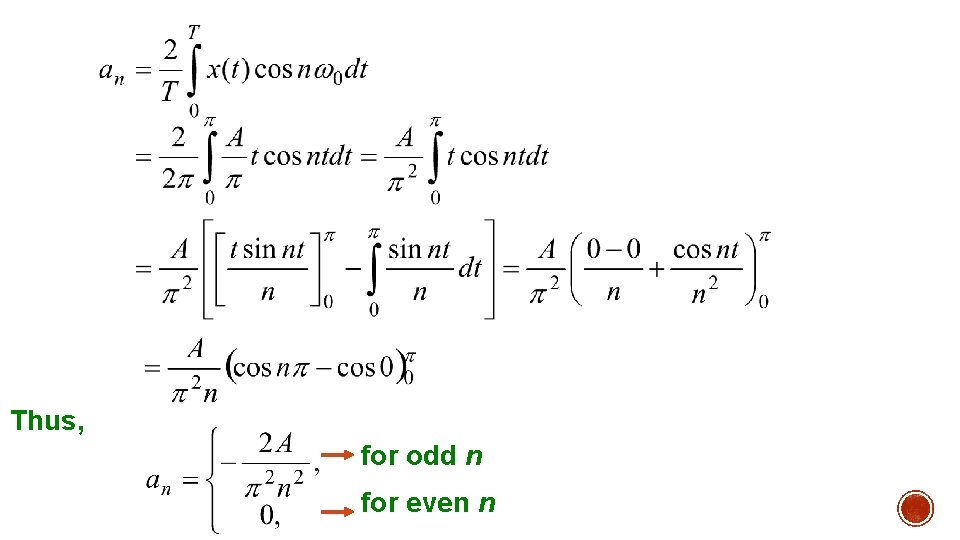

















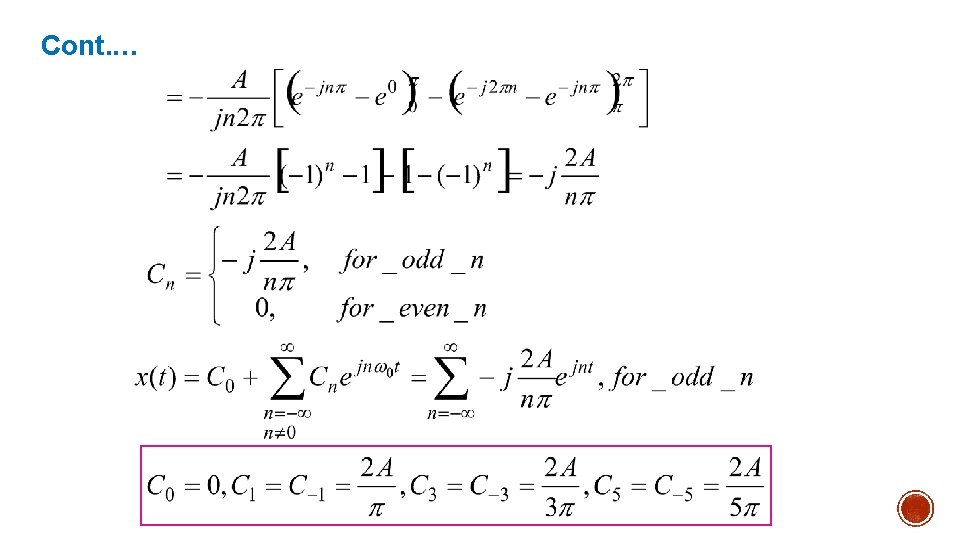










- Slides: 78

SIGNALS & SYSTEMS (ENT 281) Chapter 3: Fourier Series DR. HASIMAH ALI SCHOOL OF MECHATRONIC ENGINEERING UNIVERSITY MALAYSIA PERLIS

3. 1 INTRODUCTION 1. The representation of a periodic signal in terms of complex exponentials, or equivalently in terms of sine and cosine waveforms, leads to the Fourier series that are used extensively used in all fields of science and engineering. 2. The Fourier series is named after the French physicist Jean Baptiste Fourier (1768 -1830) –who was the first to suggest – periodic signals could be represented by a sum of sinusoids. 3. Introduction of representation. the concept of frequency-domain 4. We learn how to decompose periodic signals into their frequency components.

3. 1 INTRODUCTION

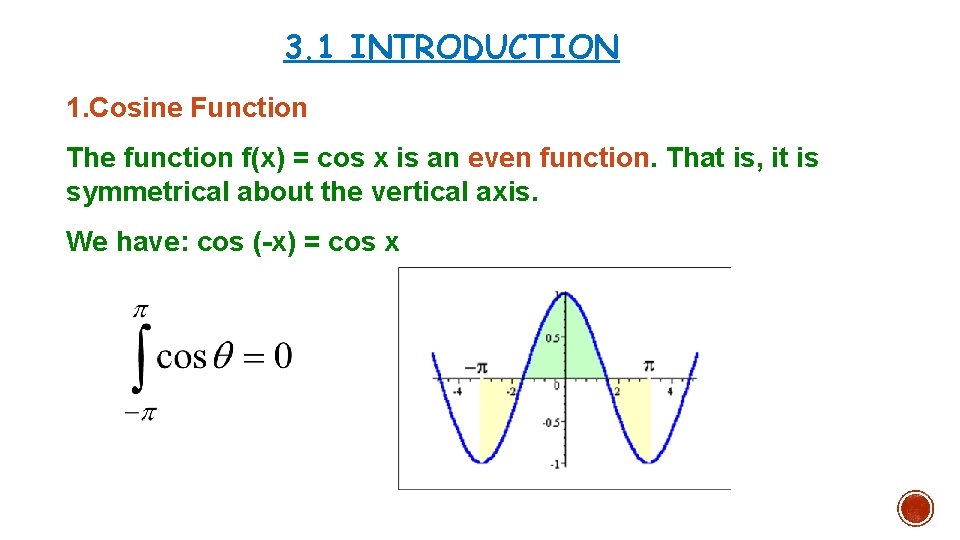
3. 1 INTRODUCTION 1. Cosine Function The function f(x) = cos x is an even function. That is, it is symmetrical about the vertical axis. We have: cos (-x) = cos x

3. 1 INTRODUCTION 2. Sine Function The function f(x) = sin x is an odd function. That is, it is symmetrical about the origin. We have: sin (-x) = -sin x

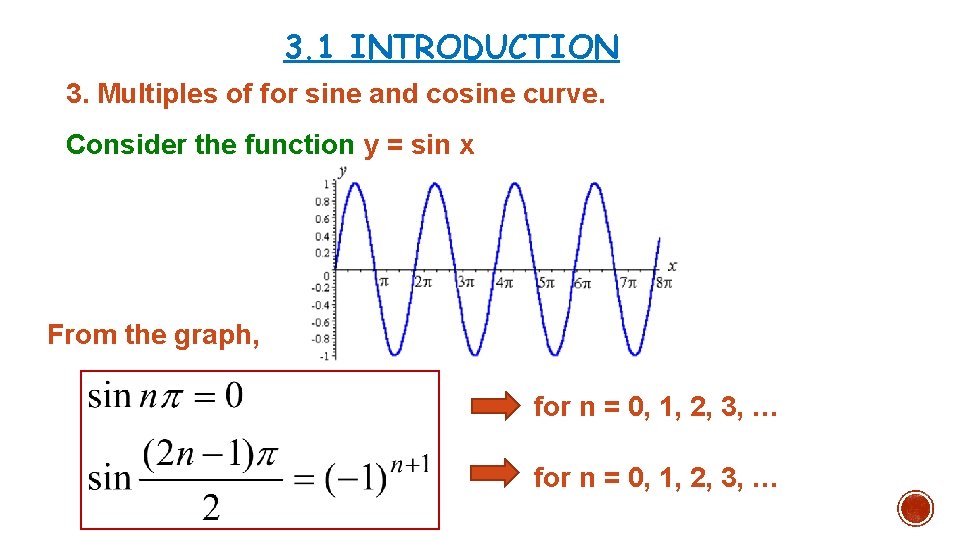
3. 1 INTRODUCTION 3. Multiples of for sine and cosine curve. Consider the function y = sin x From the graph, for n = 0, 1, 2, 3, …

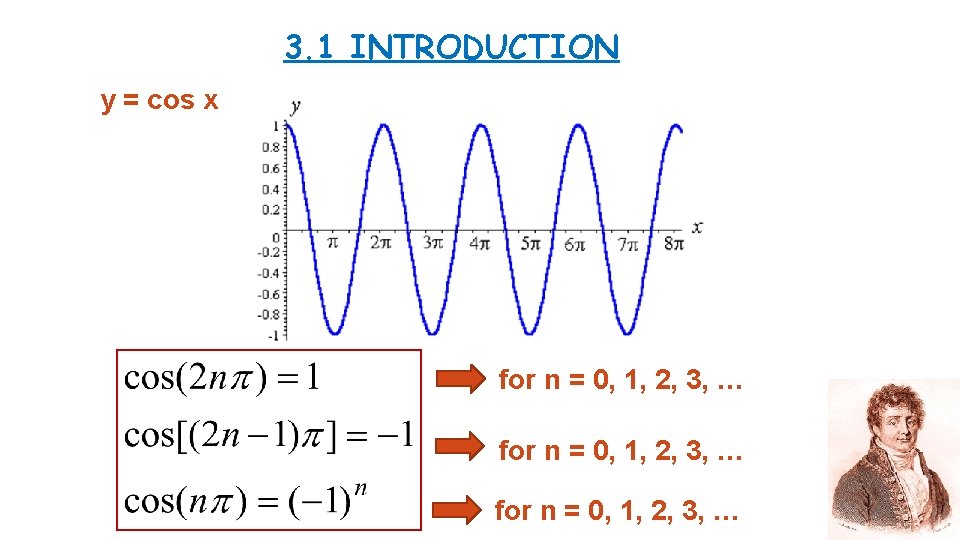
3. 1 INTRODUCTION y = cos x for n = 0, 1, 2, 3, …

3. 2 ORTHOGONAL SET OF FUNCTIONS A set of functions {φ1(x), φ2(x), … } is an orthogonal set of functions on the interval [a, b] if any two functions in the set are orthogonal to each other.

3. 2 ORTHOGONAL SET OF FUNCTIONS Show that: form an orthogonal set on [-π, π].

3. 2 ORTHOGONAL SET OF FUNCTIONS Show that: Solution: is proven!

3. 2 ORTHOGONAL SET OF FUNCTIONS 2 nd Case: Solution:

3. 2 ORTHOGONAL SET OF FUNCTIONS 3 rd Case: Solution:

3. 3 TRIGONOMETRIC FORM OF FOURIER SERIES • A sinusoidal signal, is a periodic signal with period. • The sum of two sinusoids is periodic provided that their frequencies are integral multiples of a fundamental frequency. • We can show that a signal x(t), a sum of sine and cosine functions whose frequencies are integral multiples of, is periodic signal. • Let the signal be

PERIODIC FUNCTIONS A function is periodic if it is defined for all real and if there is some positive number, such that .




FOURIER SERIES Let the signal x(t) be: i. e.

FOURIER SERIES For the signal x(t) to be periodic, it must satisfy the condition x(t) = x(t + T) for all t, i. e.

FOURIER SERIES This proves that the signal x(t), which is summation of sine and cosine functions of frequencies 0, ω0, 2ω0, …, kω0 is a periodic signal x(t) with period T.

FOURIER SERIES The infinite series of sine and cosine terms of frequencies 0, ω0, 2ω0, …, kω0 is known as trigonometric form of Fourier series and can be written as: or (1) The constants a 0, a 1, …, an, b 0, b 1, …, bn, are called Fourier coefficients.

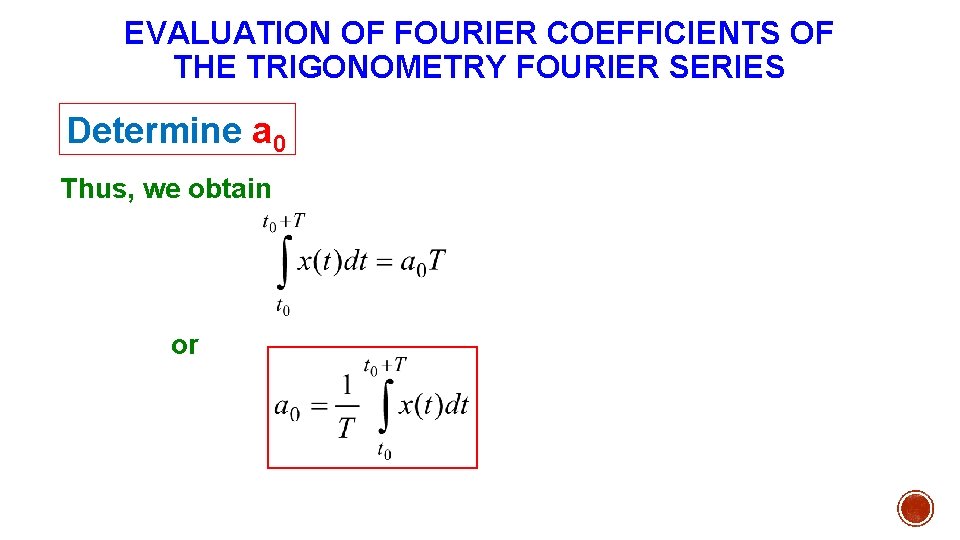
EVALUATION OF FOURIER COEFFICIENTS OF THE TRIGONOMETRY FOURIER SERIES Determine a 0 Integrate both sides of (1) over one period (t 0 to t 0 + T)

EVALUATION OF FOURIER COEFFICIENTS OF THE TRIGONOMETRY FOURIER SERIES Determine a 0 We know that and since the net areas of sinusoids over complete periods are zero for any nonzero integer n and any time t 0.

EVALUATION OF FOURIER COEFFICIENTS OF THE TRIGONOMETRY FOURIER SERIES Determine a 0 Thus, we obtain or

EVALUATION OF FOURIER COEFFICIENTS OF THE TRIGONOMETRY FOURIER SERIES Determine an, bn We can use the following results: 1. 3. for all m and n 2.

EVALUATION OF FOURIER COEFFICIENTS OF THE TRIGONOMETRY FOURIER SERIES Determine an, bn To find an, multiply the equation (1) by cos mω0 t and integrate over one period. That is,

EVALUATION OF FOURIER COEFFICIENTS OF THE TRIGONOMETRY FOURIER SERIES Determine an, bn To first and third integrals are equal zero and the second integral is equal to T/2 when m = n. 0 0

EVALUATION OF FOURIER COEFFICIENTS OF THE TRIGONOMETRY FOURIER SERIES Therefore, or

EVALUATION OF FOURIER COEFFICIENTS OF THE TRIGONOMETRY FOURIER SERIES To find bn, multiply both sides of equation (1) by sin mω0 t and integrate over one period. Then,

EVALUATION OF FOURIER COEFFICIENTS OF THE TRIGONOMETRY FOURIER SERIES The first and second integrals are zero, and the third integral is equal to T/2 when m = n. Thus, 0 0

EVALUATION OF FOURIER COEFFICIENTS OF THE TRIGONOMETRY FOURIER SERIES Thus, or *a 0, an and bn are called trigonometric Fourier series coefficients.

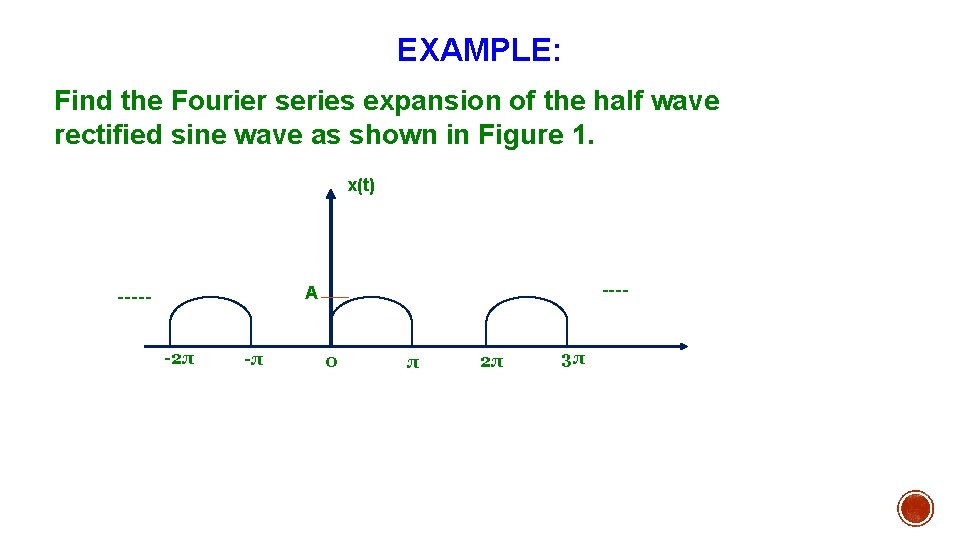
EXAMPLE: Find the Fourier series expansion of the half wave rectified sine wave as shown in Figure 1. x(t) ---- A -----2π -π 0 π 2π 3π

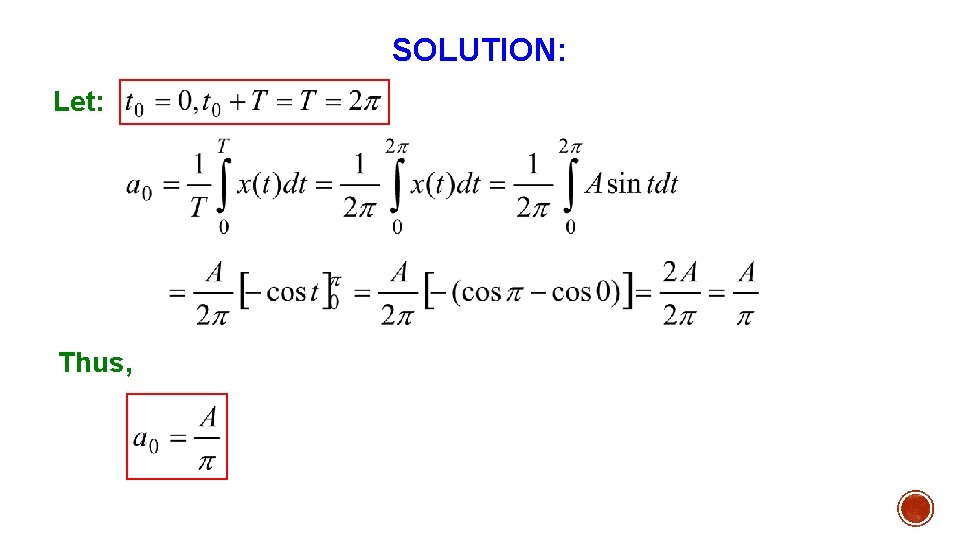
SOLUTION: The periodic waveform shown in Figure with period 2 π is half of a sine wave with period 2π. Now the fundamental period: T = 2π. Fundamental frequency:

SOLUTION: Let: Thus,

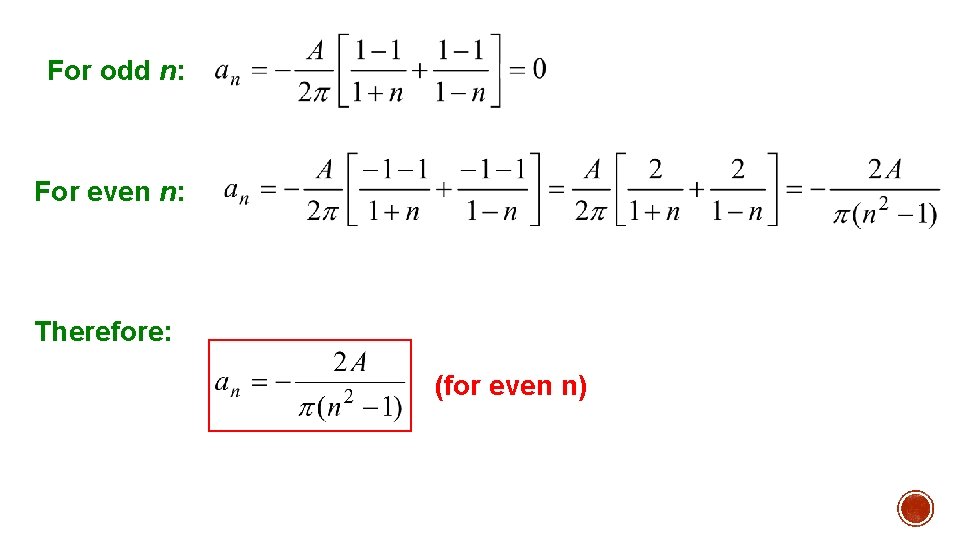
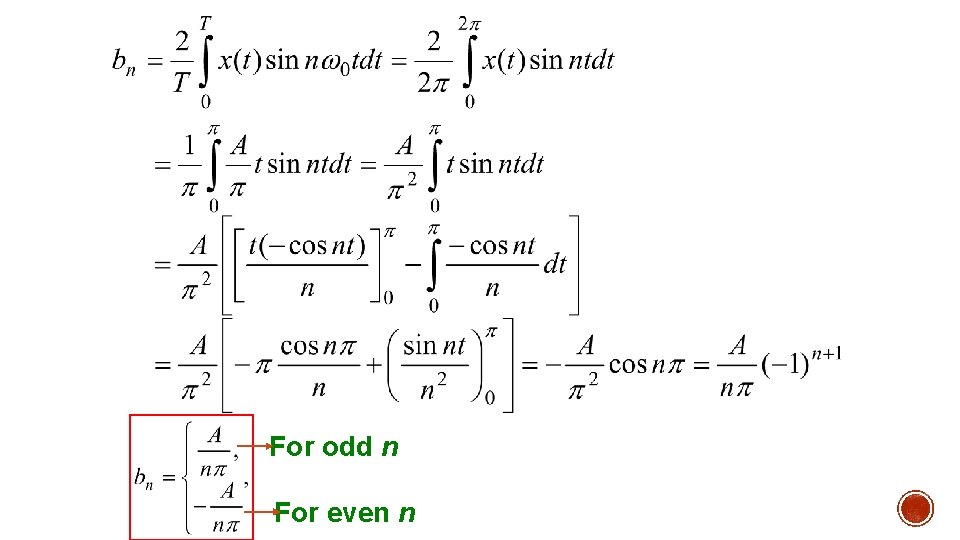
For odd n: For even n: Therefore: (for even n)
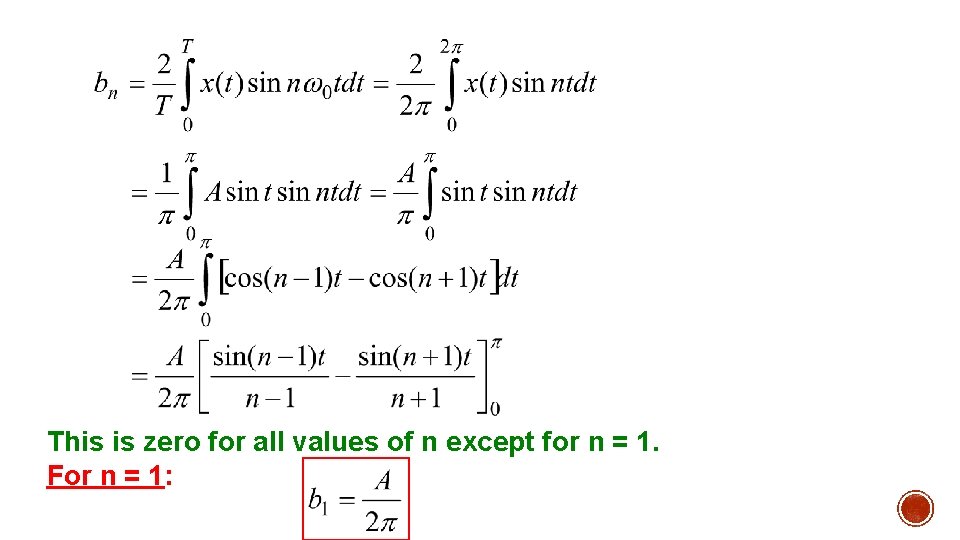
This is zero for all values of n except for n = 1. For n = 1:

Therefore, the trigonometric Fourier series is:

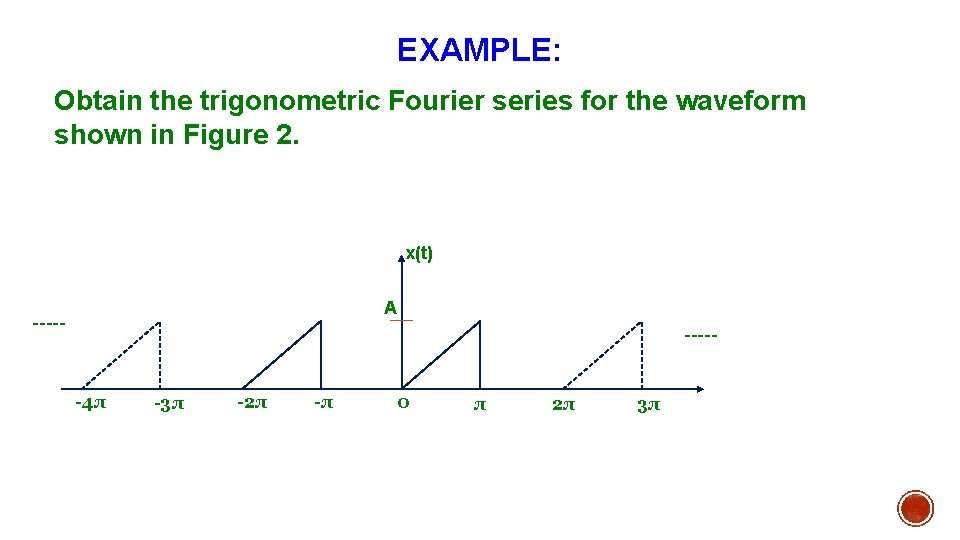
EXAMPLE: Obtain the trigonometric Fourier series for the waveform shown in Figure 2. x(t) A ----- -4π -3π -2π -π 0 π 2π 3π

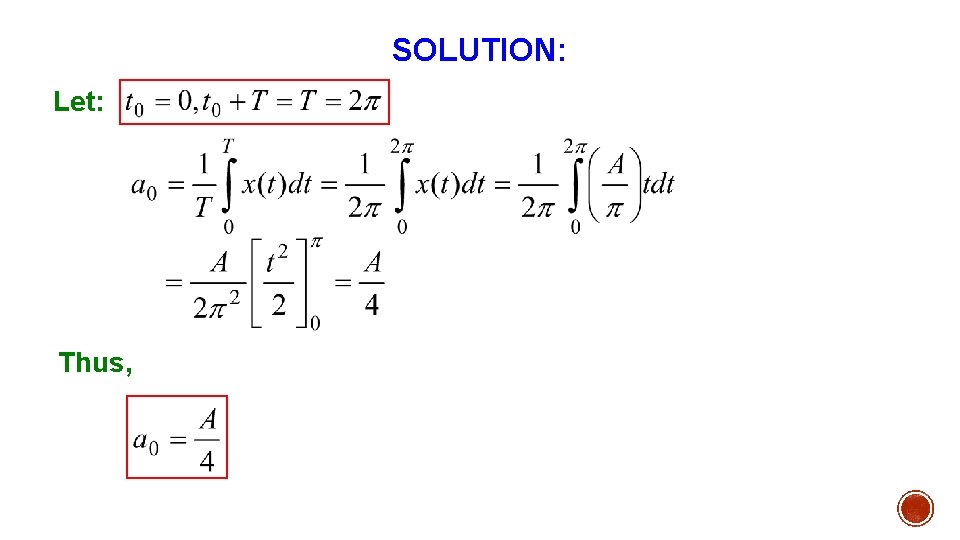
SOLUTION: The waveform shown in Figure is periodic with a period T = 2π. Let: Then, Fundamental frequency: The waveform is described by:

SOLUTION: Let: Thus,
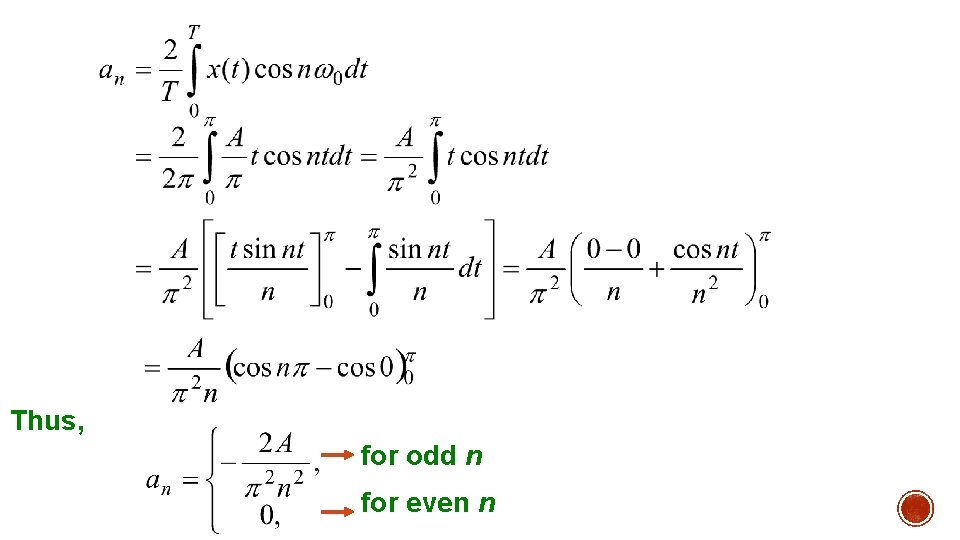
Thus, for odd n for even n

For odd n For even n

The trigonometric Fourier series is:

EXPONENTIAL FOURIER SERIES COMPLEX EXPONENTIALS

EXPONENTIAL FOURIER SERIES The set of complex exponential functions: Forms a closed orthogonal set over an interval (t 0, t 0 + T) where T=(2π/ω0) for any value of t 0, and therefore it can be used as a Fourier series. Using Euler’ identity, we can write:

Substituting this in the definition of cosine Fourier representation, we obtain:

Letting n = -k in the second summation, we have On comparing the above equations for x(t), we get n>0 k<0

Let us define Thus i. e This is known as exponential form of Fourier series. The above equation is called the synthesis equation.

So the exponential series from cosine series is:

DETERMINATION OF THE COEFFICIENTS OF EXPONENTIAL FOURIER SERIES We have: Multiplying both sides by and integrating over one period,

We know Thus, or or Where Cn are the Fourier coefficients of the exponential series.

q The Fourier coefficients of x(t) have only a discrete spectrum because values of Cn exist only for discrete values of n. q As it represents a complex spectrum, it has both magnitude and phase spectra. q Noted: a. The magnitude line spectrum is always an even function of n b. The phase line spectrum is always an odd function of n.

TRIGONOMETRIC FOURIES SERIES FROM EXPONENTIAL FOURIER SERIES The complex exponential Fourier series is given by:

TRIGONOMETRIC FOURIES SERIES FROM EXPONENTIAL FOURIER SERIES Comparing with standard trigonometric Fourier series: We get conversion of exponential to Trigonometric

EXPONENTIAL FOURIER SERIES FROM TRIGONOMETRIC FOURIES SERIES From exponential series, we know:

EXPONENTIAL FOURIER SERIES FROM TRIGONOMETRIC FOURIES SERIES We get conversion of trigonometric to exponential FS:

COSINE FOURIER SERIES FROM EXPONENTIAL FOURIER SERIES We know that:

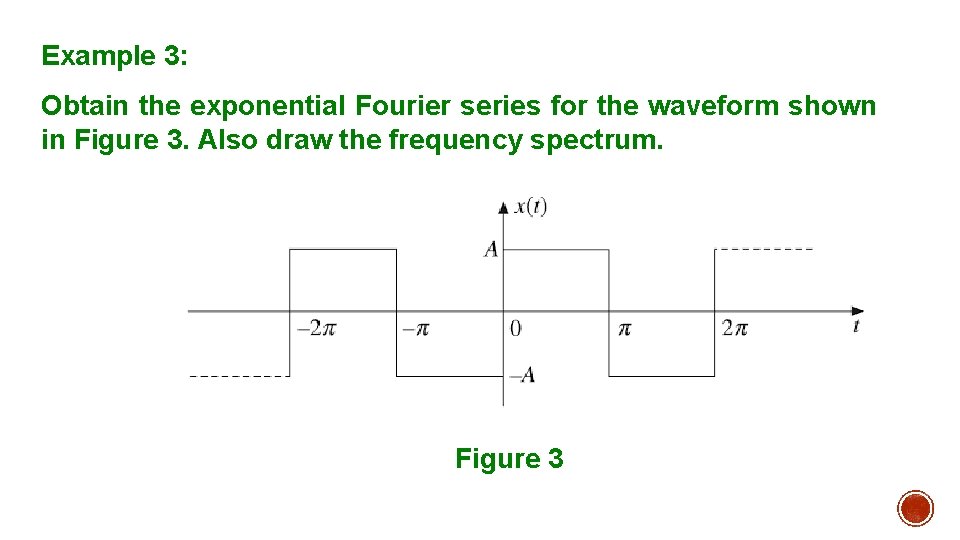
Example 3: Obtain the exponential Fourier series for the waveform shown in Figure 3. Also draw the frequency spectrum. Figure 3

Solution: The periodic waveform shown in Figure 3 with a period T = 2π can be expressed as: Let And fundamental frequency:

Solution: Exponential Fourier Series:
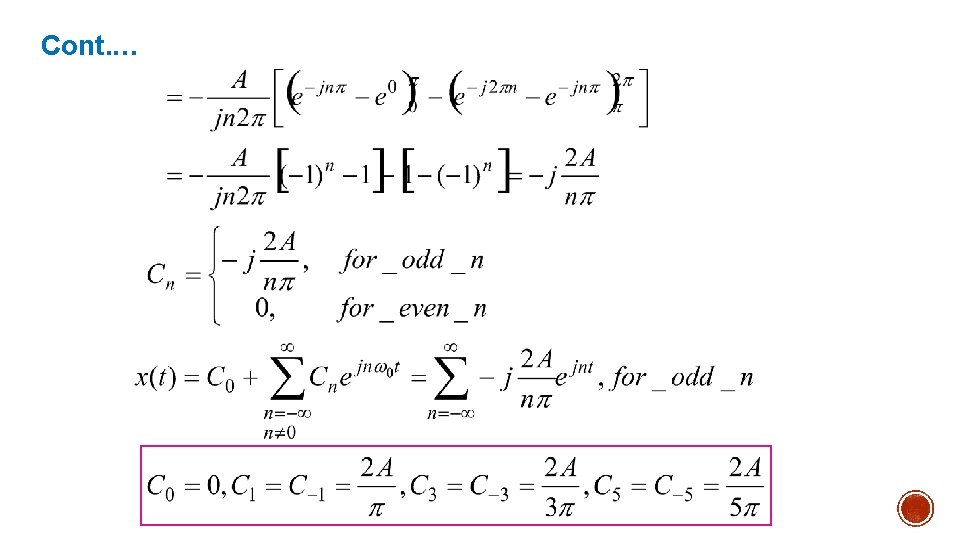
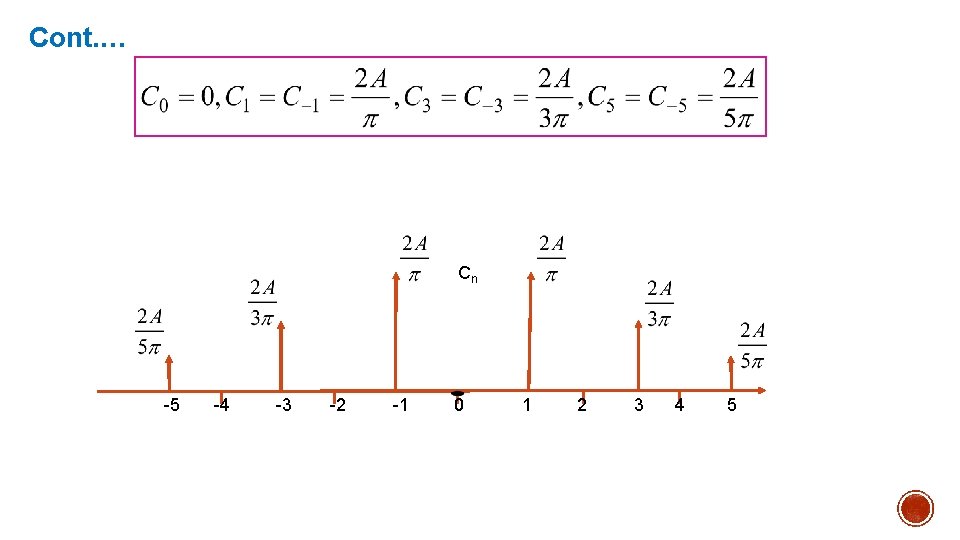
Cont. …

Cont. … Cn -5 -4 -3 -2 -1 0 1 2 3 4 5

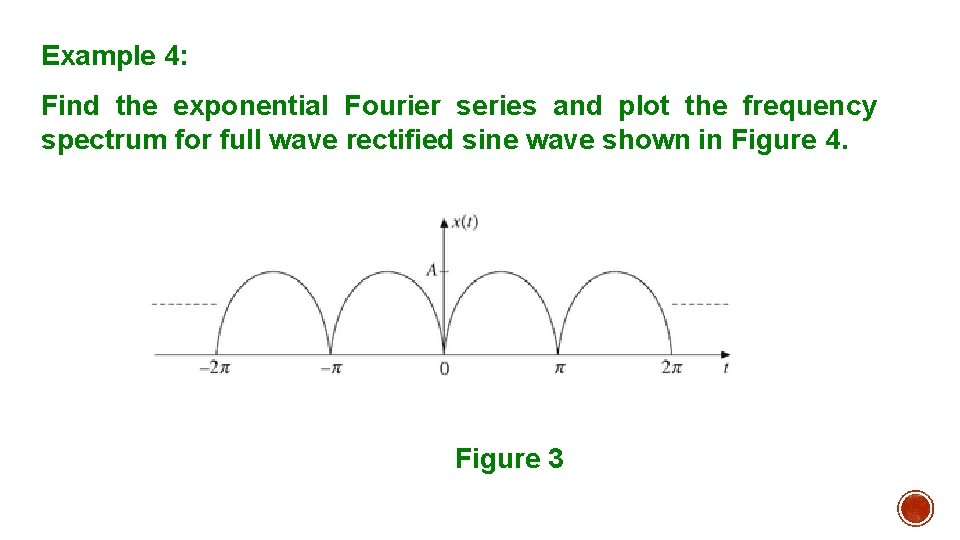
Example 4: Find the exponential Fourier series and plot the frequency spectrum for full wave rectified sine wave shown in Figure 4. Figure 3

Solution: The waveform shown in Figure 4 can be expressed over one period (0 to π) as: where Because it is part of a sine wave with period = 2 π. The full wave rectified sine wave is periodic with T = π.

Exponential Fourier Series:

Cont. …

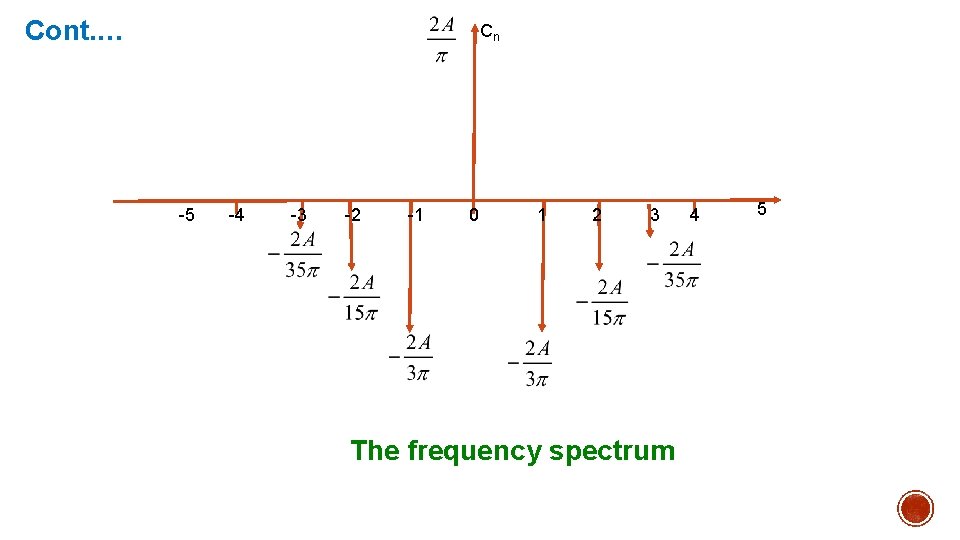
Cont. … Cn -5 -4 -3 -2 -1 0 1 2 3 The frequency spectrum 4 5

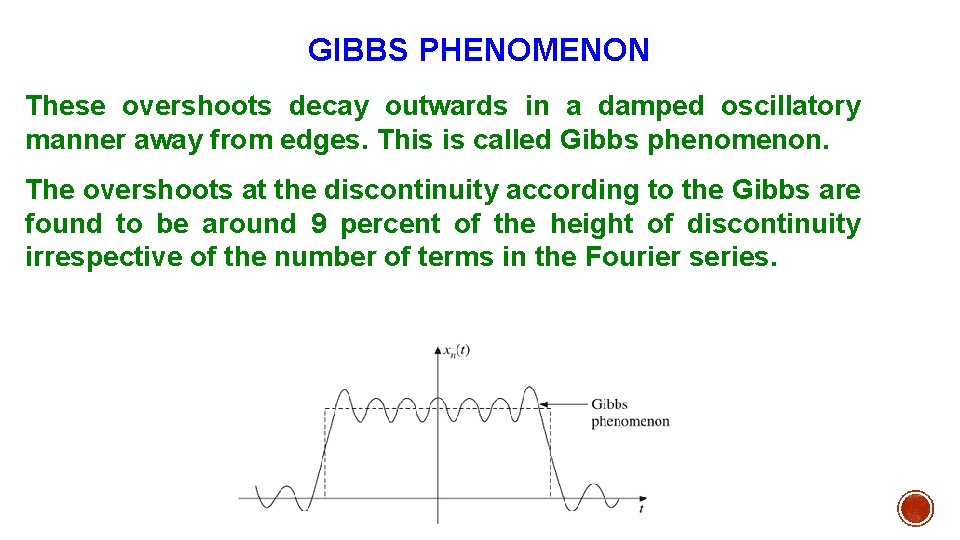
GIBBS PHENOMENON Gibbs discovered that for a periodic signal with discontinuities, if the signal is reconstructed by adding the Fourier series, overshoots appear around the edges.

GIBBS PHENOMENON These overshoots decay outwards in a damped oscillatory manner away from edges. This is called Gibbs phenomenon. The overshoots at the discontinuity according to the Gibbs are found to be around 9 percent of the height of discontinuity irrespective of the number of terms in the Fourier series.

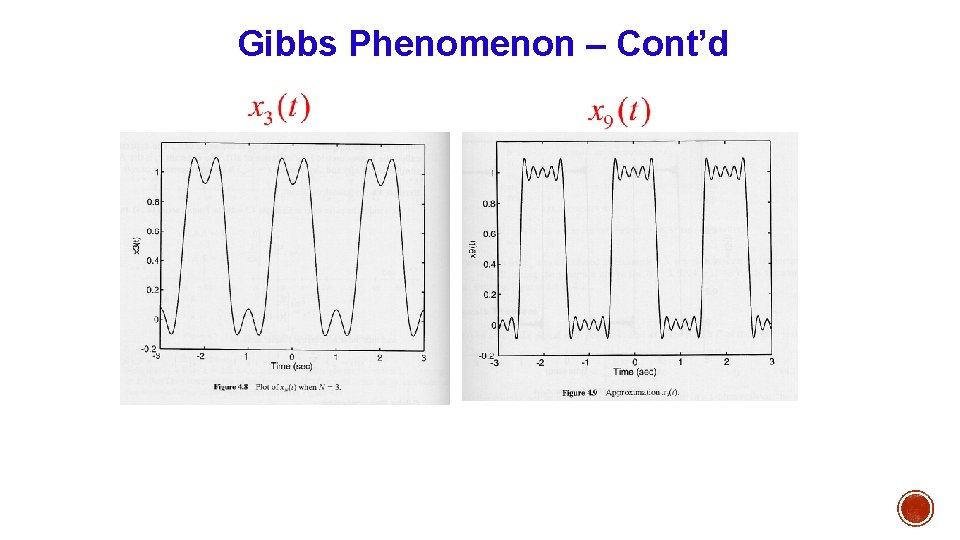
GIBBS PHENOMENON q It has also been observed that as more number of terms in the series are added, the frequency increases, overshoots, get sharper, but the adjoining oscillation amplitude reduces. q That is error between the original signal x(t) and the truncated signal xn(t) reduced except at the edges as n increases. q Thus, the truncated Fourier series approaches x(t) as the number of terms in approximation increases.

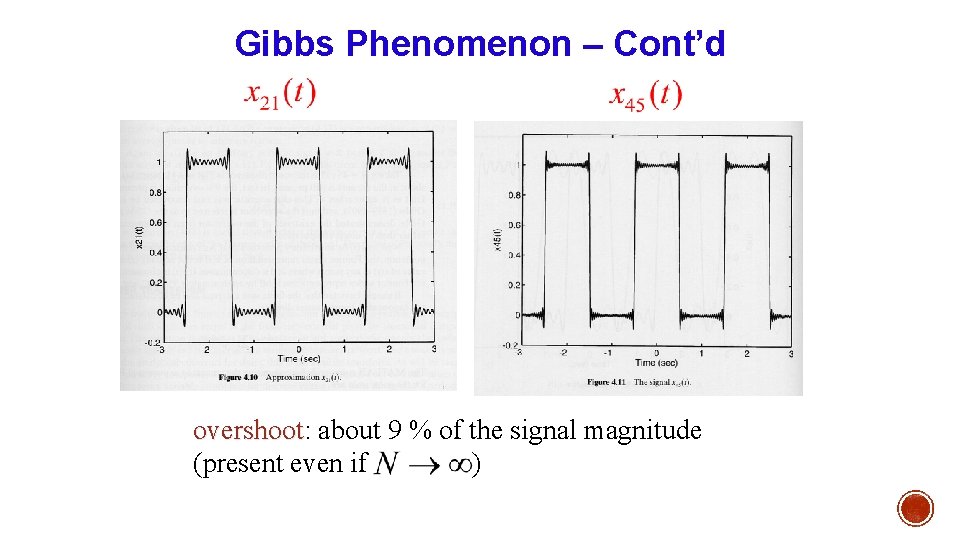
Gibbs Phenomenon – Cont’d

Gibbs Phenomenon – Cont’d overshoot: overshoot about 9 % of the signal magnitude (present even if )

PARSEVAL’S THEOREM If, and, Then, the Parseval’s relation states that, [for complex x 1(t) and x 2(t)] And, Parseval’s identity states that,

PARSEVAL’S THEOREM Proof: Parseval’s relation, Interchanging the order of integration and summation in the RHS,

PARSEVAL’S THEOREM Therefore, Proved. Parseval’s Identity: If x 1(t)=x 2(t)=x(t), then the relation changes to

PARSEVAL’S THEOREM Since, Substitute this value, Proved.

REFERENCES § A. Anand Kumar, “Signals & Systems”, PHI Learning Private Limited. 2 nd edition. New Delhi. § Simon Haykin and Barry Van Veen, “Signals and Systems”, Wiley, 2 nd Edition, 2002 § M. J. Roberts, “Signals and Systems”, International Edition, Mc. Graw Hill, 2 nd Edition 2012
 Convert trigonometric fourier series to exponential
Convert trigonometric fourier series to exponential Communicative signals and informative signals
Communicative signals and informative signals Arbitrariness in human language and animal language
Arbitrariness in human language and animal language Communicative and informative signals
Communicative and informative signals Fourier transform of multiplication of two signals
Fourier transform of multiplication of two signals Fourier transform of multiplication of two signals
Fourier transform of multiplication of two signals Fourier analysis of discrete time signals
Fourier analysis of discrete time signals Discrete time fourier series
Discrete time fourier series Signals and systems oppenheim solutions chapter 5
Signals and systems oppenheim solutions chapter 5 Coral phone system
Coral phone system Cs 281 wordpress
Cs 281 wordpress Cpr e 281
Cpr e 281 It is a circular or elliptical anticlinal structure
It is a circular or elliptical anticlinal structure Weathering types
Weathering types 2812840027
2812840027 Cs 281
Cs 281 49 numeros romanos
49 numeros romanos Stoytchev 281
Stoytchev 281 Stoytchev 281
Stoytchev 281 18 gelecek aylara ait giderler ve gelir tahakkukları
18 gelecek aylara ait giderler ve gelir tahakkukları Dönem ayirici hesaplar 180 181 280 281 380 381
Dönem ayirici hesaplar 180 181 280 281 380 381 Series de fourier
Series de fourier Formulas de fourier
Formulas de fourier Serie de fourier compleja
Serie de fourier compleja Time domain and frequency domain
Time domain and frequency domain Linear property of fourier transform
Linear property of fourier transform Half range fourier cosine series
Half range fourier cosine series Fourier series of periodic function
Fourier series of periodic function Wave symmetry
Wave symmetry Use of fourier series
Use of fourier series Fourier series multiplication property
Fourier series multiplication property Rectified sine wave fourier series
Rectified sine wave fourier series Series de fourier
Series de fourier Polar fourier series
Polar fourier series Orthogonal functions in fourier series
Orthogonal functions in fourier series Fourier series multiplication property
Fourier series multiplication property Fourier series
Fourier series Site:slidetodoc.com
Site:slidetodoc.com Fourier transform
Fourier transform Medical imaging
Medical imaging Inverse fourier transform
Inverse fourier transform Fourier's theorem
Fourier's theorem Half range fourier series
Half range fourier series Discrete time fourier series
Discrete time fourier series What is dft
What is dft Fourier series circuit analysis
Fourier series circuit analysis Fourier series and integrals
Fourier series and integrals Dirac fourier transform
Dirac fourier transform Series complejas de fourier
Series complejas de fourier Matlab fourier series coefficients
Matlab fourier series coefficients Series fourier
Series fourier Fourier sine series
Fourier sine series Series de fourier
Series de fourier Parseval's theorem in signals and systems
Parseval's theorem in signals and systems Fourier series
Fourier series Series de fourier
Series de fourier Series de fourier
Series de fourier Orthogonal functions in fourier series
Orthogonal functions in fourier series Fourier
Fourier Fourier series
Fourier series Wolfram fourier series
Wolfram fourier series Define fourier series
Define fourier series Pulse train fourier transform
Pulse train fourier transform Fourier series of unit step function
Fourier series of unit step function Fourier series formula
Fourier series formula Transformata fourier
Transformata fourier Fourier transform in polar coordinates
Fourier transform in polar coordinates Fourier series
Fourier series Fourier series of periodic function
Fourier series of periodic function Ac to dc half wave rectifier
Ac to dc half wave rectifier Fourier series and orthogonal functions
Fourier series and orthogonal functions Signals
Signals Precedence rule in signals and systems
Precedence rule in signals and systems Convolution sum in signals and systems
Convolution sum in signals and systems Convolution sum and convolution integral
Convolution sum and convolution integral Introduction to signals and systems
Introduction to signals and systems Convolution sum in signals and systems
Convolution sum in signals and systems Sinusoidal signal
Sinusoidal signal Signals and systems
Signals and systems