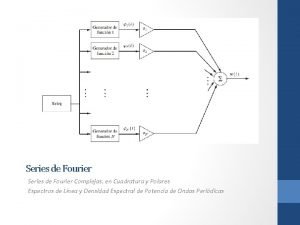
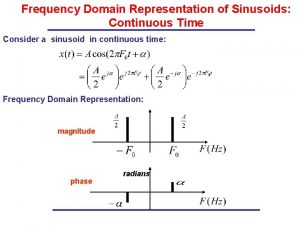
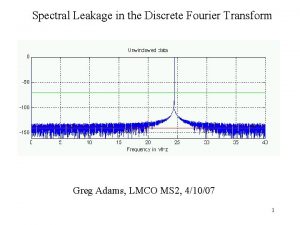
Chapter 4 Fourier Series 1 TOPIC Fourier series



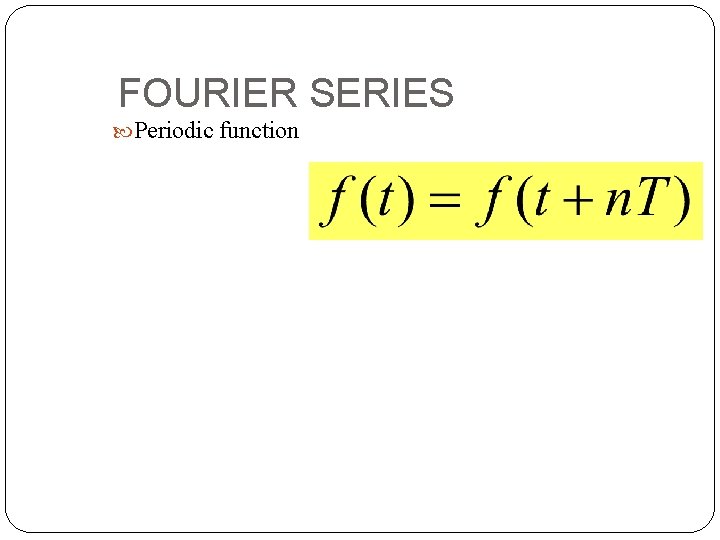
















































- Slides: 71

Chapter 4: Fourier Series 1

TOPIC: Fourier series definition Fourier coefficients The effect of symmetry on Fourier series coefficients Alternative trigonometric form of Fourier series Example of Fourier series analysis for RL and RC circuit Average power calculation of periodic function rms value of periodic function Exponential form of Fourier series Amplitude and phase spectrum 2

FOURIER SERIES DEFINITION The Fourier Series of a periodic function f(t) is a representation that resolves f(t) into a DC component and an AC component comprising an infinite series of harmonic sinusoids. 3
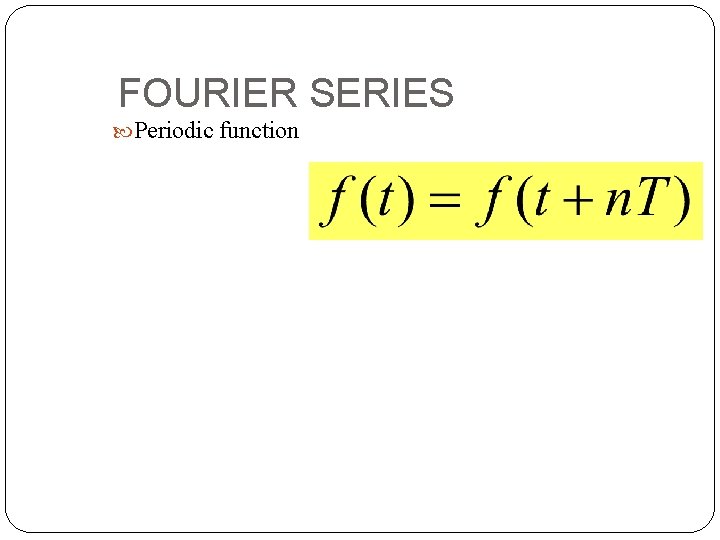
FOURIER SERIES Periodic function 4

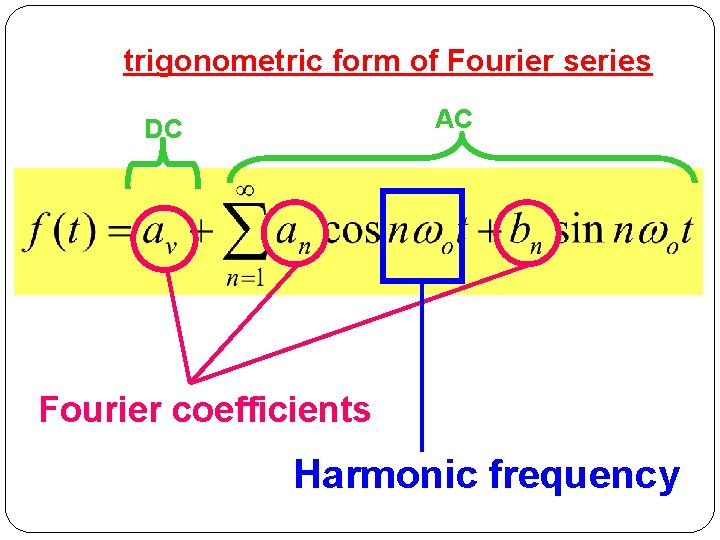
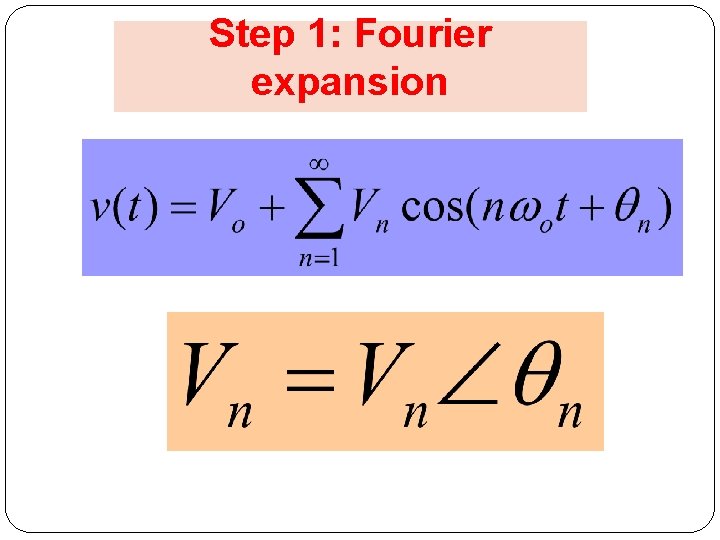
trigonometric form of Fourier series AC DC Fourier coefficients Harmonic frequency 5

Condition of convergent a Fourier series (Dirichlet conditions): 1. F(t) is single-valued 2. F(t) has a finite number of finite discontinuities in any one period 3. F(t) has a finite number of maxima and minima in any one period 4. The intergral 6

Fourier coefficients Integral relationship to get Fourier coefficients 7

av coefficient 8

an coefficient 9

bn coefficient 10

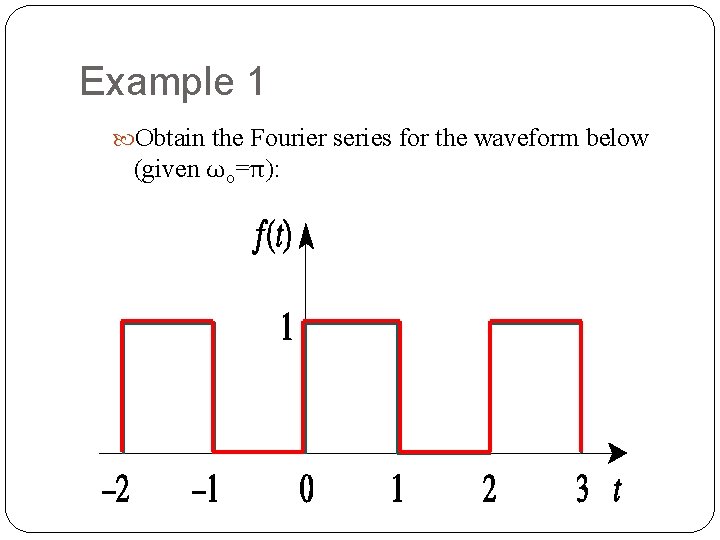
Example 1 Obtain the Fourier series for the waveform below (given ωo=π): 11

Solution: Fourier series: 12

Waveform equation: 13

av coefficient 14

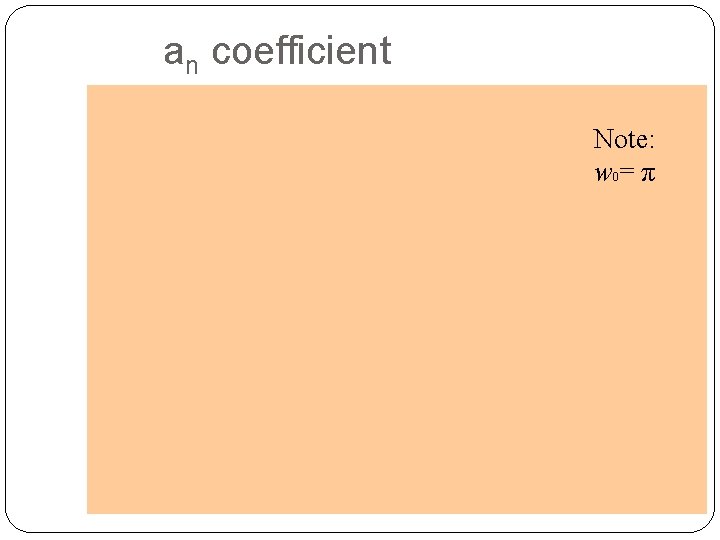
an coefficient Note: w 0= π 15

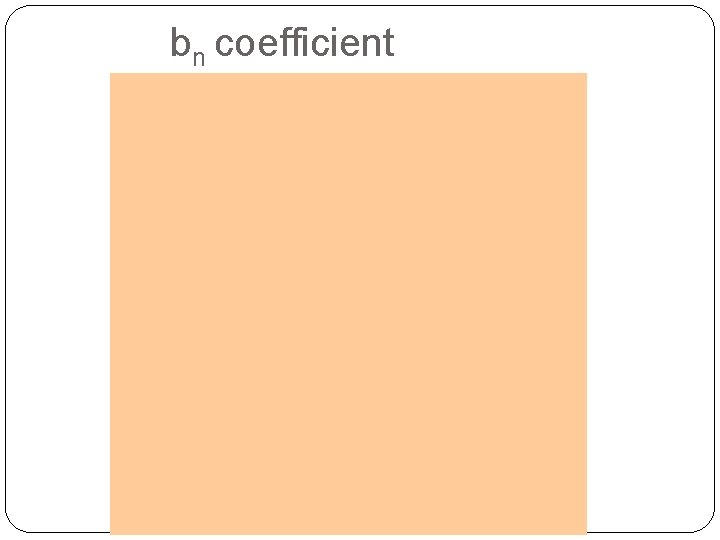
bn coefficient 16

Fit in the coefficients into Fourier series equation: 17

By using n=integer…. 18

THE EFFECT OF SYMMETRY ON FOURIER COEFFICIENTS Even symmetry Odd symmetry Half-wave symmetry Quarter-wave symmetry 19

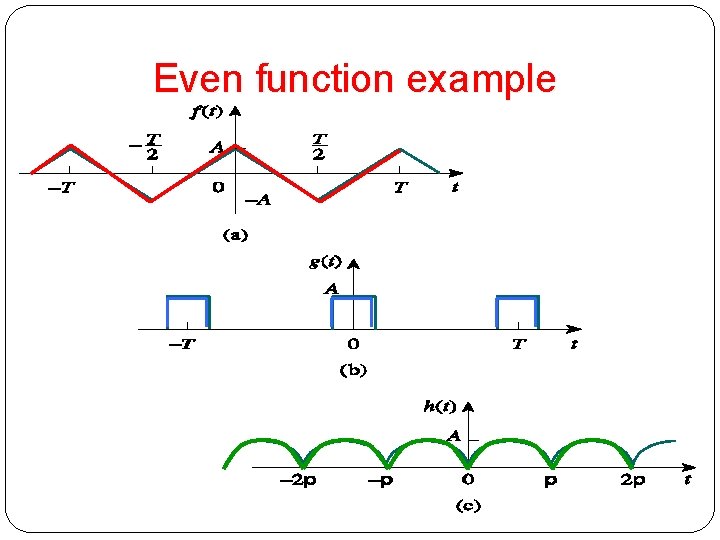
Even Symmetry A function is define as even if 20

Even function example 21

Even function property: 22

Fourier coefficients 23

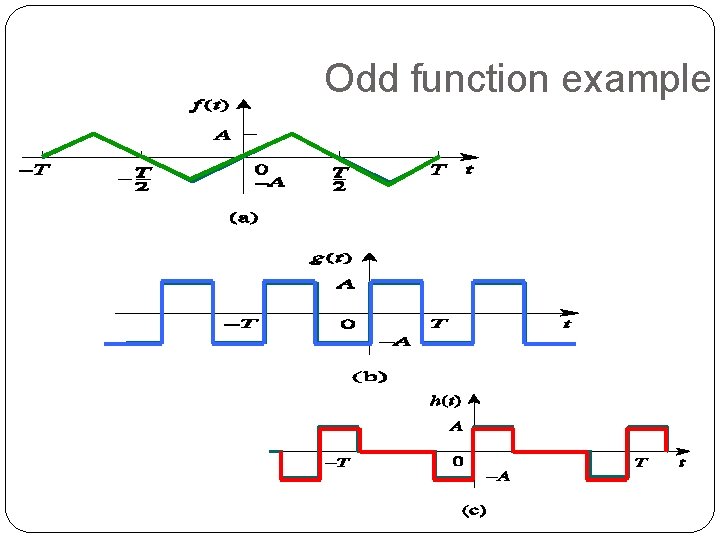
Odd Symmetry A function is define as odd if 24

Odd function example 25

Odd function property: 26

Fourier coefficients 27

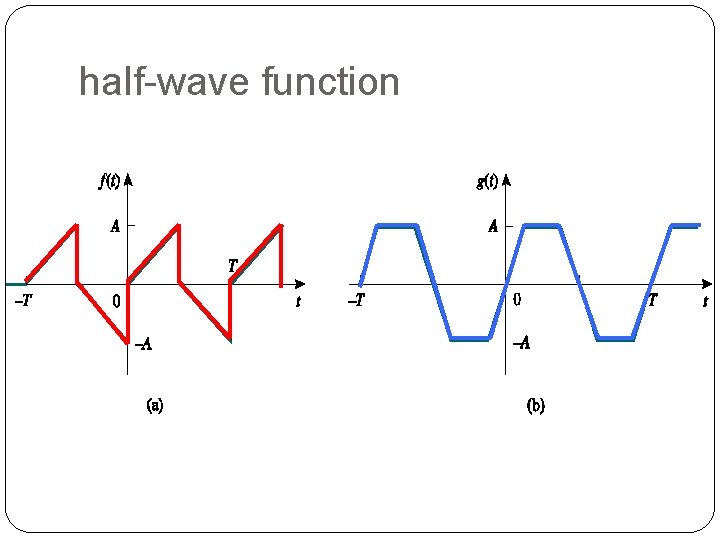
Half-wave symmetry half-wave function: 28

half-wave function 29

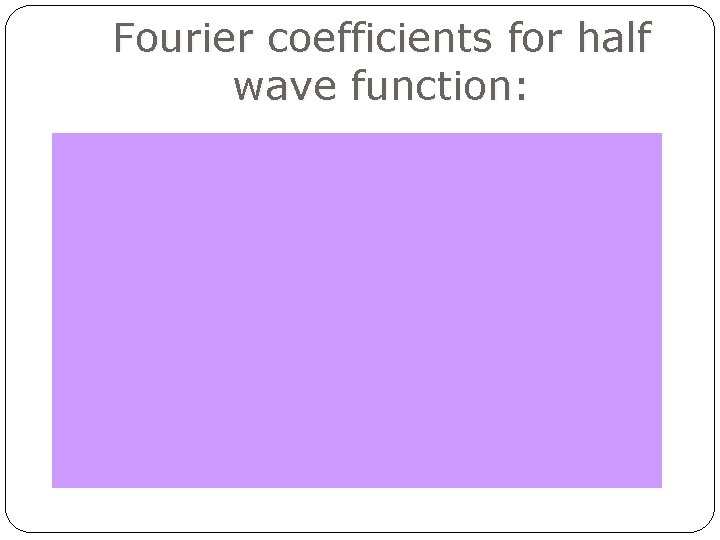
Fourier coefficients for half wave function: 30

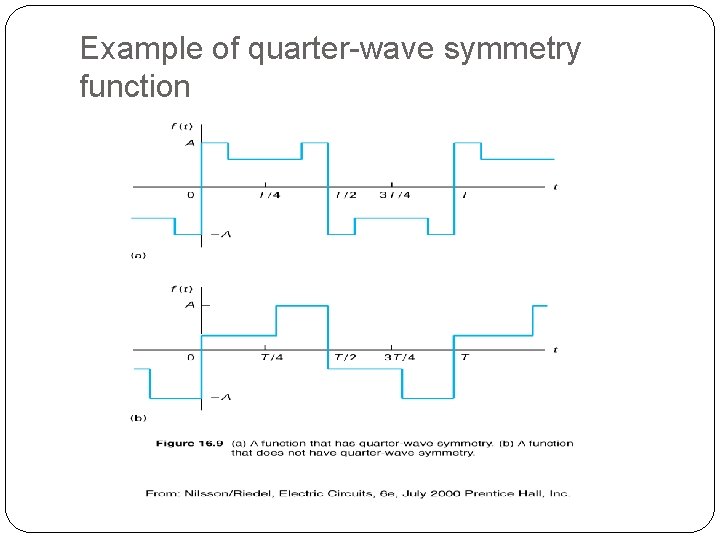
Quarter-wave symmetry A periodic function that has half-wave symmetry and, in addition, symmetry about the mid-point of the positive and negative half-cycles. 31

Example of quarter-wave symmetry function 32

Even quarter-wave symmetry 33

Odd quarter-wave symmetry 34

ALTERNATIVE TRIGONOMETRIC FORM OF THE FOURIER SERIES Fourier series • Alternative form 35

Trigonometric identity • Fourier series 36

Fourier coefficients 37

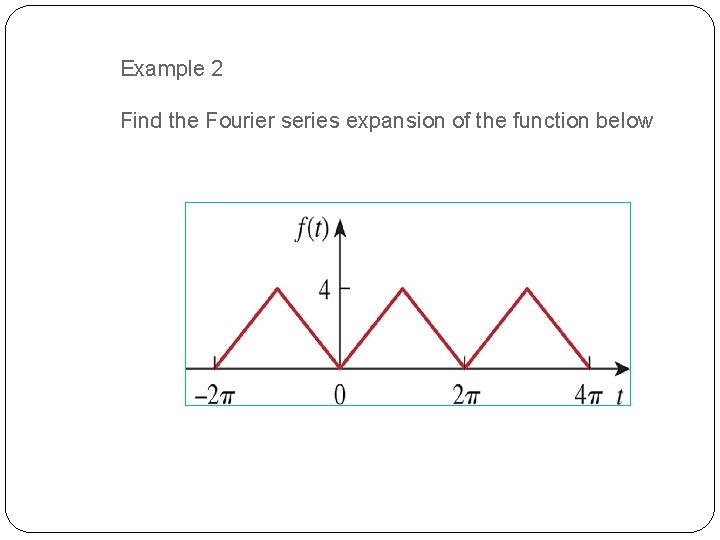
Example 2 Find the Fourier series expansion of the function below 38

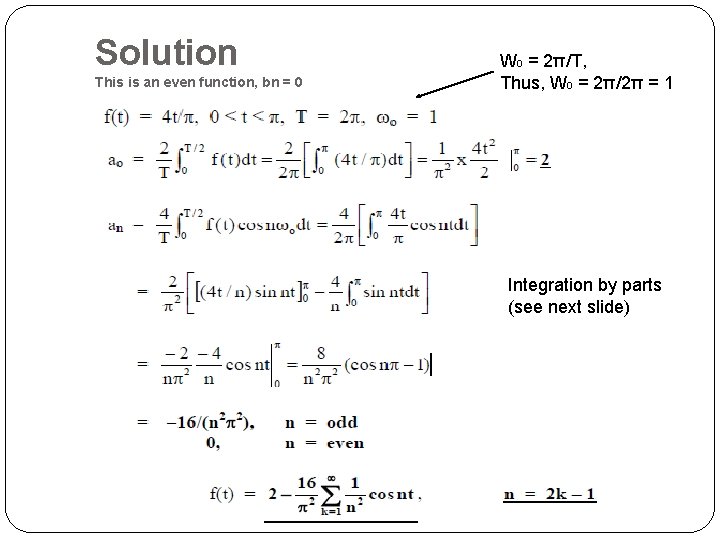
Solution This is an even function, bn = 0 W 0 = 2π/T, Thus, W 0 = 2π/2π = 1 Integration by parts (see next slide) 39

Integration by parts (revision) 40

Example 3 Obtain the trigonometric Fourier series for the waveform shown below:

Solution Integration by parts 42

Example 4 Determine the Fourier series expansion of the function below:

Solution: The function is half wave symmetry

Fourier coefficients for half wave function:

An coefficient:

Bn coefficient:

Fourier series:

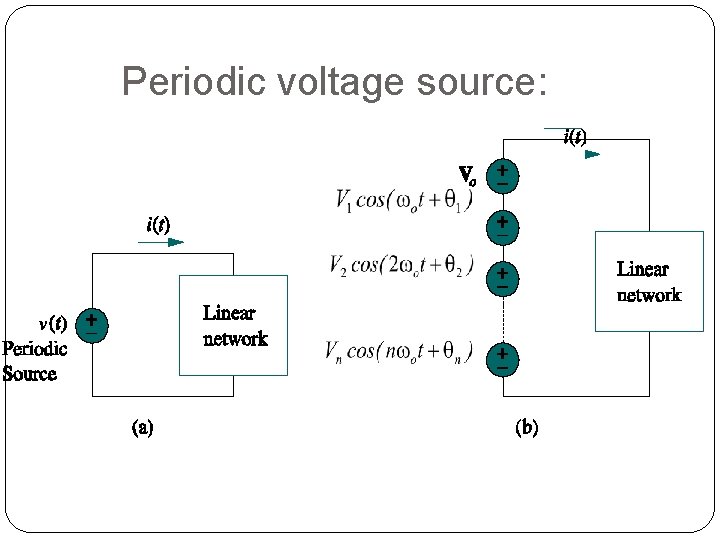
Steps for applying Fourier series: Express the excitation as a Fourier Series Find the response of each term in Fourier Series Add the individual response using the superposition principle 49

Periodic voltage source: 50

Step 1: Fourier expansion 51

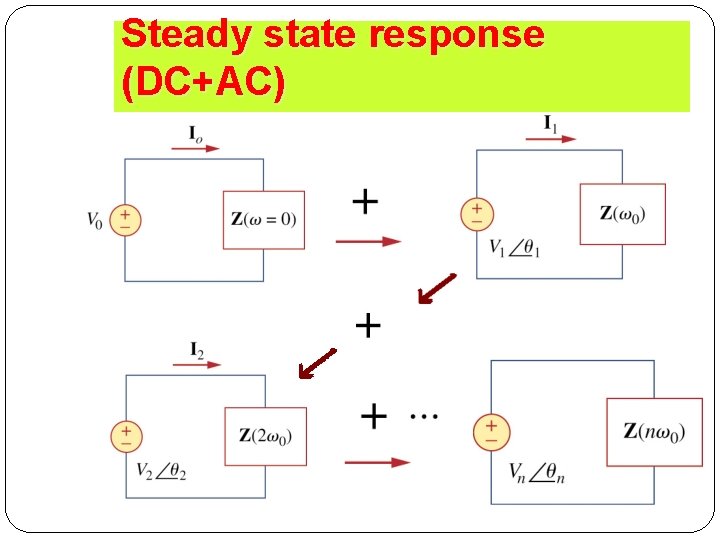
Step 2: find response DC component: set n=0 or ω=0 Time domain: inductor = short circuit capacitor = open circuit 52

Steady state response (DC+AC) 53

Step 3: superposition principle 54

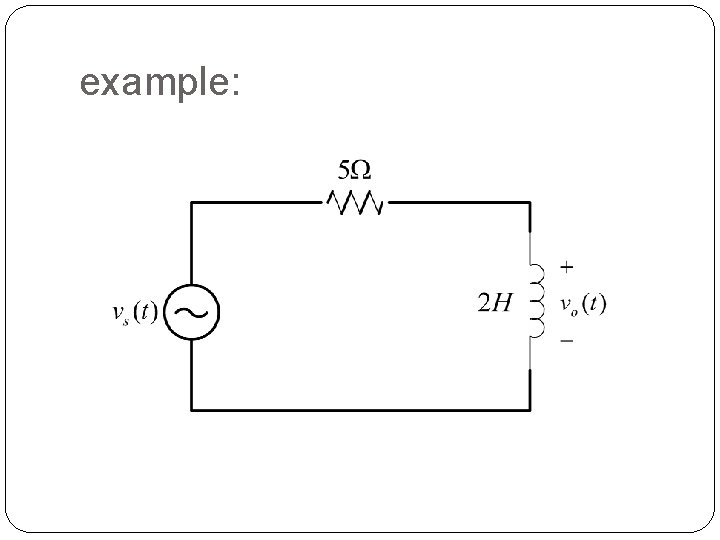
example: 55

Question: If Obtain the response of vo(t) for the circuit using ωn=nωo. 56

Solution: Using voltage divider: Note: L= 2 H R= 5Ω 57

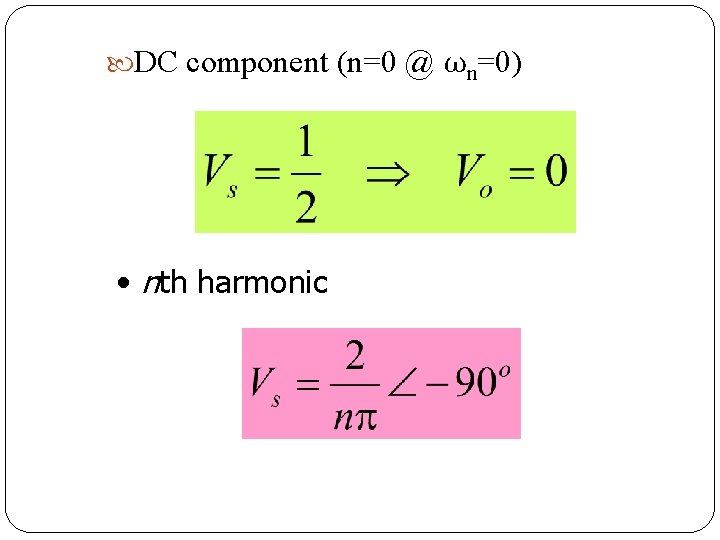
DC component (n=0 @ ωn=0) • nth harmonic 58

Response of vo: Change V 0 into polar form and perform summation at the denominator; Vs 59

In time domain: 60

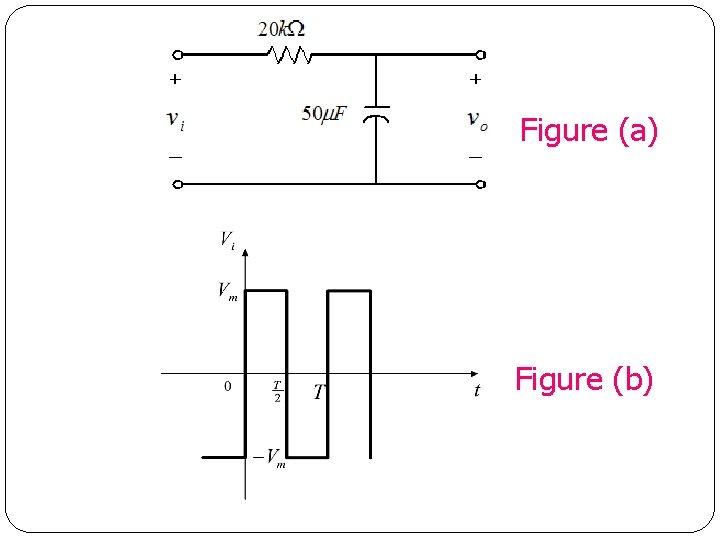
Example of symmetry effect on Fourier coefficients (past year): A square voltage waveform, vi (t) ( as in Fig (b)) Is applied to a circuit as in Fig. (a). If Vm = 60π V and the period is T = 2π s, a) Obtain the Fourier Series for vi (t). b) Obtain the first three nonzero term for vo (t). 61

Figure (a) Figure (b) 62

Solution (a): Response is the Odd Quarter-wave symmetry… 63

Equation of vi (t) for 0<t< T/4: Harmonic frequency: 64

bn coefficient: 65

Fourier series for vi(t): 66

Solution (b): Voltage vi for first three harmonic: 67

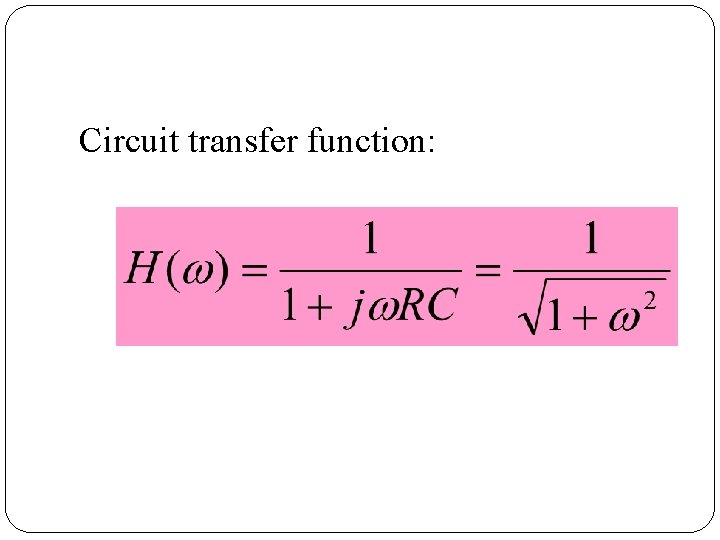
Circuit transfer function: 68

Transfer function for first three harmonic: 69

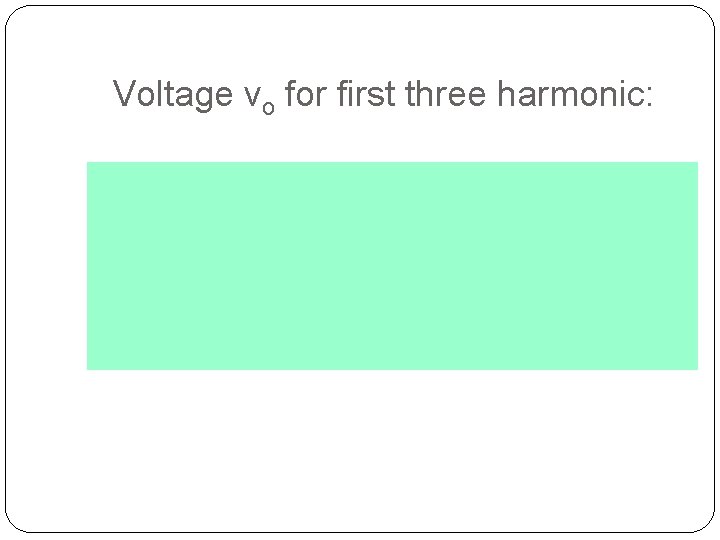
Voltage vo for first three harmonic: 70

First three nonzero term: 71
 Painted paragraph strategy
Painted paragraph strategy Narrow down topic
Narrow down topic Parseval's identity for fourier transform
Parseval's identity for fourier transform Serie de fourier del seno
Serie de fourier del seno Formula series de fourier
Formula series de fourier Serie de fourier
Serie de fourier Frequency domain to time domain
Frequency domain to time domain Fourier transform equations
Fourier transform equations Half range fourier sine series formula
Half range fourier sine series formula Periodic function fourier transform
Periodic function fourier transform Odd quarter wave symmetry
Odd quarter wave symmetry Use of fourier series
Use of fourier series Impulse train fourier transform
Impulse train fourier transform Rectified sine wave fourier series
Rectified sine wave fourier series Fourier transform formula
Fourier transform formula Fourier transform of multiplication of two signals
Fourier transform of multiplication of two signals Bn formula in fourier series
Bn formula in fourier series Polar fourier series
Polar fourier series Orthogonality fourier series
Orthogonality fourier series Fourier series multiplication property
Fourier series multiplication property Fourier series representation of periodic function
Fourier series representation of periodic function Fourier series half range
Fourier series half range Properties of fourier transform
Properties of fourier transform Fourier transform
Fourier transform Fourier
Fourier Fourier's theorem
Fourier's theorem Half range fourier series is defined in
Half range fourier series is defined in Discrete time fourier series
Discrete time fourier series Discrete time fourier series
Discrete time fourier series Discrete time fourier series
Discrete time fourier series Fourier series circuit analysis
Fourier series circuit analysis Fourier series of even and odd functions
Fourier series of even and odd functions Delta function fourier transform
Delta function fourier transform Series complejas de fourier
Series complejas de fourier Matlab fourier series coefficients
Matlab fourier series coefficients Series fourier
Series fourier Orthogonal series expansion
Orthogonal series expansion Series de fourier
Series de fourier Parseval's theorem in signals and systems
Parseval's theorem in signals and systems Fourier series
Fourier series Series de fourier
Series de fourier Series de fourier
Series de fourier Orthogonal functions in fourier series
Orthogonal functions in fourier series Ejercicios resueltos de series de fourier
Ejercicios resueltos de series de fourier Fourier series coefficients formula
Fourier series coefficients formula Wolfram fourier series
Wolfram fourier series Define fourier series of a function
Define fourier series of a function Synthesis equation fourier series
Synthesis equation fourier series Unit impluse
Unit impluse Fourier series formula
Fourier series formula Fourier series
Fourier series Polar fft
Polar fft Fourier series
Fourier series Fourier series of periodic function
Fourier series of periodic function Three phase full wave controlled rectifier with rl load
Three phase full wave controlled rectifier with rl load Fourier series and orthogonal functions
Fourier series and orthogonal functions Maclaurin series vs taylor series
Maclaurin series vs taylor series Balmer series lyman series
Balmer series lyman series Maclaurin series vs taylor series
Maclaurin series vs taylor series Deret maclaurin
Deret maclaurin Ibm p series models
Ibm p series models Shunt feedback amplifier analysis
Shunt feedback amplifier analysis Series aiding and series opposing
Series aiding and series opposing Sum of infinite series
Sum of infinite series Chapter 5 selecting a topic and a purpose
Chapter 5 selecting a topic and a purpose Specific purpose statements
Specific purpose statements Chapter 12 sequences and series answers
Chapter 12 sequences and series answers Chapter 23 series and parallel circuits
Chapter 23 series and parallel circuits Geometric sequence
Geometric sequence Chapter 1 sequences and series
Chapter 1 sequences and series Sequences and series math 20-1
Sequences and series math 20-1 What is a topic sentence
What is a topic sentence