Srie de Fourier As sries trigonomtricas infinitas formadas


![As funções sen [(m x)/T] e cos [(m x)/T], m = 1, 2, . As funções sen [(m x)/T] e cos [(m x)/T], m = 1, 2, .](https://slidetodoc.com/presentation_image_h/1fcc8ccd10388fd6691abdce57800b98/image-3.jpg)
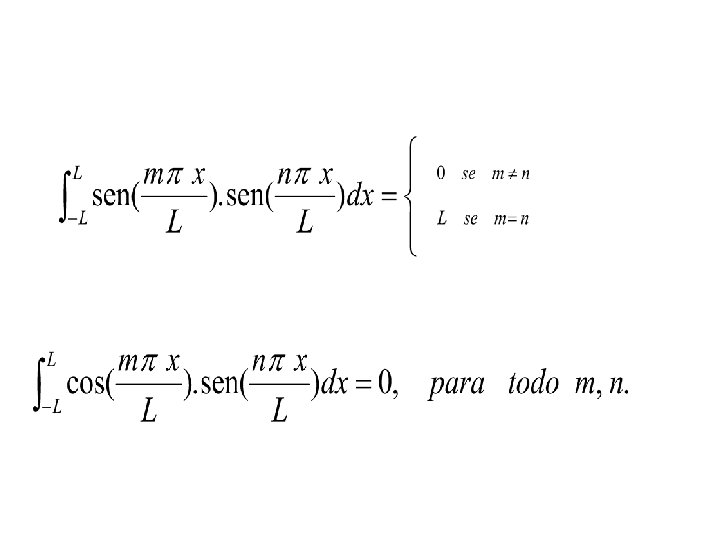


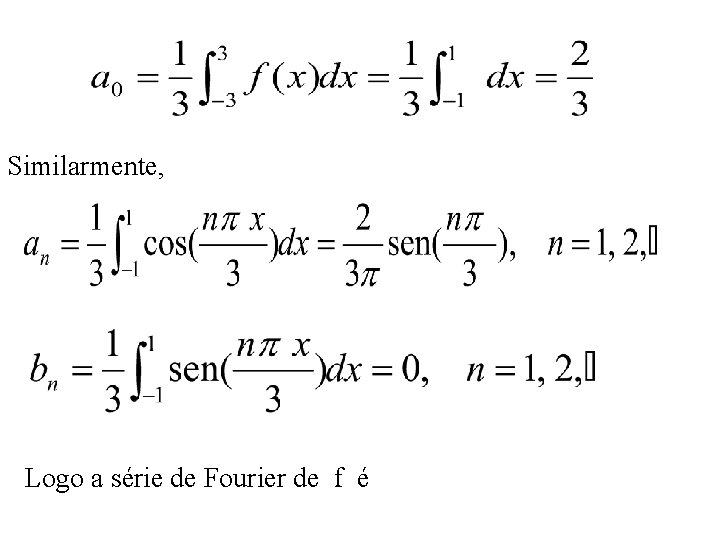








- Slides: 15

Série de Fourier As séries trigonométricas infinitas formadas por seno e/ou coseno são chamadas séries de Fourier. Seja a série na forma No conjunto de pontos onde ela converge, ela define uma função f, cujos valores em cada ponto x é a soma da série para aquele valor de x. Dizemos então que esta série é a série de Fourier de f.

Periodicidade das funções seno e co-seno. Uma função é dita periódica com período T > 0 se o domínio de f contém (x+T) sempre que contiver x e se f(x+T) = f (x) para todo x. Nota-se claramente que, se T (período fundamental) é um período de f, então 2 T também o é como qualquer múltiplo inteiro de T. Em particular, as funções sen [(m x)/T] e cos [(m x)/T], m = 1, 2, . . . , são periódicas com período fundamental T = (2 L / m). Ortogonalidade das funções sen e co-seno Duas funções u e v são ditas ortogonais em x se seu produto interno é nulo, isto é, se
![As funções sen m xT e cos m xT m 1 2 As funções sen [(m x)/T] e cos [(m x)/T], m = 1, 2, .](https://slidetodoc.com/presentation_image_h/1fcc8ccd10388fd6691abdce57800b98/image-3.jpg)
As funções sen [(m x)/T] e cos [(m x)/T], m = 1, 2, . . . formam um conjunto ortogonal de funções no intervalo -L x L. Senão vejamos
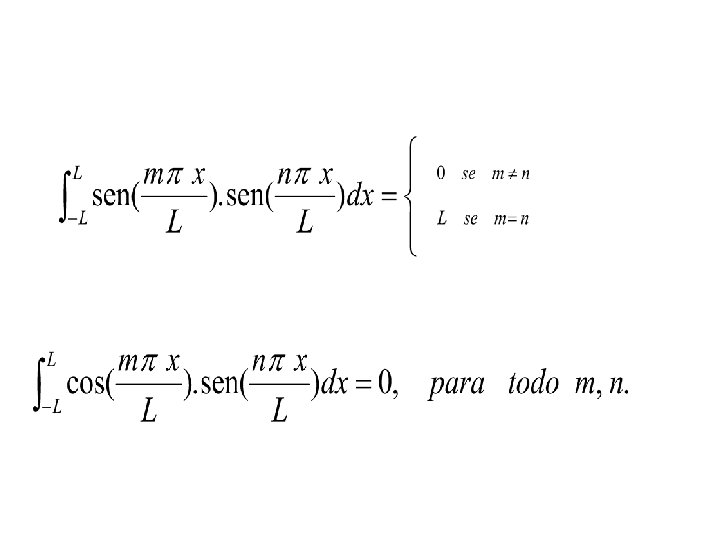

Supondo que uma série da forma converge. E considerando as propriedades de ortogonalidade vistas, temos que os coeficientes an e bn são dados por

Exemplo: Seja e suponha que f (x+6) = f (x). Encontre os coeficientes da série de Fourier de f. Como f tem período 6, segue que L = 3. Então a série de Fourier de f tem a forma onde os coeficientes an e bn são dados por
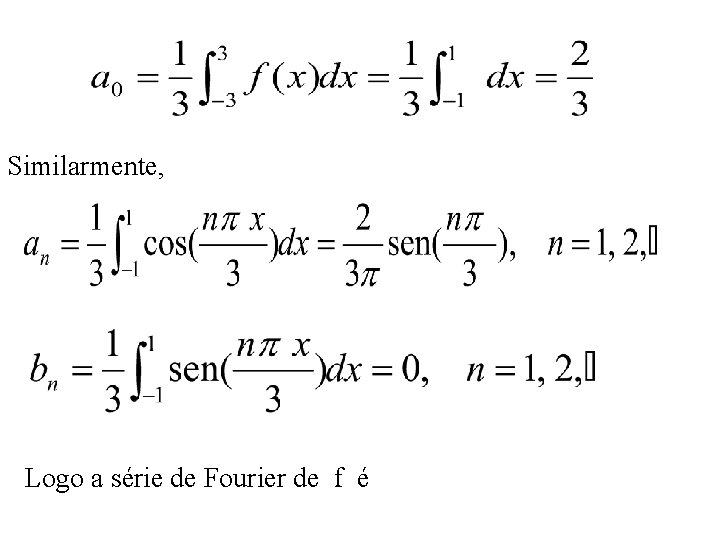
Similarmente, Logo a série de Fourier de f é

Funções pares e ímpares: Analiticamente, f é uma função par se seu domínio contém o ponto -x sempre que contiver o ponto x e se f (x) = f (-x) para cada x do domínio de f. Analogamente, f é uma função ímpar se seu domínio contém –x sempre que contiver x e se f (-x) = - f (x) para cada x no domínio de f.

Exemplos: Funções pares : 1, x 2, cos(nx), |x| e x 2 n. Funções ímpares: x, x 3, sem(nx) e x 2 n+1. A maioria das funções não é par nem ímpar. Por exemplo ex. A função identicamente nula é ímpar e par ao mesmo tempo. Propriedades elementares: a) A soma (diferença) e o produto (quociente) de duas funções pares é par. b) b) A soma (diferença) de duas funções ímpares é ímpar; o produto (quociente) de duas funções ímpares é par.

c) A soma (diferença) de uma função par e uma função ímpar não é par nem ímpar; o produto (quociente) é ímpar. d) Se f é uma função par, então e) Se f é uma função ímpar, então Como consequência das propriedades d e e, os coeficientes de Fourier de f são dados por (caso em coseno, par)

bn = 0, n = 1, 2, . . . Logo e no caso em senos, ímpar, temos: an = 0, 1, 2, . . . E a série é dada por

Equação do calor A equação do calor tem a forma 2 uxx = ut, 0 < x < L, t>0 Onde 2 é uma constante conhecida como difusividade térmica. O parâmetro 2 depende, apenas, do material do qual é feita a peça e é definida por 2 = k / s, onde k é a condutibilidade térmica, é a densidade e s é o calor específico do material utilizado. As unidades de 2 (comprimento)2 / tempo.

Alguns valores de difusividade térmica. Material 2 (cm 2 / s) Prata 1, 71 Cobre 1, 14 Alumínio 0, 86 Água 0, 00144 O problema fundamental de condução de calor é encontrar u(x, t) que satisfaz a equação diferencial 2 uxx = ut, 0 < x < t, t > 0, a condição inicial u(x, 0) = f(x), 0 x L quando t = 0 e as condições de contorno u(0, t) = 0, u(L, t) = 0, t > 0.

A equação de onda A equação da onda é dada por 2 uxx = utt, 0 < x < L, t > 0. O coeficiente constate 2 é dado por 2 = T / onde T é a tensão na corda e é a massa por unidade de comprimento do material da corda. Assim, a unidade de é comprimento / tempo. Supondo-se que as extremidades permanecem fixas, logo as condições de contorno são u(0, t) = 0, u(L, t) = 0, t 0. Como a equação é de segunda ordem em t, é razoável ter 2 condições iniciais. u(x, 0) = f(x), 0 x L e a velocidade inicial ut(x, 0) = g(x), 0 x L, onde f e g são funções dadas.

Para a consistência da equação, faz necessário supor que f(0) = f(L) = 0 e g(0) = g(L) = 0. Equação de Laplace Em duas dimensões, a equação de Laplace, que tem inúmeras aplicações, é uxx + uyy = 0, e tem três dimensões. uxx + uyy + uzz = 0. Por exemplo, em um problema de calor a duas dimensões espaciais, a temperatura u(x, y, t) tem que satisfazer a equação 2 (uxx+ yxx) = ut, onde 2 é a difusividade térmica. O problema de encontrar uma solução da equação de Laplace com valores dados na fronteira é conhecido como um problema de Dirichilet.
 Srie a
Srie a De que são formadas as rochas
De que são formadas as rochas Geografia
Geografia Composição morfológica e morfossintática
Composição morfológica e morfossintática Los seres humanos son
Los seres humanos son Oraciones bimembres
Oraciones bimembres Sufijo peto ejemplos
Sufijo peto ejemplos Protenas
Protenas Formulas bien formadas
Formulas bien formadas Miosina
Miosina Rochas formadas pelo resfriamento do magma
Rochas formadas pelo resfriamento do magma Dos cosas son infinitas
Dos cosas son infinitas O tero
O tero Hay dos cosas infinitas el universo y la estupidez humana
Hay dos cosas infinitas el universo y la estupidez humana Oração de glória ao pai
Oração de glória ao pai Ecodesarrollo dibujos
Ecodesarrollo dibujos