Sequences and Series CHAPTER 12 Section 12 1

Sequences and Series CHAPTER 12

Section 12. 1: Arithmetic Sequences and Series Objectives: • I can find the nth term and arithmetic means of an arithmetic sequence. • I can find the sum of n terms of an arithmetic series.

SEQUENCE Definition: An arithmetic sequence A common difference

Example 1: Find the next four terms in the arithmetic sequence: -5, -2, 1, … C. D. = +3 4, 7, 10, 13, … Recursive Formula Explicit Formula

Example 2: Find the 47 th term in the arithmetic sequence: -4, -1, 2, 5, … Example 3: Find the first term in the arithmetic sequence for which: and .

Example 4: Write an arithmetic sequence that has five arithmetic means between 4. 9 and 2. 5. 4. 5 4. 1 3. 7 3. 3 2. 9 4. 9, _____, _____, 2. 5

DIFFERENCE BETWEEN SEQUNECE AND SERIES Arithmetic Sequence Arithmetic Series -9, -3, 3, 9 -9 + -3 + 9 The symbol, , called: the nth partial sum.

Example 5: Find the sum of the first 60 terms in the arithmetic series 9 + 14 + 19 + … + 304.

Warm-Up Use the sequence to answer the questions 7. 2, 6. 6, 6, 5. 4, … A. Write the Recursive and Explicit formulas B. Find the 30 th Term C. Find the 18 th Partial Sum

Fill in Reference page for 12. 1 • Recursive Arithmetic Sequence • Explicit Arithmetic Sequence • Arithmetic Series

Section 12. 2: Geometric Sequences and Series Objectives: • Find the nth term and geometric means of a geometric sequence. • Find the sum of n terms of a geometric sequence.

Definition: A geometric sequence Example 1: Determine the common ratio and find the next three terms in each sequence: r = -. 5 a. b. r – 1, -3 r + 3, 9 r – 9, … Common ratio, “r” r = -3

Definition: The nth term of a geometric sequence Recursive Explicit

Example 2: Find an approximation for the 23 rd term in the sequence: 256, -179. 2, 125. 44, …

Example 3: G 1 = 26000 G 2 = year 1 G 3 = year 2 G 4 = year 3 G 5 = year 4 A new car costing $26, 000 depreciates at a rate of 40% per year four years. Find the value of the car at the end of four years. • NOTE: Geometric sequences can represent growth or decay.

Example 4: Write a sequence that has two geometric means between 48 and -750. -120 300 48, _________, -750

Definition: A geometric series Example 5: Find the sum of the first ten terms of the geometric series 16 – 48 + 144 – 432 + …

Do homework TOGETHER!!!!

Warm-Up 28/3 56/9 14, ____, 112/27…. • Find the two geometric means between the given numbers. g 4 = 14 r 3 r = 2/3 112/27 = 14 r 3 • Write a recursive and Explicit formula for both. g 1 = 14 gn = 2/3 gn-1 gn = 14(2/3)n-1

Warm-Up • Quick Check Self-Quiz (ungraded) • On the front desk • ONLY 5 minutes after the bell!!!!

Fill in reference sheet for Geometric!

Section 12. 3: Infinite Sequences and Series Objectives: • Find the limit of the terms of an infinite sequence. • Find the sum of an infinite geometric series.

Limit Notation: Example 1: • Estimate the limit of Bill Gates RULE!!!!!

v Example 2: Find each limit a. b. 3 Example 1: Estimate the limi 5

Example 2 continued… Find each limit. c. d.

e.

Definitions (Sum of an Infinite Series): ***Lets think about growing sequences for a minute*** Arithmetic ……… keeps growing forever…. . Geometric Ratio: r > 1 ……. keeps growing forever…. . Ratio: r = 1 ……numbers stay the same, but it still keeps growing forever. . . Ratio: r < 1 ………numbers get smaller and smaller…. . . hmmm interesting…….

(Sum of an Infinite *Geometric* Series):

Example 4: Find the sum of the series 21 – 3 +

Example 5: Write as a fraction.

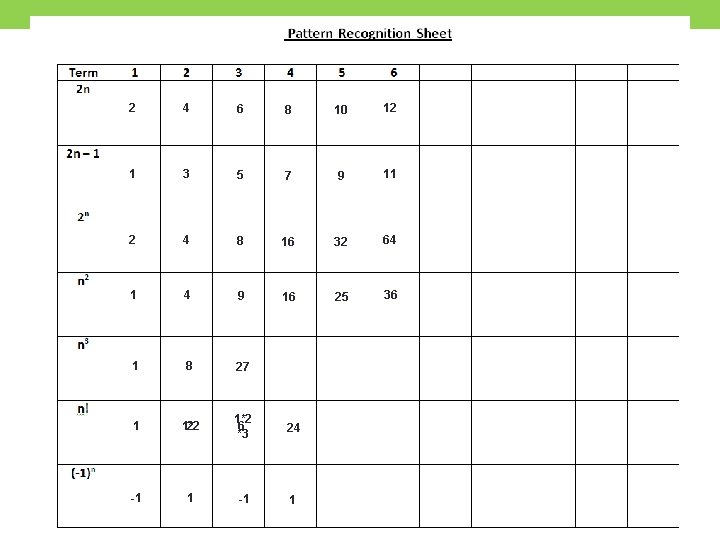
Find the pattern…. write the equation 1. 5, 7, 9, 11, …… 2. 6, 12, 24, 48…. . 3. 7, 7/3, 7/9, 7/27, … 4. 1, 4, 9, 16, …. . Always look for Arithmetic/Geometric FIRST Then, refer to “other” patterns

2 4 1 Pattern Recognition 6 8 10 12 3 5 7 9 11 2 4 8 16 32 64 1 4 9 16 25 36 1 8 27 1 1*2 2 1*2 6 *3 24 -1 1

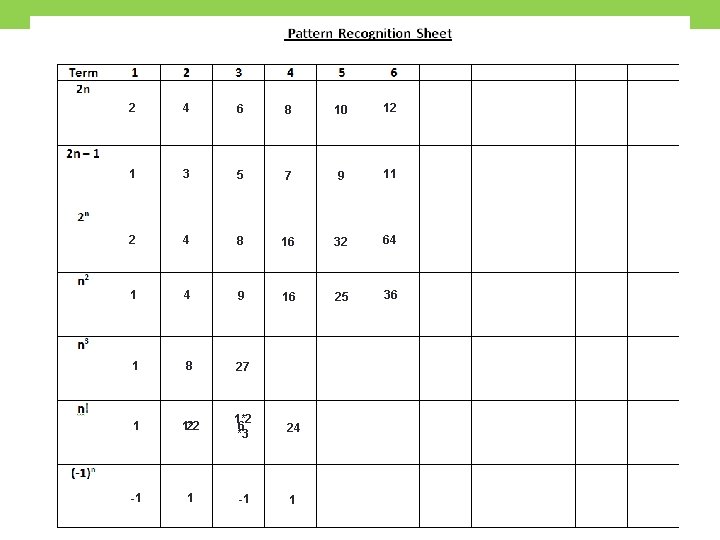
10 minutes for pattern recognition hw

Warm-Up • Find your table’s Partial Sum (Sn), for the sequence defined by gn = 3(. 2)n-1 • S 1= • S 2= • S 3= • S 4= • S 5= • S 6= • S 7= • S 8=

2 4 1 Pattern Recognition 6 8 10 12 3 5 7 9 11 2 4 8 16 32 64 1 4 9 16 25 36 1 8 27 1 1*2 2 1*2 6 *3 24 -1 1

Section 12. 4: Convergent and Divergent Series Objectives: • Determine whether a series is convergent or divergent.

Definitions: • Converge Approaches something • Diverge Keeps growing/decaying to infinity

Example 1: Determine whether each arithmetic or geometric series is convergent or divergent. a. convergent R = -. 5 divergent R = 2 geometric b. 2 + 4 + 8 + 16 + … geometric c. 10 + 8. 5 + 7 + 5. 5 + … Arithmetic…. divergent

Ratio Test: r>1 divergent r<1 convergent r= 1 “No results” NOTE about the ratio test, this test can only be used when all terms of the series are positive.

Example 2 b. (do this one first)

Definition: (found in section 12. 5) The expression n! (n factorial) is defined as follows for n, an integer greater than zero. n! = n(n – 1)(n – 2)…. 1 • Question: What is

Example 2: Use the ratio test to determine whether each series is convergent or divergent. a. lim lim r<1, therefore convergent

Example 2 continued… Use the ratio test to determine whether each series is convergent or divergent. c. d. Harmonic…

Warm-Up Determine whether the following series converge/diverge: 1) 4/3, 4/9, 4/27……. 2) 3. 2 + 3. 84 + 4. 608 + 5. 5296…

Patterns worksheet • 1. 5 n 1. n! = • “n – factorial” n(n-1)(n-2)(n-3)…. . (1) ex: 4! = 4*3*2*1 = 24 2. Other cool patterns…. . a. 1, 4, 9, 16, 25, ……. . n 2 b. 1, 2, 6, 24, 120, …. n! c. 1, 8, 27, 64, …. . n 3 • 2. (3/2)2 n • 3. -3 n + 10 • 4. 2 n! • 5. an = an-1 + an-2 • 6. n 3 • 7. n 2 + 1 • 8. (n-1)! • 9 n/2 n • 10. n/(n+1)

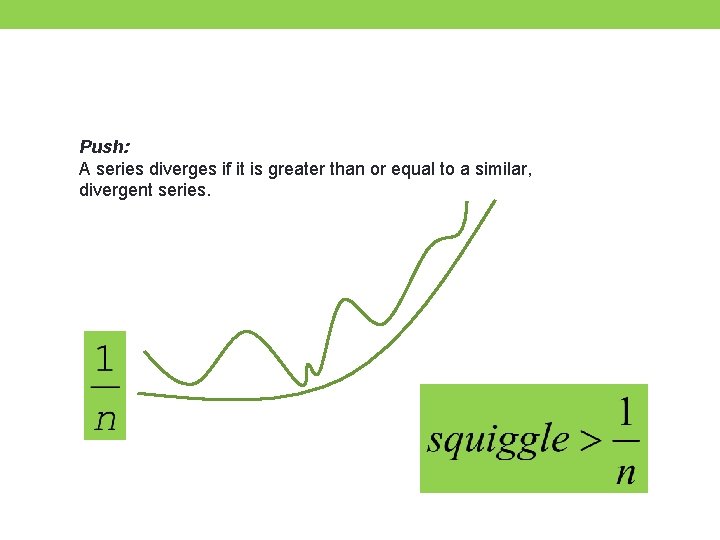
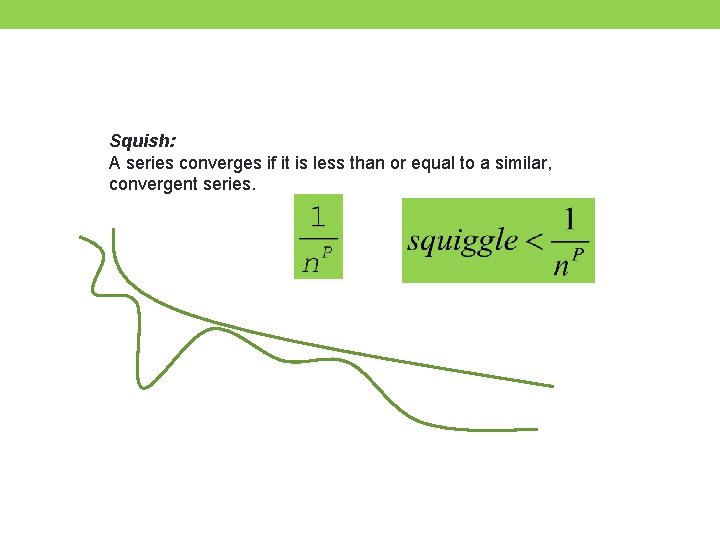
Comparison Test: Wh en n >1 Squish: A series converges if it is less than or equal to a similar, convergent series. Push: A series diverges if it is greater than or equal to a similar, divergent series.

Push: A series diverges if it is greater than or equal to a similar, divergent series.

Squish: A series converges if it is less than or equal to a similar, convergent series.

Example 3: Use the comparison test to determine whether the following series are convergent or divergent: a. Divergent

Example 3: Use the comparison test to determine whether the following series are convergent or divergent: b. Convergent

Warm-Up 1. What is the pattern? 0, 3, 8, 15, … 2. What is the pattern? 4, 8, 12, 16, ……

To this point: Arithmetic recursive, explicit Geometric recursive, explicit Sn for BOTH S for geometric <1 Patterns! Convergence Divergence Ratio Test Comparison Test

Section 12. 5: Sigma Notation and the nth Term Objectives: • Use sigma notation.

Definition: Sigma notation m ter Nth Starting term!

Example 1: Write each expression in expanded form and then find the sum: rm th te N a. Starting term!

b. Infinite series…does that even make sense?

Example 2: During a nine-hole charity golf match, one player presents the following proposition: The loser of the first hole will pay $1 to charity, and each succeeding hole will be worth twice as much as the hole immediately preceding it. A. How much would a losing player pay on the 4 th hole? 1, 2, 4, 8 $8 B. How much would a player pay if he or she lost all nine holes? 1+2+4+8+16+32+64+128+256 = 511 C. Represent this sum using sigma notation.

Example 3: Not geometric or arithmetic? ? Express the series 15 + 24 + 35 + 48 + … + 143 using sigma notation. term h t N Perf ect s quar es, m Starting term! inus one .

Example 4 (CHALLENGE PROBLEM): You’ll need your partners for this one! A lte rna tin Arithmetic… Express the series using sigma notation. g, st art ing at se c connected to factorials… 1, 2, 6, 24, 129…. on d te r m

Section 12. 6: The Binomial Theorem Objectives: • Use the Binomial Theorem to expand binomials.

Announcements • Typos in homework……. • #6 “i” should be a “t” • #7 3, 6, 9, 12, 15

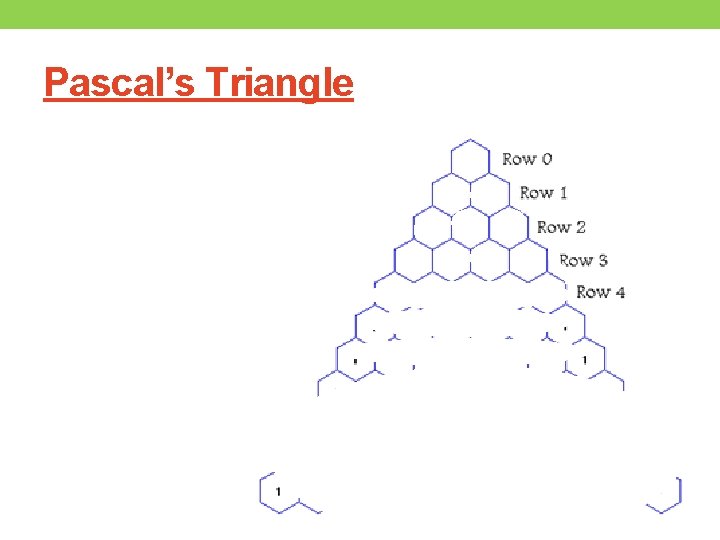
Pascal’s Triangle

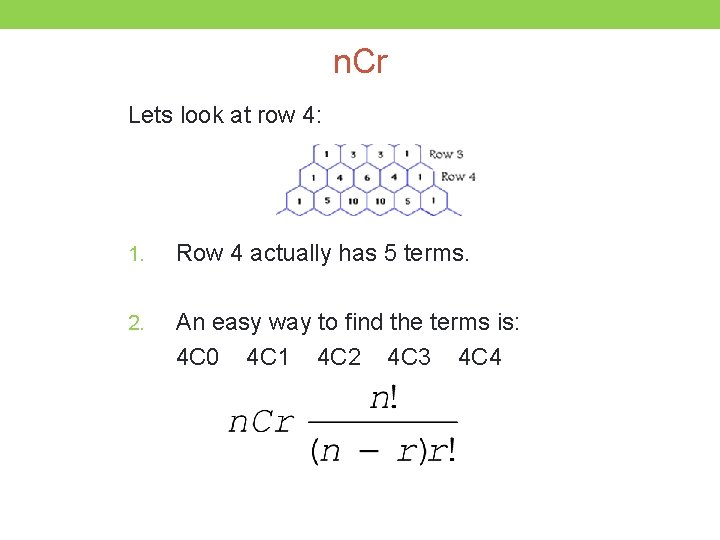
n. Cr Lets look at row 4: 1. Row 4 actually has 5 terms. 2. An easy way to find the terms is: 4 C 0 4 C 1 4 C 2 4 C 3 4 C 4

Example 1: • Use Pascal’s Triangle to expand each binomial. a. (x + y)6 Sixth Row (6 Cr): 1 6 15 20 15 6 1 5 x 1 y 4 x 2 y 3 x 3 y 2 x 4 y 1 x 1 y 0 6 1 +6 +15 +20 +15 +6 +1 x 6 x y 0 y

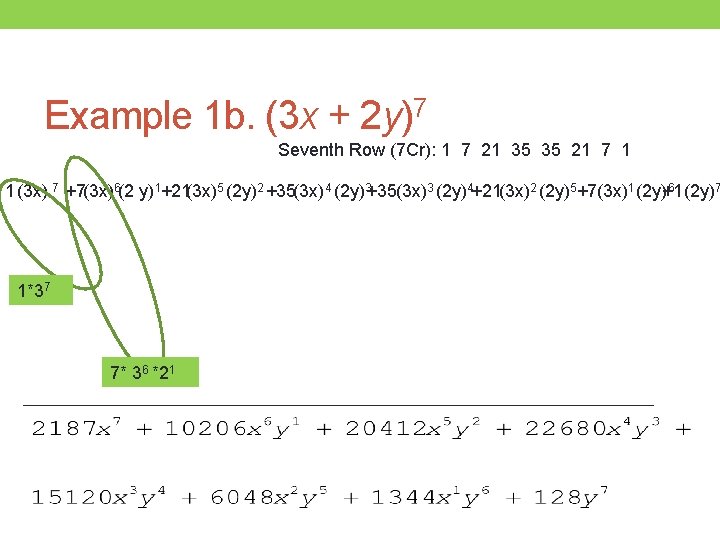
Example 1 b. (3 x + 2 y)7 Seventh Row (7 Cr): 1 7 21 35 35 21 7 1 1 (2 y) 5 (3 x) 2 (2 y) 4 (3 x) 3 (2 y) 3 (3 x) 4 (2 y) 2 (3 x) 5 (2 y) 1 6 (2 y)7 1 +7 +21 +35 +21 +7 +1 (3 x) 7 (2 y) (3 x)6 (3 x) 1*37 7* 36 *21

Example 2: A quality control manager determines that out of a batch of 10 components, at most 4 are defective. How many of the possible groups of defective and non-defective components have at most 4 defective components? At most 4 defective: 4 d 3 d 2 d 1 d 0 d 210 120 45 10 1 = 386

Example 3 (Do as warm-up): Use the Binomial Theorem (pascals) to expand: (2 x – y)6.

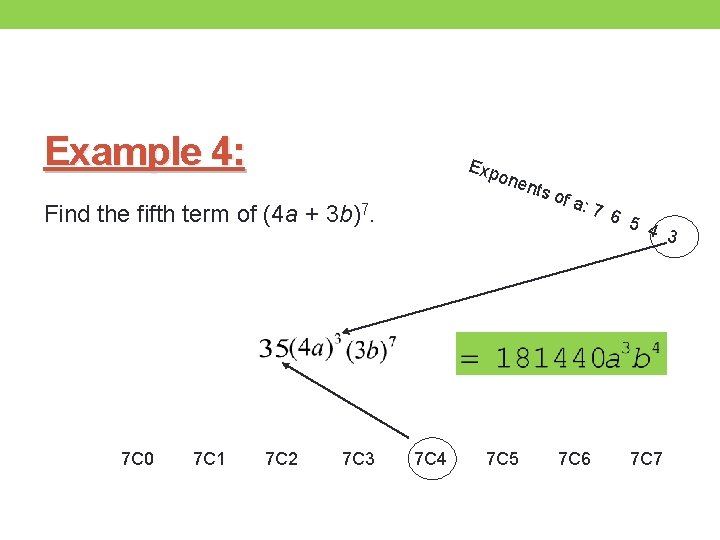
Example 4: Exp one nts of a : Find the fifth term of (4 a + 3 b)7. 7 C 0 7 C 1 7 C 2 7 C 3 7 C 4 7 C 5 7 6 7 C 6 5 4 3 7 C 7

Review…. .

Arithmetic Sequences Recursive Explicit Series

Geometric Sequences Recursive Explicit Series Partial Infinite

Convergence vs. Divergence r>1 divergent r<1 convergent r= 1 “No results” Ratio Test Comparison Test Squish: A series converges if it is less than or equal to a similar, convergent series. Push: A series diverges if it is greater than or equal to a similar, divergent series.

• Sigma Notation • The Binomial Thm

Definition (Binomial Thm): This is just another way of finding the binomial expansion. We can keep using pascals triangle and combinations too…