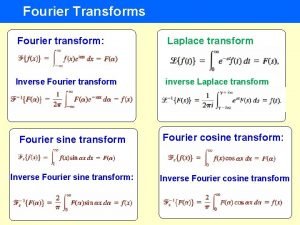
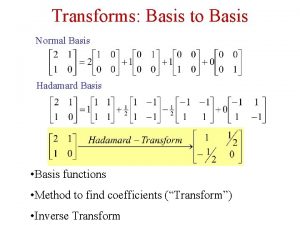
Orthogonal Transforms Fourier Cosine KL Walsh Hadamard Orthogonal




















































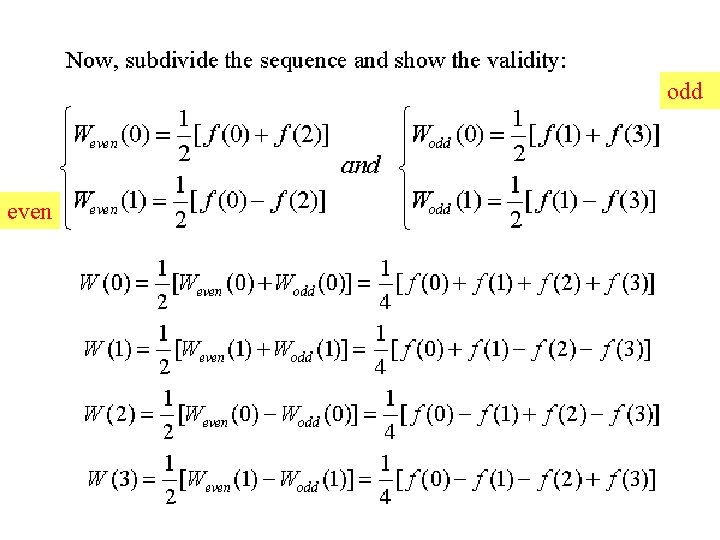

























- Slides: 87

Orthogonal Transforms Fourier Cosine KL Walsh Hadamard

Orthogonal Functions






Mean Square Error



Important result

• We want to minimize this kinds of errors. • Other error measures are also used.

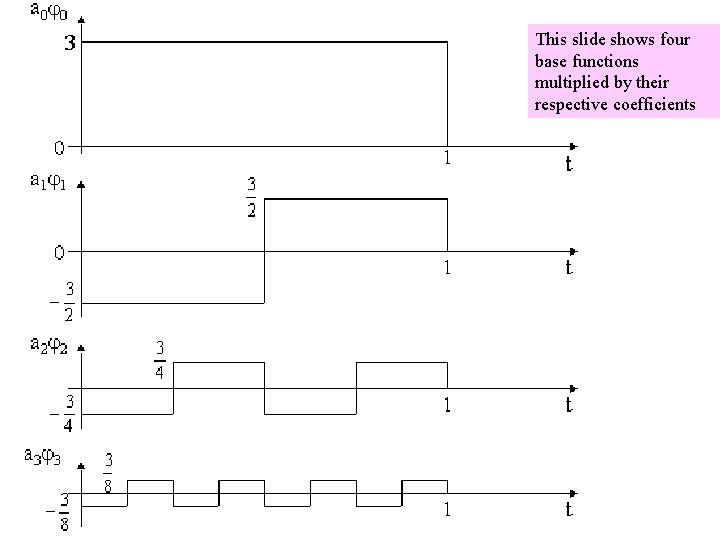
Example of arbitrary basis functions being rectangular waves

This determining first function determines next functions

0 1


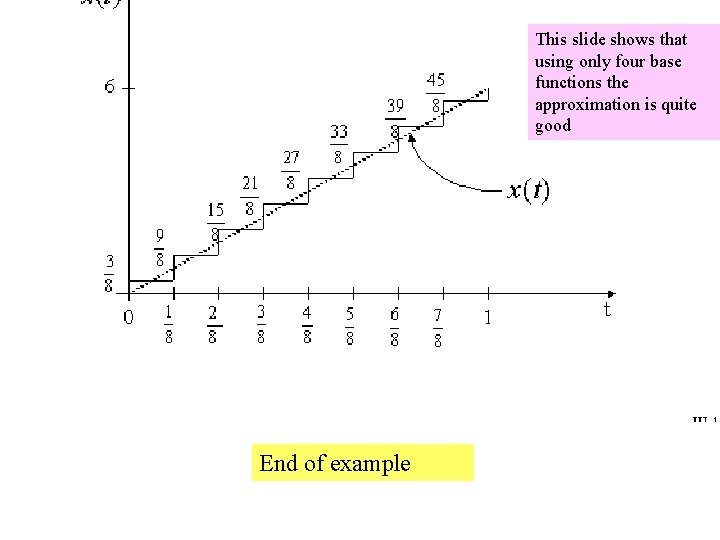
Small error with just 3 coefficients

This slide shows four base functions multiplied by their respective coefficients

This slide shows that using only four base functions the approximation is quite good End of example

General Orthogonal Transforms

Extending general transforms to 2 dimensions

Orthogonal and separable Image Transforms Forward transform inverse transform separable

Unitary Transforms • Unitary Transformation for 1 -Dim. Sequence – Series representation of – Basis vectors : – Energy conservation : Here is the proof

• Unitary Transformation for 2 -Dim. Sequence – Definition : – Basis images : – Orthonormality and completeness properties • Orthonormality : • Completeness :

• Unitary Transformation for 2 -Dim. Sequence – Separable Unitary Transforms • separable transform reduces the number of multiplications and additions from to – Energy conservation

Fourier Transform separable

Extension of 1 -D Fourier Transform to two dimensions



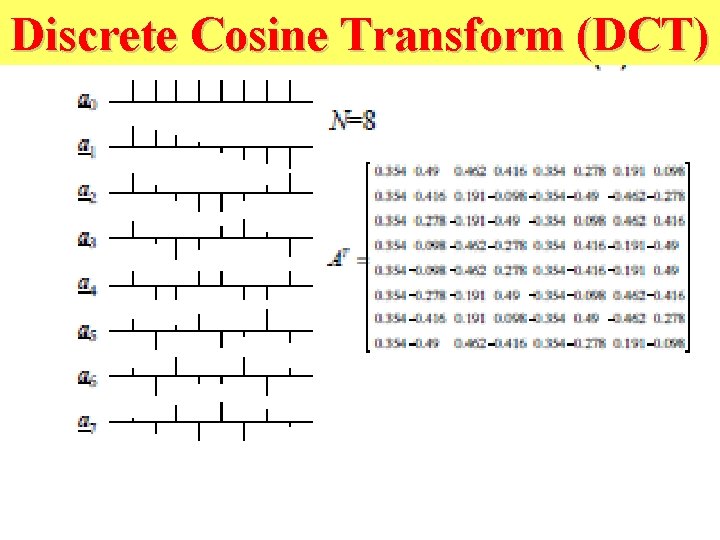
Discrete Cosine Transform (DCT)

Discrete Cosine Transform (DCT)

Discrete Cosine Transform (Compare to WH transform)

DCT is an orthogonal transformm so its inverse kernel is the same as forward kernel

2 -D Discrete Cosine Transform

2 -D Discrete Cosine Transform

Properties of DCT: real, orthogonal, energycompacting, eigenvector-based

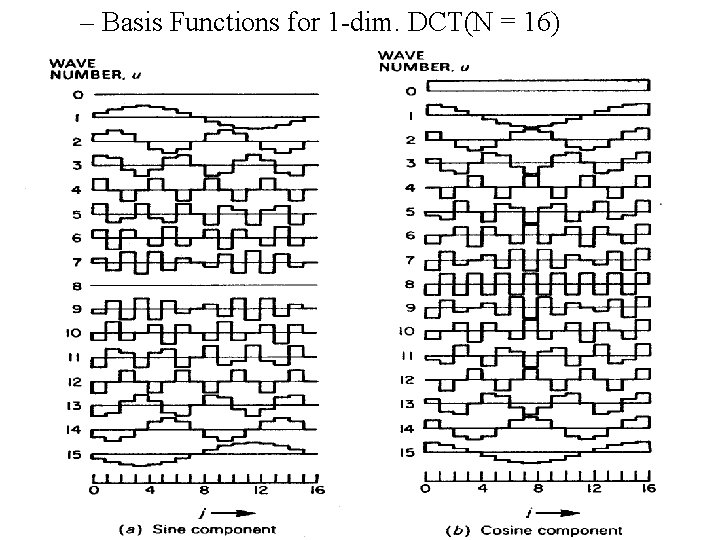
– Basis Functions for 1 -dim. DCT(N = 16)

There are many DCT fast algorithms and hardware designs. Many fast algorithms are available fast algorithm : Lee(1 -D), Lee-Cho(2 -D) VLSI algorithm : regularity, local interconnection, moduality ref: 1. Nam Ik Cho and Sang Uk Lee, “Fast algorithm and implementation of 2 -D DCT. ” IEEE Trans Circuits and Systems, vol. 38, no. 3, pp. 297 -305, March 1991. 2. Nam Ik Cho and Sang Uk Lee, “DCT algorithm for VLSI parallel implementation” IEEE Trans. ASSP, vol. ASSP-38, no. 1, pp. 121 -127, Jan, 1990.

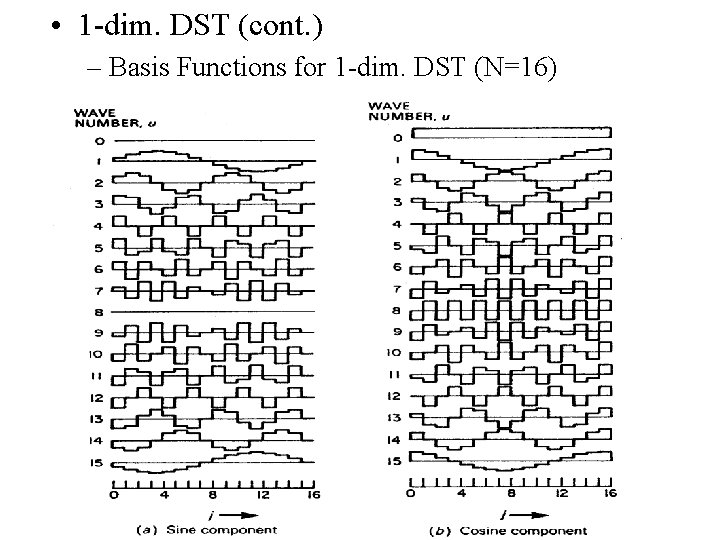
Discrete Sine Transform(DST) Similar to DCT.

• 1 -dim. DST (cont. ) – Basis Functions for 1 -dim. DST (N=16)

Karhunen-Leove (KL) Transform (Principal Component Analisis, PCA) Covariance matrix


• Methodology − Suppose x 1, x 2, . . . , x. M are N x 1 vectors

• Methodology – cont.

• Linear transformation implied by KL transform − The linear transformation RN RK that performs the dimensionality reduction is: 46

Principal Component Analysis (PCA) • Geometric interpretation − PCA projects the data along the directions where the data varies the most. − These directions are determined by the eigenvectors of the covariance matrix corresponding to the largest eigenvalues. − The magnitude of the eigenvalues corresponds to the variance of the data along the eigenvector directions. 47

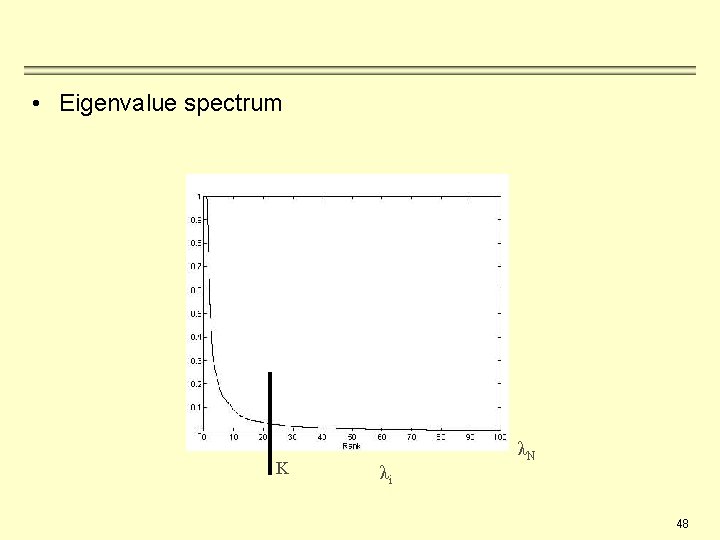
• Eigenvalue spectrum K λi λN 48

Principal Component Analysis (PCA) • How many principal components to keep? − To choose K, you can use the following criterion (total variations preserved) : 49

• Representing faces onto this basis 50

Walsh Transform

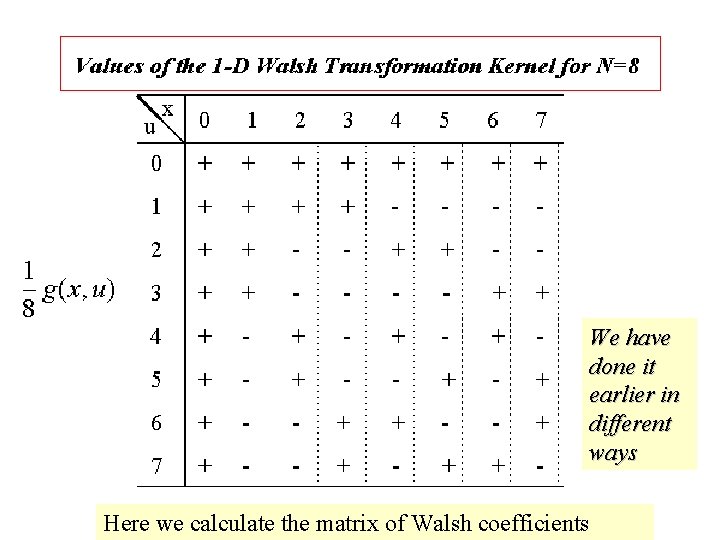
Here we calculate the matrix of Walsh coefficients

Here we calculate the matrix of Walsh coefficients

Here we calculate the matrix of Walsh coefficients

We have done it earlier in different ways Here we calculate the matrix of Walsh coefficients

Symmetry of Walsh Think about other transforms that you know, are they symmetric?

Two-Dimensional Walsh Transform

Two-dimensional Walsh Inverse Two-dimensional Walsh

Properties of Walsh Transforms

Here is the separable 2 -Dim Inverse Walsh

Example for N=4
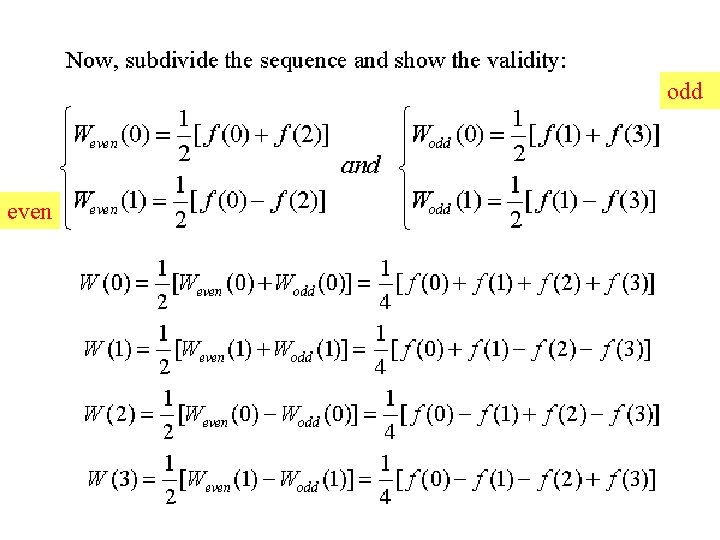
odd even

Discuss the importance of this figure

Hadamard Transform We will go quickly through this material since it is very similar to Walsh


separable

Example of calculating Hadamard coefficients – analogous to what was before








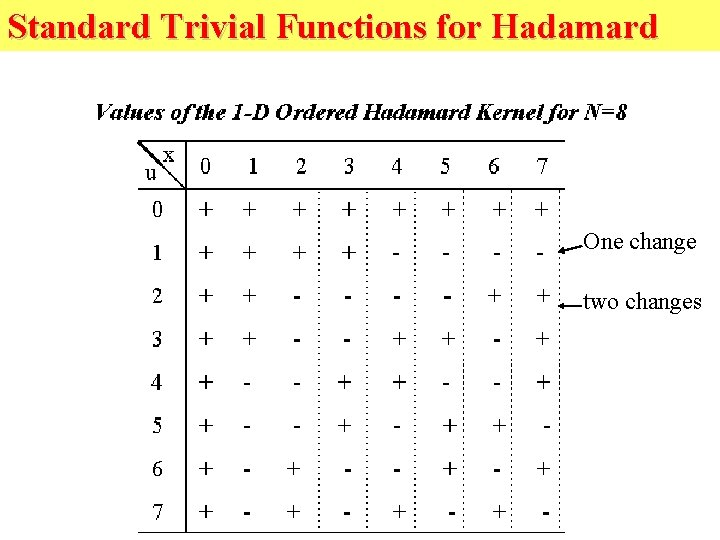
Standard Trivial Functions for Hadamard One change two changes


Discrete Walsh-Hadamard transform (Summary) Now we meet our old friend in a new light again!





Haar Transform • Haar transform – Haar function (1910, Haar) : periodic, orthonormal, complete Nonsinusoidal orthogonal function



Slant transform



 Uu
Uu Parent functions and transformations
Parent functions and transformations Hadamard transform
Hadamard transform Hadamard transform in digital image processing
Hadamard transform in digital image processing Hadamard's theorem in complex analysis
Hadamard's theorem in complex analysis Qubit gates
Qubit gates Fourier transform odd function
Fourier transform odd function Fourier cosine transform of f(x)=1
Fourier cosine transform of f(x)=1 Half range series
Half range series Generalized fourier series
Generalized fourier series Fourier series and orthogonal functions
Fourier series and orthogonal functions Orthogonal functions in fourier series
Orthogonal functions in fourier series Dr claire walsh
Dr claire walsh D walsh sdsu
D walsh sdsu Lxc container consulting
Lxc container consulting Iquips
Iquips Indeks 2
Indeks 2 James walsh brown
James walsh brown Walsh v wilkie
Walsh v wilkie Image transforms in digital image processing
Image transforms in digital image processing Social problem is seen as a deviation
Social problem is seen as a deviation A. jelaskan tentang konsep angka indeks
A. jelaskan tentang konsep angka indeks Conor walsh harvard
Conor walsh harvard Robyn walsh slp
Robyn walsh slp Bernadine walsh
Bernadine walsh Haar transform in digital image processing for n=8
Haar transform in digital image processing for n=8 Ratonzote
Ratonzote Olga walsh
Olga walsh B. timothy walsh
B. timothy walsh Dr lorraine walsh
Dr lorraine walsh Mary g walsh writing center
Mary g walsh writing center Landis walsh
Landis walsh Bud walsh into the wild
Bud walsh into the wild Elizabeth walsh
Elizabeth walsh William j walsh phd
William j walsh phd Psy walsh
Psy walsh Pearl sydenstricker buck
Pearl sydenstricker buck Development of drama
Development of drama Pole vault energy transformation
Pole vault energy transformation Integrator z transform
Integrator z transform The unit that transform data into information
The unit that transform data into information Which phase transforms srs document into a form easily
Which phase transforms srs document into a form easily Inverse z transform table
Inverse z transform table Image transforms
Image transforms Transforms of discontinuous functions
Transforms of discontinuous functions Transforms of derivatives
Transforms of derivatives Transforms eroded parts of earth's surface into lakes
Transforms eroded parts of earth's surface into lakes How is odysseus able to withstand circe's magic
How is odysseus able to withstand circe's magic Photosynthesis transforms light energy into chemical energy
Photosynthesis transforms light energy into chemical energy Walang sugat setting
Walang sugat setting Friction transforms mechanical energy to
Friction transforms mechanical energy to Laplace transformation formula
Laplace transformation formula 9-5 practice graphing trigonometric functions
9-5 practice graphing trigonometric functions The sine and cosine curves intersect infinitely
The sine and cosine curves intersect infinitely Cos a
Cos a Graph of sine and cosine functions
Graph of sine and cosine functions Graph transformations
Graph transformations Sine cosine tangent quadrants
Sine cosine tangent quadrants Cosine ratio examples
Cosine ratio examples Cosine similarity
Cosine similarity Symmetry of tan graph
Symmetry of tan graph Tan = opp/adj
Tan = opp/adj Trig ratios
Trig ratios Sinusoids lesson 4-4
Sinusoids lesson 4-4 Cos fraction
Cos fraction Period of sin
Period of sin How to find an obtuse angle using the sine rule
How to find an obtuse angle using the sine rule Dirichlet discontinuous factor
Dirichlet discontinuous factor Inverse cosine
Inverse cosine 28+15
28+15 What is a quotient identity
What is a quotient identity Range of inverse sine function
Range of inverse sine function Domain of a constant function
Domain of a constant function Tan geometry formula
Tan geometry formula Trigonometry gcse foundation
Trigonometry gcse foundation Graph of sine and cosine functions
Graph of sine and cosine functions 6-5 practice translations of sine and cosine functions
6-5 practice translations of sine and cosine functions Cosine and sine graph
Cosine and sine graph Derivative of inverse cosine
Derivative of inverse cosine Midline of cosine function
Midline of cosine function Cosine rule
Cosine rule Triangle length rule
Triangle length rule Sine maze
Sine maze Trigonometry dr frost
Trigonometry dr frost Practice 9-1 the tangent ratio
Practice 9-1 the tangent ratio The sine graph
The sine graph Cosine integral
Cosine integral Sin 120°
Sin 120°