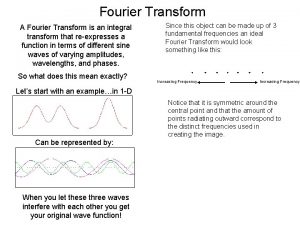
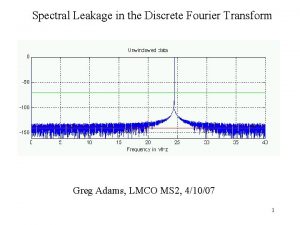
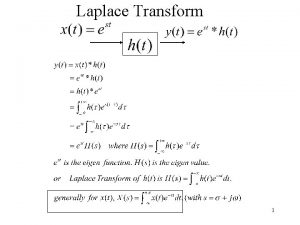Fourier Series Fourier Integral Fourier Transform Group 9







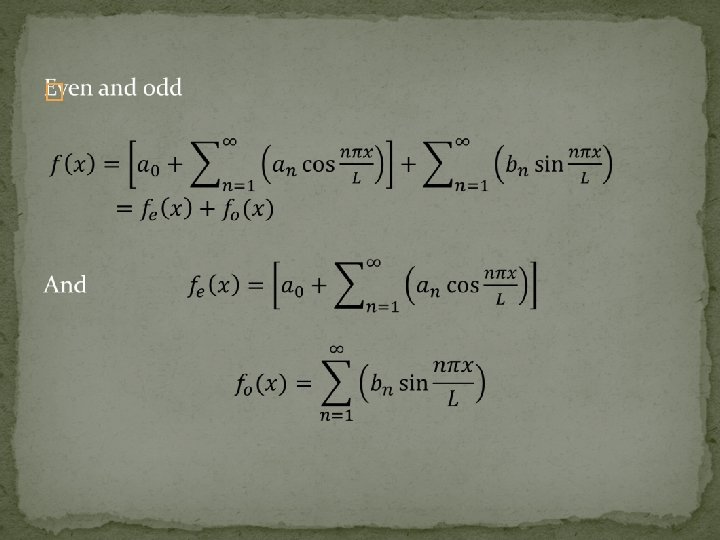

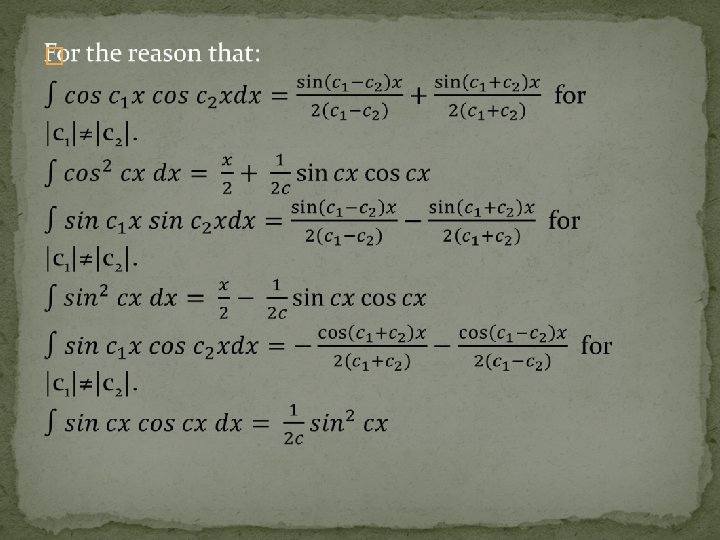









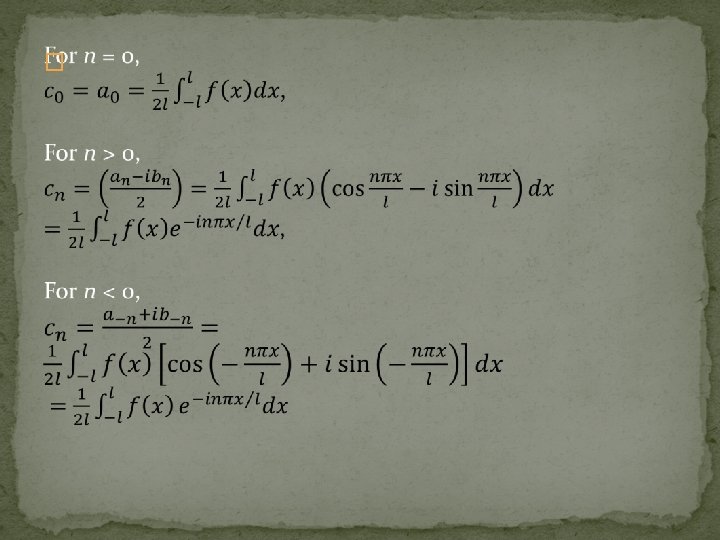

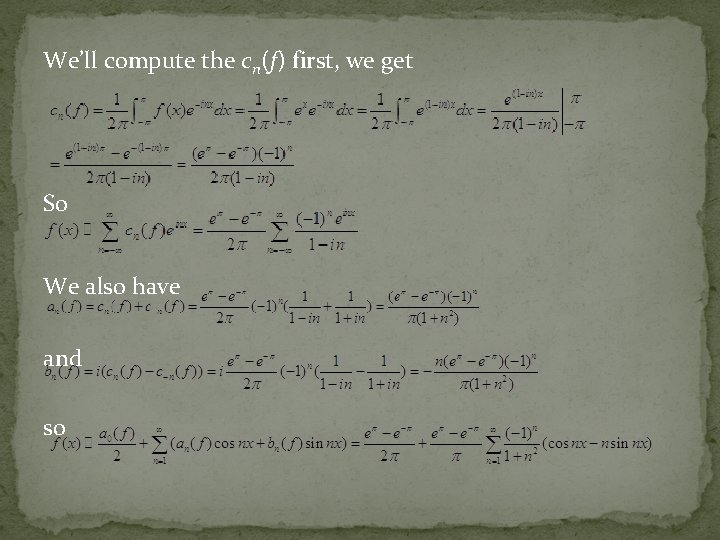


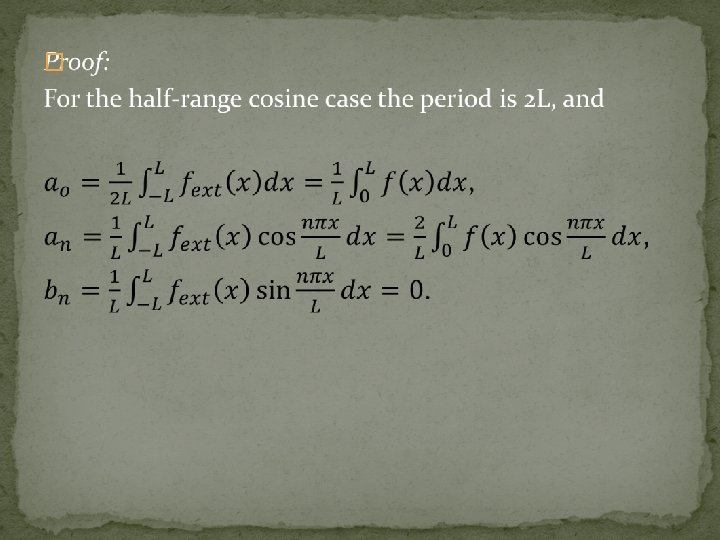



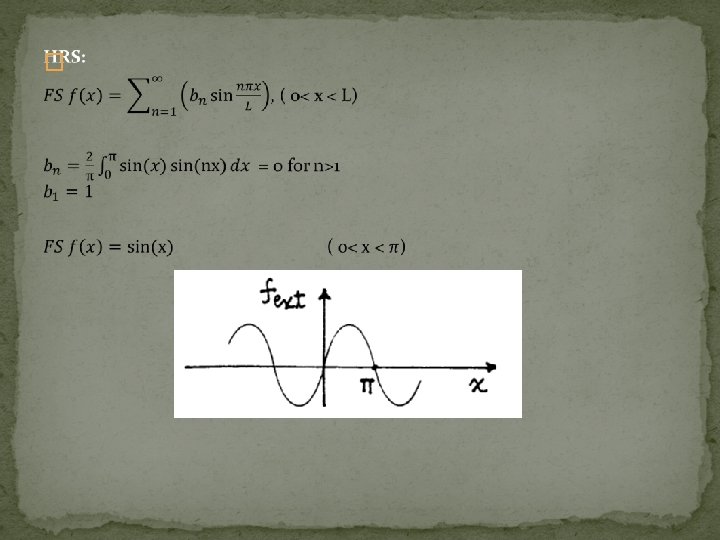
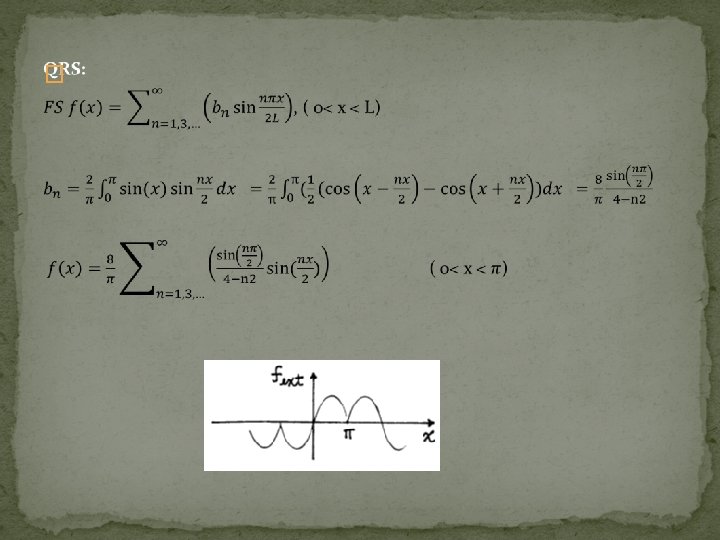




![17. 6 Vector Space Approach Some definitions: � Function space. Cp[a, b] of all 17. 6 Vector Space Approach Some definitions: � Function space. Cp[a, b] of all](https://slidetodoc.com/presentation_image_h/016b7150f349834e79886bfef3b9033d/image-41.jpg)










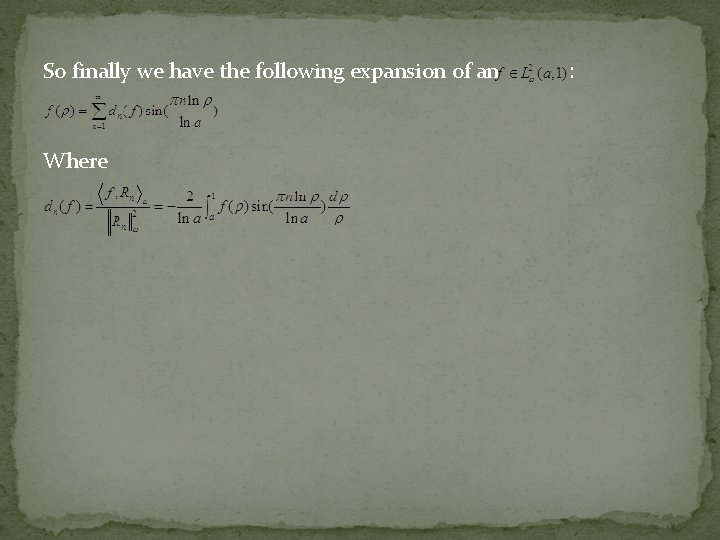

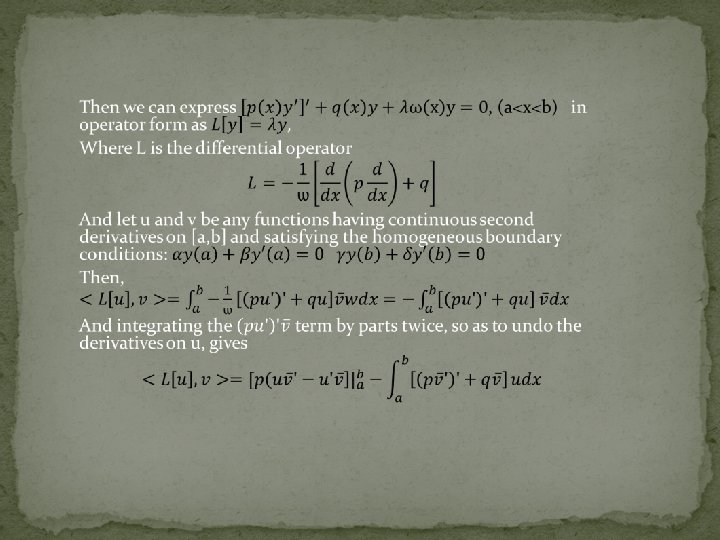













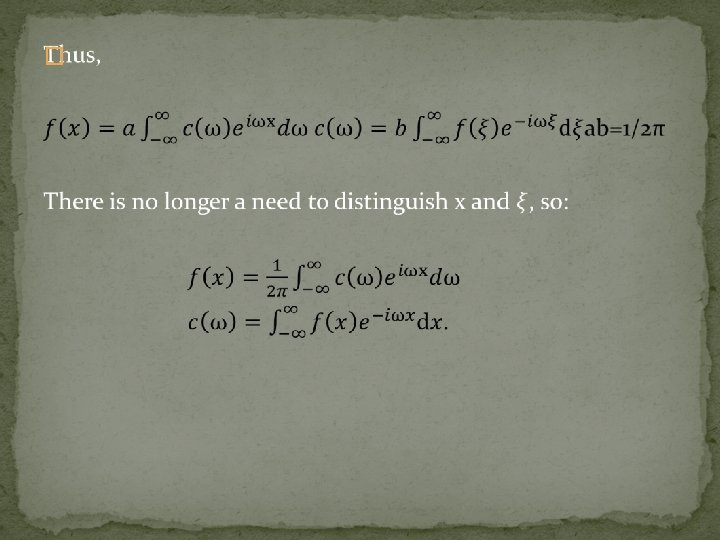

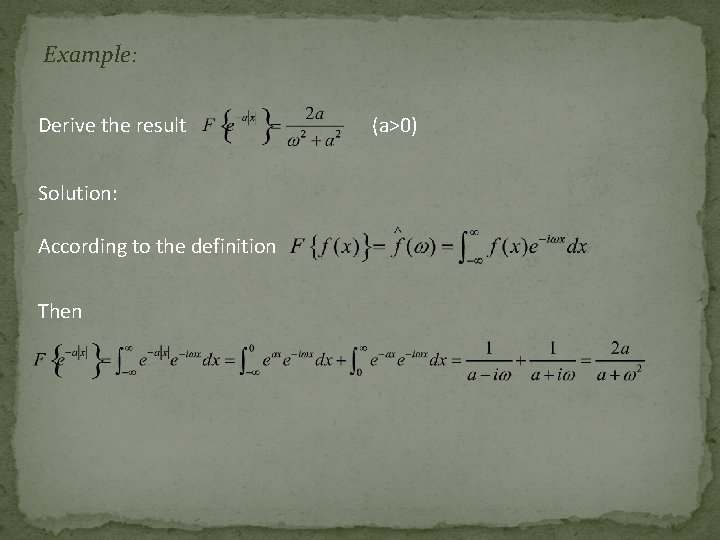










- Slides: 81

Fourier Series , Fourier Integral, Fourier Transform Group #9 Yizhi Hong Jiaqi Zhang Nicholas Zentay Sagar Lonkar

17. 1 Introduction Main Work: Théorie analytique de la chaleur (The Analytic Theory of Heat) • Any function of a variable, whether continuous or discontinuous, can be expanded in a series of sines of multiples of the variable (Incorrect) • The concept of dimensional homogeneity in equations • Proposal of his partial differential equation for conductive diffusion of heat Jean Baptiste Joseph Fourier (Mar 21 st 1768 –May 16 th 1830) Discovery of the "greenhouse effect" French mathematician, physicist http: //en. wikipedia. org/wiki/Joseph_Fourier

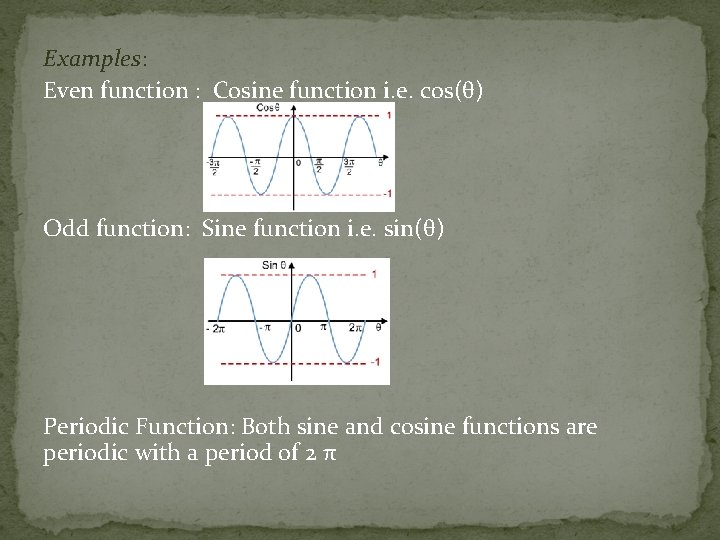
17. 2 Even, Odd, and Periodic Functions �


Examples: Even function : Cosine function i. e. cos(θ) Odd function: Sine function i. e. sin(θ) Periodic Function: Both sine and cosine functions are periodic with a period of 2 π

17. 3 Fourier Series of a Periodic Function �

For FS f to represent f we need the series to converge, and we need its sum function to be the same as the original function f(x).

THEOREM 17. 3. 1 Fourier Convergence Theroem �
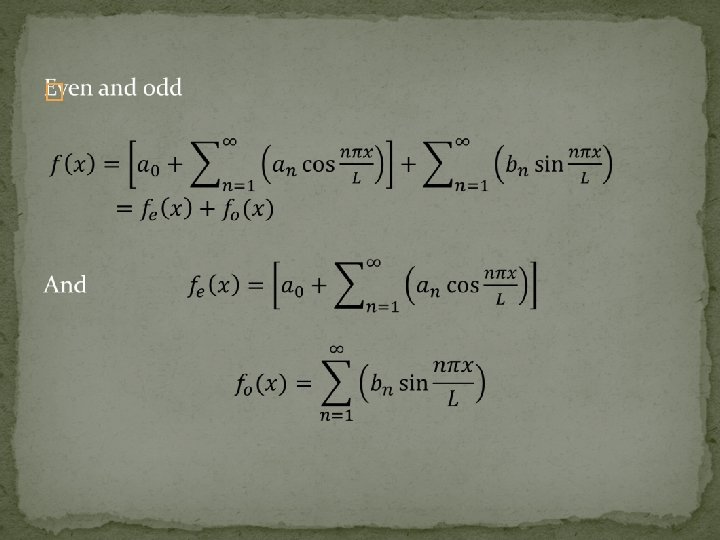

Proof of Euler Formulas
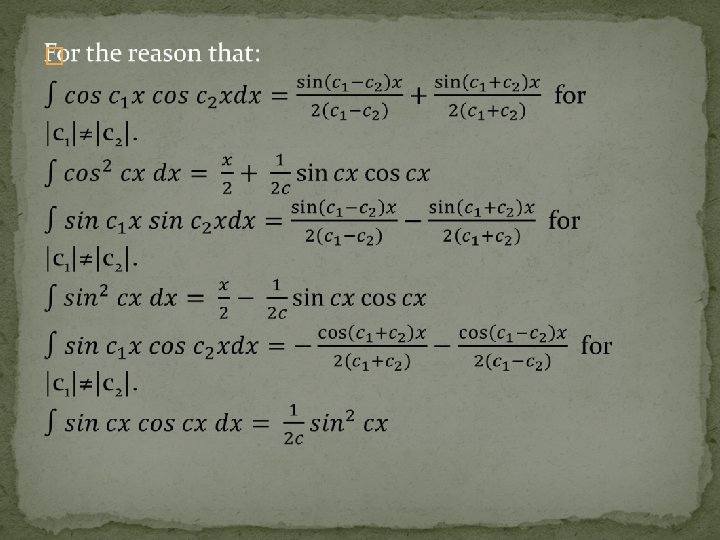


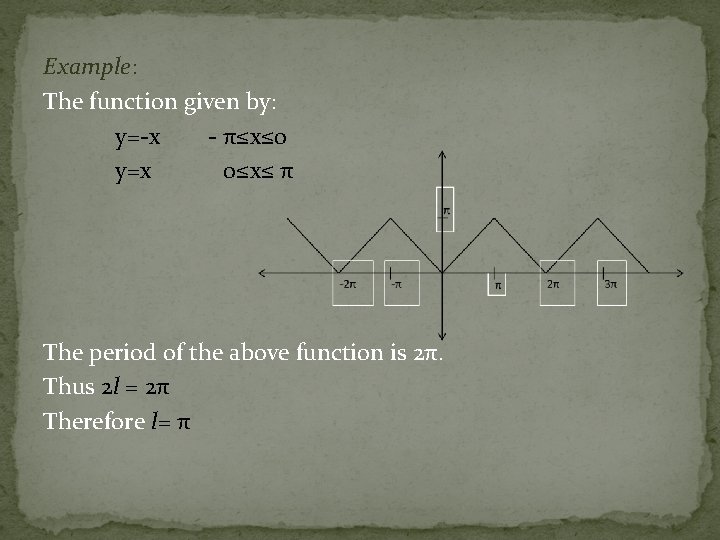
Example: The function given by: y=-x - π≤x≤ 0 y=x 0≤x≤ π The period of the above function is 2π. Thus 2 l = 2π Therefore l= π


s 0 s 1 s 3 s 5

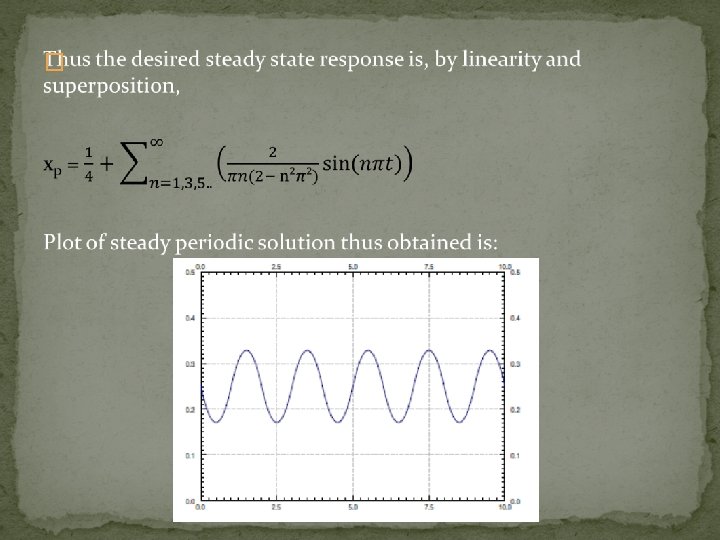
Example: Periodically forced oscillation: mass-spring system k m F(t) m = mass c = damping factor k = spring constant F(t) = 2 L- periodic forcing function mx’’(t) + cx’(t) + k x(t) = F(t) http: //www. jirka. org/diffyqs/ Differential Equations for Engineers

The particular solution xp of the above equation is periodic with the same period as F(t). The coefficients are k=2, and m=1 and c=0 (for simplicity). The units are the mks units (meters-kilograms- seconds). There is a jetpack strapped to the mass, which fires with a force of 1 newton for 1 second and then is off for 1 second, and so on. We want to find the steady periodic solution. The equation is: x’’ + 2 x = F(t) Where F(t) => 0 if -1<t<0 1 if 0<t<1




Complex exponential form for Fourier series �


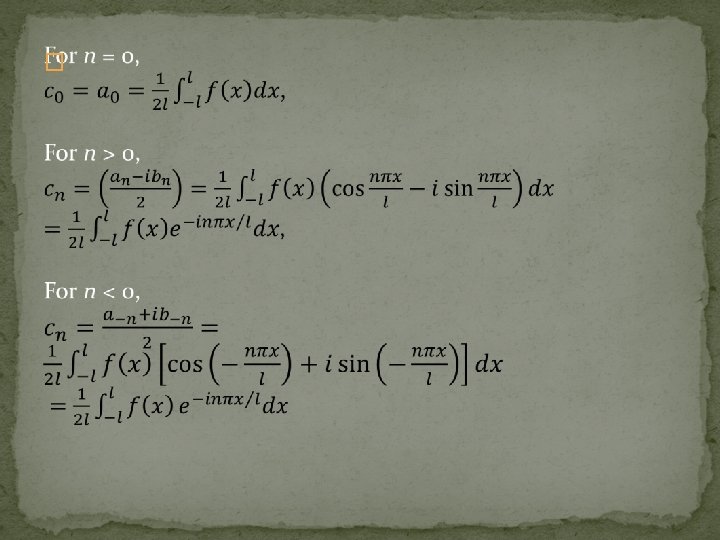

Example: Find the Fourier series for the function defined by Solution: Where Reference: Fourier Analysis (Author: Eric State, Pure and Applied Mathematics: a Wiley-Interscience Series of Texts, Monographs, and Tracts ) P 11
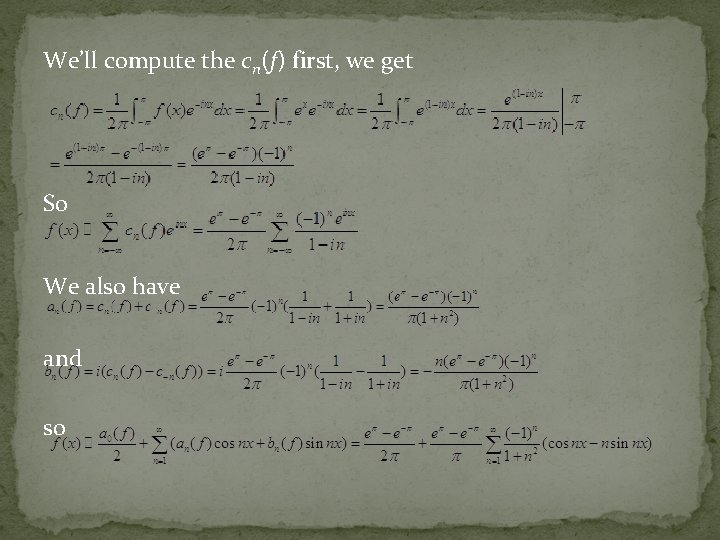
We’ll compute the cn(f) first, we get So We also have and so

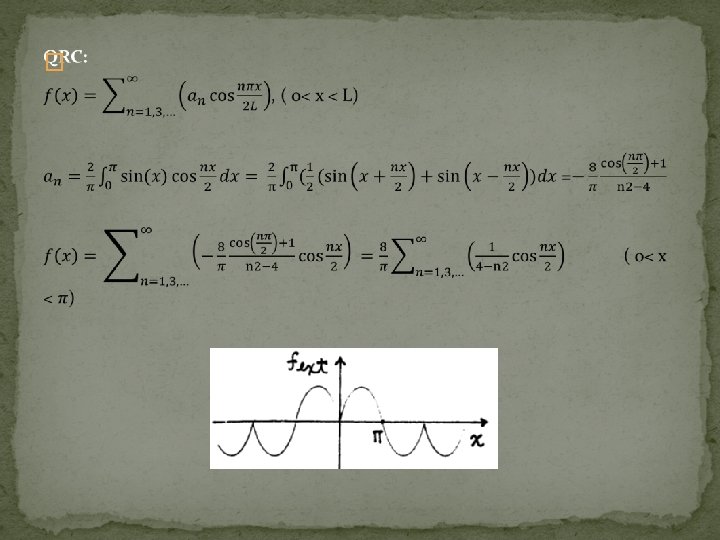
17. 4 Half- and Quarter- Range Expansions It often happens in applications, especially when we solve partial differential equations by the method of separation of variables, that we need to expand a given function f in a Fourier series, where f is defined only on a finite interval. We define an “extended function”, say fext, so that fext is periodic in the domain of -∞< x < ∞, and fext=f(x) on the original interval 0<x<L. There can be infinite number of such extensions. Four extensions: half- and quarter- range cosine and sine extensions, which are based on symmetry or antisymmetry about the endpoints x=0 and x=L.

1. HRC (half range cosines) �
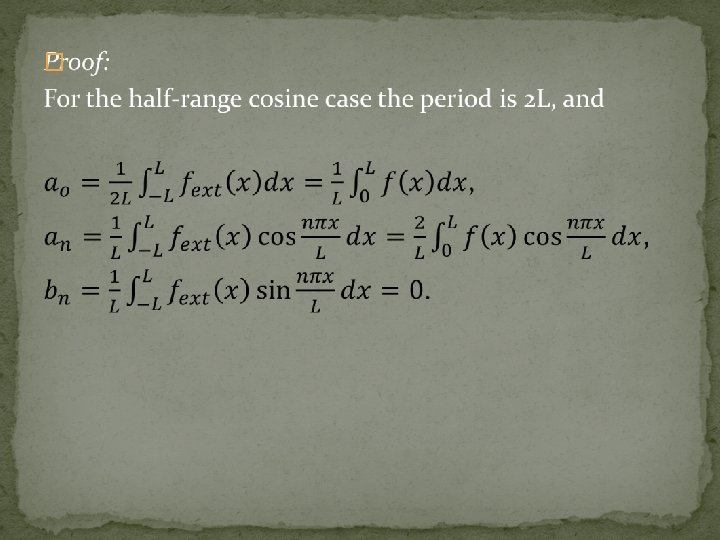

2. HRS (half range sines) �

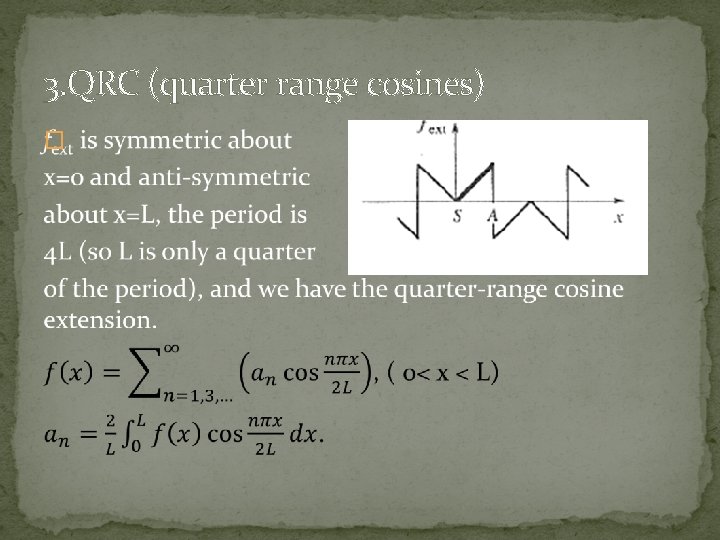
3. QRC (quarter range cosines) �

4. QRS (quarter range sines) �

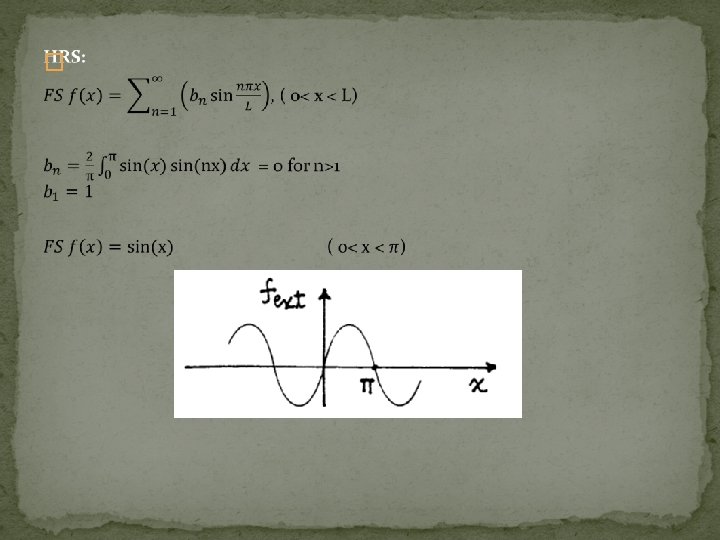

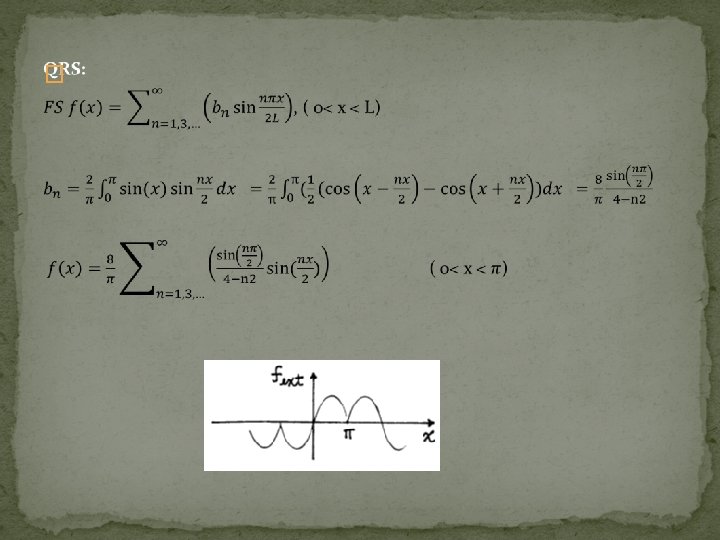

17. 5 Manipulation of Fourier Series Uniform convergence



![17 6 Vector Space Approach Some definitions Function space Cpa b of all 17. 6 Vector Space Approach Some definitions: � Function space. Cp[a, b] of all](https://slidetodoc.com/presentation_image_h/016b7150f349834e79886bfef3b9033d/image-41.jpg)
17. 6 Vector Space Approach Some definitions: � Function space. Cp[a, b] of all real-valued piecewise-continuous functions defined on [a, b]. � f=f(x) and g=g(x) be any two functions in Cp[a, b], and let α be any (real) scalar. f + g ≡f(x) + g(x), αf≡α f(x). Observe that if f and g are piecewise continuous on [a, b] then f+gand αfare also piecewise continuous, so Cp[a, b] is closed under vector addition and scalar multiplication. � We define the zero vector 0 as the function which is identically zero, so that f + 0 = f(x) + 0 = f



So that the normalized en’s are: Thus we can approximate a givenf=f(x), in Cp[a, b], in the form:

Equivalent, we can write

THEOREM 17. 6. 1 Vector Convergence �



THEOREM 17. 7. 1 Sturm-Liouville Theorem �

Example: Solve the Sturn-Liouville problem There a is a constant in the interval (0, 1). Also write down the expansion of an arbitrary element of the appropriate “ ” space in terms of the eigenfunctions of the problem. Solution: We put and So Whose general solution is if not Reference: Fourier Analysis (Author: Eric State, Pure and Applied Mathematics: a Wiley-Interscience Series of Texts, Monographs, and Tracts ) P 224

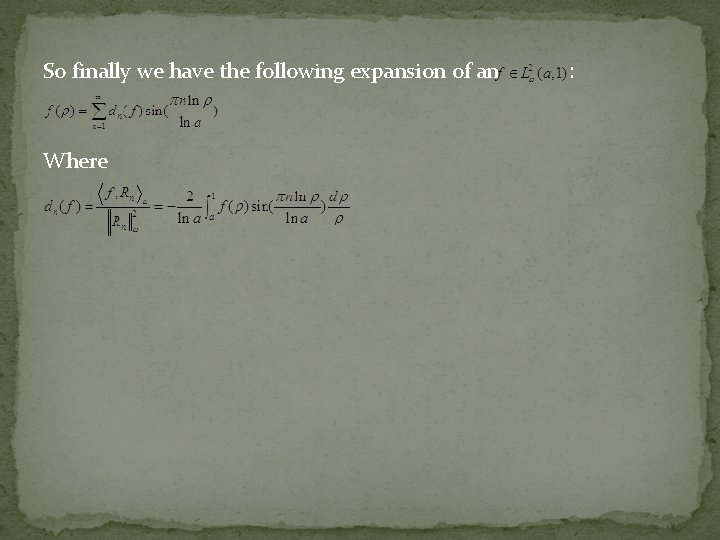
So finally we have the following expansion of an Where :

17. 7. 2 Lagrange identity and proofs Some properties:
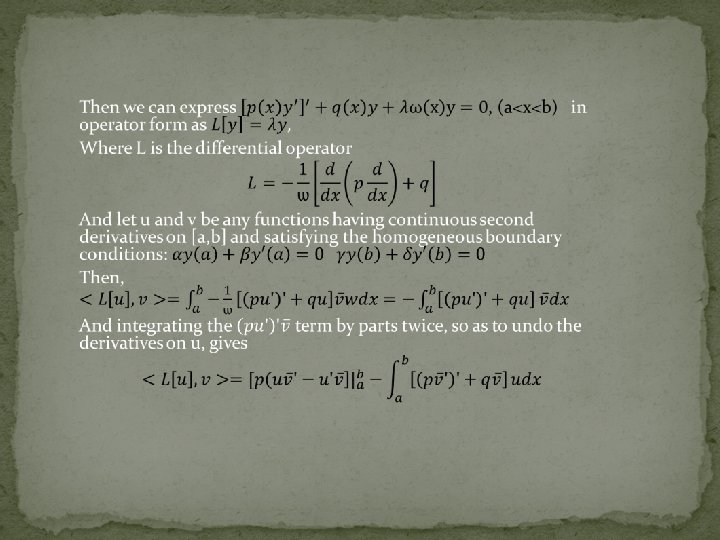


Example: Prove Green’s formla: Since First simplify it as Then So Integrate and get where

17. 8 Periodic and Singular Sturm-Liouville Problems �


THEOREM 17. 8. 1 Periodic and Singular Cases �

Example: Expand , on -1<x<1, in terms of the eigenfunctions of the Sturm-Liouville problem Where y(-1) and y(1) are bounded. According to Section 4. 4, the Legendre equation are bounded on are possible only if for n=0, 1, 2…. , and those nontrivial solutions are the Legendre polynomials Thus, the eigenvalues and eigenfunctions are For n=0, 1, 2… The eigenfunction expansion of a given function f is given by

17. 9 Fourier Integral If a function f defined on -∞< x <∞ is periodic (and sufficiently well-behaved), then it can be represented by a Fourier series. Sometimes we work with functions, defined on -∞< x <∞, that are not periodic, we cannot expand such functions in Fourier series if they are not periodic. Yet, we can think of f as periodic but with an infinite period.


THEOREM 17. 9. 1 Fourier Integral Theorem �

Sine integral function �

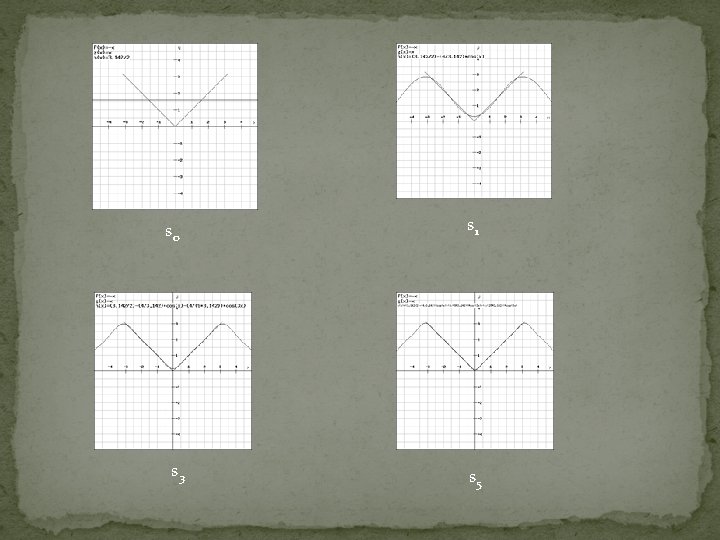
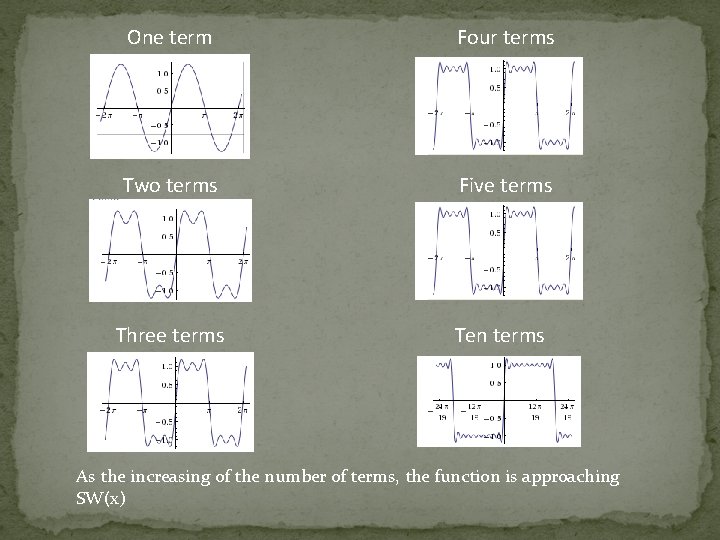
Example: Find the Fourier sine coefficients For k=1, 2, …. between 0 and For w=1, 2, … of the square wave SW(X)

One term Four terms Two terms Five terms Three terms Ten terms As the increasing of the number of terms, the function is approaching SW(x)

17. 10 Fourier Transform �

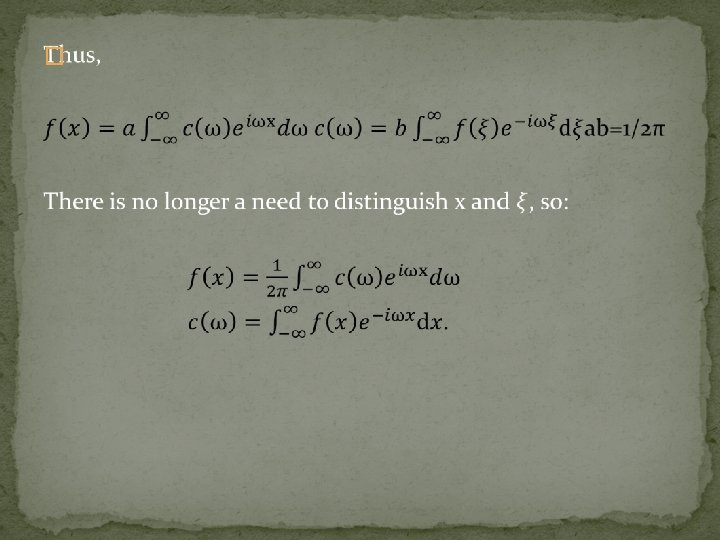

Fourier transform �
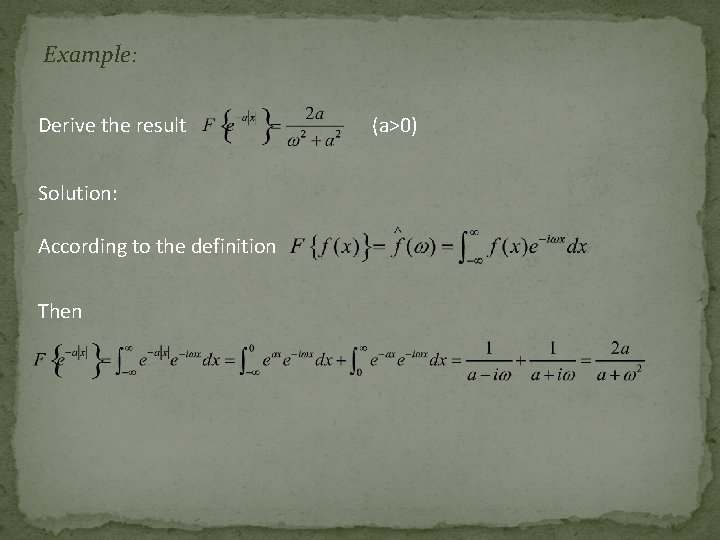
Example: Derive the result Solution: According to the definition Then (a>0)

Properties and applications �


Example: Solve the wave equation and Take the Fourier Transform of both equations. The initial condition gives And the PDE gives Which is basically an ODE in t, we can write it as Which has the solution, and derivative Reference: Steven Bellenot; Fourier Transform Examples http: //www. math. fsu. edu/~bellenot/class/f 09/fun/ft. pdf

So the first initial condition gives and make the solution Let’s first look at Then The second piece and the second gives

And now the first factor looks like an integral, as a derivative with respect to x would cancel the iw in bottom. Define: By fundamental theorem of calculus So Putting both piece together we get the solution



Example: Solve heat transfer equation B. C: (1) u(0, t)=0 (2)u(x, 0)=P(x) Solution with Fourier Sine Transform: According to the B. C, we can get Then Inverse Gives the complete solution or P(x)=1,

Passage from Fourier integral to Laplace transform �

References Greenberg, Advanced Engineering Mathematics 2 nd Edition Jain and Iyengar, Advanced Engineering Mathematics (2007). Jiri Lebl, Differential Equations for Engineers (October 2011). Available at http: //www. jirka. org/diffyqs/.
 Fourier transform
Fourier transform Convert trigonometric fourier series to exponential
Convert trigonometric fourier series to exponential Inverse laplace with complex roots
Inverse laplace with complex roots Convolution theorem
Convolution theorem Integration of dirac delta function
Integration of dirac delta function Z transform ramp function
Z transform ramp function Transform integral
Transform integral Definite integral and indefinite integral
Definite integral and indefinite integral Integral citation
Integral citation Blair matthews
Blair matthews Integral permukaan
Integral permukaan Integral foreign operation
Integral foreign operation Rumus integral
Rumus integral Fourier transform of product of two functions
Fourier transform of product of two functions Delta function fourier transform
Delta function fourier transform Cftft
Cftft Short time fourier transform
Short time fourier transform Fourier transform table
Fourier transform table Parseval's identity for fourier transform
Parseval's identity for fourier transform Duality of fourier transform
Duality of fourier transform Rayleigh energy theorem
Rayleigh energy theorem Phase invariance
Phase invariance Discrete fourier transform of delta function
Discrete fourier transform of delta function Matlab ramp function
Matlab ramp function Mri fourier transform
Mri fourier transform Fourier transform properties examples
Fourier transform properties examples Fourier transform of impulse train
Fourier transform of impulse train Difference of gaussians
Difference of gaussians Fourier transform
Fourier transform Equation of fourier transform
Equation of fourier transform A function
A function Fourier transform
Fourier transform The fourier transform and its applications
The fourier transform and its applications Fourier transform formula
Fourier transform formula Short time fourier transform
Short time fourier transform Fourier transform in polar coordinates
Fourier transform in polar coordinates Fourier transform of product of two functions
Fourier transform of product of two functions 2d discrete fourier transform example
2d discrete fourier transform example Sinc fourier transform
Sinc fourier transform Fourier series of impulse train
Fourier series of impulse train Discrete fourier transform
Discrete fourier transform Fourier transform of impulse train
Fourier transform of impulse train Circ function fourier transform
Circ function fourier transform Duality of fourier transform
Duality of fourier transform Fourier transform is defined for
Fourier transform is defined for Fourier transform of multiplication of two signals
Fourier transform of multiplication of two signals Fourier transform
Fourier transform Fourier transform table
Fourier transform table Fourier integral representation
Fourier integral representation Duality of fourier transform
Duality of fourier transform Fourier sine and cosine series examples
Fourier sine and cosine series examples Windowed fourier transform
Windowed fourier transform Fourier transform
Fourier transform Continuous fourier transform formula
Continuous fourier transform formula Relationship between laplace and fourier transform
Relationship between laplace and fourier transform Introduction to fast fourier transform
Introduction to fast fourier transform Fourier transform solver
Fourier transform solver Series de fourier
Series de fourier What is radix 2 fft
What is radix 2 fft Discrete fourier transform formula
Discrete fourier transform formula Fftshift2
Fftshift2 Chirped pulse fourier transform microwave spectroscopy
Chirped pulse fourier transform microwave spectroscopy Fourier transform of shifted rectangular pulse
Fourier transform of shifted rectangular pulse Dft
Dft Fourier transform pair
Fourier transform pair Fft java
Fft java Top hat function fourier transform
Top hat function fourier transform Inverse of fourier transform
Inverse of fourier transform Fractional fourier transform
Fractional fourier transform Transformata laplace calculator
Transformata laplace calculator Application of discrete fourier transform
Application of discrete fourier transform Fourier transform seismic
Fourier transform seismic Inverse of fourier transform
Inverse of fourier transform Fourier transform computer vision
Fourier transform computer vision Fourier transform complex analysis
Fourier transform complex analysis Ft representation
Ft representation Nstemk
Nstemk Generalized fourier series
Generalized fourier series Fourier transform
Fourier transform Fourier transform
Fourier transform Fourier transform
Fourier transform Fourier
Fourier