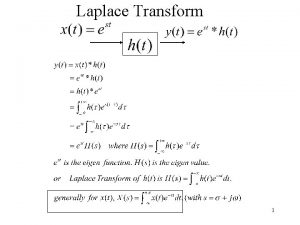Fourier Series The Fourier Transform What is the

Fourier Series & The Fourier Transform What is the Fourier Transform? Anharmonic Waves Fourier Cosine Series for even functions Fourier Sine Series for odd functions The continuous limit: the Fourier transform (and its inverse) Joseph Fourier 1768 -1830 Some transform examples 1

Leerdoelen In dit college behandelen we: • Dat lichtpulsen uit meerdere frequenties bestaan • Ontbinden van een lichtpuls in afzonderlijke golven • Berekenen van het spectrum van een lichtveld: de Fourier transformatie • Voorbeelden en eigenschappen van Fourier transformaties • Fourier transformaties als functie van ruimte: – Hoe ontstaat een brandpunt van een lens – waarom een lichtbundel met een beperkte afmeting altijd meerdere kanten opgaat. Hecht: 7. 3 en 7. 4 2

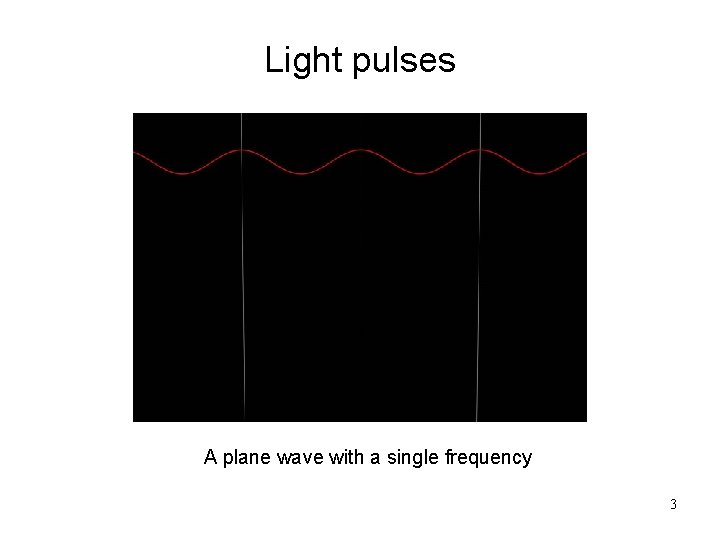
Light pulses A plane wave with a single frequency 3

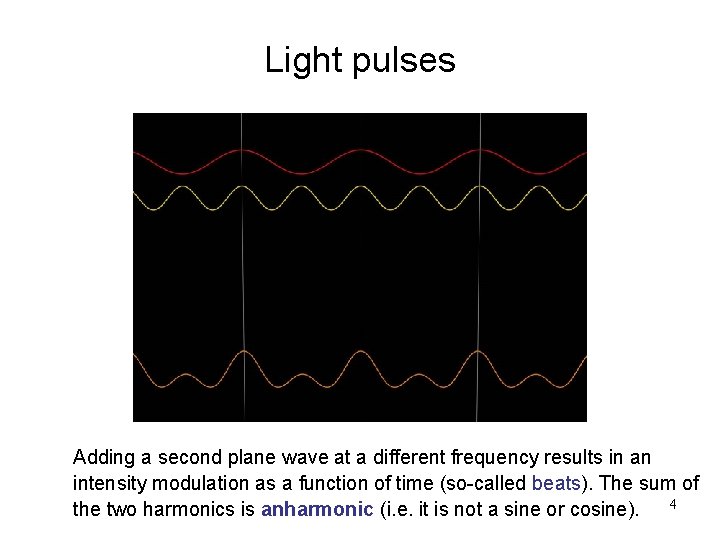
Light pulses Adding a second plane wave at a different frequency results in an intensity modulation as a function of time (so-called beats). The sum of the two harmonics is anharmonic (i. e. it is not a sine or cosine). 4

Light pulses 5

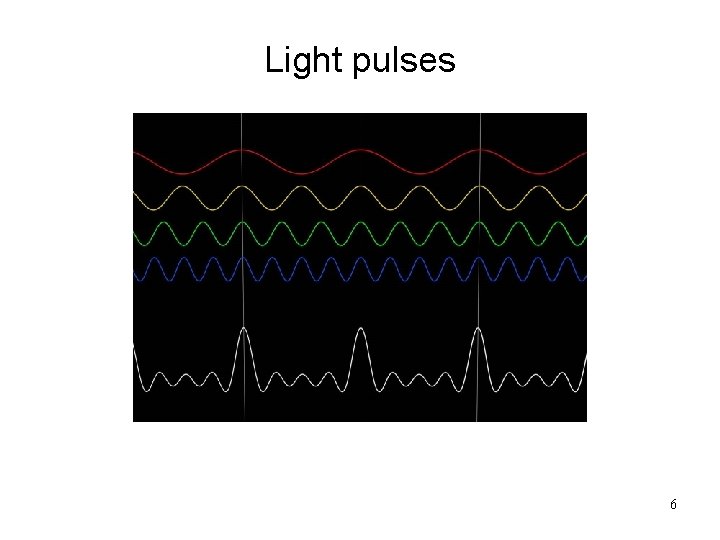
Light pulses 6

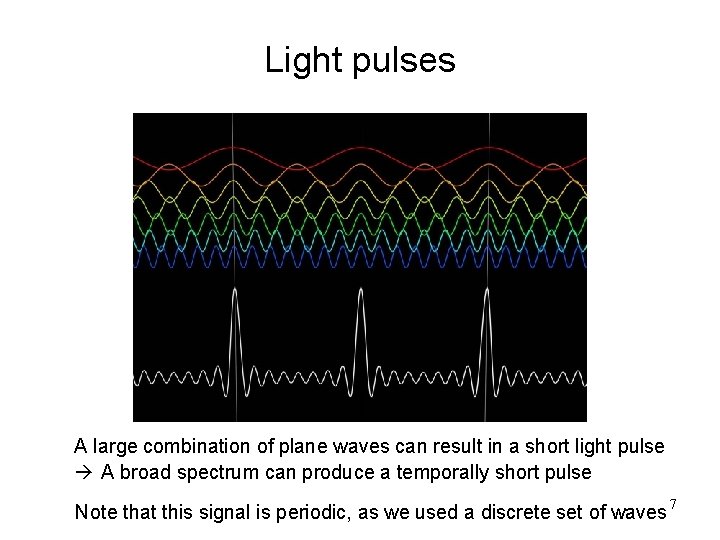
Light pulses A large combination of plane waves can result in a short light pulse à A broad spectrum can produce a temporally short pulse Note that this signal is periodic, as we used a discrete set of waves 7

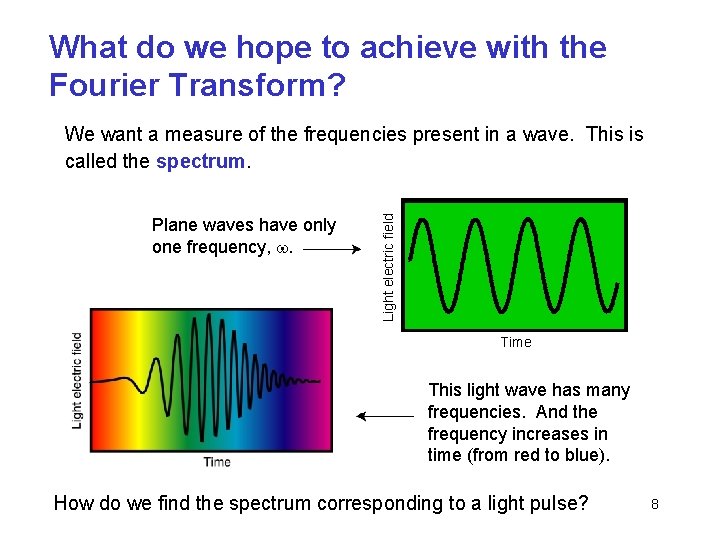
What do we hope to achieve with the Fourier Transform? Plane waves have only one frequency, w. Light electric field We want a measure of the frequencies present in a wave. This is called the spectrum. Time This light wave has many frequencies. And the frequency increases in time (from red to blue). How do we find the spectrum corresponding to a light pulse? 8

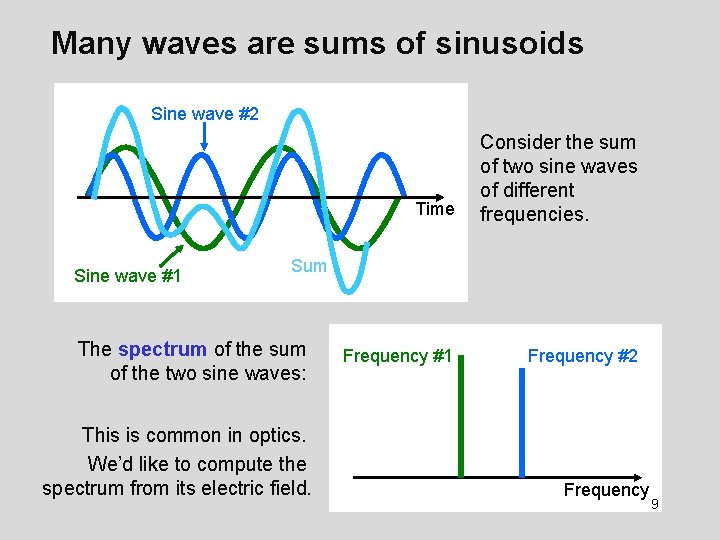
Many waves are sums of sinusoids Sine wave #2 Sine wave #1 Time Consider the sum of two sine waves of different frequencies. Frequency #1 Frequency #2 Sum The spectrum of the sum of the two sine waves: This is common in optics. We’d like to compute the spectrum from its electric field. Frequency 9

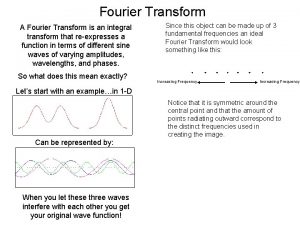
Fourier’s Theorem A function f(x) with spatial periodicity l, can be written as the sum of sines and cosines with wavelengths l , l /2, l /3 etc. Caveat: Fourier’s Theorem holds when the function f (x) is wellbehaved, but we will assume this to be the case. 10

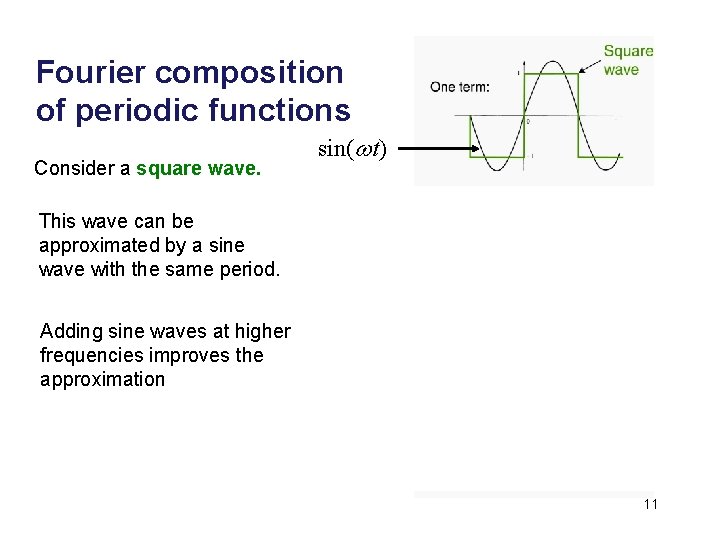
Fourier composition of periodic functions Consider a square wave. This wave can be approximated by a sine wave with the same period. sin(w t) sin(3ωt) Adding sine waves at higher frequencies improves the approximation sin(5ωt) 11

Fourier Sine Series Because sin(mt) is an odd function (for all m), we can write any odd function, f(t), as: where the set {F’m; m = 0, 1, … } is a set of coefficients that specify the strength of each frequency component in the series. We will only worry about the function f(t) over the interval (–π, π) , since the function simply repeats itself outside this interval. 12

Fourier Cosine Series Because cos(mt) is an even function (for all m), we can write any even function, f(t), as: where the set {Fm; m = 0, 1, … } is a set of coefficients that specify the strength of each frequency component in the series. Again, we will only worry about the function f(t) over the interval (–π, π), since the function simply repeats itself outside this interval. 13

Any function can be written as the sum of an even and an odd function E(-x) = E(x) O(-x) = -O(x) 14

Proof We begin by assuming that this proposition is true, and then we calculate E(x) and O(x): We then also have that Adding (1) and (2) gives Subtracting (1) and (2) gives 15

Fourier Series So if f(t) is a general periodic function, neither even nor odd, it can be written: even component odd component where and 16

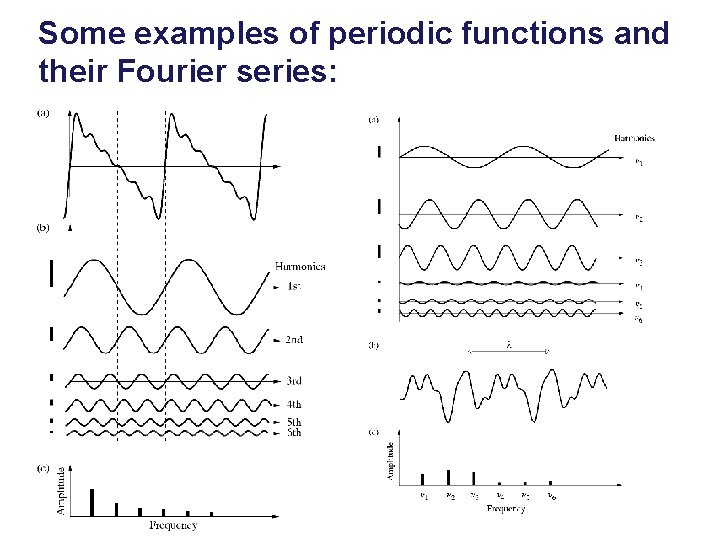
Some examples of periodic functions and their Fourier series: 17

Finding the coefficients, Fm, in a Fourier Cosine Series The strength of an individual Fourier component can be calculated as: Here is the formal proof: 18

Finding the coefficients, Fm, in a Fourier Sine Series The strength of an individual Fourier component can be calculated as: And the proof works exactly the same as for the cosine series. 19

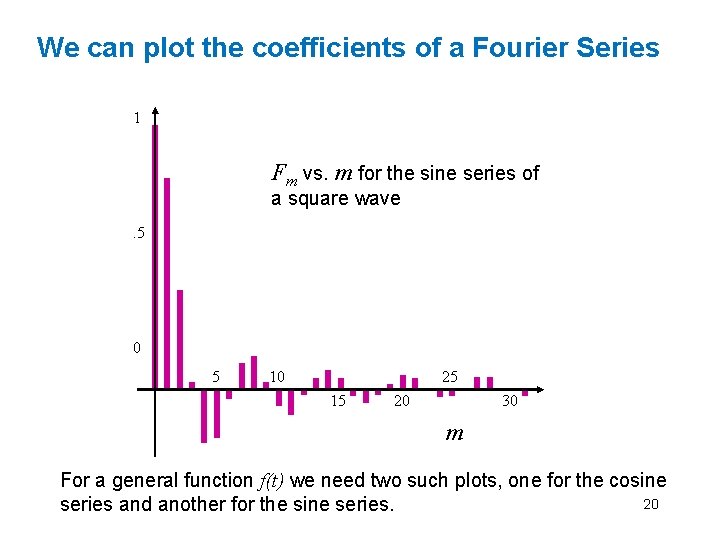
We can plot the coefficients of a Fourier Series 1 Fm vs. m for the sine series of a square wave. 5 0 5 10 25 15 20 30 m For a general function f(t) we need two such plots, one for the cosine 20 series and another for the sine series.

The Discrete Fourier Transform Consider the Fourier coefficients. You can define a complex function F(m) that combines the cosine and sine series coefficients: Fm” Fm – i F‘m We use the Discrete Fourier Transform when we only have discrete measurements of f(t): Because f(t) is periodic (or only defined on the interval (–π, π) ), the ‘frequency’ m only takes integer values. 21

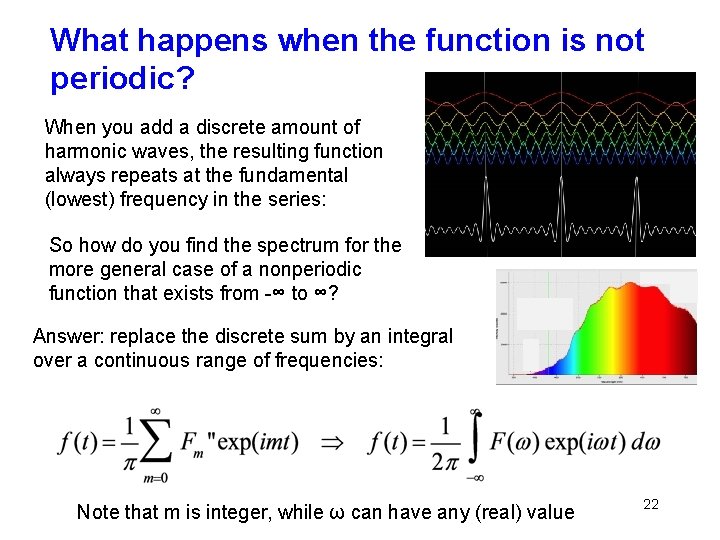
What happens when the function is not periodic? When you add a discrete amount of harmonic waves, the resulting function always repeats at the fundamental (lowest) frequency in the series: So how do you find the spectrum for the more general case of a nonperiodic function that exists from -∞ to ∞? Answer: replace the discrete sum by an integral over a continuous range of frequencies: Note that m is integer, while ω can have any (real) value 22

The Fourier Transform This transformation is called the Fourier Transform: Fourier Transform Inverse Fourier Transform These transformations allow you to calculate the frequency dependence F(ω) of a time domain function f(t), and vice versa. There are different definitions of these transforms. The 2π can occur in several places, but the idea is generally the same. 23

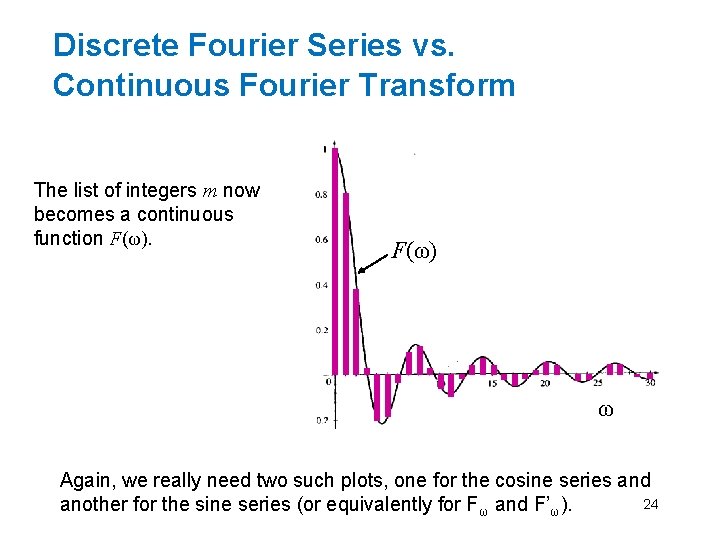
Discrete Fourier Series vs. Continuous Fourier Transform The list of integers m now becomes a continuous function F(ω) ω Again, we really need two such plots, one for the cosine series and 24 another for the sine series (or equivalently for Fω and F’ω).

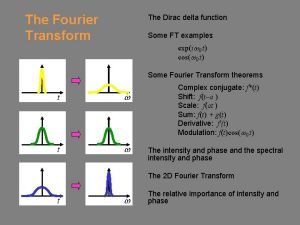
Fourier Transform Notation There are several ways to denote the Fourier transform of a function. If the function is labeled by a lower-case letter, such as f, we can write: If the function is already labeled by an upper-case letter, such as E, we can write: or: � ∩ Sometimes, this symbol is used instead of the arrow: 25

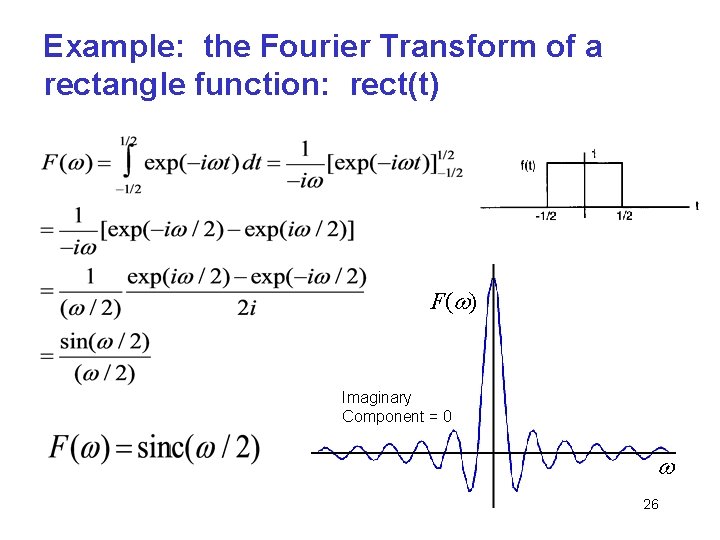
Example: the Fourier Transform of a rectangle function: rect(t) F(w) Imaginary Component = 0 w 26

The link to optical waves and spectra Up to now we have described the Fourier transform in general terms. Of course, these can be applied to the electric field of light E(t). We define the spectrum, S(ω), of a light field E(t) to be: This is the measure of the frequencies present in a light field. 27

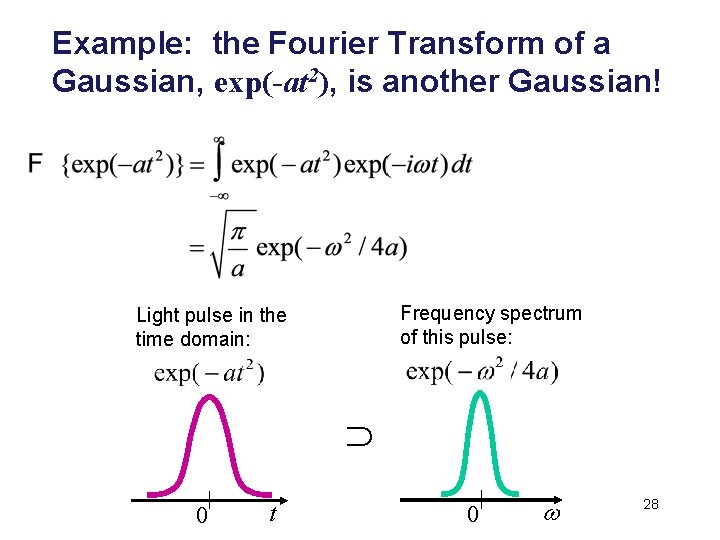
Example: the Fourier Transform of a Gaussian, exp(-at 2), is another Gaussian! Frequency spectrum of this pulse: Light pulse in the time domain: ∩ 0 t 0 w 28

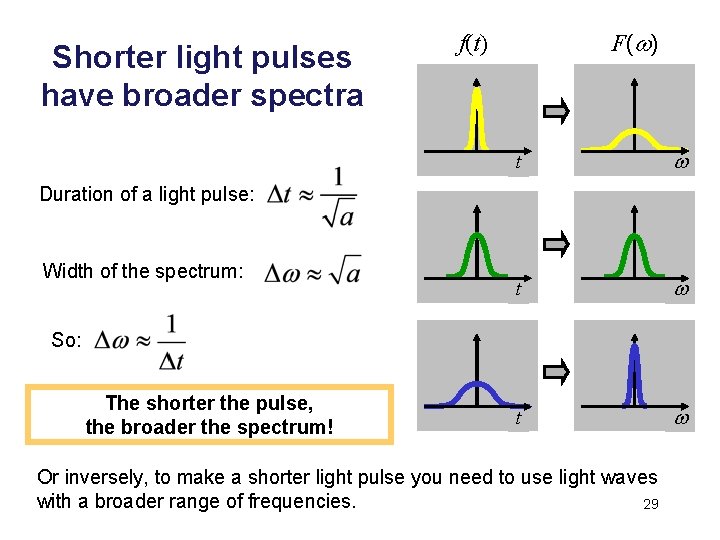
Shorter light pulses have broader spectra F(w) f(t) t w t w Duration of a light pulse: Width of the spectrum: So: The shorter the pulse, the broader the spectrum! Or inversely, to make a shorter light pulse you need to use light waves with a broader range of frequencies. 29

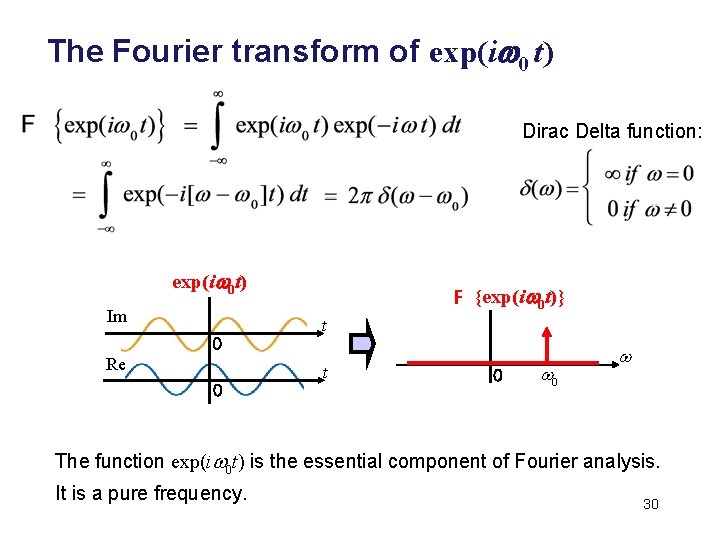
The Fourier transform of exp(iw 0 t) Dirac Delta function: exp(iw 0 t) Im 0 Re 0 F {exp(iw 0 t)} t t 0 w 0 w The function exp(iw 0 t) is the essential component of Fourier analysis. It is a pure frequency. 30

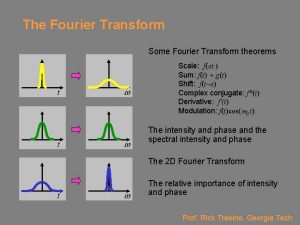
Some properties of Fourier transforms Addition of Fourier transforms: Scale theorem: Fourier shift theorem: Complex conjugate: Fourier transform of a derivative: 31

Some functions don’t have Fourier transforms. The condition for the existence of a given F(w) is: Functions that do not asymptotically go to zero for large values of |t|, generally do not have Fourier transforms. So we’ll assume that all functions of interest go to zero at ±∞. 32

Fourier Transform with Respect to Space Certain objects are periodic in space, for example crystals, or the street pattern of Manhattan. f(x) If f(x) is a function of position x, we can define a spatial Fourier transform: F {f(x)} = F(k) We refer to k as the spatial frequency. x F(k) k Everything we’ve said about Fourier transforms between the t and w domains also applies to the x and k domains. 33

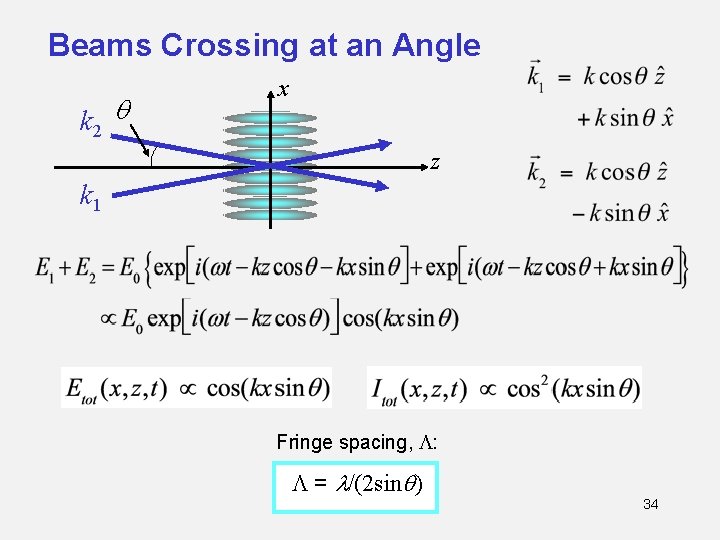
Beams Crossing at an Angle k 2 q x z k 1 Fringe spacing, L: L = l/(2 sinq) 34

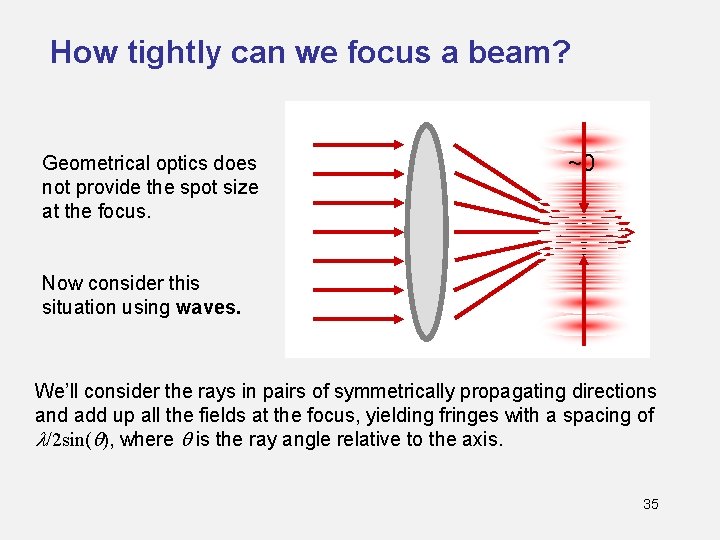
How tightly can we focus a beam? Geometrical optics does not provide the spot size at the focus. ~0 Now consider this situation using waves. We’ll consider the rays in pairs of symmetrically propagating directions and add up all the fields at the focus, yielding fringes with a spacing of l/2 sin(q), where q is the ray angle relative to the axis. 35

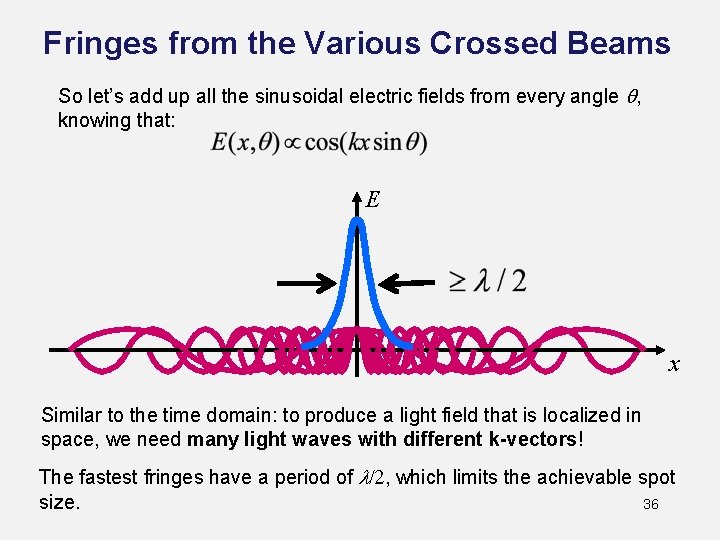
Fringes from the Various Crossed Beams So let’s add up all the sinusoidal electric fields from every angle q, knowing that: E x Similar to the time domain: to produce a light field that is localized in space, we need many light waves with different k-vectors! The fastest fringes have a period of l/2, which limits the achievable spot size. 36

Tot slot Wat hebben we gezien: • Fourier reeksen en Fourier transformaties! • Het nut hiervan: omrekenen van tijd naar frequentie en andersom • Eigenschappen van Fourier transformaties • Fourier transformatie van een korte lichtpuls • Hoe een focus ontstaat: optellen van golven met verschillende hoeken. 37