The heat equation Fourier and CrankNicolsen Repetition and









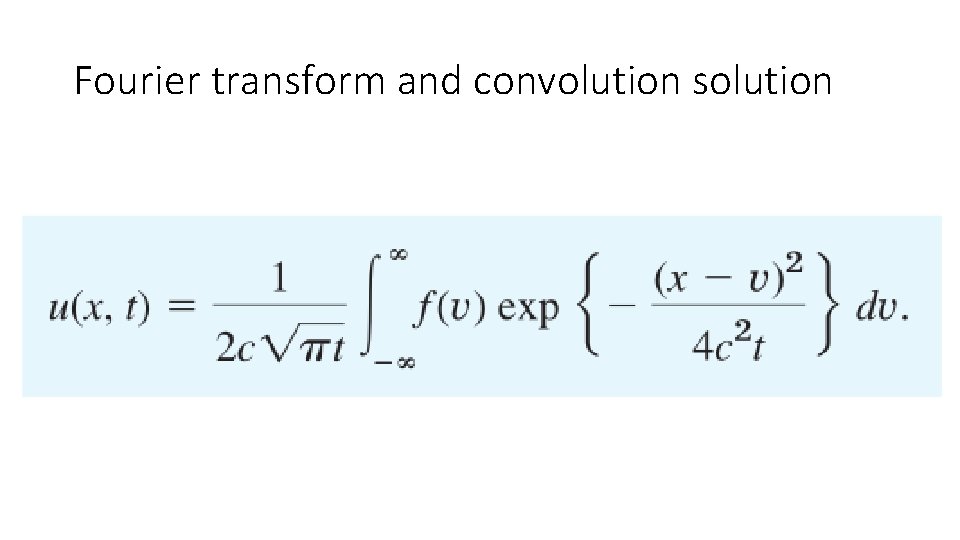







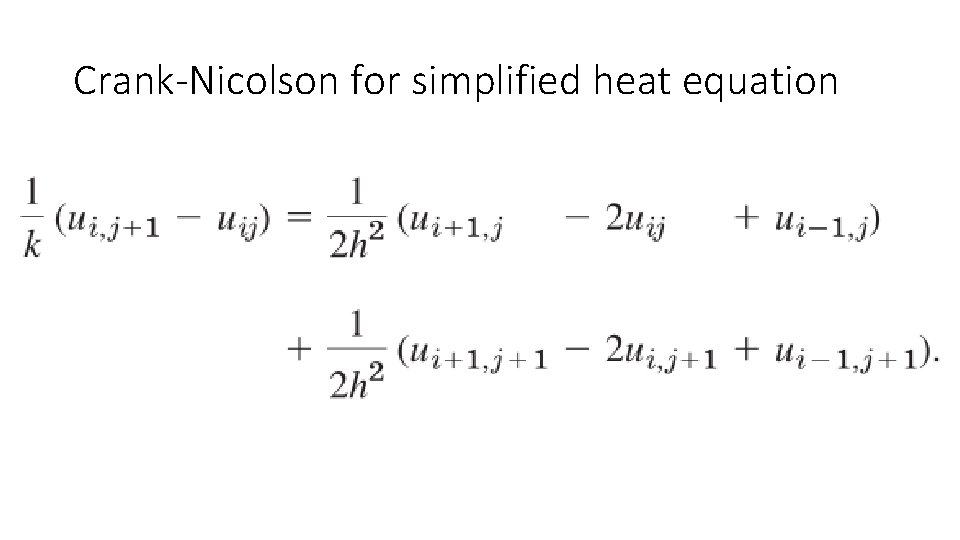



- Slides: 28

The heat equation Fourier and Crank-Nicolsen Repetition and additional notes

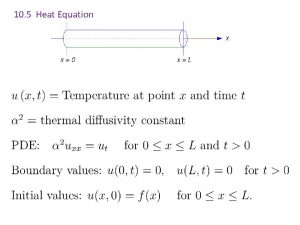
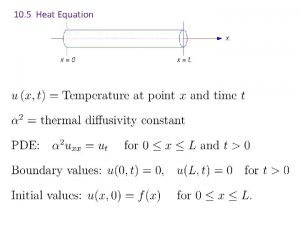
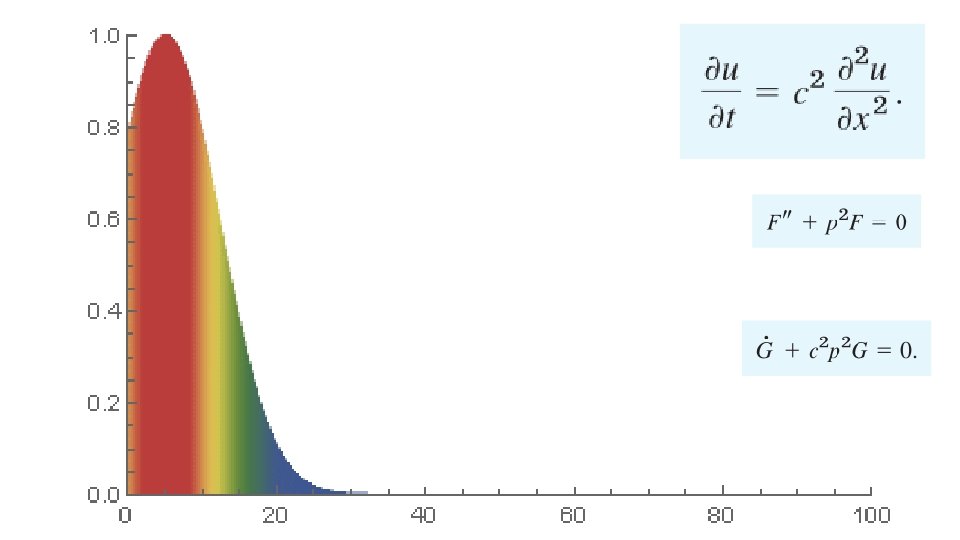
Solutions of the heat equation smooths out Suppose one has a function u that describes the temperature at a given location (x, y, z). This function will change over time as heat spreads throughout space. The heat equation is used to determine the change in the function u over time. The rate of change of u is proportional to the "curvature" of u. Thus, the sharper the corner, the faster it is rounded off. Over time, the tendency is for peaks to be eroded, and valleys filled in. If u is linear in space (or has a constant gradient) at a given point, then u has reached steady-state and is unchanging at this point (assuming a constant thermal conductivity).


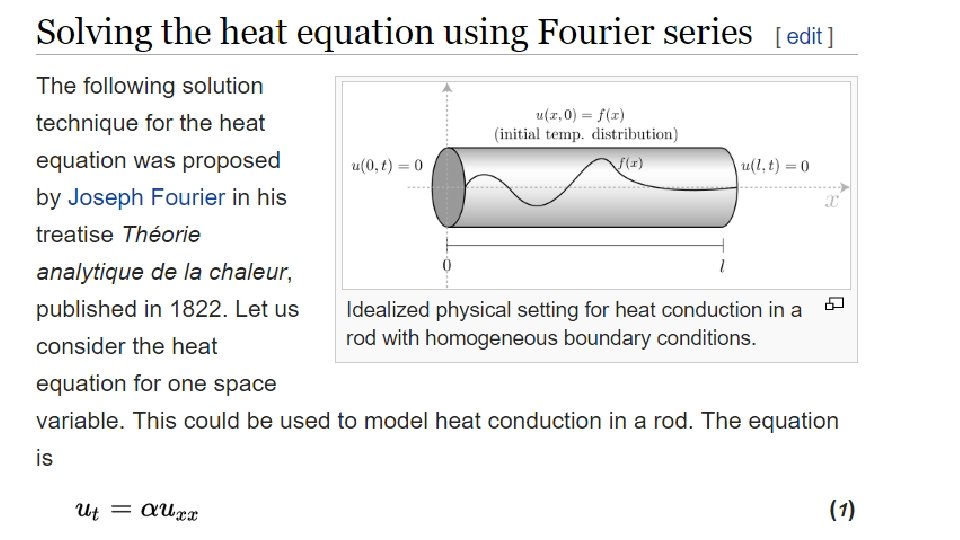
Wikipedia on Fourier series (2016) Fourier introduced the series for the purpose of solving the heat equation in a metal plate, publishing his initial results in his 1807 Mémoire sur la propagation de la chaleur dans les corps solides (Treatise on the propagation of heat in solid bodies), and publishing his Théorie analytique de la chaleur (Analytical theory of heat) in 1822. Early ideas of decomposing a periodic function into the sum of simple oscillating functions date back to the 3 rd century BC, when ancient astronomers proposed an empiric model of planetary motions, based on deferents and epicycles.


Fourier: Analytical theory of heat (1822)



Heat and diffusion equations correspond to conservation of energy and mass respectively

There are many applications The heat equation is of fundamental importance in diverse scientific fields. In mathematics, it is the prototypical parabolic partial differential equation. In probability theory, the heat equation is connected with the study of Brownian motion via the Fokker–Planck equation. In financial mathematics it is used to solve the Black– Scholes partial differential equation. The diffusion equation, a more general version of the heat equation, arises in connection with the study of chemical diffusion and other related processes. …. The wave equation can be approximately solved by the so-called parabolic approximation which gives a similar equation.

Medisinsk ultralyd 2010 ? ? (written in year 2000) http: //www. cs. unc. edu/~us/

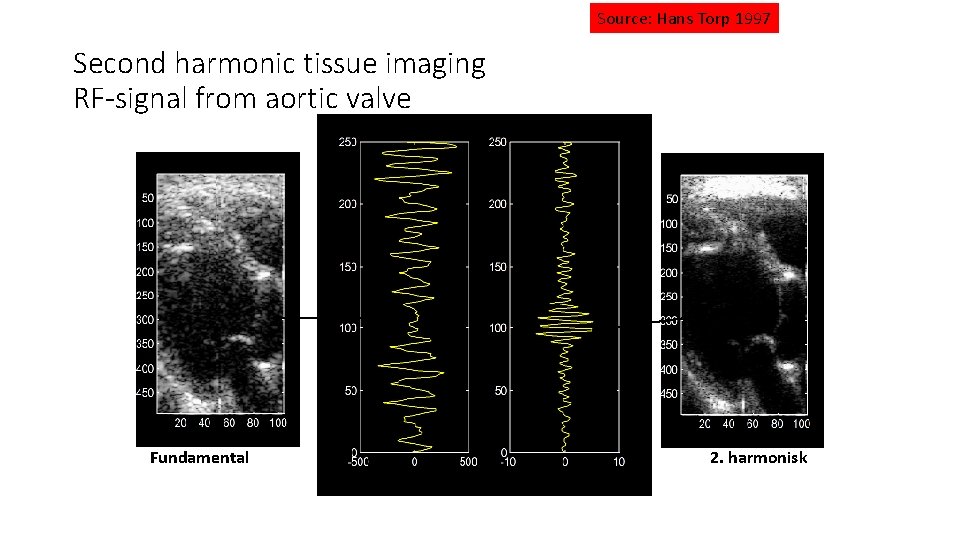
Source: Hans Torp 1997 Second harmonic tissue imaging RF-signal from aortic valve Fundamental 2. harmonisk

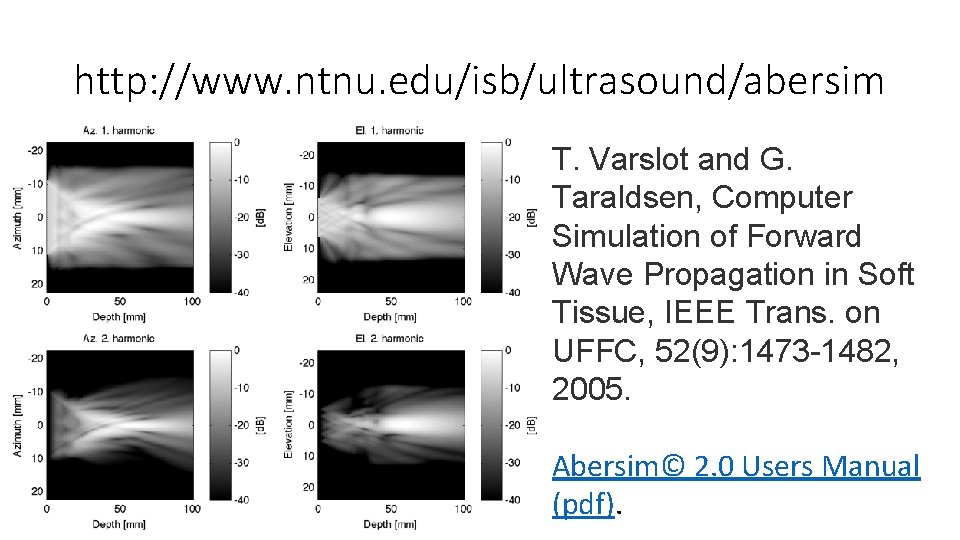
http: //www. ntnu. edu/isb/ultrasound/abersim T. Varslot and G. Taraldsen, Computer Simulation of Forward Wave Propagation in Soft Tissue, IEEE Trans. on UFFC, 52(9): 1473 -1482, 2005. Abersim© 2. 0 Users Manual (pdf).
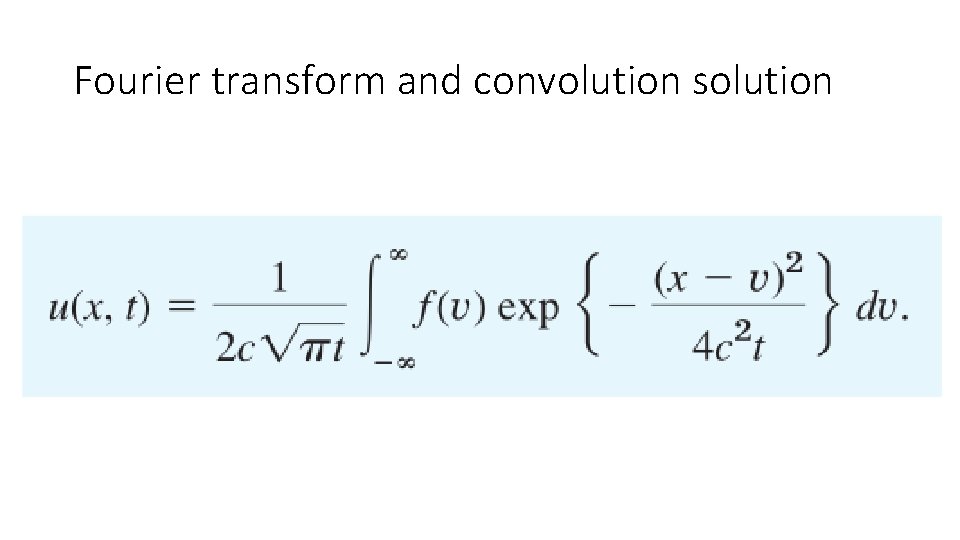
Fourier transform and convolution solution


Numerical solution Finally …. Crank-Nicolson = trapezoidal rule


Wikipedia (2016) on Crank-Nicolson For diffusion equations (and many other equations), it can be shown the Crank–Nicolson method is unconditionally stable. [3] However, the approximate solutions can still contain (decaying) spurious oscillations if the ratio of time step Δt times thermal diffusivity to the square of space step, Δx 2, is large (typically larger than 1/2 per Von Neumann stability analysis). For this reason, whenever large time steps or high spatial resolution is necessary, the less accurate backward Euler method is often used, which is both stable and immune to oscillations.

ODE solvers for 1 d heat-equation relatives

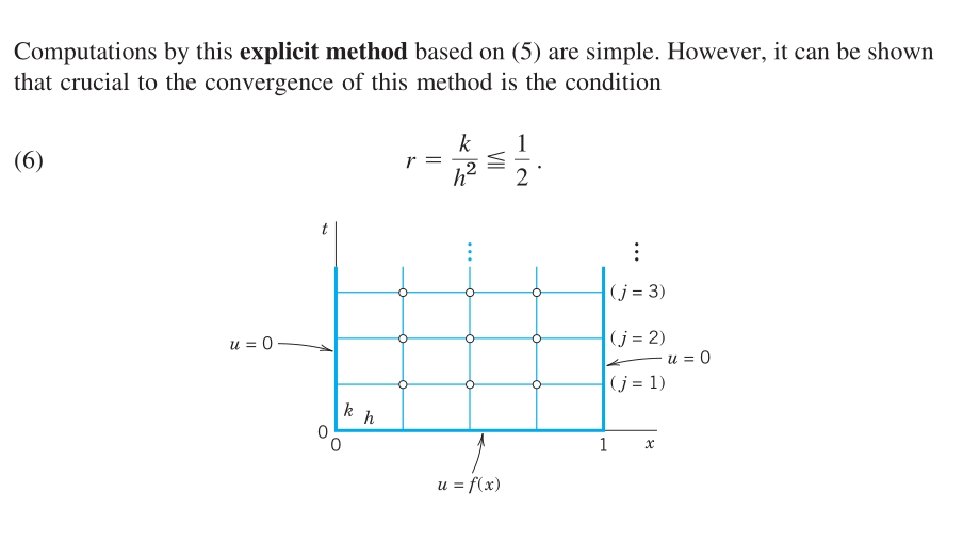
Simplified heat equation


Physical interpretation and numerics

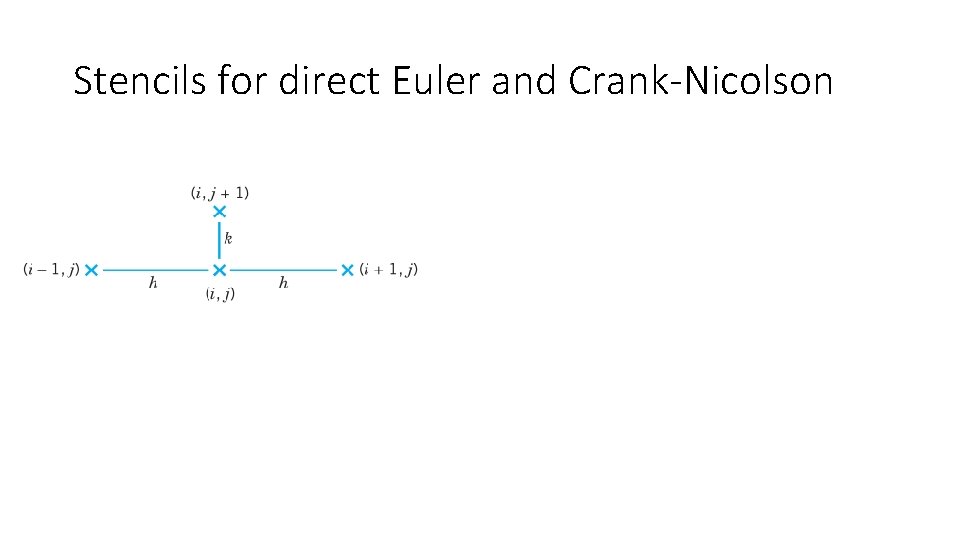
Stencils for direct Euler and Crank-Nicolson
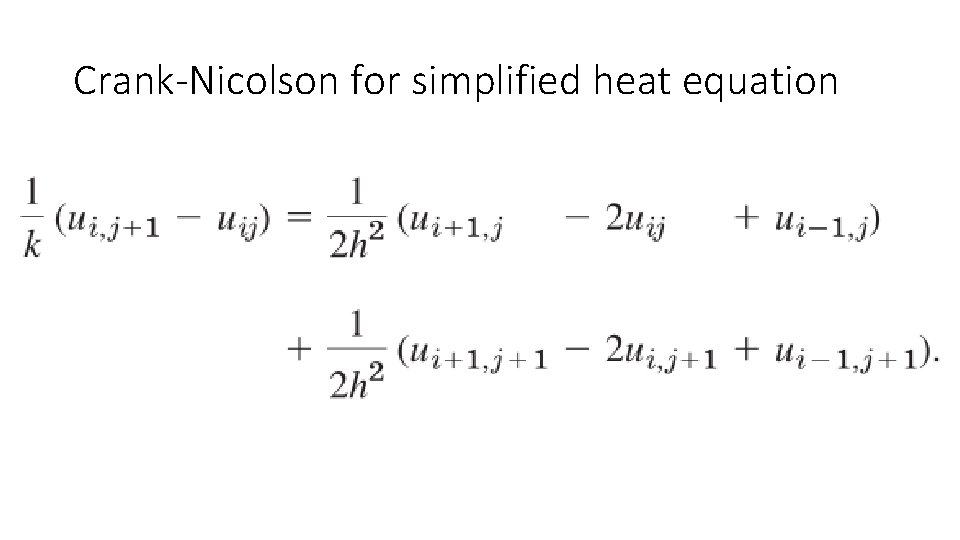
Crank-Nicolson for simplified heat equation


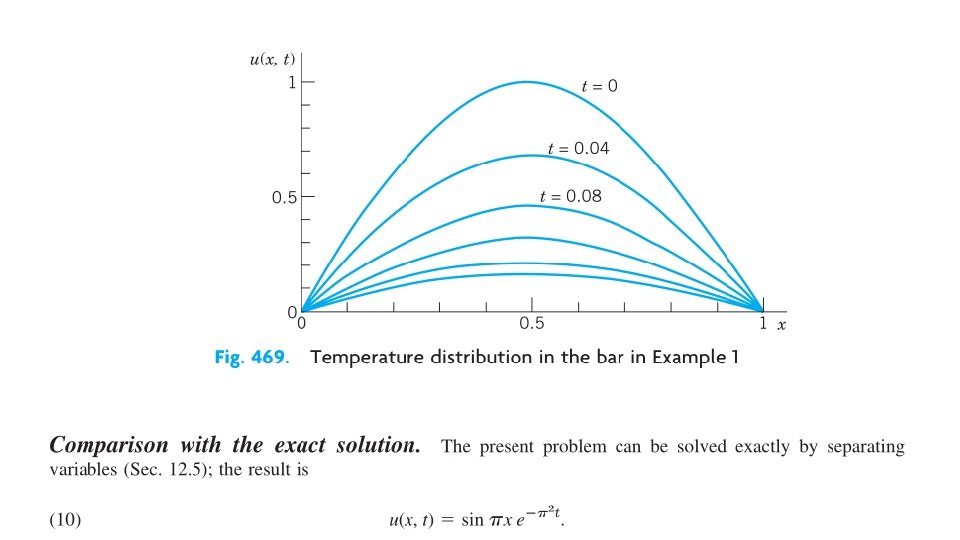
We have to perform 4 times as many steps as with the Crank– Nicolson


The End
 Heat equation
Heat equation Example of bandwagon propaganda
Example of bandwagon propaganda Radial heat conduction
Radial heat conduction What is law of heat exchange
What is law of heat exchange Fourier's law of heat conduction
Fourier's law of heat conduction Fourier transform of 1
Fourier transform of 1 Bn formula in fourier series
Bn formula in fourier series Rayleigh energy theorem
Rayleigh energy theorem What is the formula for latent heat
What is the formula for latent heat Specific heat capacity graph
Specific heat capacity graph Moist heat examples
Moist heat examples Enthalpy equation with specific heat
Enthalpy equation with specific heat Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Ng-html
Ng-html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Gấu đi như thế nào
Gấu đi như thế nào Chụp tư thế worms-breton
Chụp tư thế worms-breton Alleluia hat len nguoi oi
Alleluia hat len nguoi oi Các môn thể thao bắt đầu bằng tiếng nhảy
Các môn thể thao bắt đầu bằng tiếng nhảy Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Công thức tiính động năng
Công thức tiính động năng Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân Làm thế nào để 102-1=99
Làm thế nào để 102-1=99 độ dài liên kết
độ dài liên kết Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật