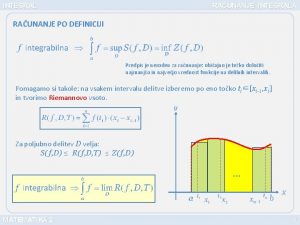
TRANSFORMATA FOURIER INTEGRALA FOURIER TRANSFORMATA FOURIER INVERS FORME



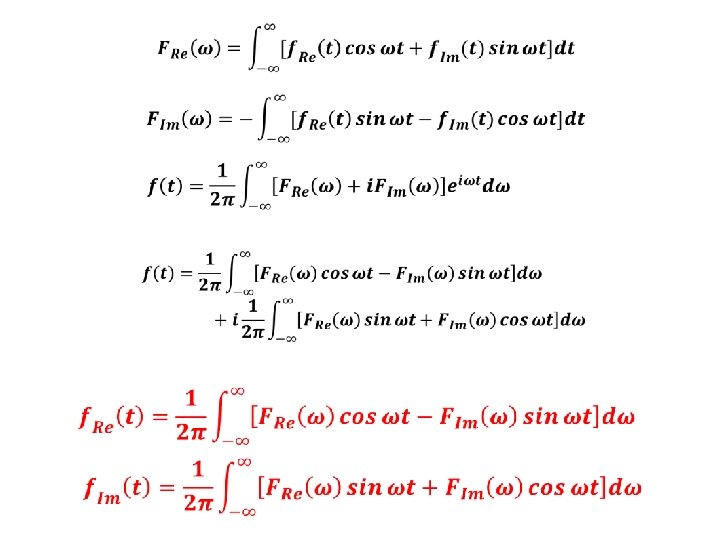





















- Slides: 33

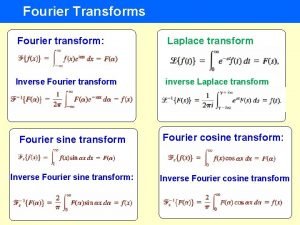
TRANSFORMATA FOURIER (INTEGRALA FOURIER)

TRANSFORMATA FOURIER INVERSĂ

FORME SPECIALE TRANSFORMATEI FOURIER CAZUL FUNCŢIILOR COMPLEXE substituind obţinem şi, utilizând identitatea Euler,
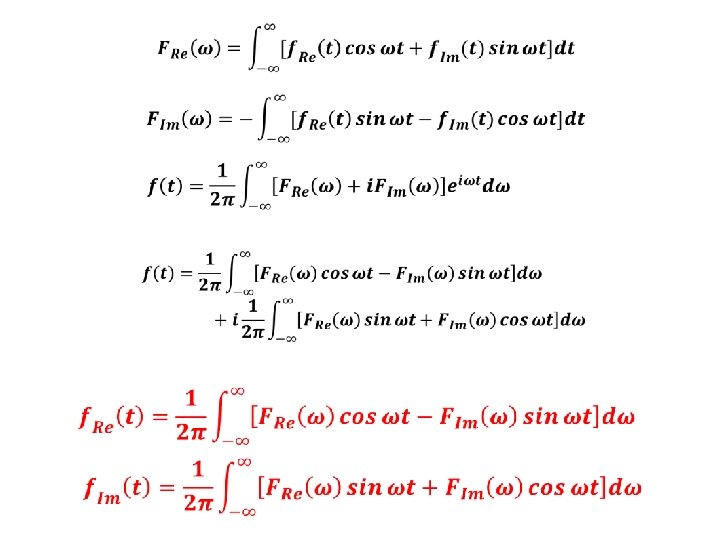

CAZUL FUNCŢIILOR REALE Dacă f(t) este reală, F(ω) este (în general) complexă Deoarece orice funcţie f(t) poate fi exprimată ca o sumă dintre o funcţie pară şi o funcţie impară, vom considera separat cazurile în care funcţia f(t) este reală şi pară, respectiv reală şi impară

funcţia cos este pară funcţia sin este impară produsul dintre două funcţii impare este o funcţie pară produsul dintre două funcţii pare este o funcţie pară produsul dintre o funcţie impară şi o funcţie pară este o funcţie impară

Cazul în care f(t) este reală şi pară impară Deci: Pentru a determina dacă F(ω) este pară sau impară, calculăm CONCLUZIE: Dacă f(t) este reală şi pară, F(ω) este reală şi pară

Cazul în care f(t) este reală şi impară Deci: imaginară Pentru a determina dacă F(ω) este pară sau impară, calculăm CONCLUZIE: Dacă f(t) este reală şi impară, F(ω) este imaginară şi impară

CAZUL FUNCŢIILOR IMAGINARE Dacă f(t) este imaginară, F(ω) este (în general) complexă Deoarece orice funcţie f(t) poate fi exprimată ca o sumă dintre o funcţie pară şi o funcţie impară, vom considera separat cazurile în care funcţia f(t) este imaginară şi pară, respectiv imaginară şi impară

Cazul în care f(t) este imaginară şi pară impară Deci: imaginară Pentru a determina dacă F(ω) este pară sau impară, calculăm CONCLUZIE: Dacă f(t) este imaginară şi pară, F(ω) este imaginară şi pară

Cazul în care f(t) este imaginară şi impară Deci: imaginară Pentru a determina dacă F(ω) este pară sau impară, calculăm CONCLUZIE: Dacă f(t) este imaginară şi impară, F(ω) este reală şi impară

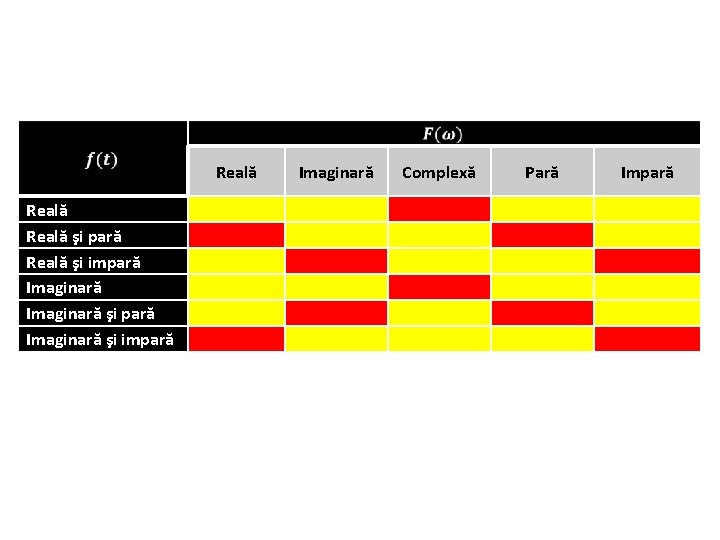
Reală şi pară Reală şi impară Imaginară şi impară Reală Imaginară Complexă Pară Impară

PROPRIETĂŢI ŞI TEOREME Liniaritatea Simetria Scalarea în domeniul timp

Deplasarea în domeniul timpului Deplasarea în domeniul frecvenţei

Derivarea în domeniul timpului Derivarea în domeniul frecvenţei Integrarea în domeniul timpului

Valorile conjugate în timp şi complex Convoluţia în domeniul timpului Convoluţia în domeniul frecvenţei

Aria de sub f(t) Aria de sub F(ω) Teorema lui Parseval

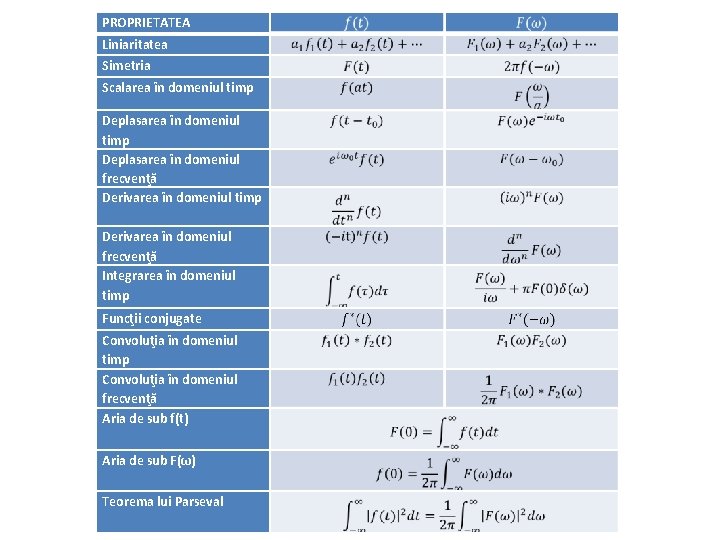
PROPRIETATEA Liniaritatea Simetria Scalarea în domeniul timp Deplasarea în domeniul frecvenţă Derivarea în domeniul timp Derivarea în domeniul frecvenţă Integrarea în domeniul timp Funcţii conjugate Convoluţia în domeniul timp Convoluţia în domeniul frecvenţă Aria de sub f(t) Aria de sub F(ω) Teorema lui Parseval

TRANSFORMATA FOURIER A CELOR MAI IMPORTANTE FUNCŢII Funcţia delta Teorema deplasării în timp

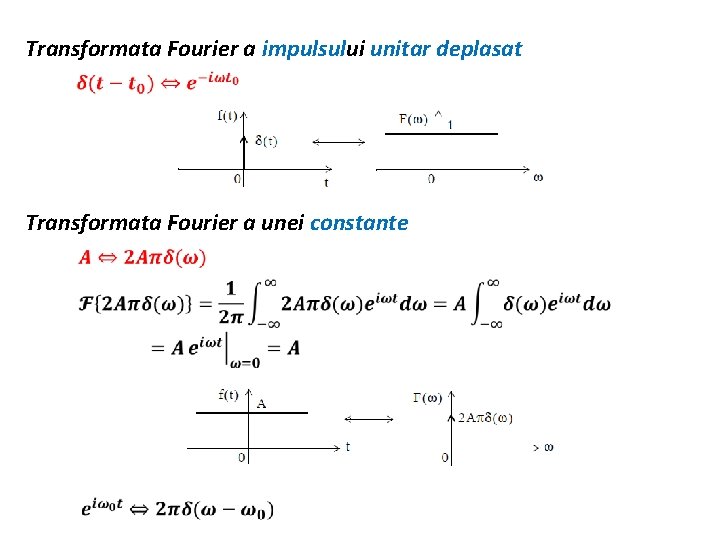
Transformata Fourier a impulsului unitar deplasat Transformata Fourier a unei constante

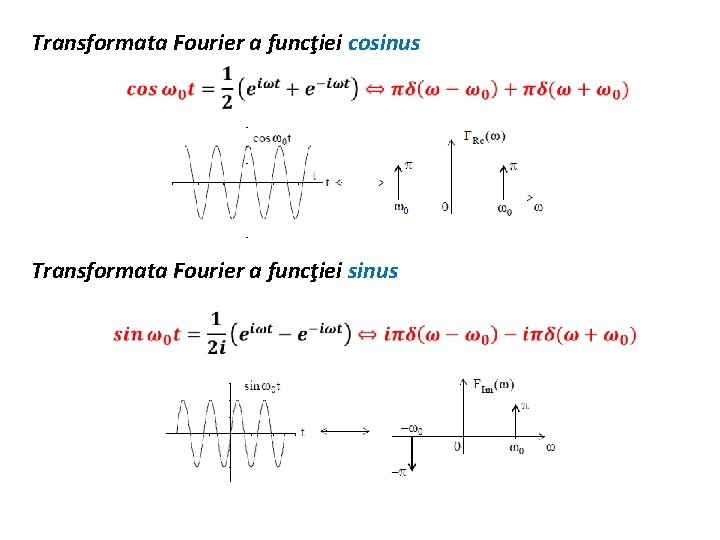
Transformata Fourier a funcţiei cosinus Transformata Fourier a funcţiei sinus

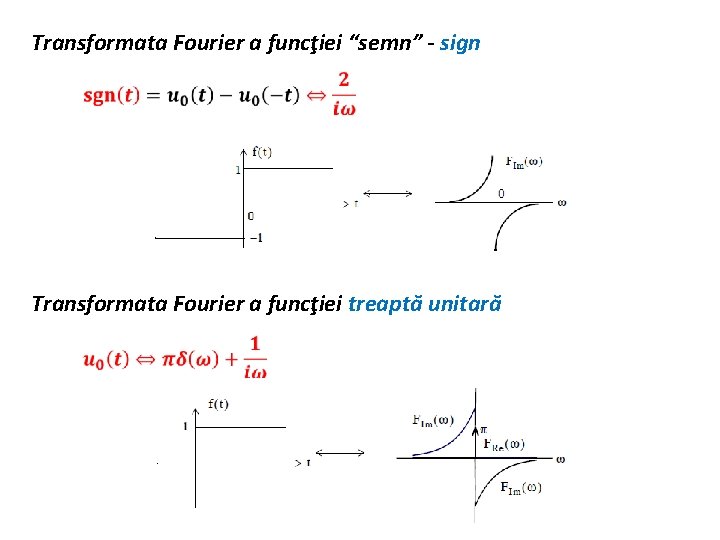
Transformata Fourier a funcţiei “semn” - sign Transformata Fourier a funcţiei treaptă unitară

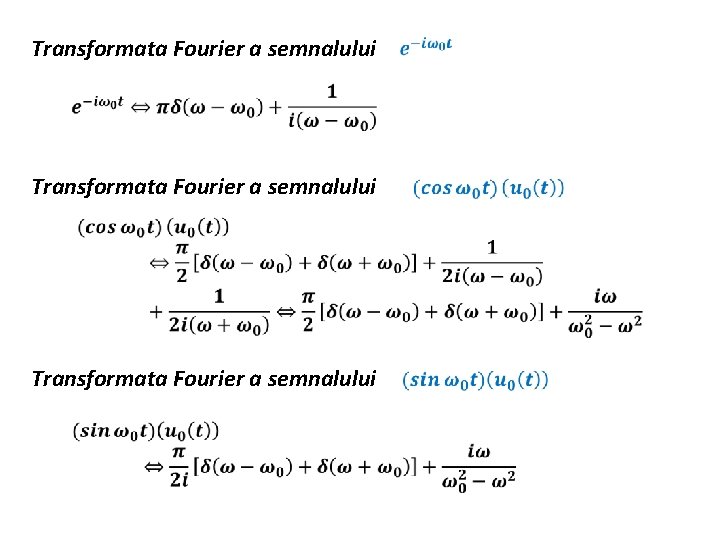
Transformata Fourier a semnalului


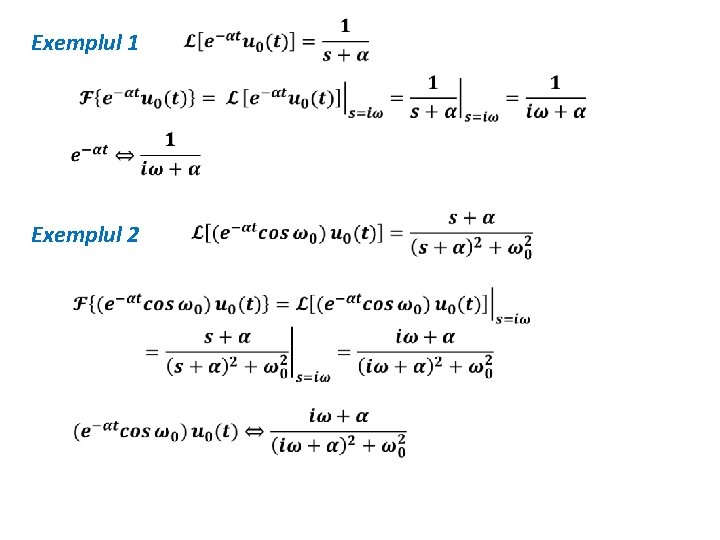
DEDUCEREA TRANSFORMATEI FOURIER DIN TRANSFORMATA LAPLACE

Exemplul 1 Exemplul 2

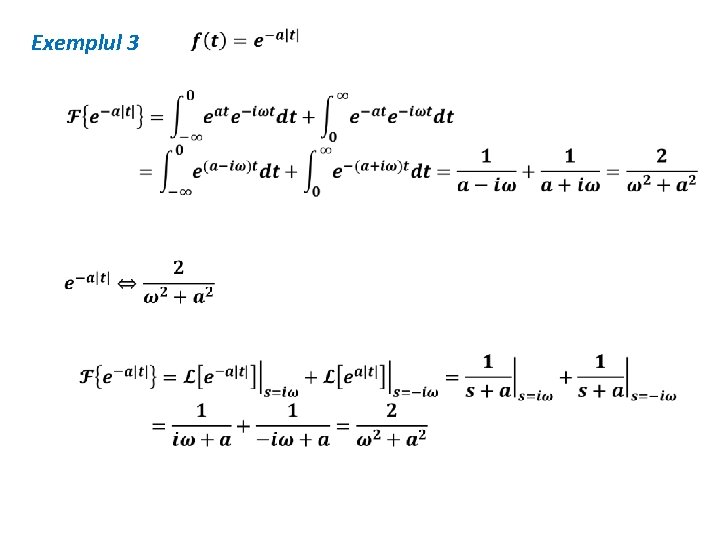
Exemplul 3

TRANSFORMATELE FOURIER ALE UNOR FUNCŢII UZUALE


UTILIZAREA MATLAB PENTRU CALCULUL TRANSFORMATELOR FOURIER DIRECTĂ ŞI INVERSĂ


APLICAŢII ÎN ANALIZA CIRCUITELOR

 Fourier series
Fourier series Trasformata di fourier gradino
Trasformata di fourier gradino Transformata laplace
Transformata laplace Transformata fourier
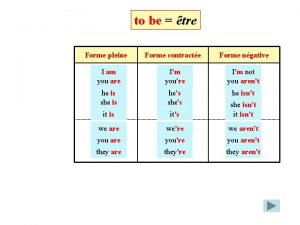
Transformata fourier Phrases affirmatives
Phrases affirmatives Povrsina figure ogranicene krivama
Povrsina figure ogranicene krivama Integrali formule
Integrali formule Uvedba nove spremenljivke integral
Uvedba nove spremenljivke integral Racunanje integrala
Racunanje integrala Transformata z
Transformata z Szybka transformata fouriera
Szybka transformata fouriera Fourier transform definition
Fourier transform definition Sinogramma
Sinogramma Transformata fouriera przykłady
Transformata fouriera przykłady Wzim plan
Wzim plan Rumus khusus fungsi invers
Rumus khusus fungsi invers Monoton murni
Monoton murni Matriks pangkat
Matriks pangkat Laplace transform formulas
Laplace transform formulas Hitunglah masing-masing koefisien masukannya
Hitunglah masing-masing koefisien masukannya Adjective matriks
Adjective matriks Invers matriks 2x2
Invers matriks 2x2 Slidetodoc.com
Slidetodoc.com Invers matrisk
Invers matrisk Misal f(x)=3x2-1 dan g(x)=2x-1/x+2
Misal f(x)=3x2-1 dan g(x)=2x-1/x+2 Invers konvers dan kontraposisi
Invers konvers dan kontraposisi Invers feedback
Invers feedback Z transform z/z-a
Z transform z/z-a Rapoarte derivate
Rapoarte derivate Invers. cap. tª.
Invers. cap. tª. Majemuk artinya
Majemuk artinya Matriks determinan
Matriks determinan Transfose
Transfose