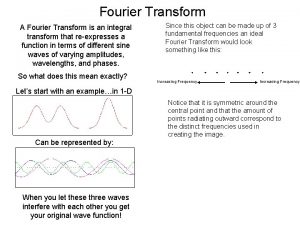
The Fourier Transform Some Fourier Transform theorems t

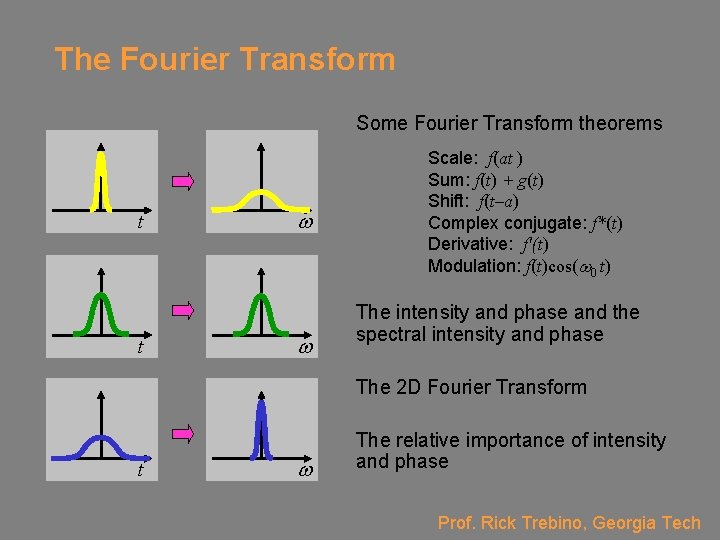
The Fourier Transform Some Fourier Transform theorems t t w w Scale: f(at ) Sum: f(t) + g(t) Shift: f(t–a) Complex conjugate: f*(t) Derivative: f'(t) Modulation: f(t)cos(w 0 t) The intensity and phase and the spectral intensity and phase The 2 D Fourier Transform t w The relative importance of intensity and phase Prof. Rick Trebino, Georgia Tech

The Fourier Transform and its Inverse

Scale Theorem The Fourier transform of a scaled function, f(at): Proof: Assuming a > 0, change variables: u = at, so dt = du / a If a < 0, the limits flip when we change variables, introducing a minus sign, hence the absolute value.

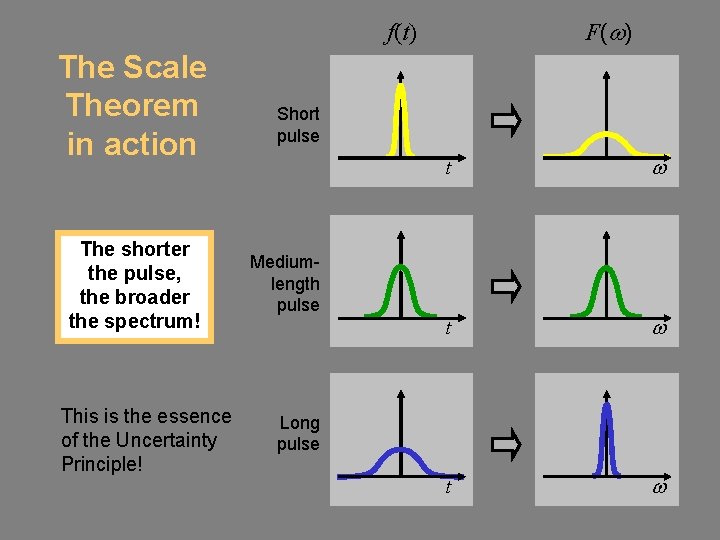
F(w) f(t) The Scale Theorem in action The shorter the pulse, the broader the spectrum! This is the essence of the Uncertainty Principle! Short pulse t w t w Mediumlength pulse Long pulse

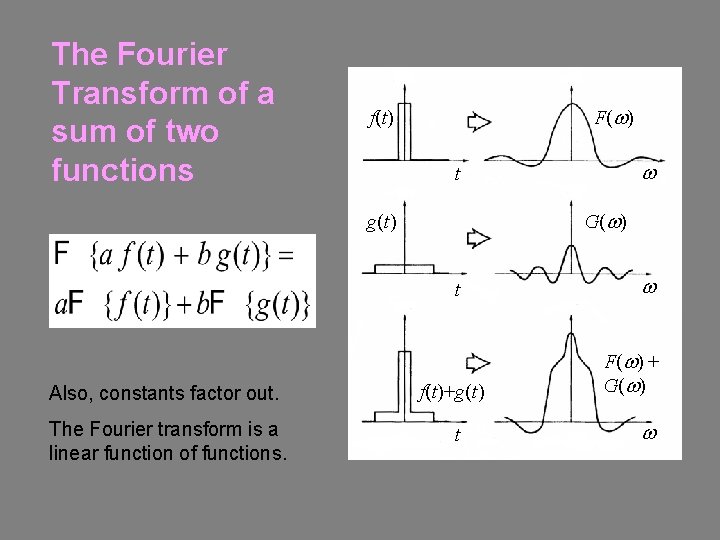
The Fourier Transform of a sum of two functions F(w) f(t) w t G(w) g(t) t Also, constants factor out. f(t)+g(t) The Fourier transform is a linear function of functions. t w F(w) + G(w) w

Shift Theorem

Application of the Shift Theorem Suppose we’re measuring the spectrum of E(t), but a small fraction of its irradiance, say e, takes a longer path to the spectrometer. The extra light has the field, √e E(t–a), where a is the extra path. The measured spectrum is: Performing the Fourier Transform and using the Shift Theorem: e E(t-a) E(t) Spectrometer

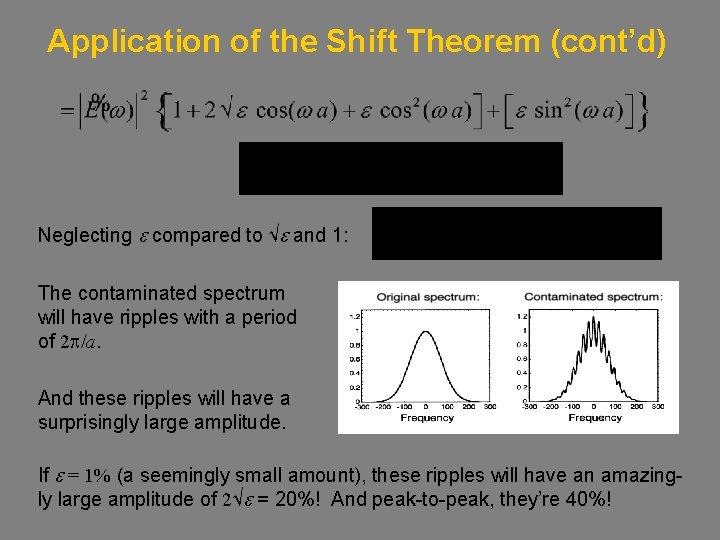
Application of the Shift Theorem (cont’d) Neglecting e compared to √e and 1: The contaminated spectrum will have ripples with a period of 2 p/a. And these ripples will have a surprisingly large amplitude. If e = 1% (a seemingly small amount), these ripples will have an amazingly large amplitude of 2√e = 20%! And peak-to-peak, they’re 40%!

The Fourier Transform of the complex conjugate of a function Proof:

Negative frequencies contain no additional information for real functions. If a function is real (e. g. , a light wave!), then f*(t) = f(t). So: Using the result we just proved: So, at –w, the real part of the Fourier transform of f is the same as at +w. And the imaginary part is just the negative of it.

Derivative Theorem The Fourier transform of a derivative of a function, f’(t): Proof: Integrate by parts: Remember that the function must be zero at ±∞, so the other term, [f(t) exp(-iwt)] +-∞ ∞ vanishes.

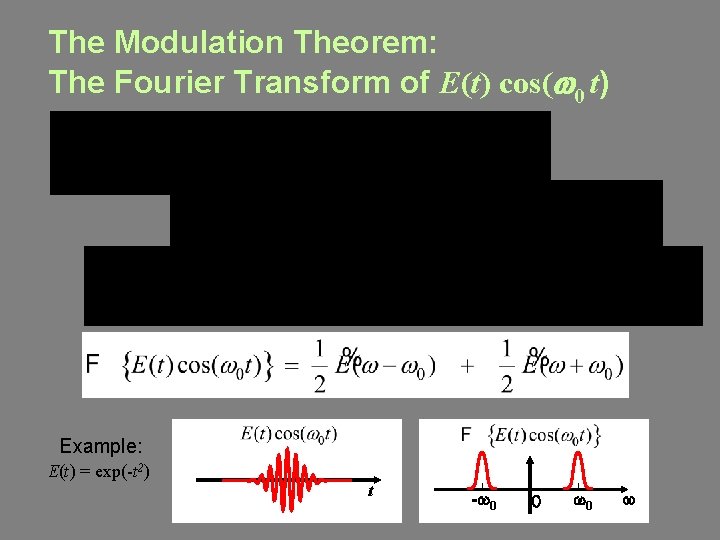
The Modulation Theorem: The Fourier Transform of E(t) cos(w 0 t) Example: E(t) = exp(-t 2) t -w 0 0 w

The Fourier transform and its inverse are symmetrical: f(t) F(w) and F(t) f(w) (almost). If f(t) Fourier transforms to F(w), then F(t) Fourier transforms to: Rearranging: Relabeling the integration variable from t to w’, we can see that we have an inverse Fourier transform: This is why it is often said that f and F are a Fourier Transform Pair.

Fourier Transform Magnitude and Phase As with any complex quantity, we can decompose f(t) and F(w) into their magnitude and phase. f(t) can be written: f(t) = Mag{f(t)} exp[ -i Phase{f(t)}] where Mag{f(t)}2 is often called the intensity, I(t), and Phase{f(t)} is called the phase, f(t). They’re the same quantities we’re used to for light waves (the minus signs are arbitrary). Analogously, F(w) = Mag{F(w)} exp[ -i Phase{F(w)}] The Mag{F(w)}2 is called the spectrum, S(w), and the Phase{F(w)} is called the spectral phase, j(w). Just as both the intensity and phase are required to specify f(t), both the spectrum and spectral phase are required to specify F(w), and hence f(t).

Light has intensity and phase also. We usually extract out the carrier frequency. A light wave has the time-domain electric field: Intensity Equivalently, vs. frequency: Spectrum The minus signs are just conventions. Phase (neglecting the negative-frequency component) Spectral Phase Knowledge of the intensity and phase or the spectrum and spectral phase is sufficient to determine the light wave.

Calculating the Intensity and the Phase It’s easy to go back and forth between the electric field and the intensity and phase. The intensity: I(t) = |E(t)|2 The phase: E(ti) √I i (t ) Im -f(ti) Equivalently, f(t) = -Im{ ln[E(t) ] } We can do the same for the field in the frequency domain. Re

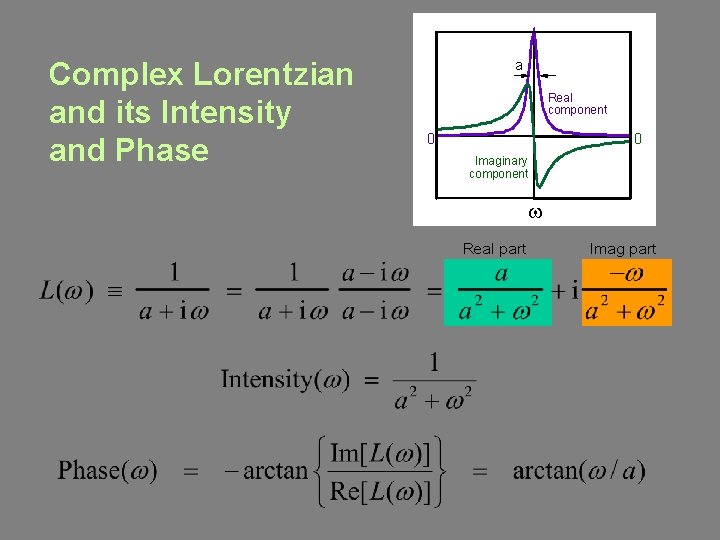
Complex Lorentzian and its Intensity and Phase a Real component 0 0 Imaginary component w Real part Imag part

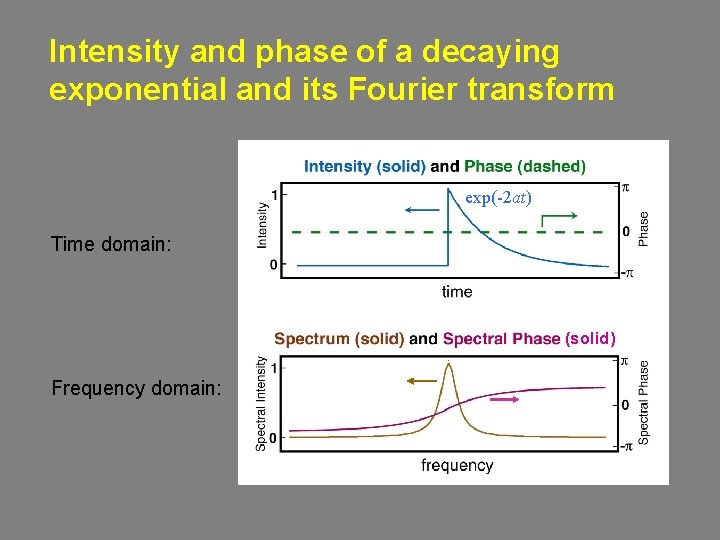
Intensity and phase of a decaying exponential and its Fourier transform exp(-2 at) Time domain: (solid) Frequency domain:

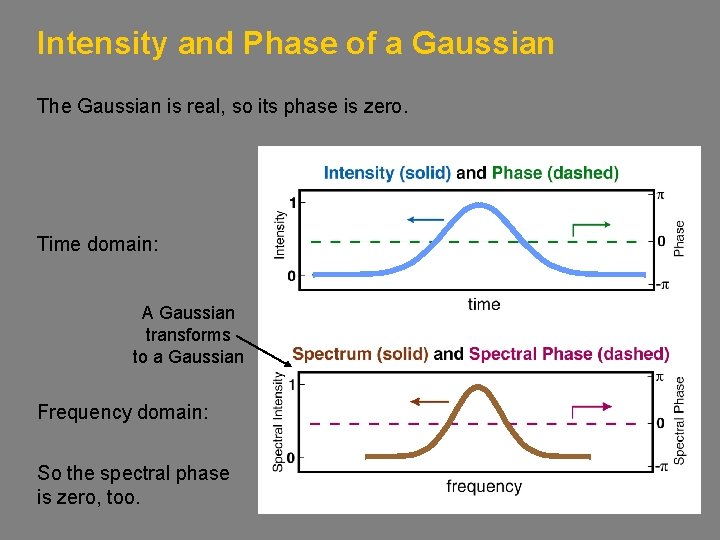
Intensity and Phase of a Gaussian The Gaussian is real, so its phase is zero. Time domain: A Gaussian transforms to a Gaussian Frequency domain: So the spectral phase is zero, too.

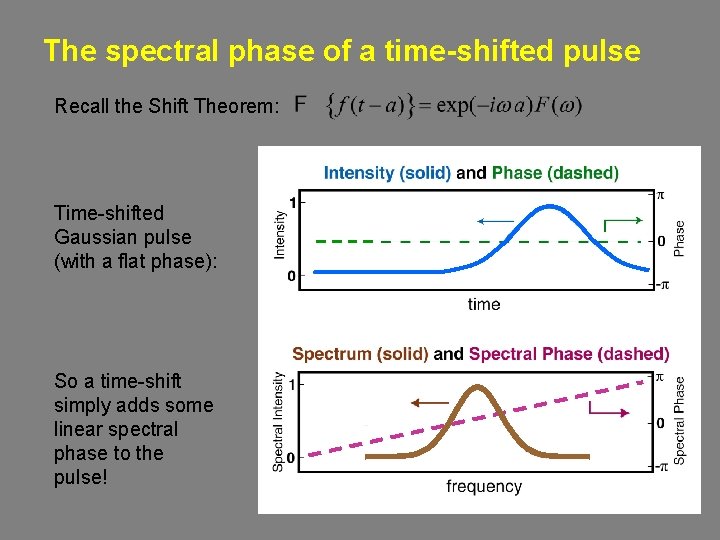
The spectral phase of a time-shifted pulse Recall the Shift Theorem: Time-shifted Gaussian pulse (with a flat phase): So a time-shift simply adds some linear spectral phase to the pulse!

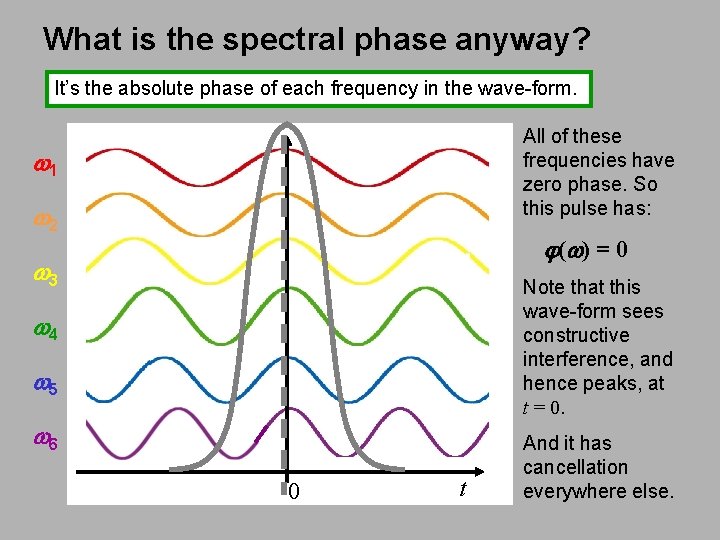
What is the spectral phase anyway? It’s the absolute phase of each frequency in the wave-form. All of these frequencies have zero phase. So this pulse has: w 1 w 2 j (w ) = 0 w 3 Note that this wave-form sees constructive interference, and hence peaks, at t = 0. w 4 w 5 w 6 0 t And it has cancellation everywhere else.

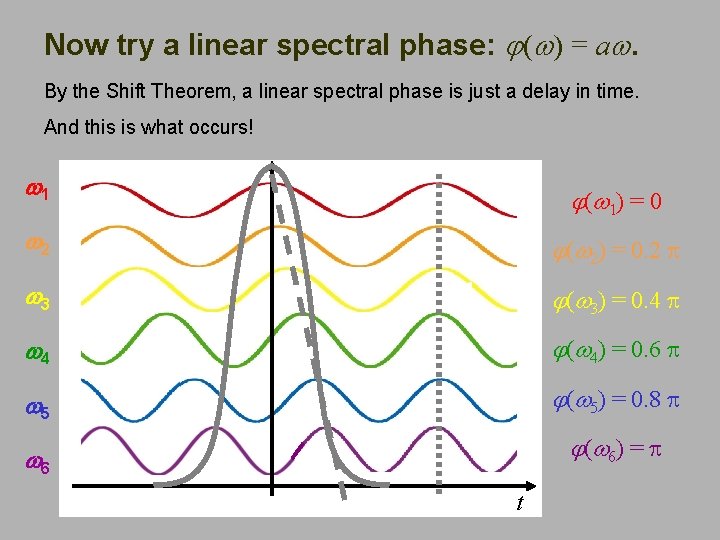
Now try a linear spectral phase: j(w) = aw. By the Shift Theorem, a linear spectral phase is just a delay in time. And this is what occurs! w 1 j(w 1) = 0 w 2 j(w 2) = 0. 2 p w 3 j(w 3) = 0. 4 p w 4 j(w 4) = 0. 6 p w 5 j(w 5) = 0. 8 p w 6 j(w 6) = p t

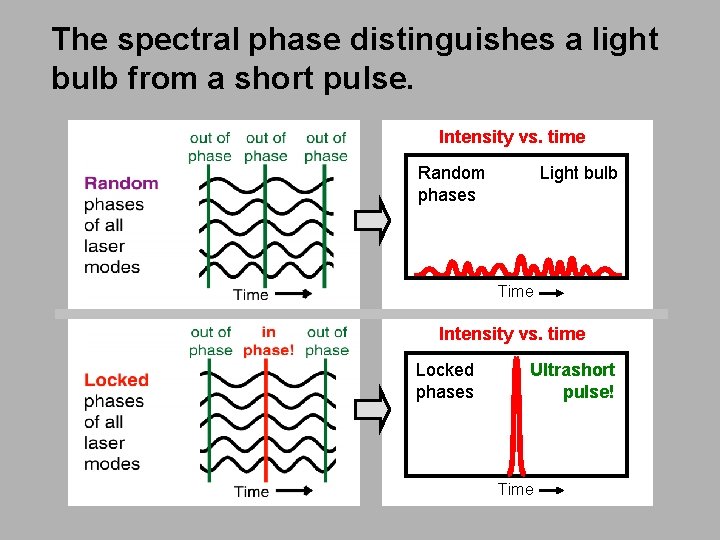
The spectral phase distinguishes a light bulb from a short pulse. Intensity vs. time Random phases Light bulb Time Intensity vs. time Locked phases Ultrashort pulse! Time

Fourier Transform with respect to space If f(x) is a function of position, x F {f(x)} = F(k) We refer to k as the spatial frequency. k Everything we’ve said about Fourier transforms between the t and w domains also applies to the x and k domains.

The 2 D Fourier Transform F = If (2){f(x, y)} f(x, y) = F(kx, ky) f(x, y) exp[-i(kxx+kyy)] dx dy f(x, y) = fx(x) fy(y), then the 2 D FT splits into two 1 D FT's. But this doesn’t always happen. x F y (2){f(x, y)}

A 2 D Fourier Transform: a square function f(x, y) Consider a square function in the xy plane: f(x, y) = rect(x) rect(y) The 2 D Fourier Transform splits into the product of two 1 D Fourier Transforms: F {f(x, y)} = sinc(kx/2) sinc(ky/2) This picture is an optical determination of the Fourier Transform of the square function! x F y (2){f(x, y)}

Fourier Transform Magnitude and Phase Rick Linda Pictures reconstructed using the spectral phase of the other picture Mag{F [Linda]} Phase{F [Rick]} Mag{F [Rick]} Phase{F {Linda]} The phase of the Fourier transform (spectral phase) is much more important than the magnitude in reconstructing an image.