Circularly Symmetric Functions Hankel Transforms of Zeroth Order










- Slides: 11

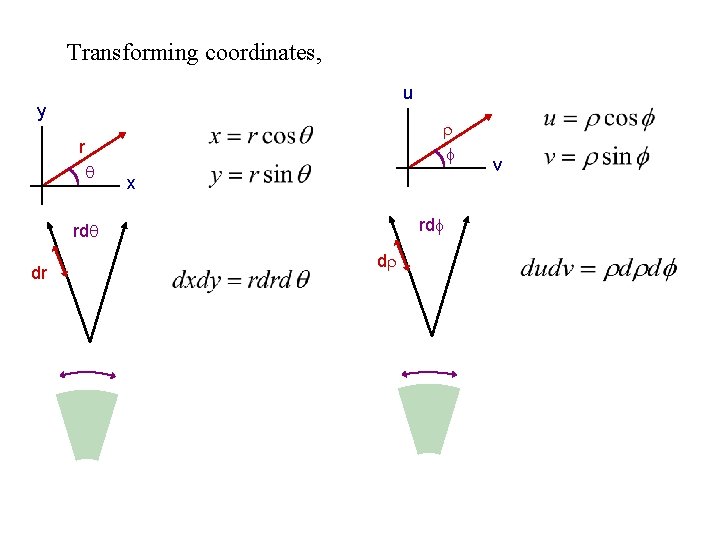
Circularly Symmetric Functions: Hankel Transforms of Zeroth Order, or, Fourier-Bessel Transforms What if our function is expressed in polar coordinates? …and is separable in those coordinates? Why is this of interest? Useful for modeling circular sources, lesions, lenses, etc. Circular symmetry: (no dependence on angle)

Transforming coordinates, u y r x rd dr d v

Hankel Transform, continued transforming variables. . . where (Using Trig Identity) So, But, this can be simplified by using

Bessel functions Jn(x) is a Bessel function of the first kind of order n. Useful identities, and where J 1(x) is a Bessel function of the first kind of order 1.

Hankel Transform, continued (2) (from previous slide) But, Subbing in Jo(2 r ) yields which is not a function of . Thus, the function is circularly symmetric in both domains.

The Inverse Hankel Transform Circularly symmetric in space Circularly symmetric in spatial frequency Notice no difference in sign between forward and inverse transforms

Example: Hankel transform of a circle Consider the Fourier Transform of a circle: assume (circular symmetry) y r=1 Consider g r(r) = circ(r) x Let Then, and

Hankel Transform of Circle, continued Subbing in r’=2 r yields Note: So

Jinc Function We define the jinc function as Similar to sinc function, only sinc has zeros are at equal intervals, jinc zeros vary

Hankel Transform of Circ circ(r) F. T { fft(circ(r))} = jinc(r) Log 10(abs(fft(circ(r)))

Hankel Transform Scaling Property The only difference between the Fourier and Hankel transform scaling property is the scalar 1/a 2 The scalar takes into account that the function is expanding or contracting in 2 dimensions.
 Hankel functions
Hankel functions Zero order elimination drugs
Zero order elimination drugs Symmetric and skew symmetric matrix
Symmetric and skew symmetric matrix Asu
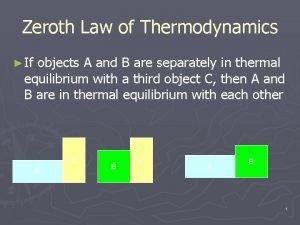
Asu Zeroth law of thermodynamics definition
Zeroth law of thermodynamics definition Zeroth law of thermodynamics statement
Zeroth law of thermodynamics statement Zeroth law of thermodynamics
Zeroth law of thermodynamics Zeroth law of thermodynamics
Zeroth law of thermodynamics Zeroth law of thermodynamics
Zeroth law of thermodynamics 1st order 2nd order 3rd order neurons
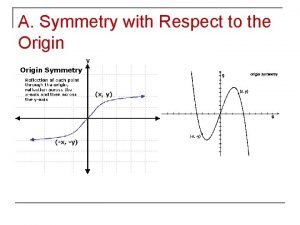
1st order 2nd order 3rd order neurons Symmetric with respect to
Symmetric with respect to Eurylochus odyssey
Eurylochus odyssey