Fourier Transform chapter 6 FOURIER TRANSFORM Definition of

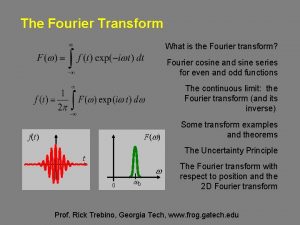
Fourier Transform chapter 6

FOURIER TRANSFORM: • Definition of the Fourier transforms • Relationship between Laplace Transforms and Fourier Transforms • Fourier transforms in the limit • Properties of the Fourier Transforms • Circuit applications using Fourier Transforms • Parseval’s theorem • Energy calculation in magnitude spectrum

Definition of Fourier Transforms:

Inverse Fourier Transforms:

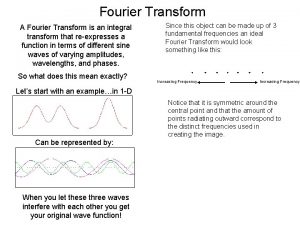
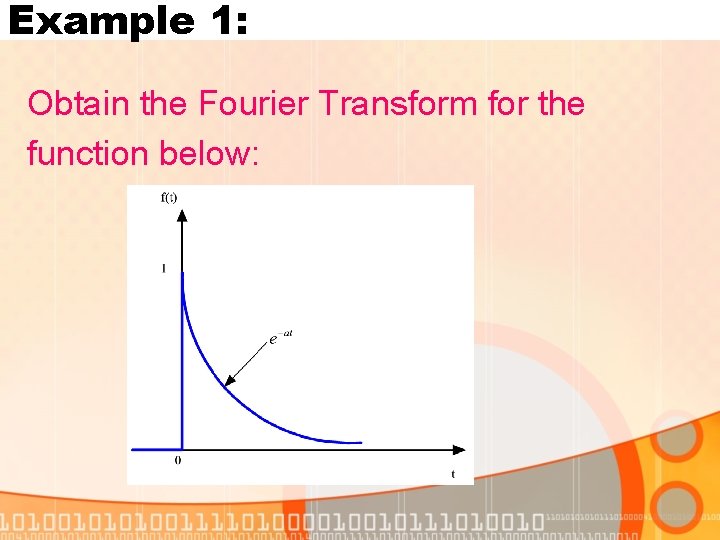
Example 1: Obtain the Fourier Transform for the function below:

Solution: Given function is:

Fourier Transforms:

FOURIER TRANSFORM: • Definition of the Fourier transforms • Relationship between Laplace Transforms and Fourier Transforms • Fourier transforms in the limit • Properties of the Fourier Transforms • Circuit applications using Fourier Transforms • Parseval’s theorem • Energy calculation in magnitude spectrum

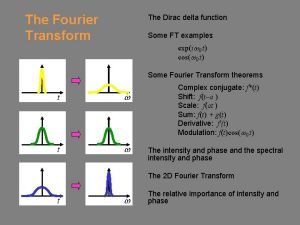
Relationship between Fourier Transforms and Laplace Transforms There are 3 rules apply to the use of Laplace transforms to find Fourier Transforms of such functions.

Rule 1: If f(t)=0 for t<=0 • Replace s=jω

Example:

Replace s=jω

Rule 2: Inverse negative function

Example: Negative

Fourier Transforms

Rule 3: Add the positive and negative function

Thus,

Example 1:

Fourier transforms:

Example 2: Obtain the Fourier Transforms for the function below:

Solution:

Example 3:

Solution:

Example 4:

Solution:

FOURIER TRANSFORM: • Definition of the Fourier transforms • Relationship between Laplace Transforms and Fourier Transforms • Fourier transforms in the limit • Properties of the Fourier Transforms • Circuit applications using Fourier Transforms • Parseval’s theorem • Energy calculation in magnitude spectrum

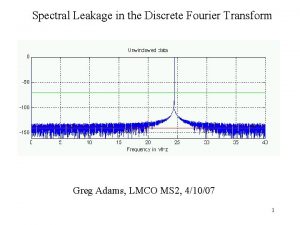
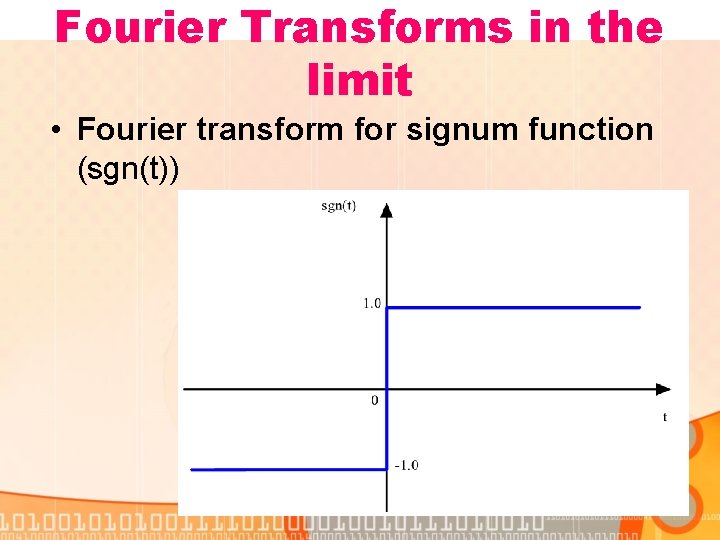
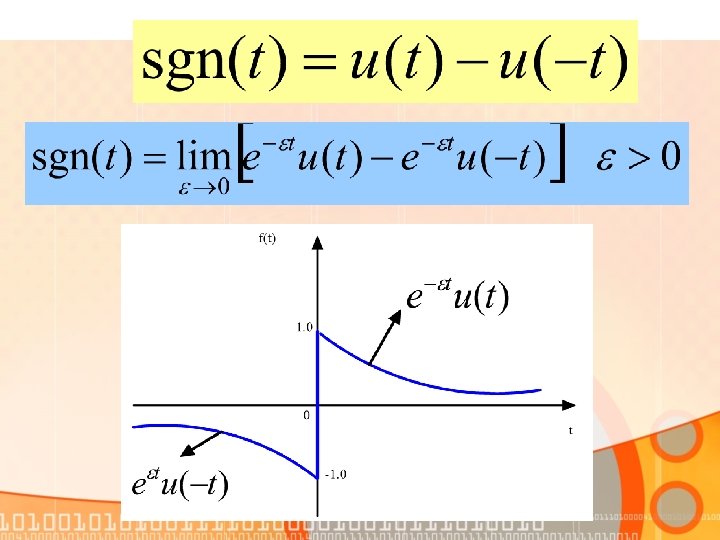
Fourier Transforms in the limit • Fourier transform for signum function (sgn(t))

assume ε→ 0,

• Fourier Transforms for step function:

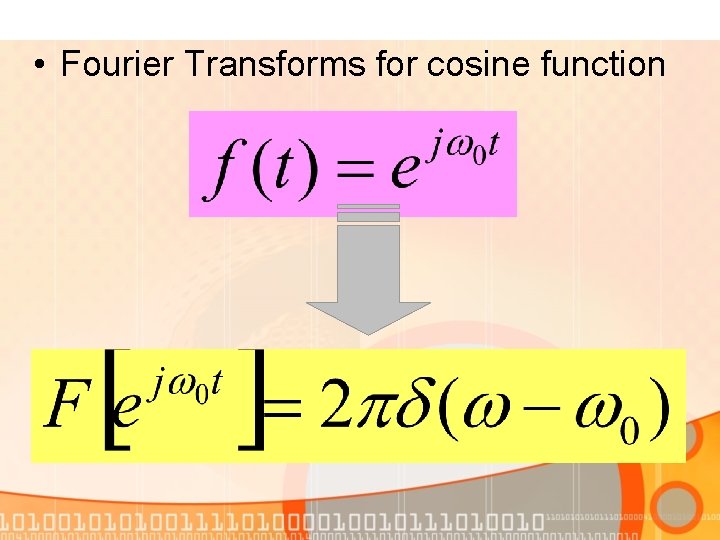
• Fourier Transforms for cosine function

Thus,

FOURIER TRANSFORM: • Definition of the Fourier transforms • Relationship between Laplace Transforms and Fourier Transforms • Fourier transforms in the limit • Properties of the Fourier Transforms • Circuit applications using Fourier Transforms • Parseval’s theorem • Energy calculation in magnitude spectrum

Properties of Fourier Transforms • Multiplication by a constant

• Addition and subtraction

• Differentiation

• Integration

• Scaling

• Time shift

• Frequency shift

• Modulation

• Convolution in time domain

• Convolution in frequency domain:

Example 1: • Determine the inverse Fourier Transforms for the function below:

Solution: LAPLACE TRANSFORMS

• A and B value: