Fast Fourier Transform FFT Corso di Metodi per

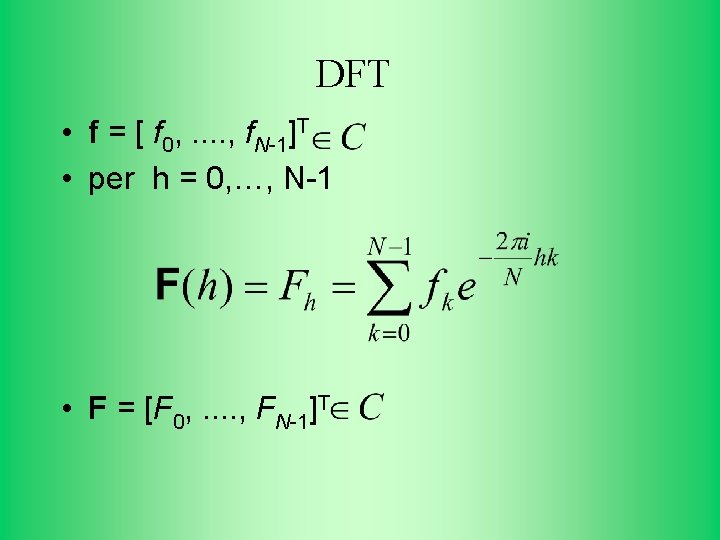





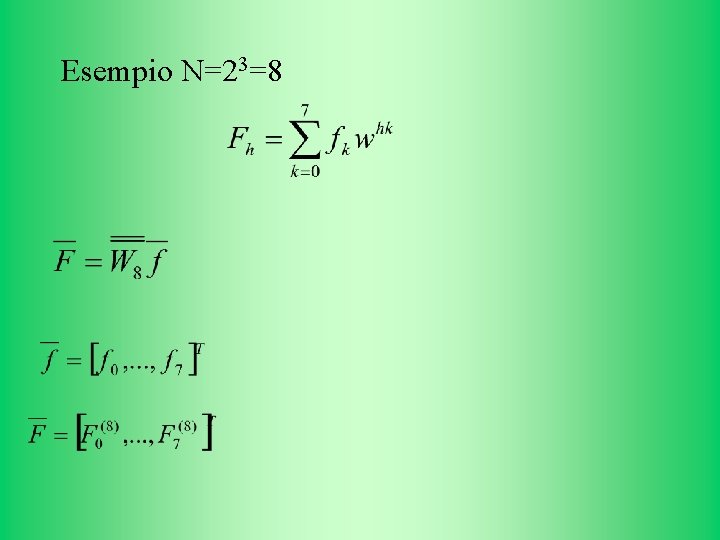

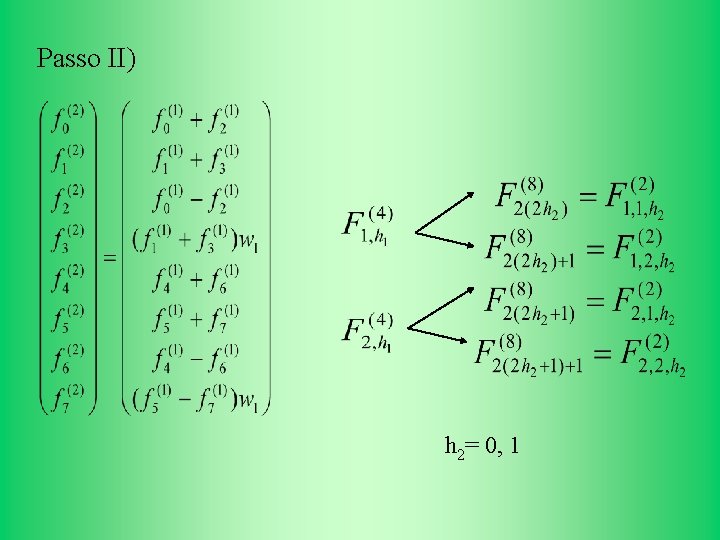




![Bibliografia [1] – Cooley J. W. e Tukey J. W. , An algorithm for Bibliografia [1] – Cooley J. W. e Tukey J. W. , An algorithm for](https://slidetodoc.com/presentation_image/10f9d62f27c8ca8e6b20520b9cd74988/image-20.jpg)
- Slides: 20

Fast Fourier Transform (FFT) Corso di Metodi per il Trattamento Numerico di Dati Multimediali Laura Patricolo (50/174) Valeria Mele (50/18)
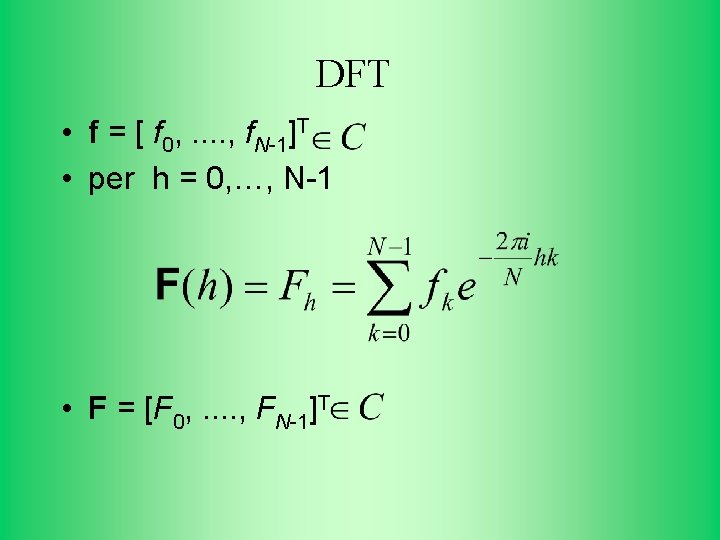

DFT Forma matriciale: Con

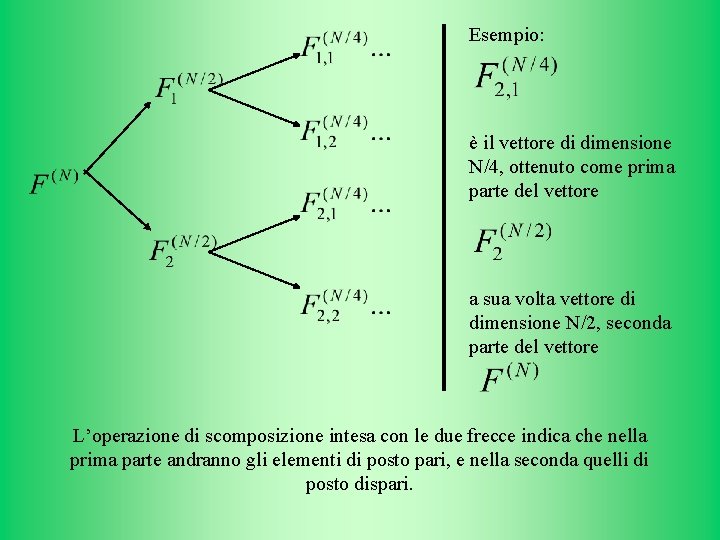
Esempio: è il vettore di dimensione N/4, ottenuto come prima parte del vettore a sua volta vettore di dimensione N/2, seconda parte del vettore L’operazione di scomposizione intesa con le due frecce indica che nella prima parte andranno gli elementi di posto pari, e nella seconda quelli di posto dispari.

Scomposizione formale per h = 0, …, N-1

Osserviamo:

Componenti pari: f (1)k Componenti dispari: f(1) k+(n/2) h 1 = 0, …, (N/2)-1 N. B. : l’apice accanto a f indica il passo di scomposizione corrente !!

due trasformate di ordine N/2 Trasformando Vettore delle componenti di posto pari di F Trasformando Vettore delle componenti di posto dispari di F
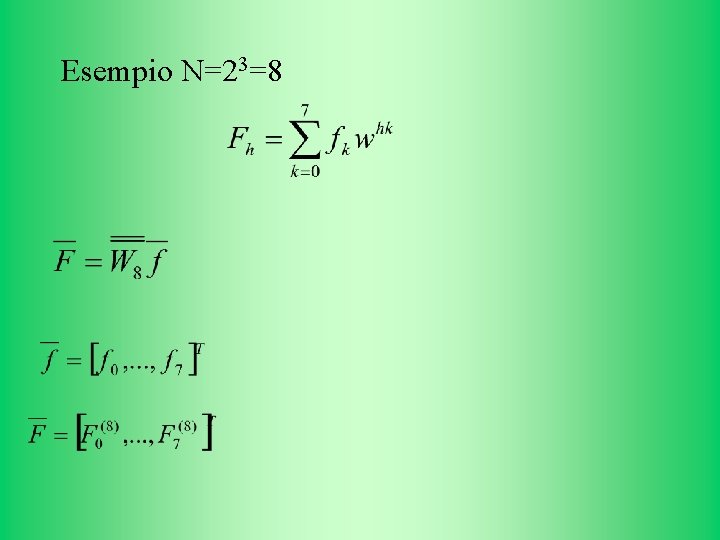
Esempio N=23=8

Passo I) RICORDA: nella notazione di F l’apice esprime la dimensione del problema, il pedice porta traccia della scomposizione del vettore, indicando la relazione del vettore al passo corrente con quello al passo precedente. Nella notazione di f invece l’apice esprime il passo corrente. NOTA: In questo momento il pedice di F contiene anche l’indice dell’elemento generico (h 1). h 1= 0, 1, 2, 3
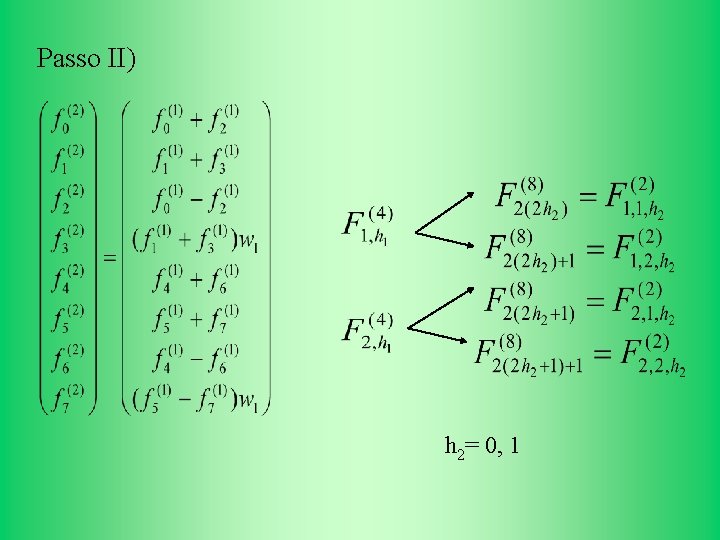
Passo II) h 2= 0, 1

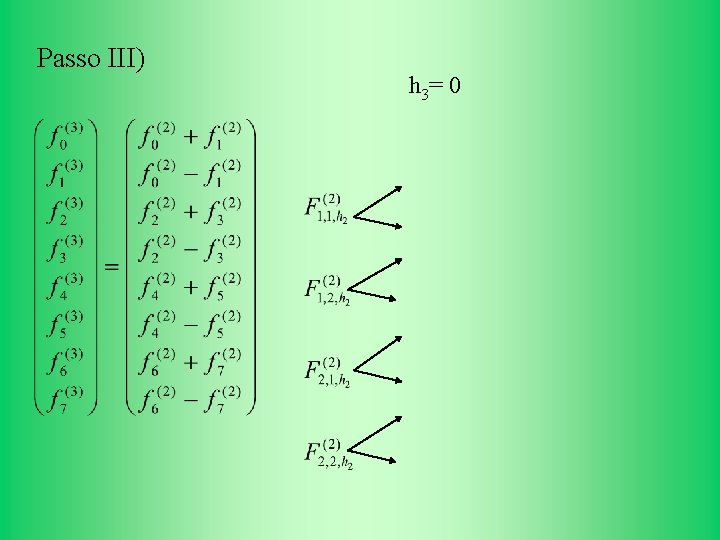
Passo III) h 3= 0

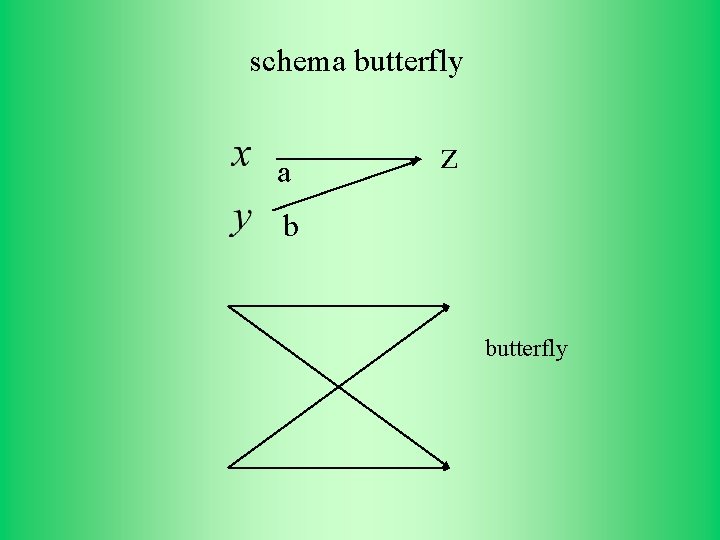
schema butterfly a z b butterfly

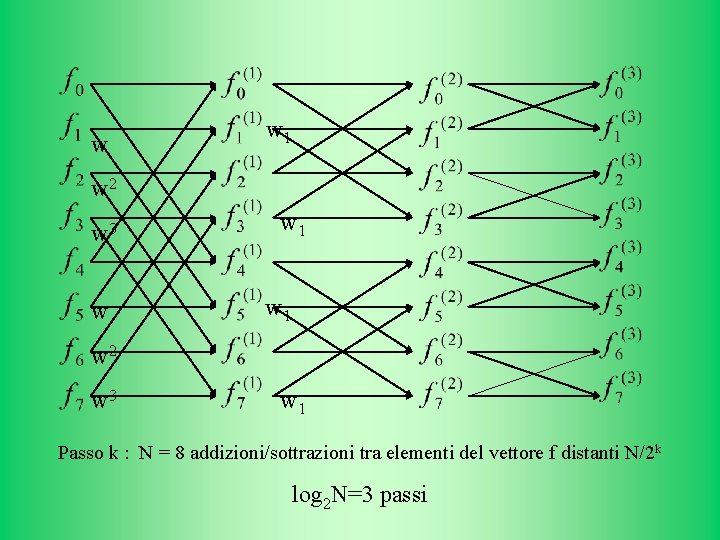
w w 1 w 2 w 3 w 1 Passo k : N = 8 addizioni/sottrazioni tra elementi del vettore f distanti N/2 k log 2 N=3 passi

Abbiamo ridotto il numero delle addizioni/sottrazioni necessarie al calcolo della nostra DFT a N log 2 N = 8*3 = 24 invece che N 2=64 come richieste dall’algoritmo classico

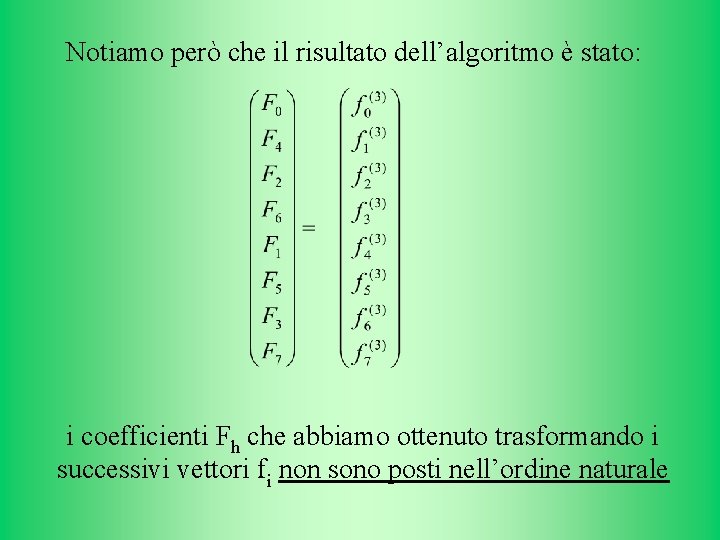
Notiamo però che il risultato dell’algoritmo è stato: i coefficienti Fh che abbiamo ottenuto trasformando i successivi vettori fi non sono posti nell’ordine naturale

Integer Bit Reversal (IBR) - considera le rappresentazioni binarie degli interi 0, 1, … , N-1; - inverte le successioni di bit delle singole rappresentazioni; - determina i corrispondenti numeri decimali. h inversione

ALGORITMO FFT for m=1, z m 2=2 m-1 nm=N/2 m for i=0, m 2 step 2 for k=0, nm-1 g= fi*nm+k+ fnm+k=( fi*nm+k - f(i+1)*nm+k)wk fi*nm+k=g endfor

CONCLUSIONI La trasformata di Fourier è una tecnica che proprio nelle applicazioni, dalla fisica dei plasmi alla sismografia, dalla Tac alla oceanografia, alla ricostruzione di immagini, ha trovato la sua legittimazione come strumento principale per la risoluzione effettiva di problemi concreti. Per dare un'idea del guadagno effettivo ricordiamo che la Nasa, nell'ambito del Progetto Ciclope per la ricerca delle intelligenze extraterrestri, ha operato la trasformazione di Fourier su un insieme di un miliardo di dati; ciò ha richiesto circa 9 ore di tempo con la Fft, contro gli oltre 36. 000 anni necessari con l'algoritmo normale. Ovvero con 1024 punti il rapporto tra i tempi è pari a circa 150.
![Bibliografia 1 Cooley J W e Tukey J W An algorithm for Bibliografia [1] – Cooley J. W. e Tukey J. W. , An algorithm for](https://slidetodoc.com/presentation_image/10f9d62f27c8ca8e6b20520b9cd74988/image-20.jpg)
Bibliografia [1] – Cooley J. W. e Tukey J. W. , An algorithm for machine calculation of complex Fourier series, Maths comput. , 19, 297 – 301 (1965). [2] - D. Bini, M. Capovani, G. Lotti, F. Romani "Complessità numerica", ed. Boringhieri (1981). [3] - G. Monegato "Fondamenti di Calcolo Numerico", ed. Levrotto&Bella (1990). [4] - “www. nr. com”, by Numerical Recipes Software, pubblicato da Cambridge University Press. [5] - “www. disi. unige. it/person/Boccacci. P”, dott. P. Boccacci, Università di Genova. [6] - “http: //digilander. libero. it/nfragale/metodi/capitolo 6. html”, Libreria di Software Matematico, Manuale per l'utente. [7] - T. Scapolla dell’Università di Pavia, La trasformata di Fourier, Una formula dell'800 usata anche dalla Nasa, Tuttoscienze, inserto del quotidiano La Stampa, (1999) (reperibile all’indirizzo http: //digilander. libero. it/arti 2000/ts 99/960904. htm) [8] – “www. wikipedia. org”, Wikipedia, the free encyclopedia.