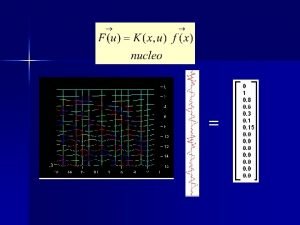
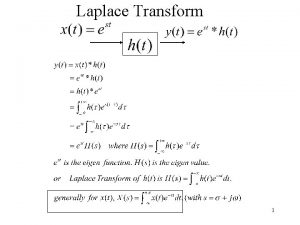ContinuousTime Fourier Transform Content l Introduction l Fourier














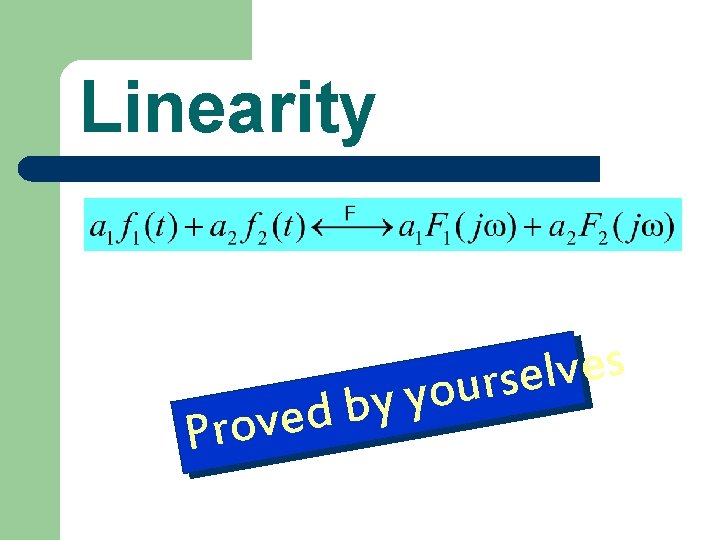















![Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution](https://slidetodoc.com/presentation_image_h/ac063b4de65a7c495b6420a7a961e189/image-45.jpg)
![Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution](https://slidetodoc.com/presentation_image_h/ac063b4de65a7c495b6420a7a961e189/image-46.jpg)














- Slides: 68

Continuous-Time Fourier Transform 主講者:虞台文

Content l Introduction l Fourier Integral l Fourier Transform l Properties of Fourier Transform l Convolution l Parseval’s Theorem

Continuous-Time Fourier Transform Introduction

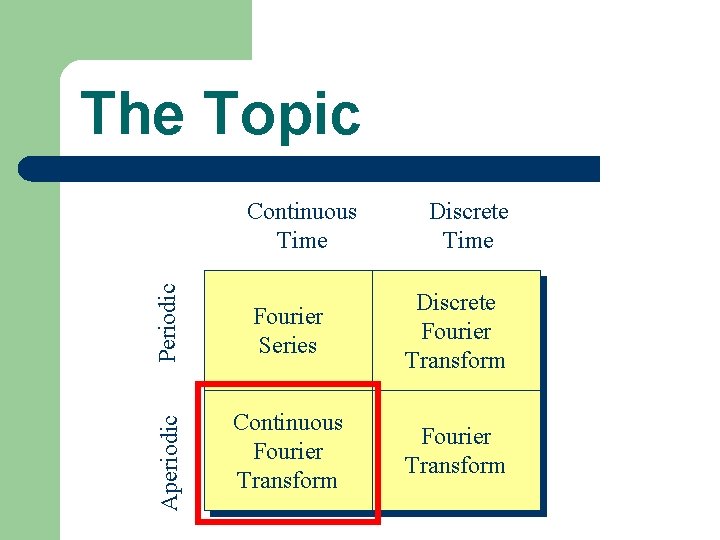
The Topic Aperiodic Periodic Continuous Time Discrete Time Fourier Series Discrete Fourier Transform Continuous Fourier Transform

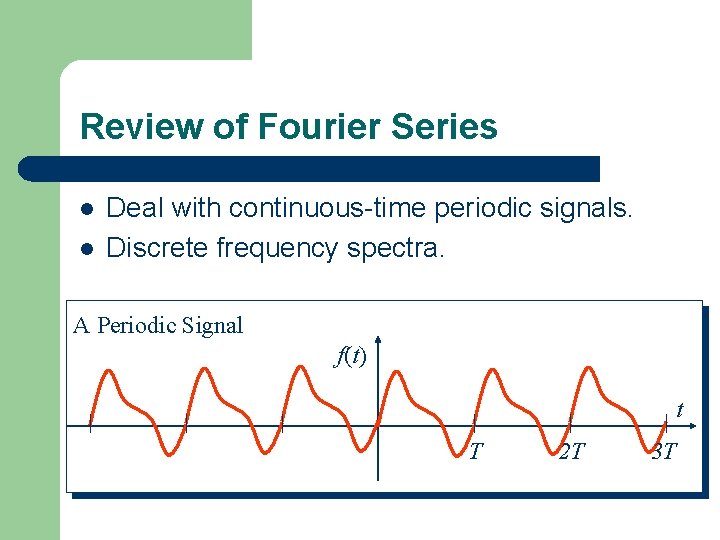
Review of Fourier Series l l Deal with continuous-time periodic signals. Discrete frequency spectra. A Periodic Signal f(t) t T 2 T 3 T

Two Forms for Fourier Series Sinusoidal Form Complex Form:

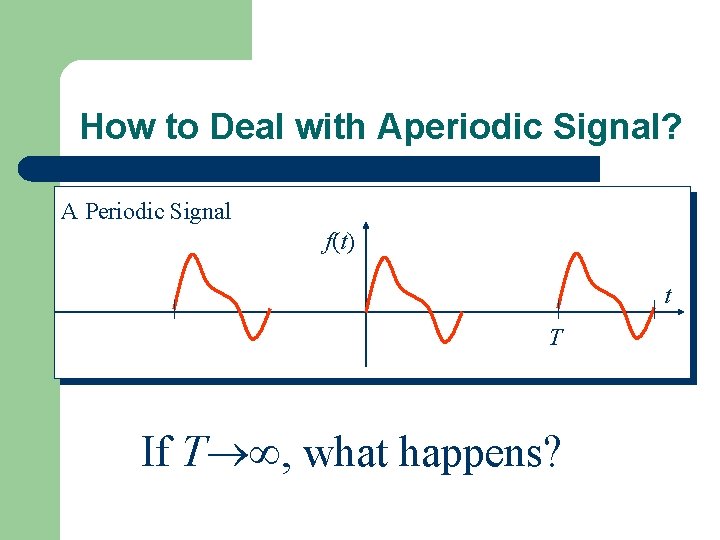
How to Deal with Aperiodic Signal? A Periodic Signal f(t) t T If T , what happens?

Continuous-Time Fourier Transform Fourier Integral

Fourier Integral Let

Fourier Integral F(j ) Synthesis Analysis

Fourier Series vs. Fourier Integral Fourier Series: Period Function Discrete Spectra Fourier Integral: Non-Period Function Continuous Spectra

Continuous-Time Fourier Transform

Fourier Transform Pair Inverse Fourier Transform: Synthesis Fourier Transform: Analysis

Existence of the Fourier Transform Sufficient Condition: f(t) is absolutely integrable, i. e. ,

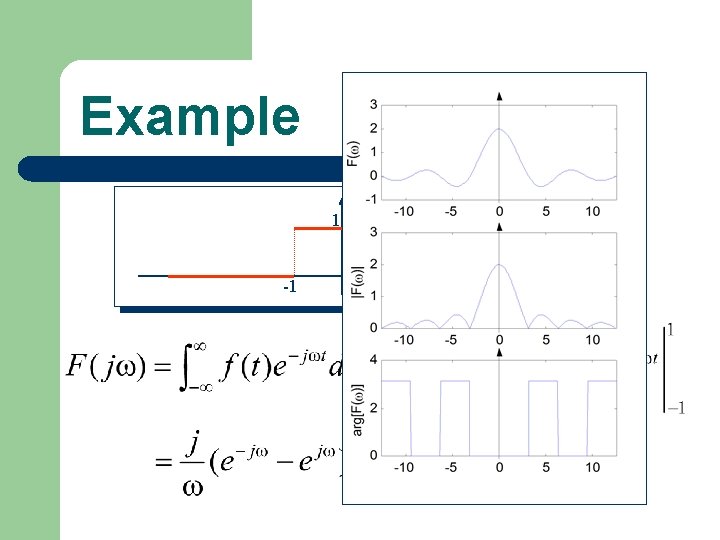
Continuous Spectra FI(j ) | ) j |F ( ( ) FR(j ) Magnitude Phase

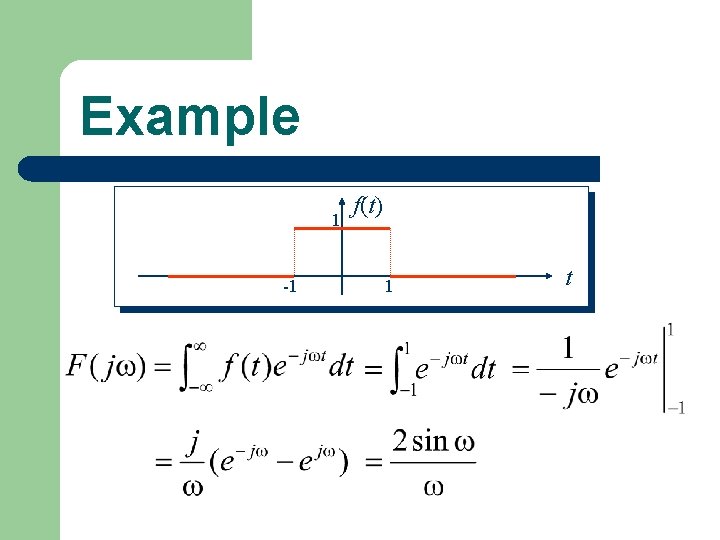
Example 1 -1 f(t) 1 t

Example 1 -1 f(t) 1 t

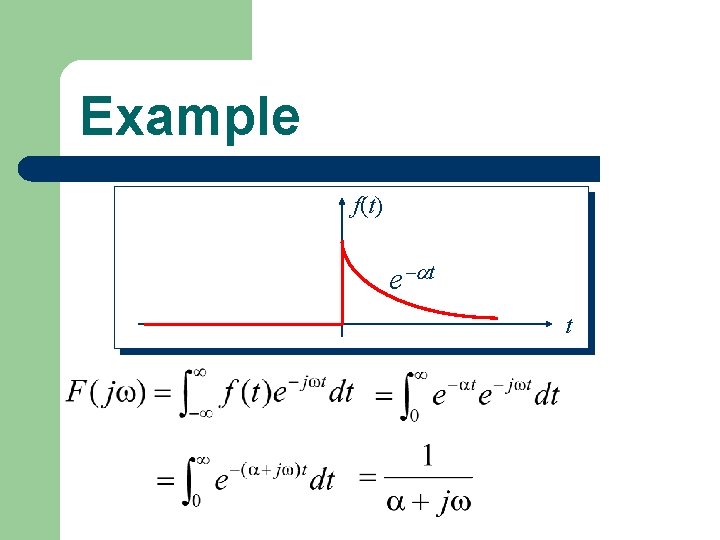
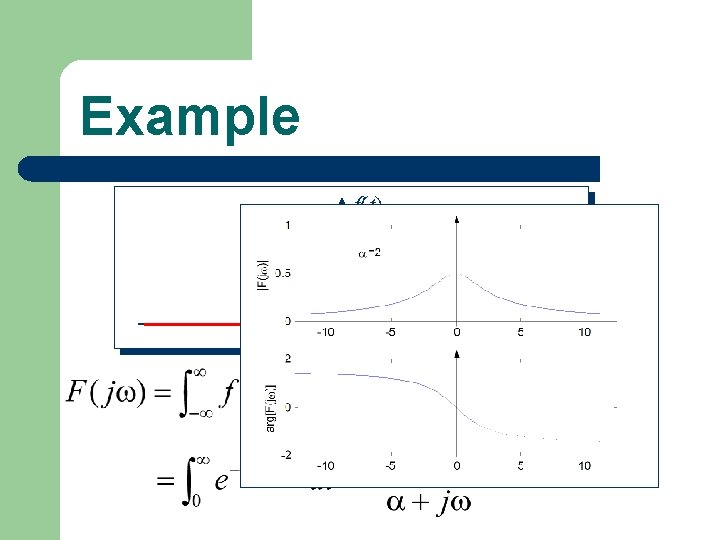
Example f(t) e t t

Example f(t) e t t

Continuous-Time Fourier Transform Properties of Fourier Transform

Notation
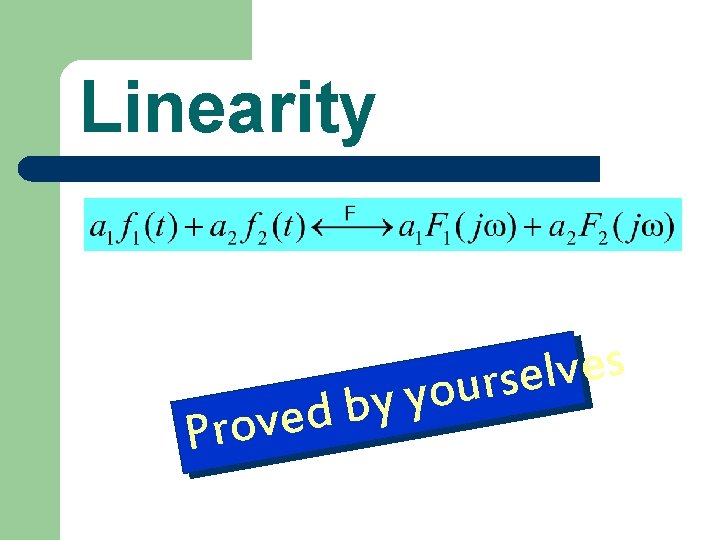
Linearity y b d e v o r P s e v l e s r u yo

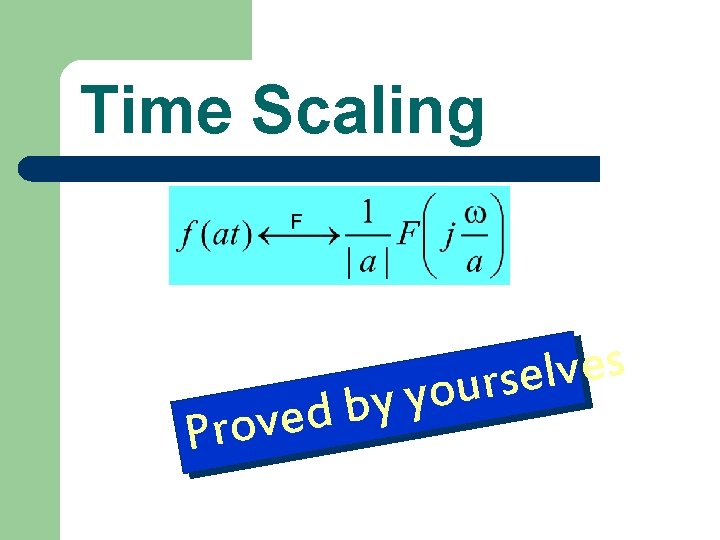
Time Scaling y b d e v o r P s e v l e s r u yo

Time Reversal Pf)

Time Shifting Pf)

Frequency Shifting (Modulation) Pf)

Symmetry Property Pf) Interchange symbols and t

Fourier Transform for Real Functions If f(t) is a real function, and F(j ) = FR(j ) + j. FI(j ) F( j ) = F*(j )

Fourier Transform for Real Functions If f(t) is a real function, and F(j ) = FR(j ) + j. FI(j ) F( j ) = F*(j ) FR(j ) is even, and FI(j ) is odd. FR( j ) = FR(j ) FI( j ) = FI(j ) Magnitude spectrum |F(j )| is even, and phase spectrum ( ) is odd.

Fourier Transform for Real Functions If f(t) is real and even F(j ) is real If f(t) is real and odd F(j ) is pure imaginary Pf) Even Pf) Odd Real

Example: Sol)

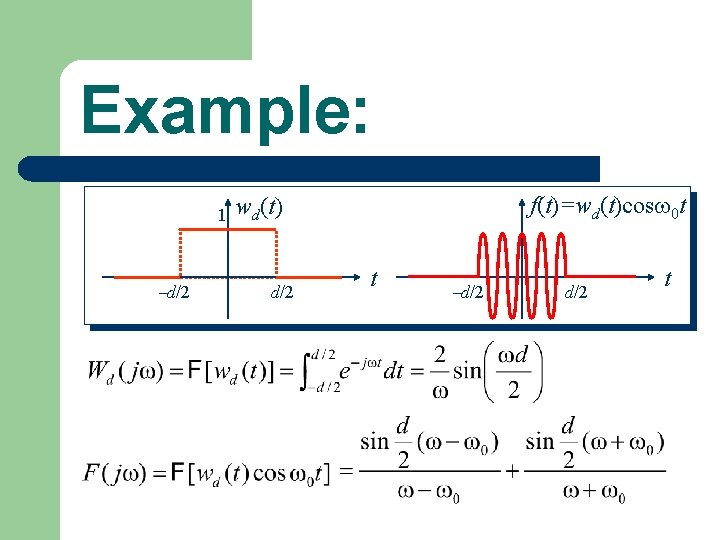
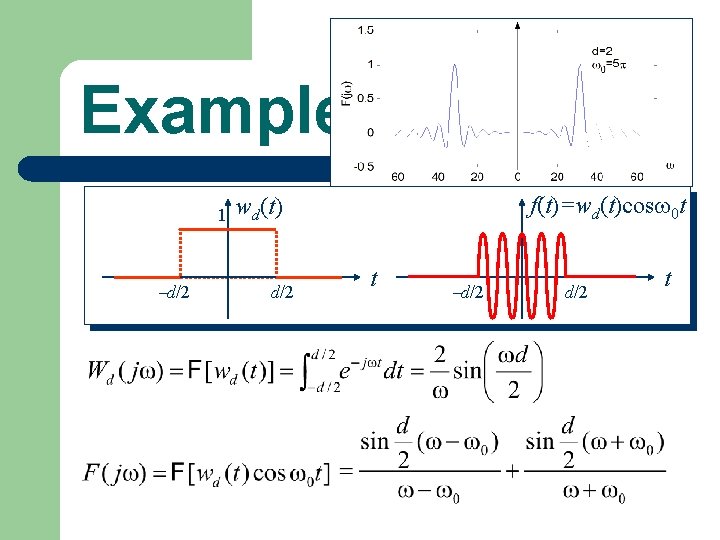
Example: 1 d/2 f(t)=wd(t)cos 0 t wd(t) d/2 t

Example: 1 d/2 f(t)=wd(t)cos 0 t wd(t) d/2 t

1 Example: Sol) wd(t) t d/2

Fourier Transform of f’(t) Pf)

Fourier Transform of f y b d e v o r P (n)(t) s e v l e s r u yo

Fourier Transform of f y b d e v o r P (n)(t) s e v l e s r u yo

Fourier Transform of Integral Let

The Derivative of Fourier Transform Pf)

Continuous-Time Fourier Transform Convolution

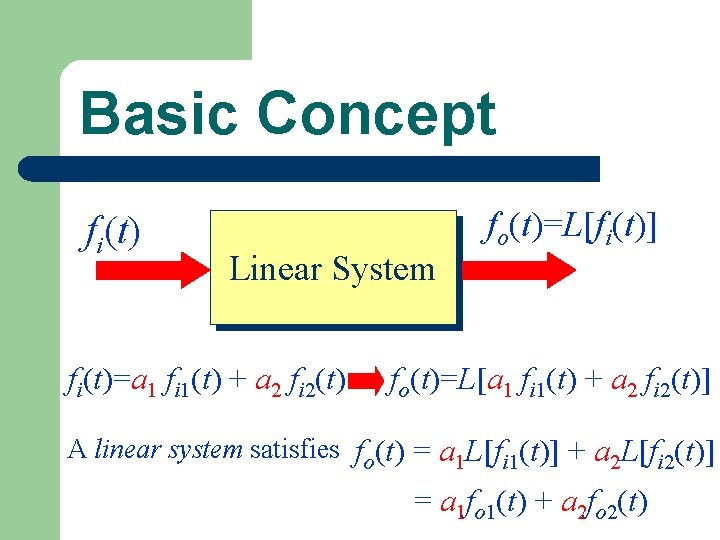
Basic Concept fi(t) Linear System fi(t)=a 1 fi 1(t) + a 2 fi 2(t) fo(t)=L[fi(t)] fo(t)=L[a 1 fi 1(t) + a 2 fi 2(t)] A linear system satisfies fo(t) = a 1 L[fi 1(t)] + a 2 L[fi 2(t)] = a 1 fo 1(t) + a 2 fo 2(t)

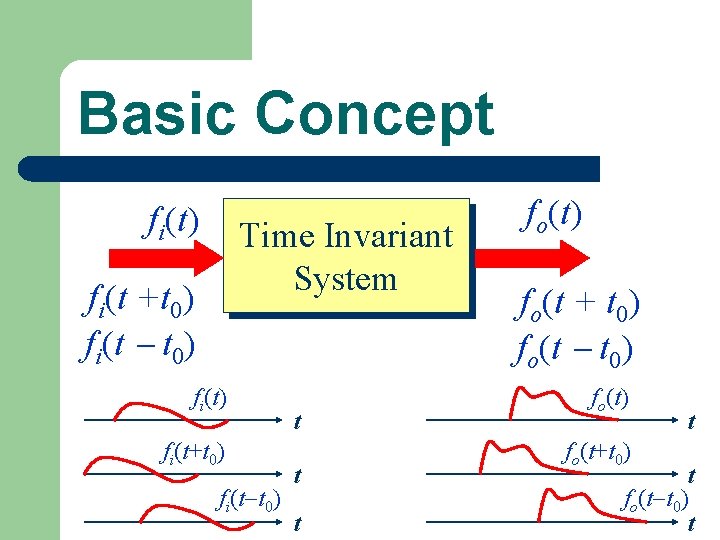
Basic Concept fi(t) Time Invariant System fi(t +t 0) fi(t t 0) fi(t+t 0) fi(t t 0) t t t fo(t) fo(t + t 0) fo(t+t 0) t t fo(t t 0) t

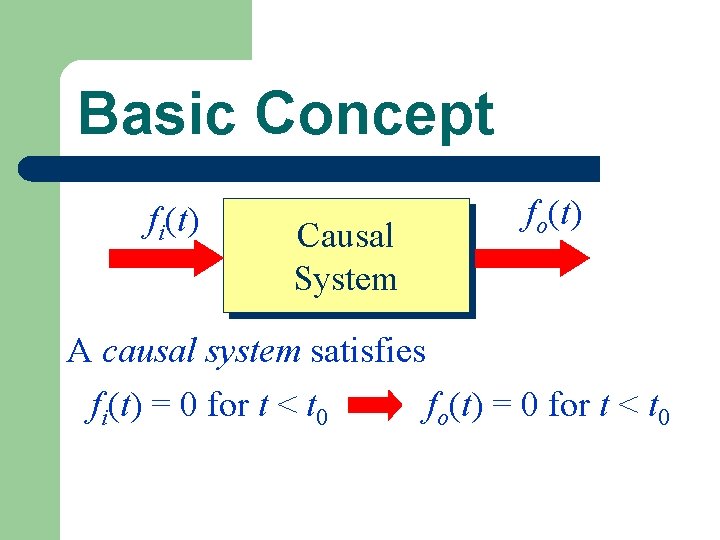
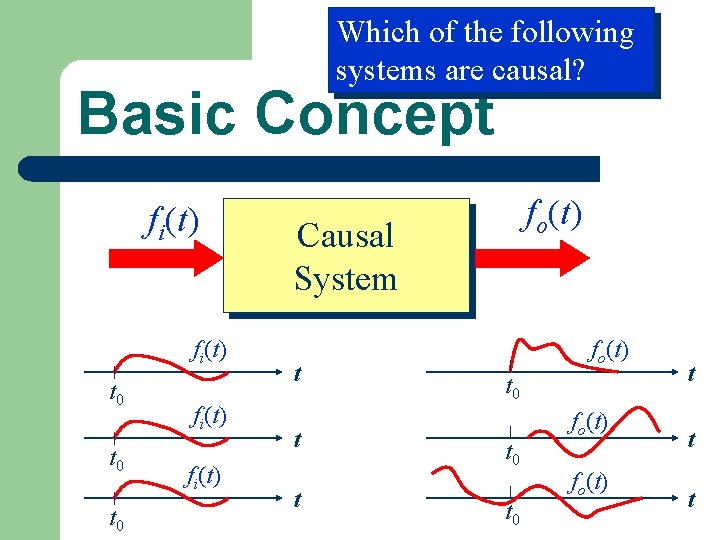
Basic Concept fi(t) Causal System fo(t) A causal system satisfies fi(t) = 0 for t < t 0 fo(t) = 0 for t < t 0

Which of the following systems are causal? Basic Concept fi(t) t 0 t 0 fi(t) fo(t) Causal System t t t fo(t) t 0 t 0 fo(t) t t t
![Unit Impulse Response t ft LTI System htL t Lft Facts Convolution Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution](https://slidetodoc.com/presentation_image_h/ac063b4de65a7c495b6420a7a961e189/image-45.jpg)
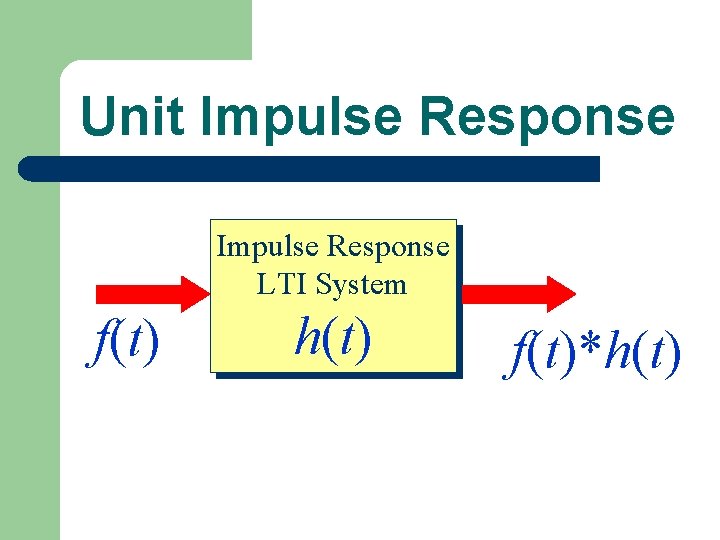
Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution
![Unit Impulse Response t ft LTI System htL t Lft Facts Convolution Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution](https://slidetodoc.com/presentation_image_h/ac063b4de65a7c495b6420a7a961e189/image-46.jpg)
Unit Impulse Response (t) f(t) LTI System h(t)=L[ (t)] L[f(t)]=? Facts: Convolution

Unit Impulse Response LTI System f(t) h(t) f(t)*h(t)

Convolution Definition The convolution of two functions f 1(t) and f 2(t) is defined as:

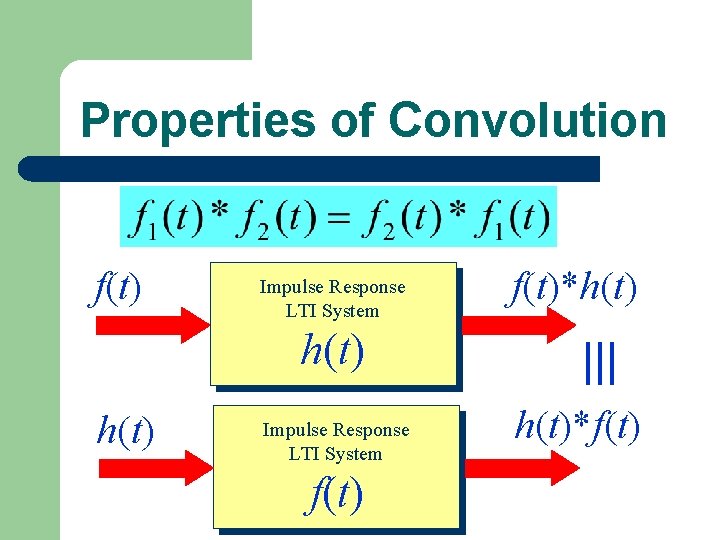
Properties of Convolution

Properties of Convolution f(t) Impulse Response LTI System f(t)*h(t) Impulse Response LTI System f(t) h(t)*f(t)

Properties of Convolution P y y b e v ro s e v l e s r ou

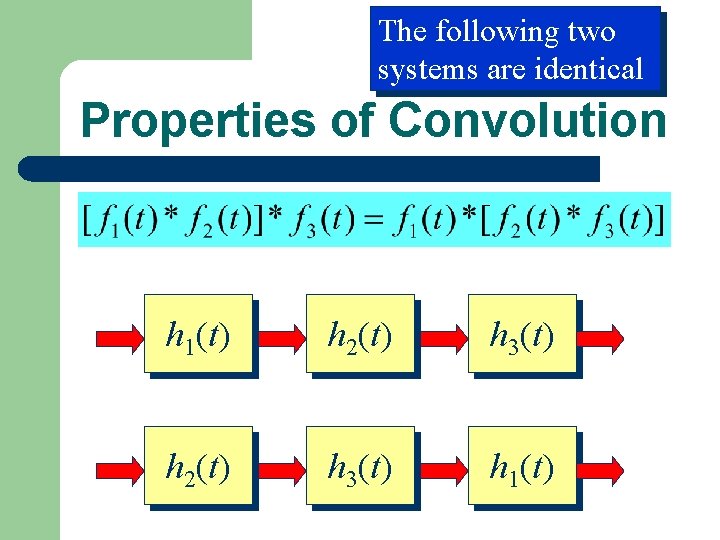
The following two systems are identical Properties of Convolution h 1(t) h 2(t) h 3(t) h 1(t)

Properties of Convolution f(t) f(t)

Properties of Convolution f(t) f(t)

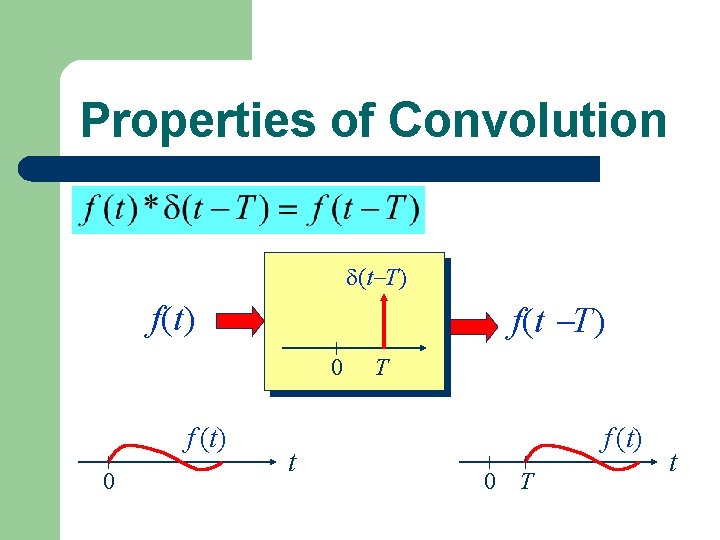
Properties of Convolution (t T) f(t) 0 f (t) 0 t T f (t) 0 T t

System function (t T) serves as an ideal delay or a copier. Properties of Convolution (t T) f(t) 0 f (t) 0 t T f (t) 0 T t

Properties of Convolution

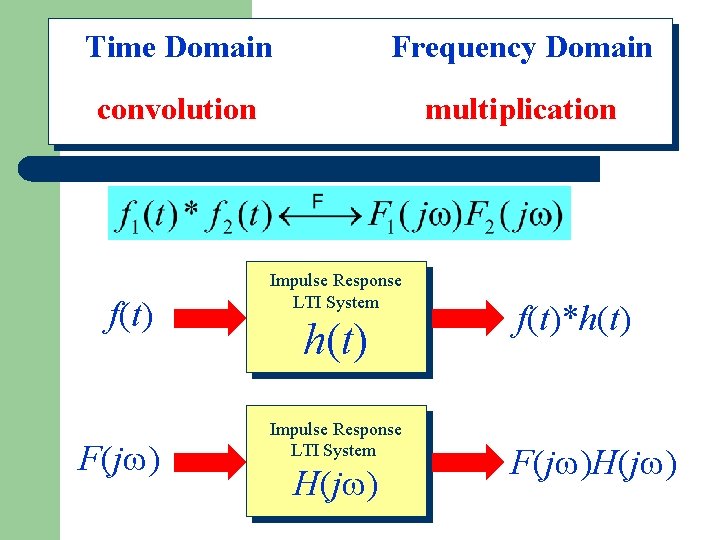
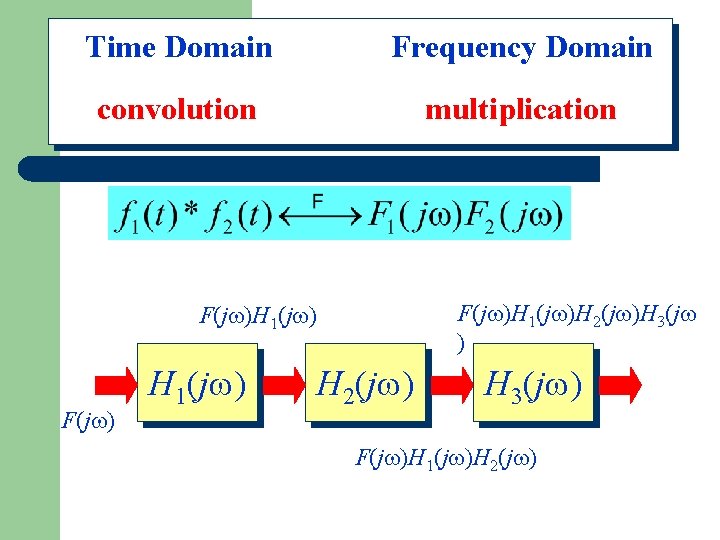
Time Domain Frequency Domain convolution multiplication Properties of Convolution

Time Domain Frequency Domain convolution multiplication Properties of Convolution f(t) F(j ) Impulse Response LTI System h(t) Impulse Response LTI System H(j ) f(t)*h(t) F(j )H(j )

Time Domain Frequency Domain convolution multiplication Properties of Convolution F(j )H 1(j )H 2(j )H 3(j ) F(j )H 1(j ) F(j ) H 1(j ) H 2(j ) H 3(j ) F(j )H 1(j )H 2(j )

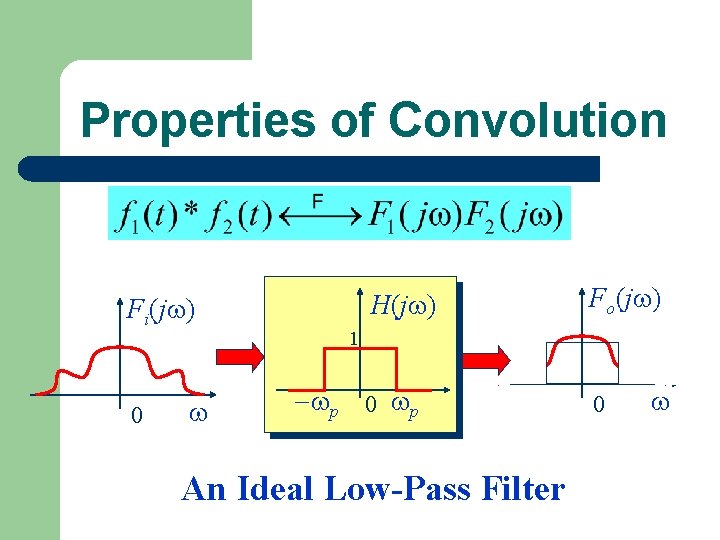
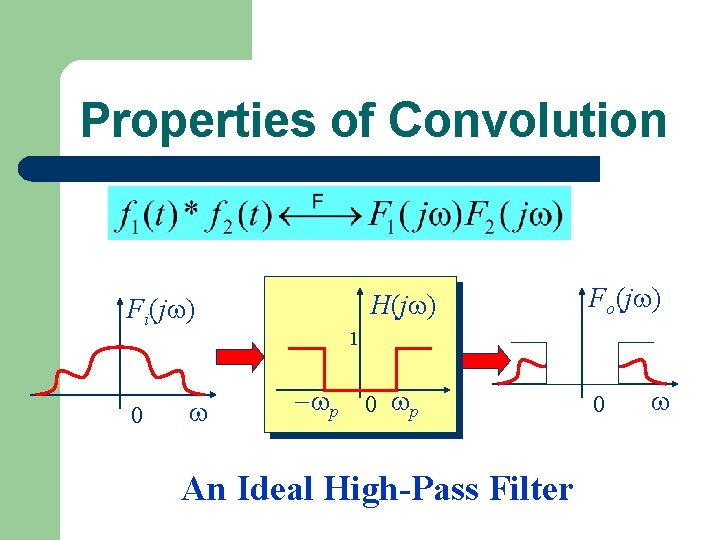
Properties of Convolution Fi(j ) 0 H(j ) Fo(j ) 1 p 0 p An Ideal Low-Pass Filter 0

Properties of Convolution Fi(j ) 0 H(j ) Fo(j ) 1 p 0 p An Ideal High-Pass Filter 0

Properties of Convolution s e v l e s r u o Prove by y

Time Domain multiplication Frequency Domain convolution Properties of Convolution s e v l e s r u o Prove by y

Continuous-Time Fourier Transform Parseval’s Theorem

Properties of Convolution =0

Properties of Convolution If f 1(t) and f 2(t) are real functions, f 2(t) real

Parseval’s Theorem: Energy Preserving
 Introduction to fast fourier transform
Introduction to fast fourier transform Fourier transform of sinc
Fourier transform of sinc Dirac fourier transform
Dirac fourier transform Ctft
Ctft Short time fourier transform
Short time fourier transform Fourier series coefficients formula
Fourier series coefficients formula Parseval's identity for fourier transform
Parseval's identity for fourier transform Fourier transform properties table
Fourier transform properties table Synthesis equation fourier series
Synthesis equation fourier series Fourier transform amplitude and phase
Fourier transform amplitude and phase Discrete fourier transform of delta function
Discrete fourier transform of delta function Matlab ramp function
Matlab ramp function Fourier transform mri
Fourier transform mri Fourier transform properties solved examples
Fourier transform properties solved examples Unit step function fourier transform
Unit step function fourier transform Gaussian fourier transform
Gaussian fourier transform Inverse fourier transform
Inverse fourier transform Equation for fourier transform
Equation for fourier transform Fourier image processing
Fourier image processing 2pift
2pift The fourier transform and its applications
The fourier transform and its applications Inverse fourier transform
Inverse fourier transform Fourier transform
Fourier transform Short time fourier transform
Short time fourier transform Polar fft
Polar fft Fourier transform of product of two functions
Fourier transform of product of two functions Discrete fourier transform
Discrete fourier transform Sinc fourier transform
Sinc fourier transform Fourier series of impulse train
Fourier series of impulse train Discrete fourier transform
Discrete fourier transform Fourier transform of impulse train
Fourier transform of impulse train Fourier transform of circ function
Fourier transform of circ function Duality of fourier transform
Duality of fourier transform Fourier transform definition
Fourier transform definition Fourier transform formula
Fourier transform formula Dirichlet condition for fourier series expansion
Dirichlet condition for fourier series expansion Fourier transform table
Fourier transform table Fourier transform pair
Fourier transform pair Duality of fourier transform
Duality of fourier transform Fourier series half range
Fourier series half range Windowed fourier transform
Windowed fourier transform Fourier transform
Fourier transform Fourier transform notation
Fourier transform notation Relation between laplace and fourier transform
Relation between laplace and fourier transform Fourier transform solver
Fourier transform solver Periodic function fourier transform
Periodic function fourier transform Discrete fourier transform formula
Discrete fourier transform formula Discrete time fourier series
Discrete time fourier series Fftshift
Fftshift Chirped pulse fourier transform microwave spectroscopy
Chirped pulse fourier transform microwave spectroscopy Fourier transform of shifted rectangular pulse
Fourier transform of shifted rectangular pulse Dft
Dft Fourier transform pair
Fourier transform pair Fast fourier transform java
Fast fourier transform java Top hat function fourier transform
Top hat function fourier transform Inverse of fourier transform
Inverse of fourier transform Fractional fourier transform
Fractional fourier transform Fourier transform rules
Fourier transform rules Application of discrete fourier transform
Application of discrete fourier transform Fourier transform seismic
Fourier transform seismic Inverse of fourier transform
Inverse of fourier transform Fourier transform in computer vision
Fourier transform in computer vision Fourier transform complex analysis
Fourier transform complex analysis Ft representation
Ft representation Fourier transform conclusion
Fourier transform conclusion Orthogonality of trigonometric functions
Orthogonality of trigonometric functions Fourier transform
Fourier transform Fourier transform
Fourier transform Fourier transform
Fourier transform