CHAPTER 4 APPLICATIONS OF FOURIER REPRESENTATIONS TO MIXED

CHAPTER 4 APPLICATIONS OF FOURIER REPRESENTATIONS TO MIXED SIGNAL CLASSES • What about the Fourier representation of a mixture of a) periodic and non-periodic signals b) CT and DT signals? Examples:

• We will go through: a) FT of periodic signals, which we have used FS: We can take FT of x(t). b) Convolution and multiplication with mixture of periodic and non-periodic signals. c) Fourier transform of discrete-time signals. FT of periodic signals Chapter 3: for CT periodic signals, FS representations. What happens if we take FT of periodic signals?

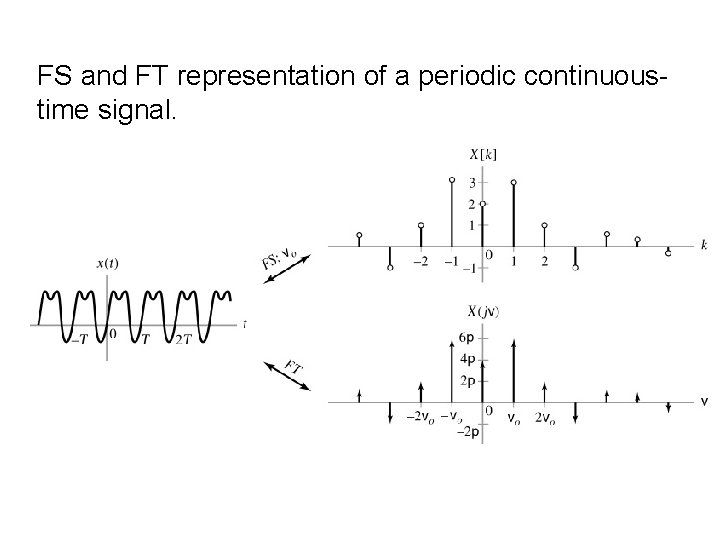
FS representation of periodic signal x(t): Take FT of equation (*) Note: a) FT of a periodic signal is a series of impulses spaced by the fundamental frequency 0. b) The k-th impulse has strength 2 p. X[k]. c) FT of x(t)=cos( 0 t) can be obtained by replacing

FS and FT representation of a periodic continuoustime signal.

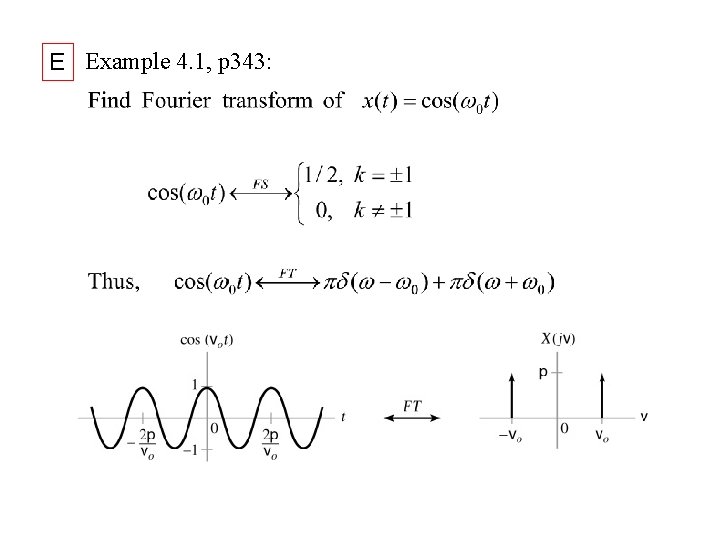
E Example 4. 1, p 343:

E Example 4. 2, p 344: p(t) is periodic with fundamental period T, fundamental frequency 0. FS coefficients:

Relating DTFT to DTFS N-periodic signal x[n] has DTFS expression Extending to any interval: This, DTFT of x[n] given in (*) is expressed as:

Since X[k] is N periodic and NW 0=2 p, we have Note: a) DTFS DTFT: b) DTFT DTFS: Also, replace sum intervals from 0~N-1 for DTFS to - ~ for DTFT E Problem 4. 3(c), p 347: Fundamental period?

Use note a) last slide: Question: if we take inverse DTFS of X[k], we get Exercise: use Matlab to verify.

Convolution and multiplication with mixture of periodic and non-periodic signals For periodic inputs: 1) Convolution of periodic and non-periodic signals

E Problem 4. 4(a), p 350: LTI system has an impulse response

Because h(t) is an ideal bandpass filter with a bandwidth 2 p centered at 4 p, the Fourier transform of the output signal is thus which has a time-domain expression given as: For discrete-time signals:

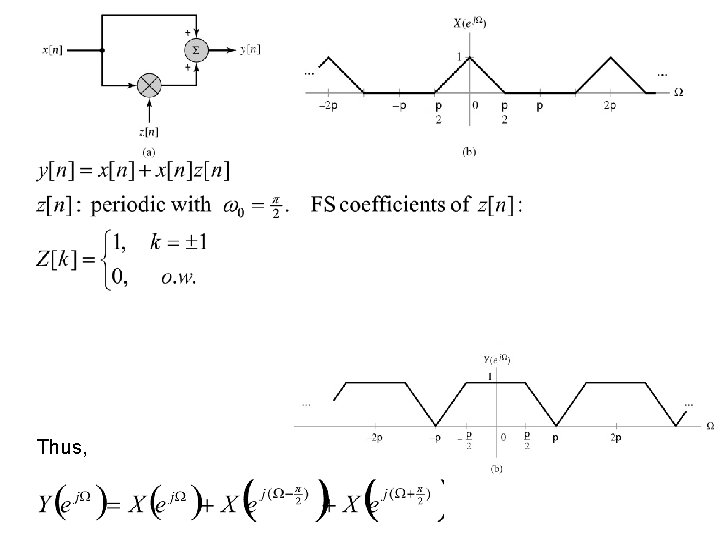
2) Multiplication of periodic and non-periodic signals Carrying out the convolution yields: DT case: E Problem 4. 7, p 357(b): Consider the LTI system and input signal spectrum X(ej. W) depicted by the figure below. Determine an expression for Y(ej. W), the DTFT of the output y[n] assuming that z[n]=2 cos(pn/2).

Thus,

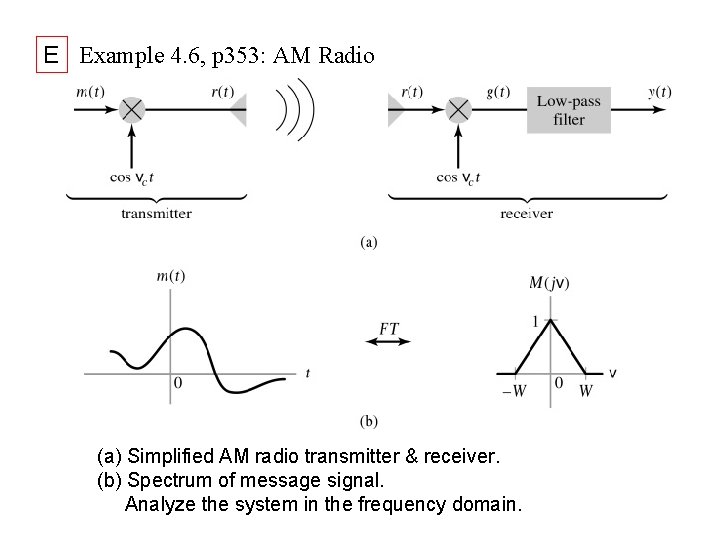
E Example 4. 6, p 353: AM Radio (a) Simplified AM radio transmitter & receiver. (b) Spectrum of message signal. Analyze the system in the frequency domain.

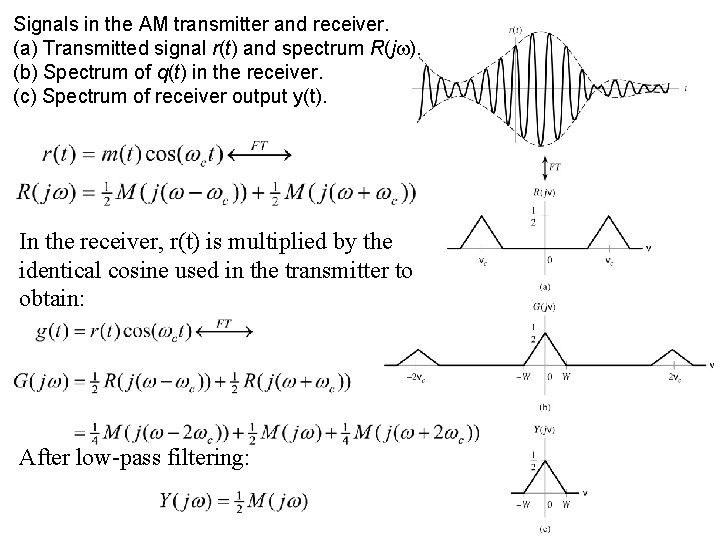
Signals in the AM transmitter and receiver. (a) Transmitted signal r(t) and spectrum R(j ). (b) Spectrum of q(t) in the receiver. (c) Spectrum of receiver output y(t). In the receiver, r(t) is multiplied by the identical cosine used in the transmitter to obtain: After low-pass filtering: