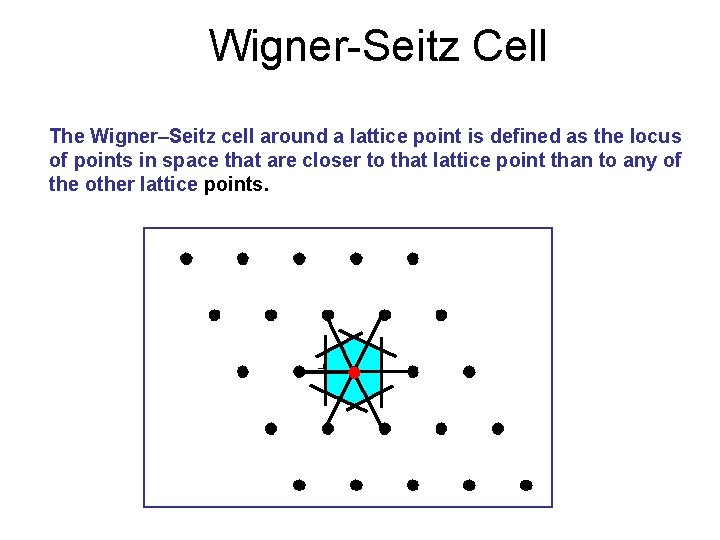
WignerSeitz Cell The WignerSeitz cell around a lattice



![Examples 210 X=½ , Y=½, Z=1 [½ ½ 1] [1 1 2] X=1, Y=½, Examples 210 X=½ , Y=½, Z=1 [½ ½ 1] [1 1 2] X=1, Y=½,](https://slidetodoc.com/presentation_image/1de2ed66fc9820079d630f082e016ccf/image-9.jpg)
![Negative directions • When we write the direction [n 1 n 2 n 3] Negative directions • When we write the direction [n 1 n 2 n 3]](https://slidetodoc.com/presentation_image/1de2ed66fc9820079d630f082e016ccf/image-10.jpg)
![Examples of crystal directions X=1, Y=0, Z=0 [1 0 0] X = -1 , Examples of crystal directions X=1, Y=0, Z=0 [1 0 0] X = -1 ,](https://slidetodoc.com/presentation_image/1de2ed66fc9820079d630f082e016ccf/image-11.jpg)



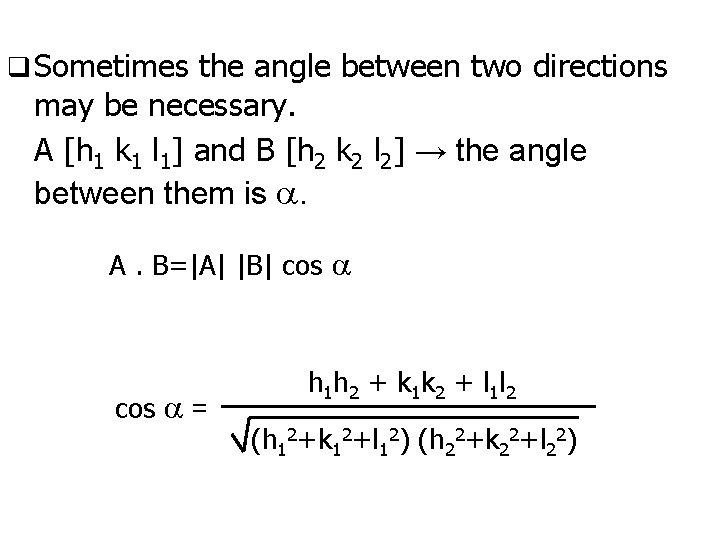



- Slides: 32

Wigner-Seitz Cell The Wigner–Seitz cell around a lattice point is defined as the locus of points in space that are closer to that lattice point than to any of the other lattice points.

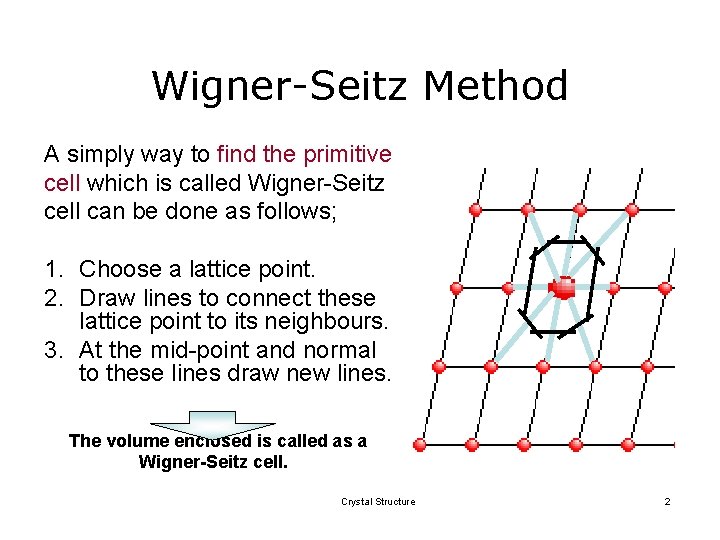
Wigner-Seitz Method A simply way to find the primitive cell which is called Wigner-Seitz cell can be done as follows; 1. Choose a lattice point. 2. Draw lines to connect these lattice point to its neighbours. 3. At the mid-point and normal to these lines draw new lines. The volume enclosed is called as a Wigner-Seitz cell. Crystal Structure 2

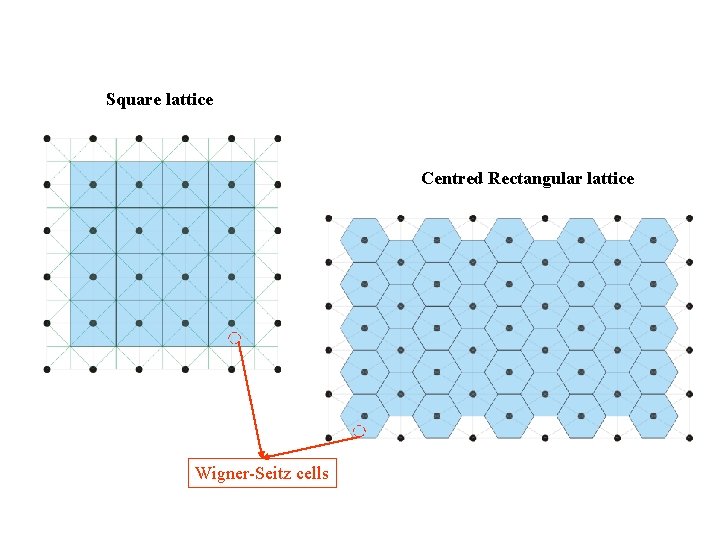
Square lattice Centred Rectangular lattice Wigner-Seitz cells

Different kinds of CELLS Unit cell A unit cell is a spatial arrangement of atoms which is tiled in three-dimensional space to describe the crystal. Primitive unit cell For each crystal structure there is a conventional unit cell, usually chosen to make the resulting lattice as symmetric as possible. However, the conventional unit cell is not always the smallest possible choice. A primitive unit cell of a particular crystal structure is the smallest possible unit cell one can construct such that, when tiled, it completely fills space. Wigner-Seitz cell A Wigner-Seitz cell is a particular kind of primitive cell which has the same symmetry as the lattice.

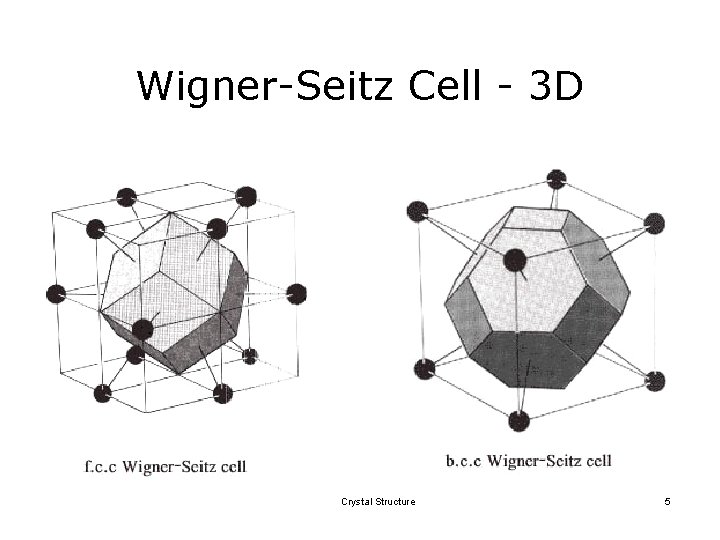
Wigner-Seitz Cell - 3 D Crystal Structure 5

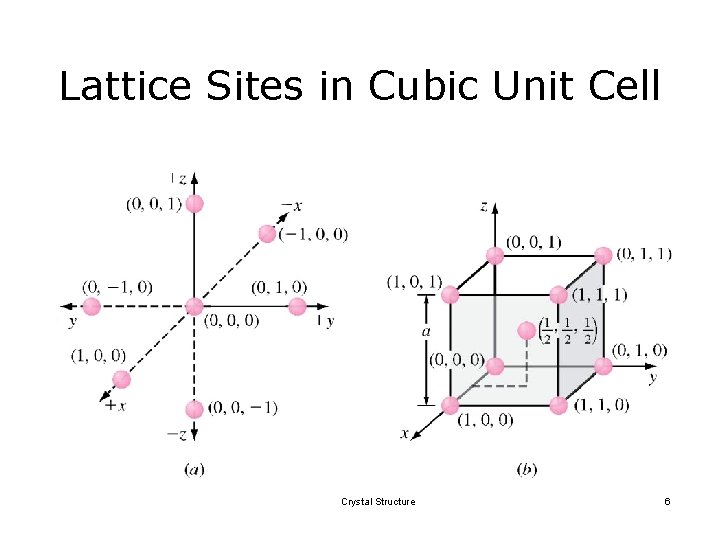
Lattice Sites in Cubic Unit Cell Crystal Structure 6

Lecture 03 CRYSTALLOGRAPHIC POINTS, DIRECTIONS, PLANES & THE MILLER SYSTEM OF INDICES Fundamental properties of Solids

Crystal Directions • • We choose one lattice point on the line as an origin, say the point O. Choice of origin is completely arbitrary, since every lattice point is identical. Then we choose the lattice vector joining O to any point on the line, say point T. This vector can be written as; R = n 1 a + n 2 b + n 3 c • • To distinguish a lattice direction from a lattice point, the triple is enclosed in square brackets [. . . ] is used. [n 1 n 2 n 3] is the smallest integer of the same relative ratios. Crystal Structure Fig. Shows [111] direction 8
![Examples 210 X½ Y½ Z1 ½ ½ 1 1 1 2 X1 Y½ Examples 210 X=½ , Y=½, Z=1 [½ ½ 1] [1 1 2] X=1, Y=½,](https://slidetodoc.com/presentation_image/1de2ed66fc9820079d630f082e016ccf/image-9.jpg)
Examples 210 X=½ , Y=½, Z=1 [½ ½ 1] [1 1 2] X=1, Y=½, Z=0 [1 ½ 0] [2 1 0] Crystal Structure 9
![Negative directions When we write the direction n 1 n 2 n 3 Negative directions • When we write the direction [n 1 n 2 n 3]](https://slidetodoc.com/presentation_image/1de2ed66fc9820079d630f082e016ccf/image-10.jpg)
Negative directions • When we write the direction [n 1 n 2 n 3] depend on the origin, negative directions can be written as Z direction (origin) O • R = n 1 a + n 2 b + n 3 c Direction must be smallest integers. - X direction - Y direction X direction - Z direction Crystal Structure 10
![Examples of crystal directions X1 Y0 Z0 1 0 0 X 1 Examples of crystal directions X=1, Y=0, Z=0 [1 0 0] X = -1 ,](https://slidetodoc.com/presentation_image/1de2ed66fc9820079d630f082e016ccf/image-11.jpg)
Examples of crystal directions X=1, Y=0, Z=0 [1 0 0] X = -1 , Y = -1 , Z = 0 Crystal Structure [110] 11

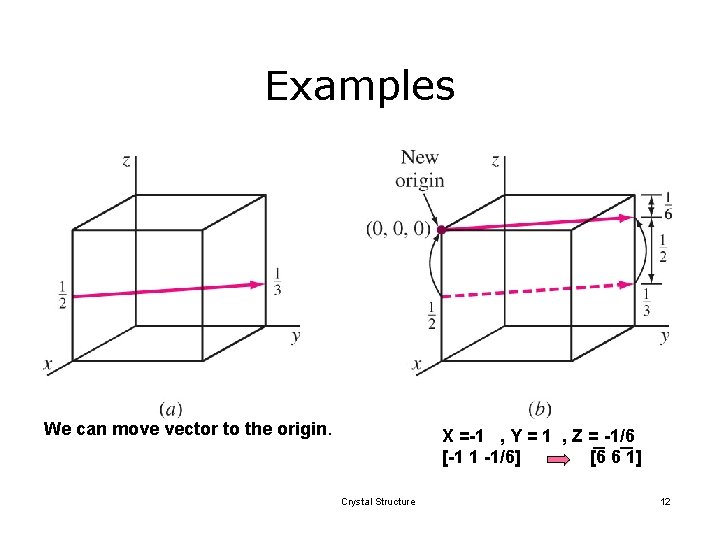
Examples We can move vector to the origin. X =-1 , Y = 1 , Z = -1/6 [-1 1 -1/6] [6 6 1] Crystal Structure 12

q When dealing with crsytalline materials, it is often necessary to specify a particular point within a unit cell, a particular direction or a particular plane of atoms. q Planes are important in crystals because if bonding is weak between a set of parallel planes, then brittle shear fracture may occur along these planes. q Therefore, it is necessary to be able to specify individual crystal planes and in the case of shear to specify directions within these planes. Such identification is carried out by means of Miller Indices.

CRYSTALLOGRAPHIC DIRECTIONS A crystallographic direction is defined as a line between two points (a vector). 1. A vector of convenient length is positioned such that it passes through the origin of the coordinate system. (Any vector can be translated throughout the crystal lattice, if parallelism is maintained). 2. The length of the vector projection on each of the three axes is determined in terms of the unit cell dimensions a, b, and c. 3. These three numbers are multiplied or divided by a common factor to reduce them to the smallest integer values. 4. The tree indices are enclosed in brackets as [uvw]. The u, v, and w integers correspond to the reduced projections along x, y, and z-axes respectively.

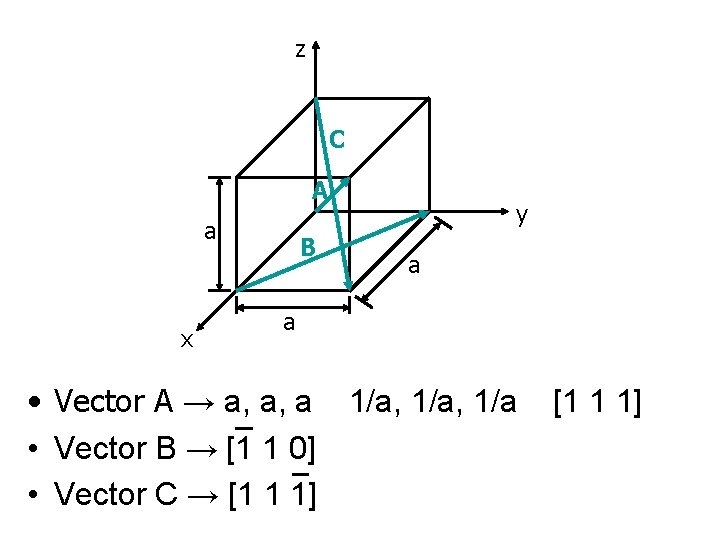
z C A a x B y a a • Vector A → a, a, a 1/a, 1/a [1 1 1] • Vector B → [1 1 0] • Vector C → [1 1 1]

• For some crystal structures, several nonparallel directions with different indices are actually equivalent. (The spacing of atoms along each direction is the same) • For example in cubic crystals, all the directions represented by the following indices are equivalent. • As a convenience, equivalent directions are grouped into a “family” which are grouped in angle brackets.
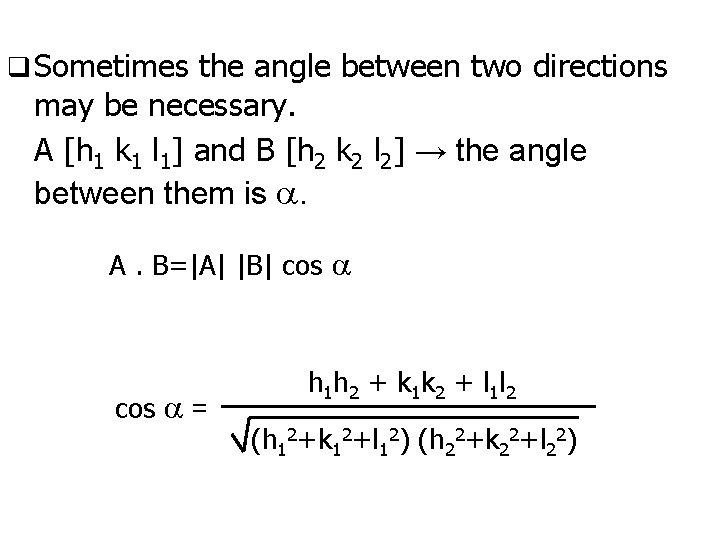
q Sometimes the angle between two directions may be necessary. A [h 1 k 1 l 1] and B [h 2 k 2 l 2] → the angle between them is a. A. B=|A| |B| cos a = h 1 h 2 + k 1 k 2 + l 1 l 2 (h 12+k 12+l 12) (h 22+k 22+l 22)

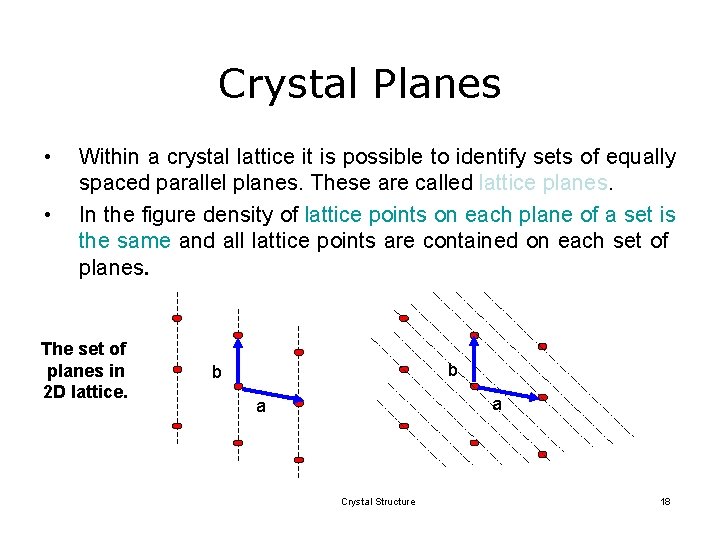
Crystal Planes • • Within a crystal lattice it is possible to identify sets of equally spaced parallel planes. These are called lattice planes. In the figure density of lattice points on each plane of a set is the same and all lattice points are contained on each set of planes. The set of planes in 2 D lattice. b b a a Crystal Structure 18

CRYSTALLOGRAPHIC PLANES • The orientations of planes for a crystal structure are represented in a similar manner. • In all but the hexagonal crystal system, crystallographic planes are specified by three Miller Indices as (hkl). • Any two parallel planes are equivalent and have identical indices. • The following procedure is employed in the determining the h, k, and l idex numbers of a plane:

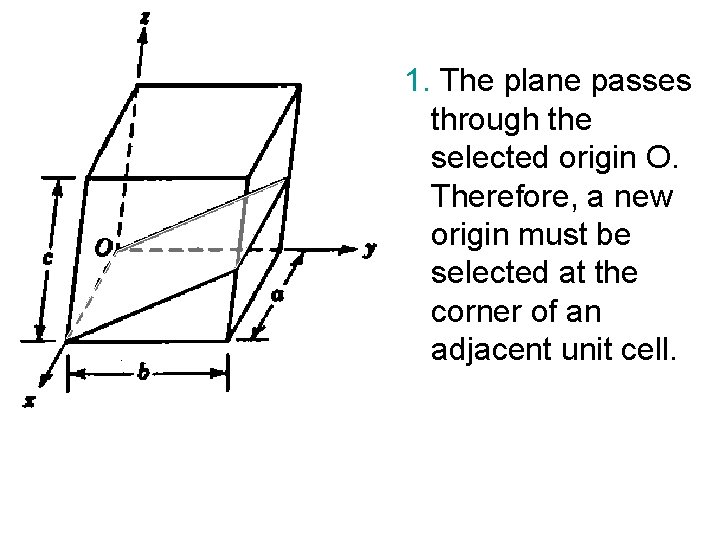
1. If the plane passes through the selected origin, either another parallel plane must be constructed within the unit cell by an appropriate translation, or a new origin must be established at the corner of another unit cell. 2. At this point the crystallographic plane either intersects or parallels each of the three axes; the length of the planar intercept for each axis is determined in terms of the lattice parameters a, b, and c. 3. The reciprocals of these numbers are taken. 4. If necessary, these three numbers are changed to the set of smallest integers by multiplication or division by a common factor. 5. The integer indices are enclosed within parantheses as (hkl).

1. The plane passes through the selected origin O. Therefore, a new origin must be selected at the corner of an adjacent unit cell.


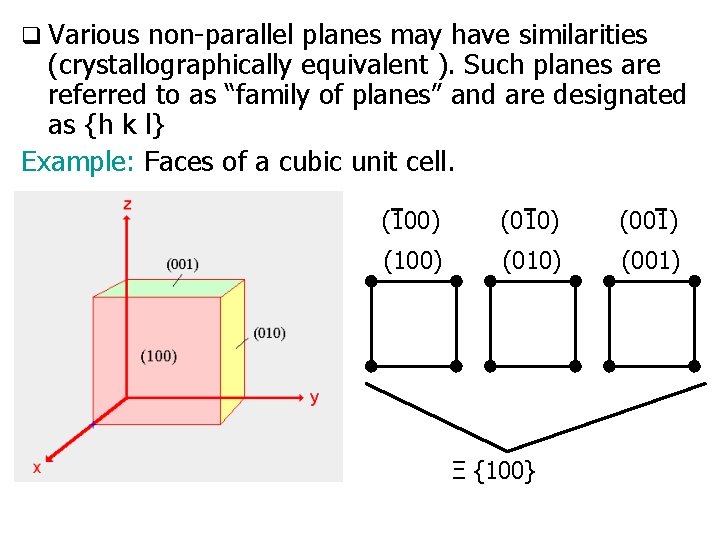
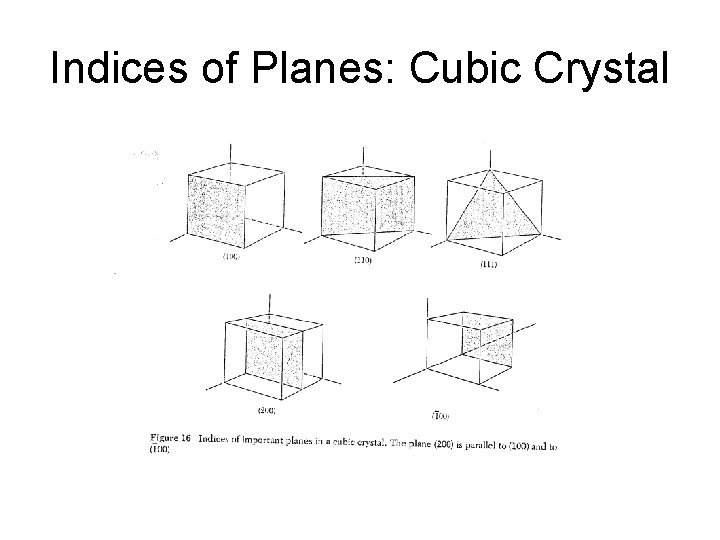
q Various non-parallel planes may have similarities (crystallographically equivalent ). Such planes are referred to as “family of planes” and are designated as {h k l} Example: Faces of a cubic unit cell. (100) (010) (001) Ξ {100}

Indices of Planes: Cubic Crystal

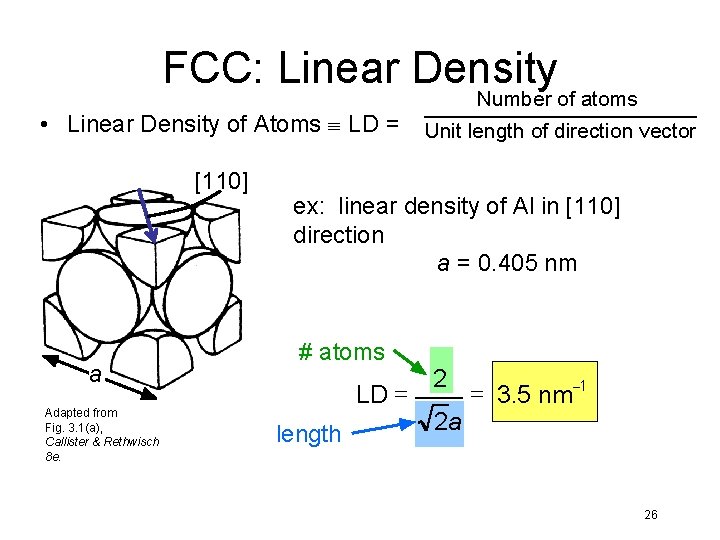
LINEAR DENSITY q When planes slip over each other, slip takes place in the direction of closest packing of atoms on the planes. q The linear density of a crystal direction [h k l] is determined as: δ[h k l] = # of atoms length

FCC: Linear Density Number of atoms • Linear Density of Atoms LD = Unit length of direction vector [110] a Adapted from Fig. 3. 1(a), Callister & Rethwisch 8 e. ex: linear density of Al in [110] direction a = 0. 405 nm # atoms LD = length 2 2 a = 3. 5 nm-1 26

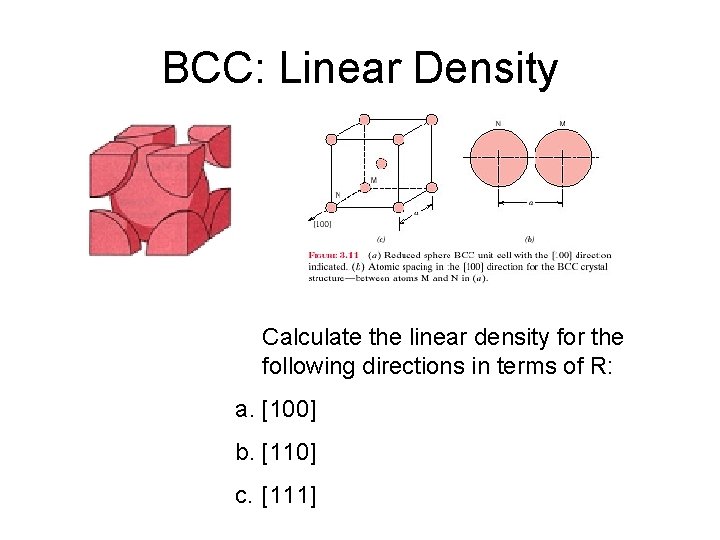
BCC: Linear Density Calculate the linear density for the following directions in terms of R: a. [100] b. [110] c. [111]

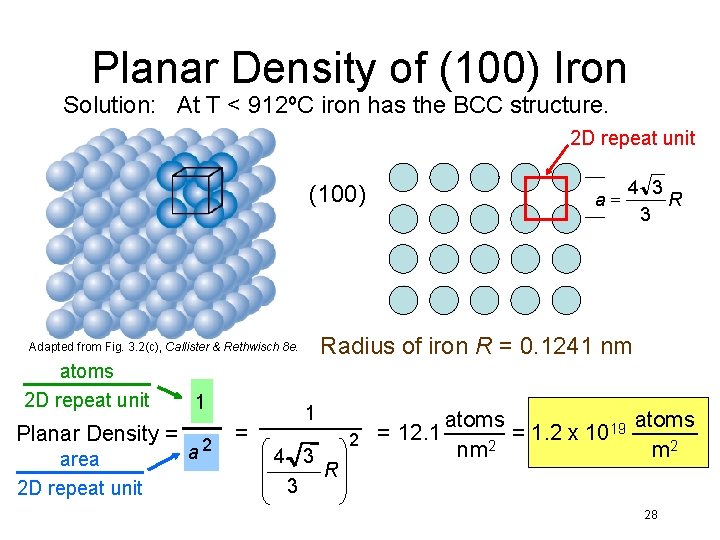
Planar Density of (100) Iron Solution: At T < 912ºC iron has the BCC structure. 2 D repeat unit (100) 1 Planar Density = 2 a area 2 D repeat unit = 4 3 Radius of iron R = 0. 1241 nm Adapted from Fig. 3. 2(c), Callister & Rethwisch 8 e. atoms 2 D repeat unit a= 1 4 3 R 3 atoms 19 = 1. 2 x 10 2 = 12. 1 2 nm m 2 28

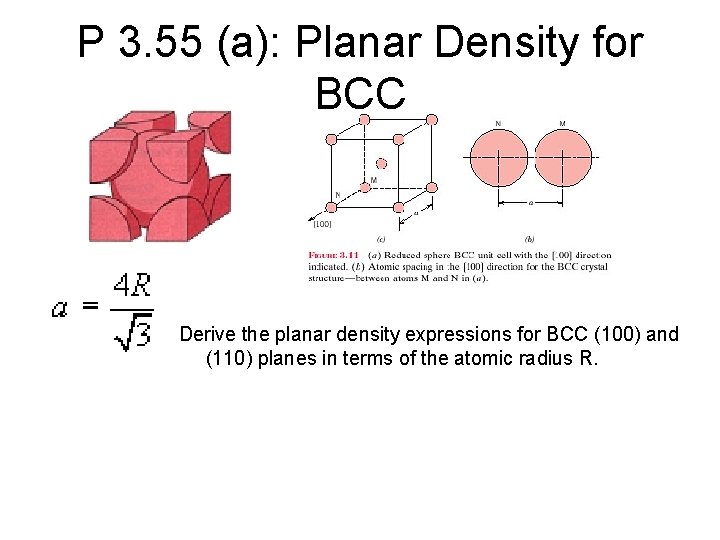
P 3. 55 (a): Planar Density for BCC Derive the planar density expressions for BCC (100) and (110) planes in terms of the atomic radius R.

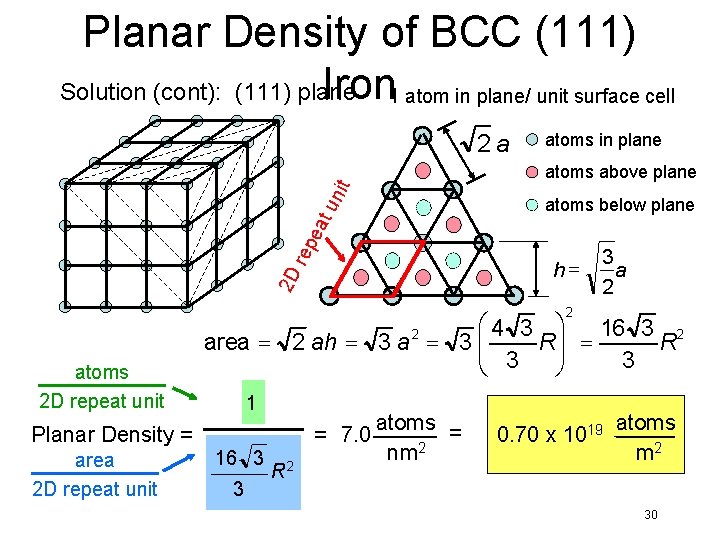
Planar Density of BCC (111) Iron 1 atom in plane/ unit surface cell Solution (cont): (111) plane 2 a atoms in plane un it atoms above plane re pe at atoms below plane 2 D h= 3 a 2 2 atoms 2 D repeat unit Planar Density = area 2 D repeat unit æ 4 3 ö 16 3 2 2 area = 2 ah = 3 a = 3 çç R = R 3 è 3 ø 1 16 3 3 = 7. 0 R 2 atoms = nm 2 0. 70 x 1019 atoms m 2 30

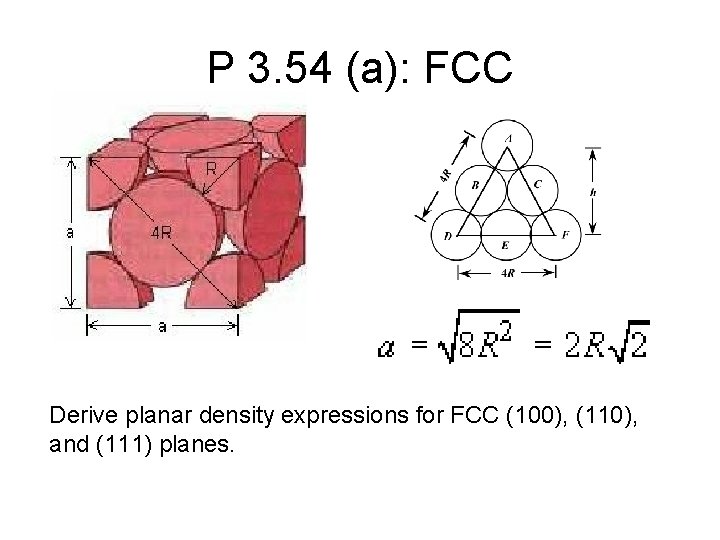
P 3. 54 (a): FCC Derive planar density expressions for FCC (100), (110), and (111) planes.

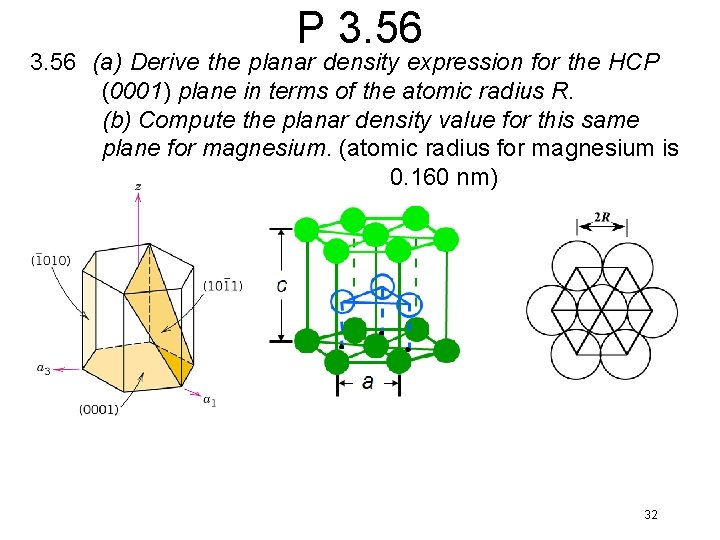
P 3. 56 (a) Derive the planar density expression for the HCP (0001) plane in terms of the atomic radius R. (b) Compute the planar density value for this same plane for magnesium. (atomic radius for magnesium is 0. 160 nm) 32