Lattice Convertible Bondwithcallable function price lattice Lattice Convertible

![Lattice. Convertible. Bondwithcallable function [price, lattice] = Lattice. Convertible. Bondwithcallable(S 0, r, rc, FV, Lattice. Convertible. Bondwithcallable function [price, lattice] = Lattice. Convertible. Bondwithcallable(S 0, r, rc, FV,](http://slidetodoc.com/presentation_image/cc433d2d3544ce4d04f3c46c3b2196cd/image-2.jpg)
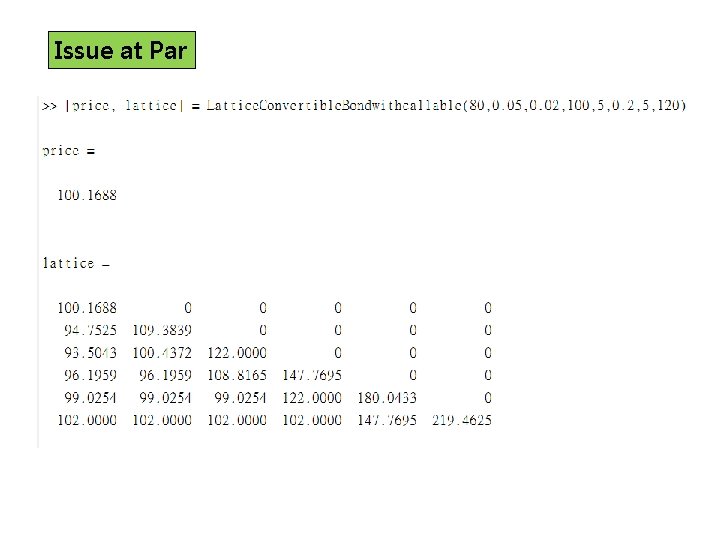
Lattice. Convertible. Bondwithcallable function [price, lattice] = Lattice. Convertible. Bondwithcallable(S 0, r, rc, FV, T, sigma, N, callable) delta. T = T/N; u=exp(sigma * sqrt(delta. T)); d=1/u; p=(exp(r*delta. T) - d)/(u-d); lattice = zeros(N+1, N+1); ST = zeros(N+1, N+1); for j=0: N lattice(N+1, j+1)=max(min(FV , callable) , S 0*(u^j)*(d^(N-j)))+rc*FV; end for i=N-1: 0 for j=0: i lattice(i+1, j+1) = max( min(exp(-r*delta. T) * (p * lattice(i+2, j+2) + (1 -p) * lattice(i+2, j+1)) , callable) , S 0*u^j*d^(i-j) )+rc*FV; end price = lattice(1, 1);

plot. Lattice. CBwithcallable S 0=80; r=0. 05; rc=0. 02; FV=100; T=5; sigma=0. 2; N=5; for callable=60: 1: 150 [price, lattice] = Lattice. Convertible. Bondwithcallable(S 0, r, rc, FV, T, sigma, N, callable); plot(callable, price, 'r. -'); hold on; end title('Lattice. CBwithcallable'); xlabel('callable price'); ylabel('issue price');

Issue at Par
![UOCall. MC UOCall % UOCall. MC. m function [C, CI, NCrossed] = UOCall. MC(S UOCall. MC UOCall % UOCall. MC. m function [C, CI, NCrossed] = UOCall. MC(S](http://slidetodoc.com/presentation_image/cc433d2d3544ce4d04f3c46c3b2196cd/image-6.jpg)
UOCall. MC UOCall % UOCall. MC. m function [C, CI, NCrossed] = UOCall. MC(S 0, X, r, T, sigma, Sb, NSteps, NRepl) % Generate asset paths Payoff = zeros(NRepl, 1); NCrossed = 0; for i=1: NRepl Path=Asset. Paths 1(S 0, r, sigma, T, NSteps, 1); crossed = any(Path >= Sb); if crossed == 0 Payoff(i) = max(0, Path(NSteps+1)-X); else Payoff(i) = 0; NCrossed = NCrossed + 1; end [C, aux, CI] = normfit( exp(-r*T) * Payoff);
![UOCall. MCCond function [Cuo, CI, NCrossed] = UOCall. MCCond(S 0, X, r, T, sigma, UOCall. MCCond function [Cuo, CI, NCrossed] = UOCall. MCCond(S 0, X, r, T, sigma,](http://slidetodoc.com/presentation_image/cc433d2d3544ce4d04f3c46c3b2196cd/image-7.jpg)
UOCall. MCCond function [Cuo, CI, NCrossed] = UOCall. MCCond(S 0, X, r, T, sigma, Sb, NSteps, NRepl) dt = T/NSteps; [Call, Put] = blsprice(S 0, X, r, T, sigma); % Generate asset paths and payoffs for the up and in option NCrossed = 0; Payoff = zeros(NRepl, 1); Times = zeros(NRepl, 1); Stock. Vals = zeros(NRepl, 1); for i=1: NRepl Path=Asset. Paths 1(S 0, r, sigma, T, NSteps, 1); tcrossed = min(find( Path >= Sb )); if not(isempty(tcrossed)) NCrossed = NCrossed + 1; Times(NCrossed) = (tcrossed-1) * dt; Stock. Vals(NCrossed) = Path(tcrossed); end if (NCrossed > 0) [Caux, Paux] = blsprice(Stock. Vals(1: NCrossed), X, r, T-Times(1: NCrossed), sigma); Payoff(1: NCrossed) = exp(-r*Times(1: NCrossed)). * Caux; end [Cuo, aux, CI] = normfit(Call - Payoff);
![UOCall. MCCond. IS % UOCall. MCCond. IS. m function [Cuo, CI, NCrossed] =. . UOCall. MCCond. IS % UOCall. MCCond. IS. m function [Cuo, CI, NCrossed] =. .](http://slidetodoc.com/presentation_image/cc433d2d3544ce4d04f3c46c3b2196cd/image-8.jpg)
UOCall. MCCond. IS % UOCall. MCCond. IS. m function [Cuo, CI, NCrossed] =. . . UOCall. MCCond. IS(S 0, X, r, T, sigma, Sb, NSteps, NRepl, bp) dt = T/NSteps; nudt = (r-0. 5*sigma^2)*dt; b = bp*nudt; sidt = sigma*sqrt(dt); [Call, Put] = blsprice(S 0, X, r, T, sigma); % Generate asset paths and payoffs for the up and in option NCrossed = 0; Payoff = zeros(NRepl, 1); Times = zeros(NRepl, 1); Stock. Vals = zeros(NRepl, 1); ISRatio = zeros(NRepl, 1);

for i=1: NRepl % generate normals vet. Z = nudt - b + sidt*randn(1, NSteps); Log. Path = cumsum([log(S 0), vet. Z]); Path = exp(Log. Path); jcrossed = min(find( Path >= Sb )); if not(isempty(jcrossed)) NCrossed = NCrossed + 1; TBreach = jcrossed - 1; Times(NCrossed) = TBreach * dt; Stock. Vals(NCrossed) = Path(jcrossed); ISRatio(NCrossed) = exp( TBreach*b^2/2/sigma^2/dt +. . . b/sigma^2/dt*sum(vet. Z(1: TBreach)) -. . . TBreach*b/sigma^2*(r - sigma^2/2)); end if (NCrossed > 0) [Caux, Paux] = blsprice(Stock. Vals(1: NCrossed), X, r, . . . T-Times(1: NCrossed), sigma); Payoff(1: NCrossed) = exp(-r*Times(1: NCrossed)). * Caux. . * ISRatio(1: NCrossed); end [Cuo, aux, CI] = normfit(Call - Payoff);

Comp. UOCall. MCCond. IS % Comp. UOCall. MCCond. IS. m Compare UOCall. MC, MCcond clear S 0=50; X=52; r=0. 1; T=2/12; sigma=0. 4; Sb 1=80*exp(+0. 5826*0. 4*sqrt(1/12/30)); Sb 2=80; NStep=60; NRepl=10000; bp 0=0; bp 20=-20; bp 50=-50; bp 200=-200;

UOCalldiscrete=UOCall(S 0, X, r, T, sigma, Sb 1); randn('seed', 0); [UOCall. MC, CI 1, NCrossed 1]=UOCall. MC(S 0, X, r, T, sigma, Sb 2, NStep, NRepl); randn('seed', 0); [UOCall. MCCond, CI 2, NCrossed 2]=UOCall. MCCond(S 0, X, r, T, sigma, Sb 2, NStep, NRepl); randn('seed', 0); [UOCall. MCCond. IS 0, CI 3, NCrossed 3]=UOCall. MCCond. IS(S 0, X, r, T, sigma, Sb 2, N Step, NRepl, bp 0); randn('seed', 0); [UOCall. MCCond. IS 20, CI 4, NCrossed 4]=UOCall. MCCond. IS(S 0, X, r, T, sigma, Sb 2, NStep, NRepl, bp 20); randn('seed', 0); [UOCall. MCCond. IS 50, CI 5, NCrossed 5]=UOCall. MCCond. IS(S 0, X, r, T, sigma, Sb 2, NStep, NRepl, bp 50); randn('seed', 0); [UOCall. MCCond. IS 200, CI 6, NCrossed 6]=UOCall. MCCond. IS(S 0, X, r, T, sigma, Sb 2, NStep, NRepl, bp 200);

UOCalldiscrete UOCall. MC CI 1 NCrossed 1 UOCall. MCCond CI 2 NCrossed 2 UOCall. MCCond. IS 0 CI 3 NCrossed 3 UOCall. MCCond. IS 20 CI 4 NCrossed 4 UOCall. MCCond. IS 50 CI 5 NCrossed 5 UOCall. MCCond. IS 200 CI 6 NCrossed 6

- Slides: 13