Examples Lattice Construction and Lattice Traversal Examples Verification

  • Slides: 16
Download presentation
Examples Lattice Construction and Lattice Traversal Examples

Examples Lattice Construction and Lattice Traversal Examples

Verification of Code with Library Functions • int main(void) { int x = 45;

Verification of Code with Library Functions • int main(void) { int x = 45; int y = 18; int g = gcd(x, y); assert(g <= x); } int gcd(int x, int y) { int tmp; while (y!=0){ tmp = x%y; x = y; y = tmp; } return x; } 2

Refinement via Lattice of a Function • The model: o 3 facts of modulo

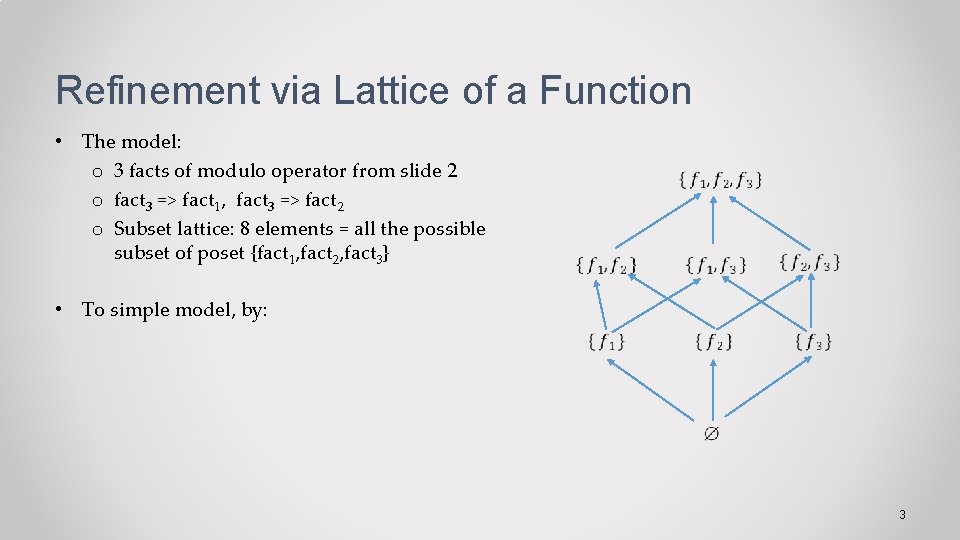
Refinement via Lattice of a Function • The model: o 3 facts of modulo operator from slide 2 o fact 3 => fact 1, fact 3 => fact 2 o Subset lattice: 8 elements = all the possible subset of poset {fact 1, fact 2, fact 3} • To simple model, by: 3

Refinement via Lattice of a Function • The model: o 3 facts of modulo

Refinement via Lattice of a Function • The model: o 3 facts of modulo operator from slide 2 o fact 3 => fact 1, fact 3 => fact 2 o Subset lattice: 8 elements = all the possible subset of poset {fact 1, fact 2, fact 3} • To simple model, by: o Remove Contradictions: fact 1 + fact 2 is false 3

Refinement via Lattice of a Function • The model: o 3 facts of modulo

Refinement via Lattice of a Function • The model: o 3 facts of modulo operator from slide 2 o fact 3 => fact 1, fact 3 => fact 2 o Subset lattice: 8 elements = all the possible subset of poset {fact 1, fact 2, fact 3} • To simple model, by: o Remove Contradictions: fact 1 + fact 2 is false o Remove Duplications: fact 3 to replace the rest 3

Refinement via Lattice of a Function • The model: o 3 facts of modulo

Refinement via Lattice of a Function • The model: o 3 facts of modulo operator from slide 2 o fact 3 => fact 1, fact 3 => fact 2 o Subset lattice: 8 elements = all the possible subset of poset {fact 1, fact 2, fact 3} • To simple model, by: o Remove Contradictions: fact 1 + fact 2 is false o Remove Duplications: fact 3 to replace the rest 3

Refinement via Lattice of a Function • The model: o 3 facts of modulo

Refinement via Lattice of a Function • The model: o 3 facts of modulo operator from slide 2 o fact 3 => fact 1, fact 3 => fact 2 o Subset lattice: 8 elements = all the possible subset of poset {fact 1, fact 2, fact 3} • To simple model, by: o Remove Contradictions: fact 1 + fact 2 is false o Remove Duplications: fact 3 to replace the rest • Output: New semilattice that is a reduced lattice of the original subset lattice 3

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA lattices (traversal order: L 2, L 1) first mod second mod 1 = {}, mod 2 = {} Result: Note: traversal according to general version + optimization for different occurrences of the same function. Additional optimizations are in the paper. int gcd(int x, int y) { int tmp; while (y!=0){ tmp = x%y; x = y; y = tmp; } return x; } int main(void) { int x = 45; int y = 18; int g = gcd(x, y); assert(g <= x); } 4

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA lattices (traversal order: L 2, L 1) first mod second mod 1 = {f 1}, mod 2 = {f 1} Note: traversal according to general version + optimization for different occurrences of the same function. Additional optimizations are in the paper. int gcd(int x, int y) { int tmp; while (y!=0){ tmp = x%y; x = y; y = tmp; } return x; } int main(void) { int x = 45; int y = 18; int g = gcd(x, y); assert(g <= x); } 4

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA lattices (traversal order: L 2, L 1) first mod second mod 1 = {}, mod 2 = {} Result: SAT CEX: x 1=45, y 1=18, tmp 1=50, x 2=18, y 2=50, tmp 2=40, x 3=50, y 3=40 Note: traversal according to general version + optimization for different occurrences of the same function. Additional optimizations are in the paper. int gcd(int x, int y) { int tmp; while (y!=0){ tmp = x%y; x = y; y = tmp; } return x; } int main(void) { int x = 45; int y = 18; int g = gcd(x, y); assert(g <= x); } 4

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA lattices (traversal order: L 2, L 1) first mod second mod 1 = {f 1}, mod 2 = {f 1} Result: UNSAT Note: UNSAT when called from main with x=45, y=18, not in general! Note: traversal according to general version + optimization for different occurrences of the same function. Additional optimizations are in the paper. int gcd(int x, int y) { int tmp; while (y!=0){ tmp = x%y; x = y; y = tmp; } return x; } int main(void) { int x = 45; int y = 18; int g = gcd(x, y); assert(g <= x); } 4

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA lattices (traversal order: L 2, L 1) first mod second mod 1 = {}, mod 2 = {f 1} Try now the other successor of ⊥ of L 1 (of operator mod 1) Note: traversal according to general version + optimization for different occurrences of the same function. Additional optimizations are in the paper. int gcd(int x, int y) { int tmp; while (y!=0){ tmp = x%y; x = y; y = tmp; } return x; } int main(void) { int x = 45; int y = 18; int g = gcd(x, y); assert(g <= x); } 4

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA lattices (traversal order: L 2, L 1) first mod second mod 1 = {f 2}, mod 2 = {f 1} Note: traversal according to general version + optimization for different occurrences of the same function. Additional optimizations are in the paper. int gcd(int x, int y) { int tmp; while (y!=0){ tmp = x%y; x = y; y = tmp; } return x; } int main(void) { int x = 45; int y = 18; int g = gcd(x, y); assert(g <= x); } 4

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA lattices (traversal order: L 2, L 1) first mod second mod 1 = {f 2}, mod 2 = {f 1} Result: SAT CEX: x 1=45, y 1=18, tmp 1=50, x 2=18, y 2=50, tmp 2=60, x 3=50, y 3=60 Note: traversal according to general version + optimization for different occurrences of the same function. Additional optimizations are in the paper. int gcd(int x, int y) { int tmp; while (y!=0){ tmp = x%y; x = y; y = tmp; } return x; } int main(void) { int x = 45; int y = 18; int g = gcd(x, y); assert(g <= x); } 4

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA lattices (traversal order: L 2, L 1) first mod second mod mod 1 = {f 3}, mod 2 = {f 3} Note: traversal according to general version + optimization for different occurrences of the same function. Additional optimizations are in the paper. int gcd(int x, int y) { int tmp; while (y!=0){ tmp = x%y; x = y; y = tmp; } return x; } int main(void) { int x = 45; int y = 18; int g = gcd(x, y); assert(g <= x); } 4

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA

Lattice Traversal for N=2 • gcd with constants • two modulo op. 2 LRA lattices (traversal order: L 2, L 1) first mod second mod mod 1 = {f 3}, mod 2 = {f 3} Result: UNSAT Note: traversal according to general version + optimization for different occurrences of the same function. Additional optimizations are in the paper. int gcd(int x, int y) { int tmp; while (y!=0){ tmp = x%y; x = y; y = tmp; } return x; } int main(void) { int x = 45; int y = 18; int g = gcd(x, y); assert(g <= x); } 4

UCM Path Traversal UCM Scenarios and Path TraversalUCM Path Traversal UCM Scenarios and Path Traversal
StructureShy Programming Ahmed Traversal StructureShy Programming Traversal StrategyStructureShy Programming Ahmed Traversal StructureShy Programming Traversal Strategy
Tree Traversal Pre Order Tree Traversal 1 VisitTree Traversal Pre Order Tree Traversal 1 Visit
Binary Tree Traversal Methods In a traversal ofBinary Tree Traversal Methods In a traversal of
Tree Traversal Techniques Heaps Tree Traversal Concept TreeTree Traversal Techniques Heaps Tree Traversal Concept Tree
Algoritma Traversal di dalam Graf Traversal di dalamAlgoritma Traversal di dalam Graf Traversal di dalam
Inorder Traversal Inorder traversal Visit the left subtreeInorder Traversal Inorder traversal Visit the left subtree
Binary Tree Traversal Methods In a traversal ofBinary Tree Traversal Methods In a traversal of
Binary Tree Traversal Methods In a traversal ofBinary Tree Traversal Methods In a traversal of
In Order Traversal Algorithm In Order traversal algorithmIn Order Traversal Algorithm In Order traversal algorithm
Algoritma Traversal Graph Graph Traversal Algorithms In generalAlgoritma Traversal Graph Graph Traversal Algorithms In general
Inorder Traversal Inorder traversal Visit the left subtreeInorder Traversal Inorder traversal Visit the left subtree
Binary Tree Traversal Traversal of Binary Tree nBinary Tree Traversal Traversal of Binary Tree n
Tree Traversal Techniques Heaps Tree Traversal Concept TreeTree Traversal Techniques Heaps Tree Traversal Concept Tree
Lattice Oil Bond function price lattice Lattice OilLattice Oil Bond function price lattice Lattice Oil