RECIPROCAL LATTICE a b 0 1 REAL LATTICE

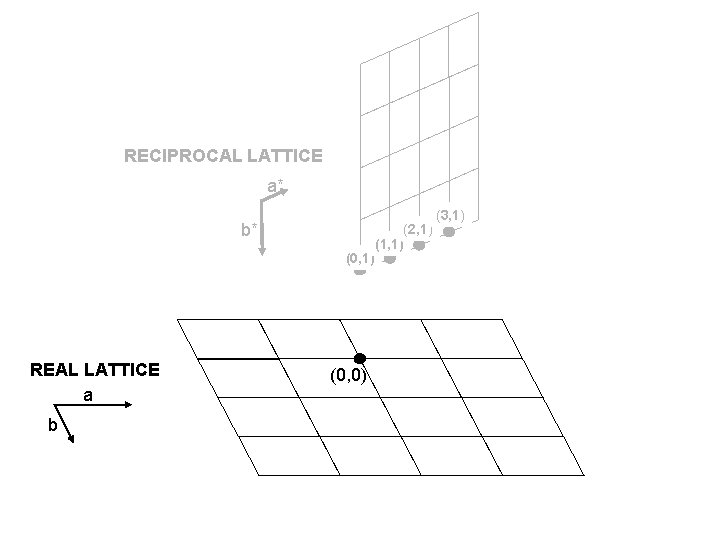
RECIPROCAL LATTICE a* b* (0, 1) REAL LATTICE a b (0, 0) (2, 1) (1, 1) (3, 1)

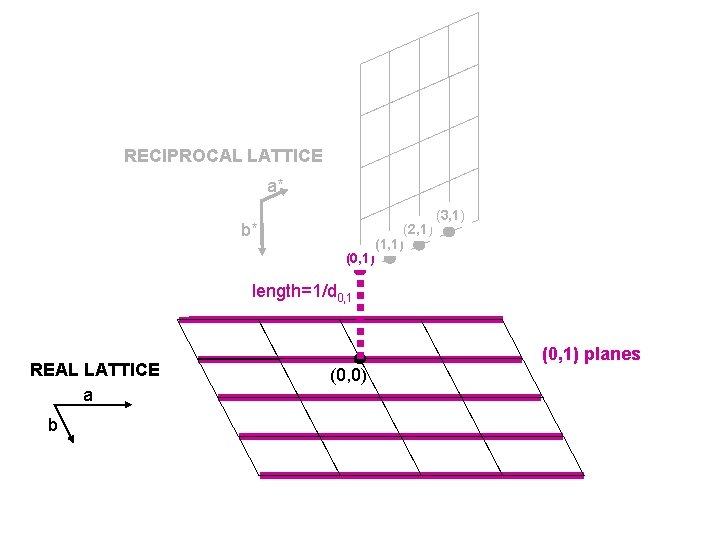
RECIPROCAL LATTICE a* b* (0, 1) (2, 1) (1, 1) (3, 1) length=1/d 0, 1 REAL LATTICE a b (0, 1) planes (0, 0)

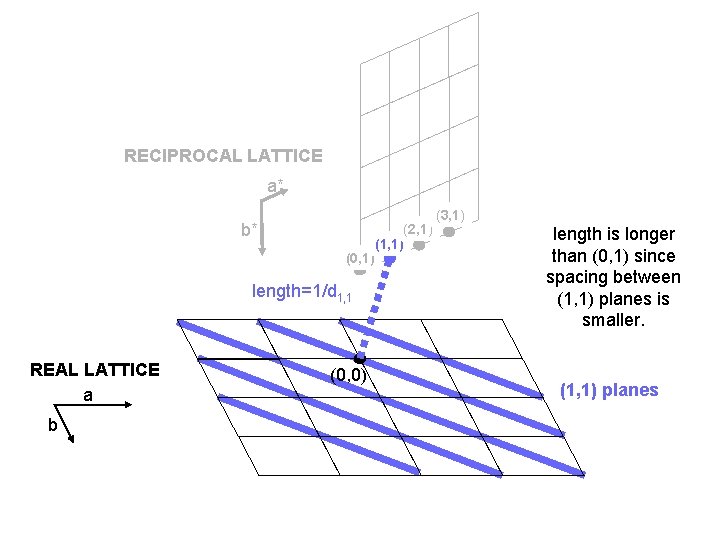
RECIPROCAL LATTICE a* b* (0, 1) length=1/d 1, 1 REAL LATTICE a b (0, 0) (2, 1) (1, 1) (3, 1) length is longer than (0, 1) since spacing between (1, 1) planes is smaller. (1, 1) planes

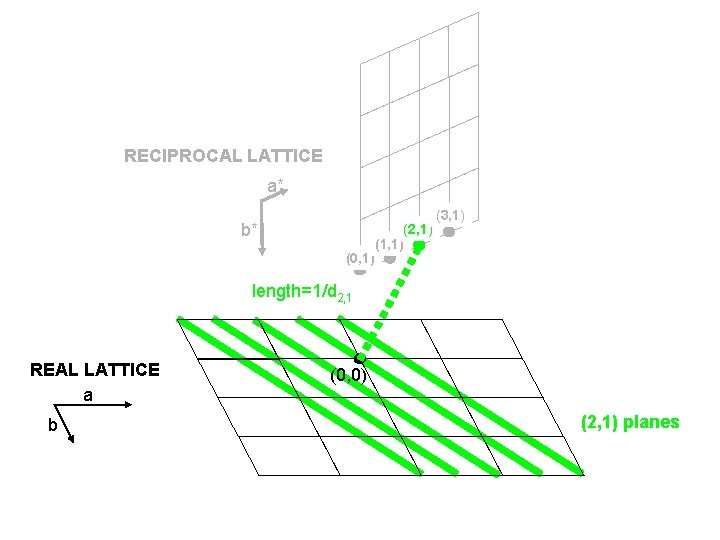
RECIPROCAL LATTICE a* b* (0, 1) (2, 1) (1, 1) (3, 1) length=1/d 2, 1 REAL LATTICE a b (0, 0) (2, 1) planes

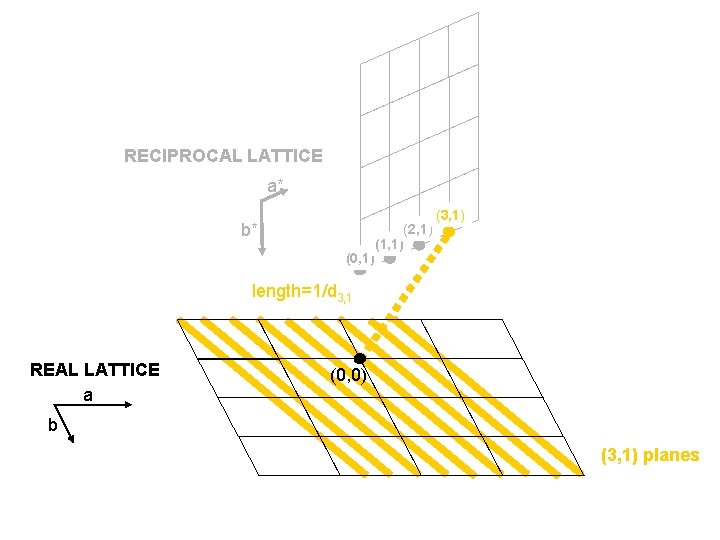
RECIPROCAL LATTICE a* b* (0, 1) (2, 1) (1, 1) (3, 1) length=1/d 3, 1 REAL LATTICE a (0, 0) b (3, 1) planes

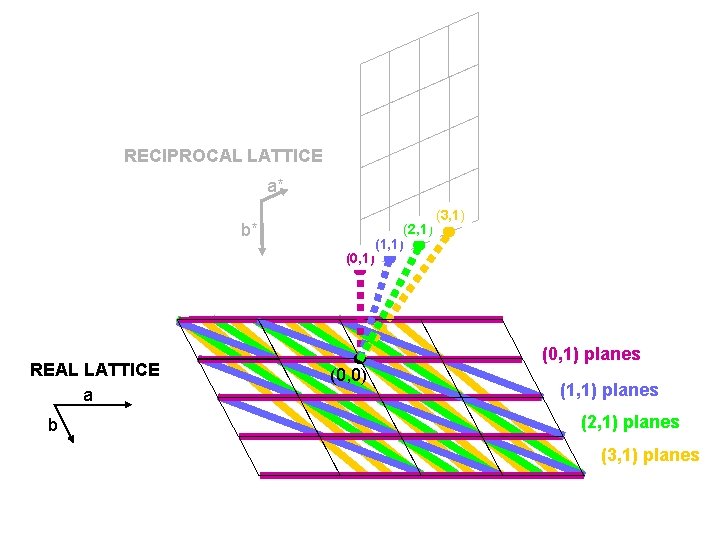
RECIPROCAL LATTICE a* b* (0, 1) REAL LATTICE a b (2, 1) (1, 1) (3, 1) (0, 1) planes (0, 0) (1, 1) planes (2, 1) planes (3, 1) planes

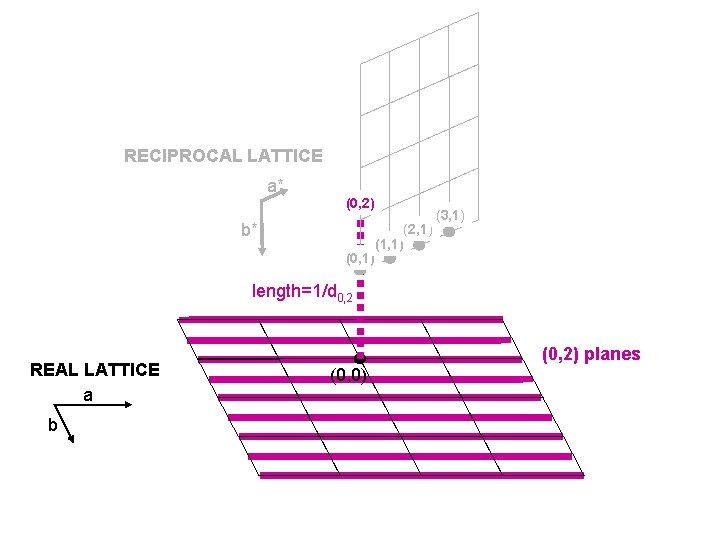
RECIPROCAL LATTICE a* (0, 2) b* (0, 1) (2, 1) (1, 1) (3, 1) length=1/d 0, 2 REAL LATTICE a b (0, 2) planes (0, 0)

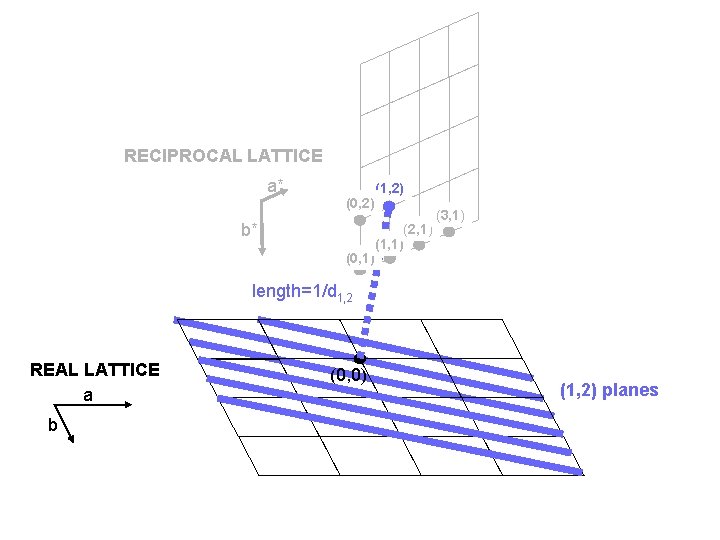
RECIPROCAL LATTICE a* (0, 2) b* (0, 1) (1, 2) (2, 1) (1, 1) (3, 1) length=1/d 1, 2 REAL LATTICE a b (0, 0) (1, 2) planes

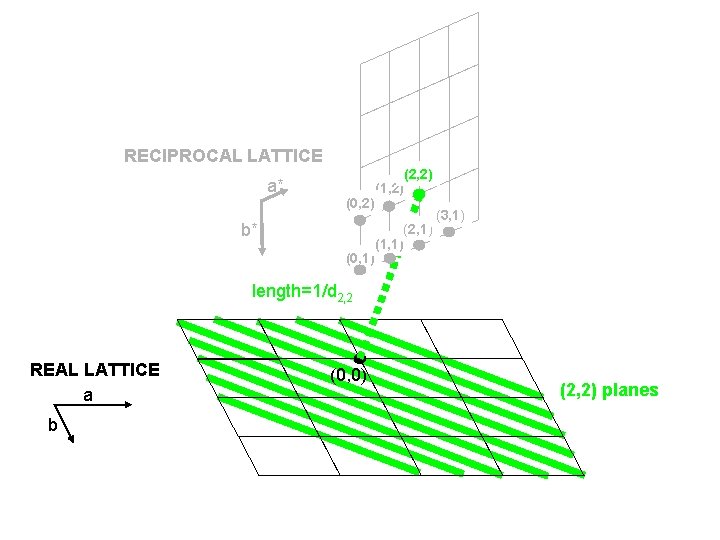
RECIPROCAL LATTICE a* (0, 2) b* (0, 1) (2, 2) (1, 2) (2, 1) (1, 1) (3, 1) length=1/d 2, 2 REAL LATTICE a b (0, 0) (2, 2) planes

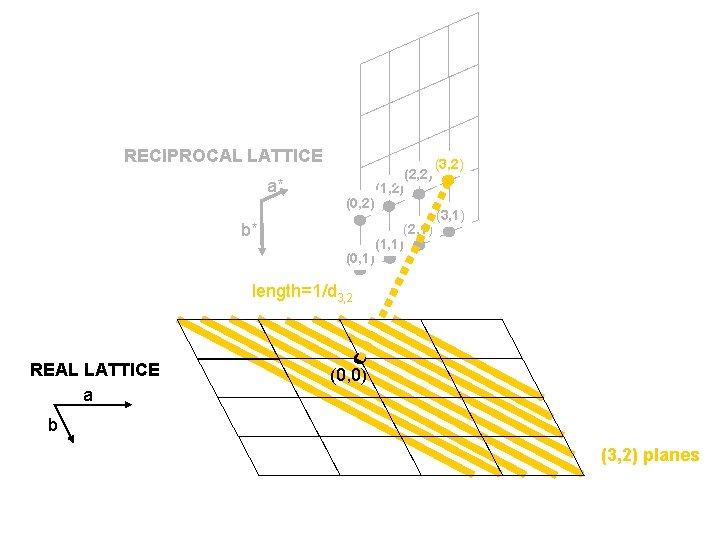
RECIPROCAL LATTICE a* (0, 2) b* (0, 1) (2, 2) (1, 2) (2, 1) (1, 1) (3, 2) (3, 1) length=1/d 3, 2 REAL LATTICE a (0, 0) b (3, 2) planes

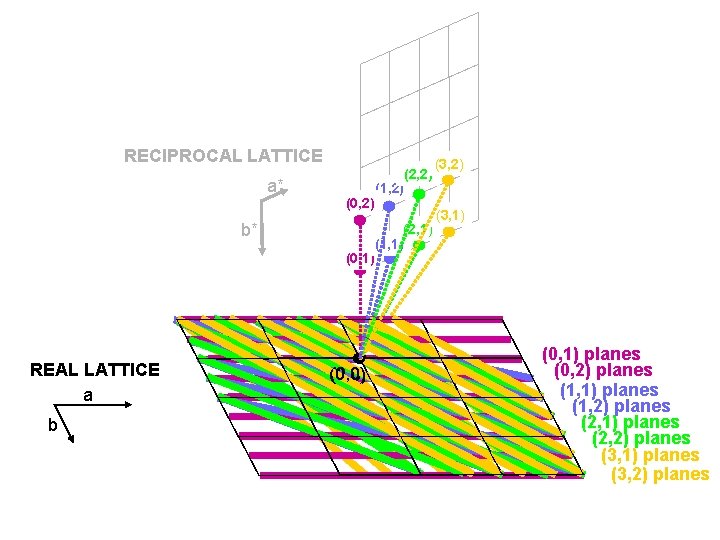
RECIPROCAL LATTICE a* (0, 2) b* (0, 1) REAL LATTICE a b (0, 0) (2, 2) (1, 2) (2, 1) (1, 1) (3, 2) (3, 1) (0, 1) planes (0, 2) planes (1, 1) planes (1, 2) planes (2, 1) planes (2, 2) planes (3, 1) planes (3, 2) planes

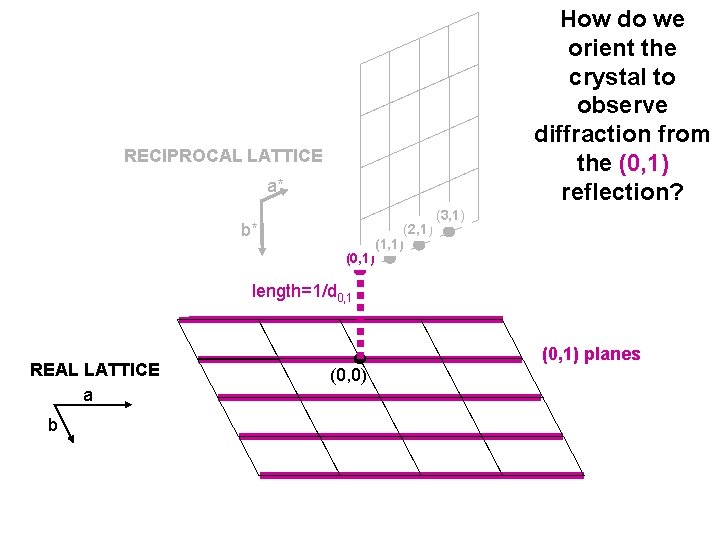
How do we orient the crystal to observe diffraction from the (0, 1) reflection? RECIPROCAL LATTICE a* b* (0, 1) (2, 1) (1, 1) (3, 1) length=1/d 0, 1 REAL LATTICE a b (0, 1) planes (0, 0)

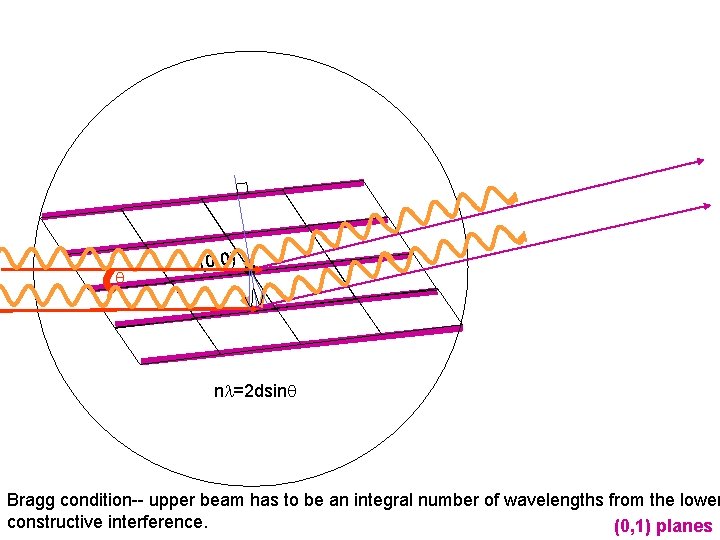
q (0, 0) nl=2 dsinq Bragg condition-- upper beam has to be an integral number of wavelengths from the lower constructive interference. (0, 1) planes

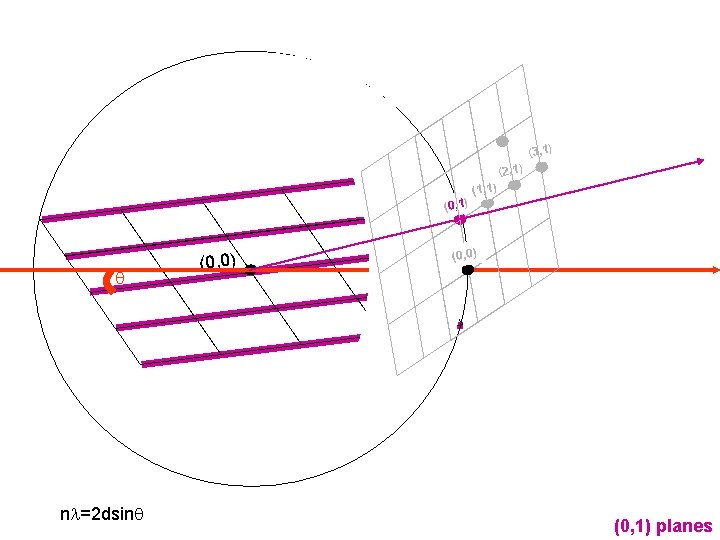
(3, 1) (2, 1) (0, 1) q nl=2 dsinq (0, 0) (1, 1) (0, 0) (0, 1) planes

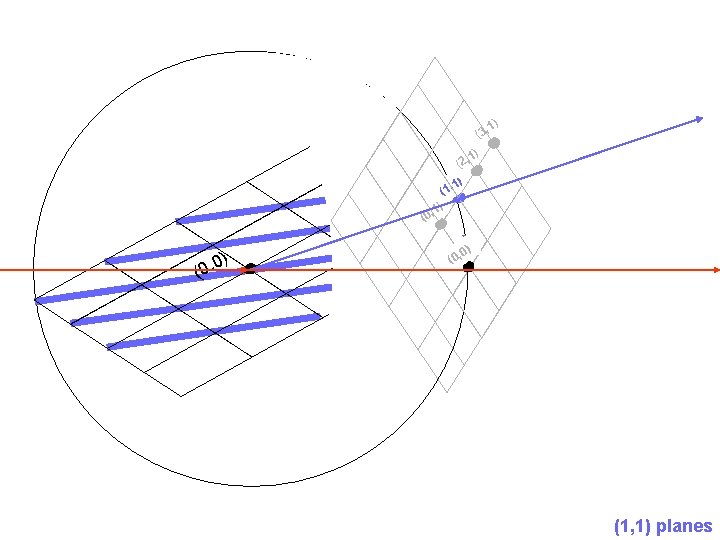
(3, (0 (0 , 0) (1 , 1) (2, , 1) 1) 1) ) 0 (0, (1, 1) planes

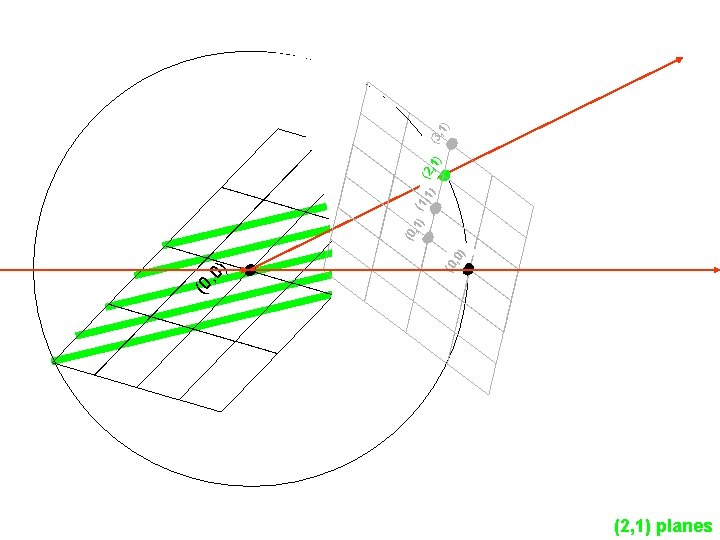
(2, 1) planes ) (0 , 0 ) , 0 (0 ) (1, 1) (2, 1) , 1 (0 (3 , 1)