Lattice modulation experiments with fermions in optical lattice

Lattice modulation experiments with fermions in optical lattice Dynamics of Hubbard model Ehud Altman David Pekker Rajdeep Sensarma Eugene Demler Weizmann Institute Harvard University Thanks to I. Bloch, T. Esslinger, M. Lukin, A. M. Rey

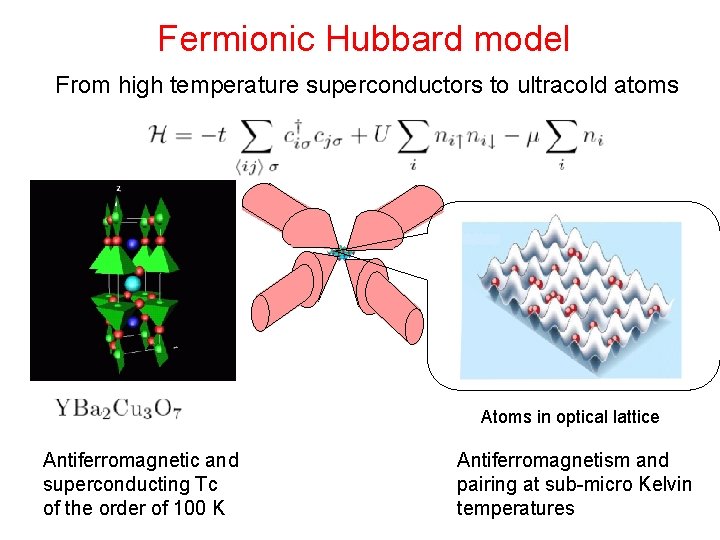
Fermionic Hubbard model From high temperature superconductors to ultracold atoms Atoms in optical lattice Antiferromagnetic and superconducting Tc of the order of 100 K Antiferromagnetism and pairing at sub-micro Kelvin temperatures

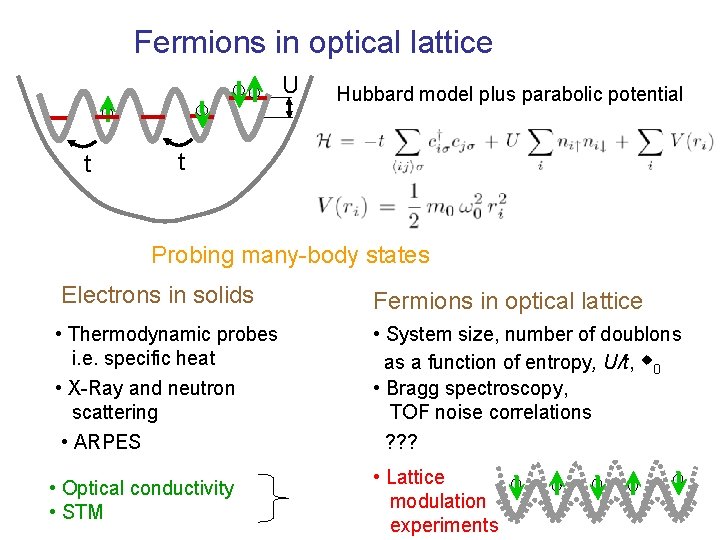
Fermions in optical lattice U t Hubbard model plus parabolic potential t Probing many-body states Electrons in solids Fermions in optical lattice • Thermodynamic probes i. e. specific heat • X-Ray and neutron scattering • ARPES • System size, number of doublons as a function of entropy, U/t, w 0 • Bragg spectroscopy, TOF noise correlations ? ? ? • Optical conductivity • STM • Lattice modulation experiments

Outline • Introduction. Recent experiments with fermions in optical lattice Signatures of Mott state Observation of Superexchange • Lattice modulation experiments in the Mott state. Linear response theory • Comparison to experiments • Lattice modulation experiments with d-wave superfluids

Mott state of fermions in optical lattice

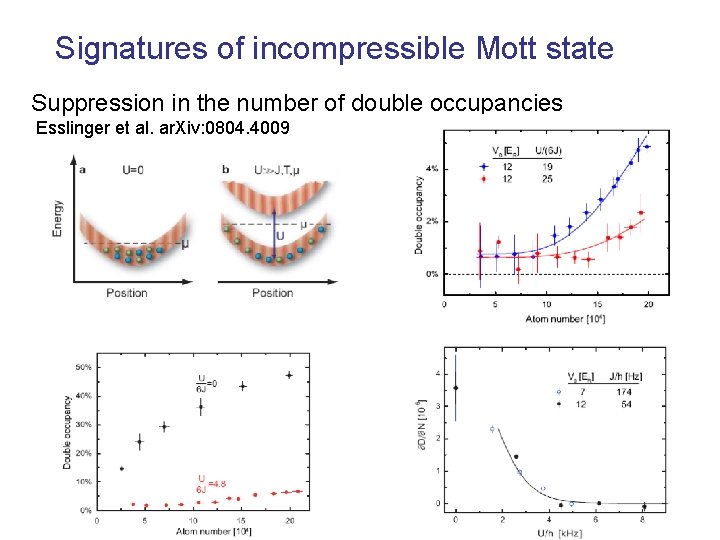
Signatures of incompressible Mott state Suppression in the number of double occupancies Esslinger et al. ar. Xiv: 0804. 4009

Signatures of incompressible Mott state Response to external potential I. Bloch et al. , unpublished Radius of the cloud as a function of the confining potential Comparison with DMFT+LDA models suggests that temperature is above the Neel transition Next step: observation of antiferromagnetic order However superexchange interactions have already been observed

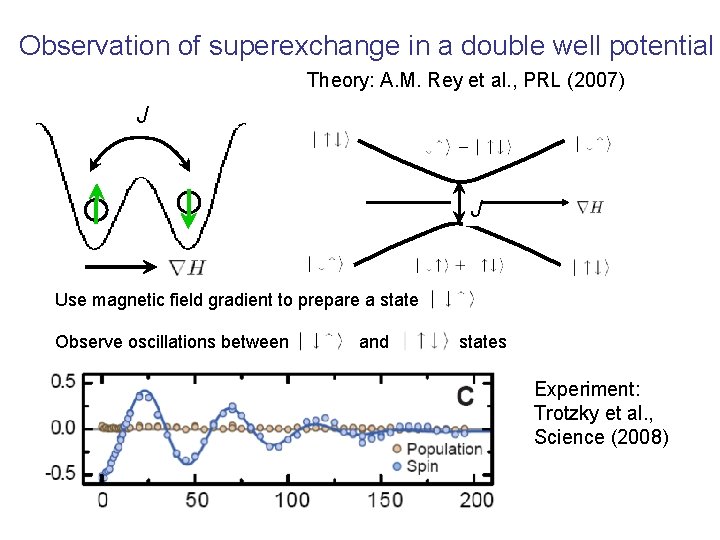
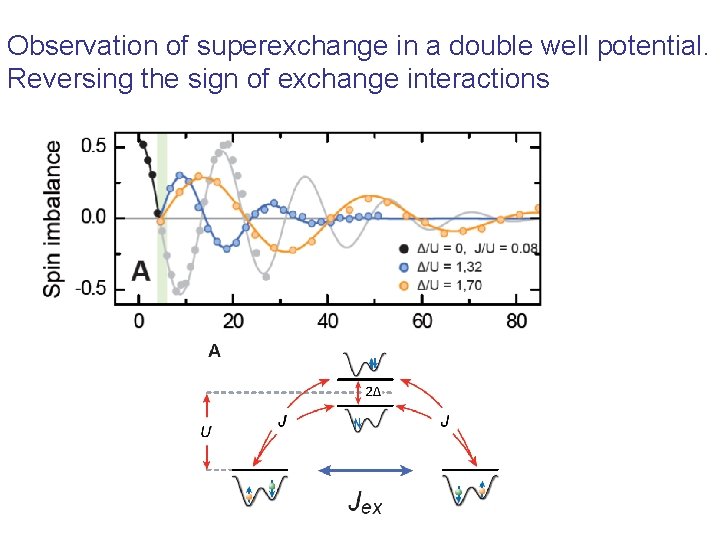
Superexchange interaction in experiments with double wells Refs: Theory: A. M. Rey et al. , Phys. Rev. Lett. 99: 140601 (2007) Experiment: S. Trotzky et al. , Science 319: 295 (2008)

Two component Bose mixture in optical lattice Example: . Mandel et al. , Nature 425: 937 (2003) t t Two component Bose Hubbard model

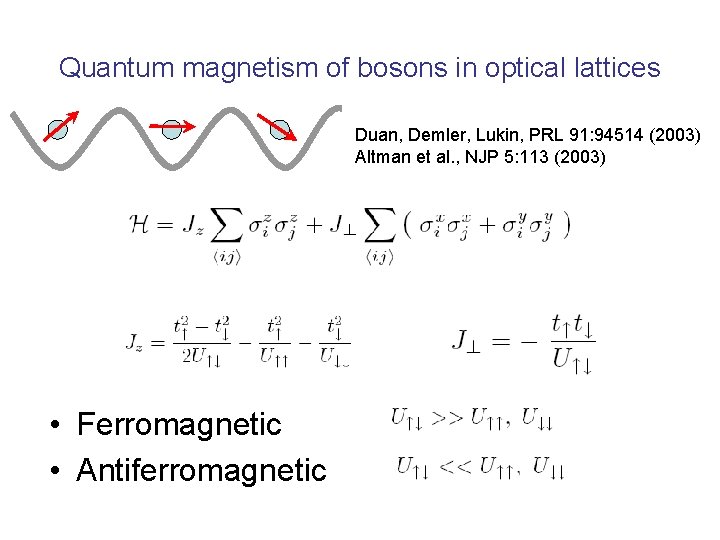
Quantum magnetism of bosons in optical lattices Duan, Demler, Lukin, PRL 91: 94514 (2003) Altman et al. , NJP 5: 113 (2003) • Ferromagnetic • Antiferromagnetic

Observation of superexchange in a double well potential Theory: A. M. Rey et al. , PRL (2007) J J Use magnetic field gradient to prepare a state Observe oscillations between and states Experiment: Trotzky et al. , Science (2008)

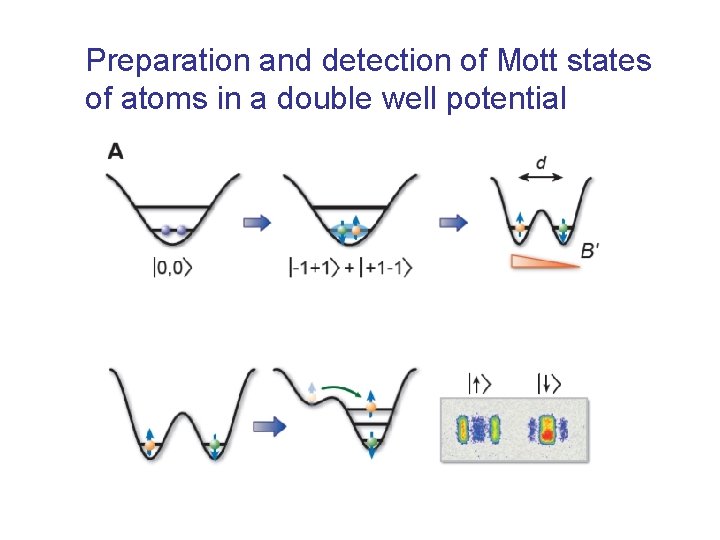
Preparation and detection of Mott states of atoms in a double well potential

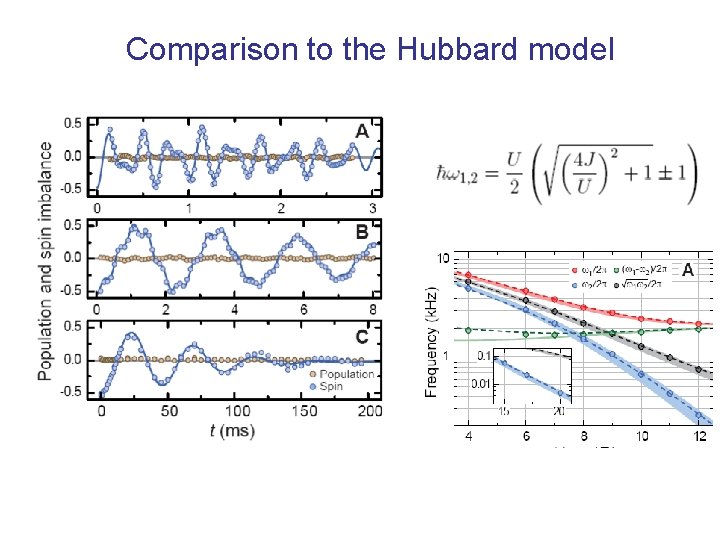
Comparison to the Hubbard model

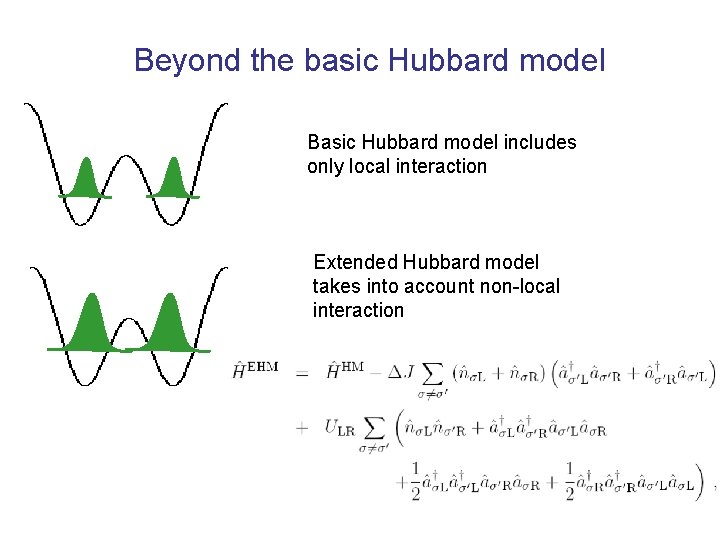
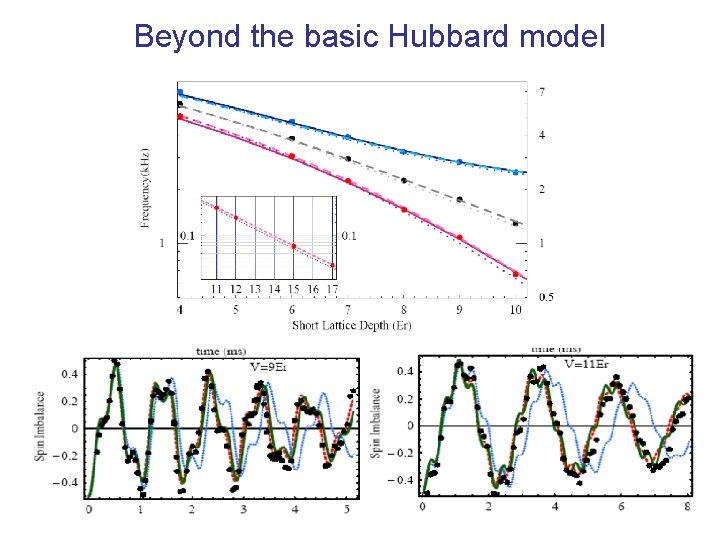
Beyond the basic Hubbard model Basic Hubbard model includes only local interaction Extended Hubbard model takes into account non-local interaction

Beyond the basic Hubbard model

Observation of superexchange in a double well potential. Reversing the sign of exchange interactions

Lattice modulation experiments with fermions in optical lattice. Mott state

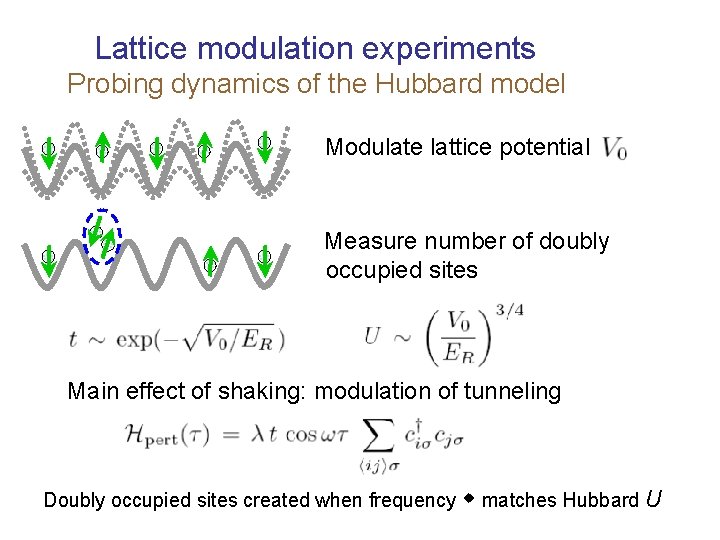
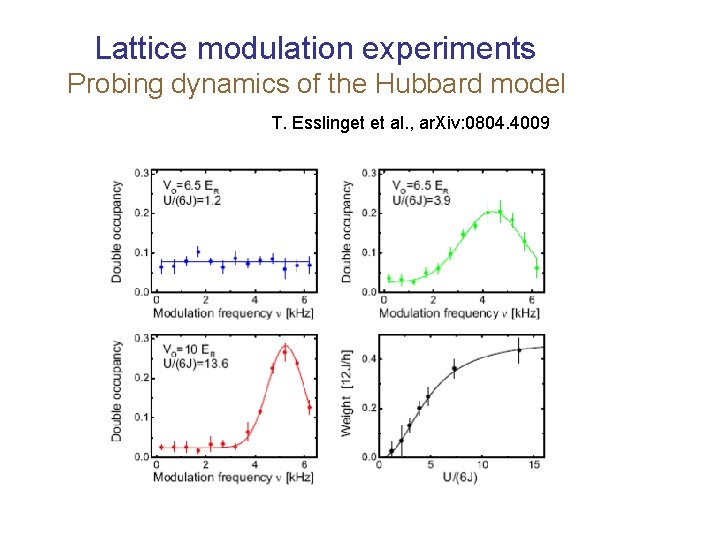
Lattice modulation experiments Probing dynamics of the Hubbard model Modulate lattice potential Measure number of doubly occupied sites Main effect of shaking: modulation of tunneling Doubly occupied sites created when frequency w matches Hubbard U

Lattice modulation experiments Probing dynamics of the Hubbard model T. Esslinget et al. , ar. Xiv: 0804. 4009

Mott state Regime of strong interactions U>>t. Mott gap for the charge forms at Antiferromagnetic ordering at “High” temperature regime All spin configurations are equally likely. Can neglect spin dynamics. “Low” temperature regime Spins are antiferromagnetically ordered or have strong correlations

Schwinger bosons and slave fermions Fermion hopping Propagation of holes and doublons is coupled to spin excitations. Neglect spontaneous doublon production and relaxation. Doublon production due to lattice modulation perturbation Second order perturbation theory. Number of doublons

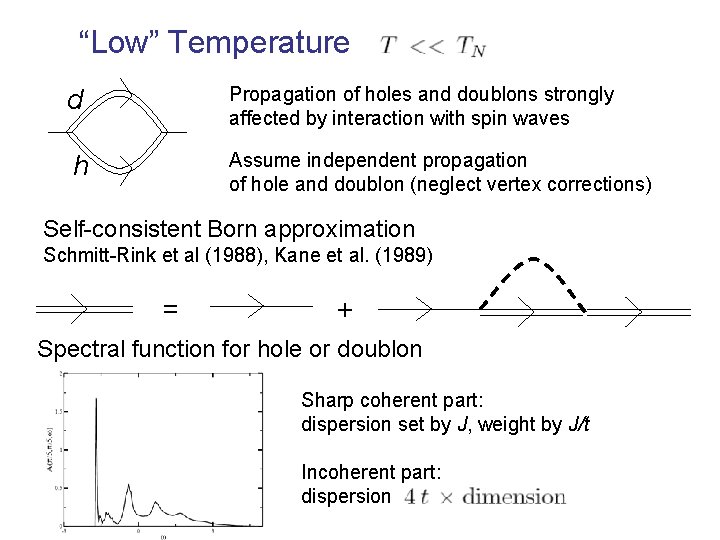
“Low” Temperature d Propagation of holes and doublons strongly affected by interaction with spin waves h Assume independent propagation of hole and doublon (neglect vertex corrections) Self-consistent Born approximation Schmitt-Rink et al (1988), Kane et al. (1989) = + Spectral function for hole or doublon Sharp coherent part: dispersion set by J, weight by J/t Incoherent part: dispersion

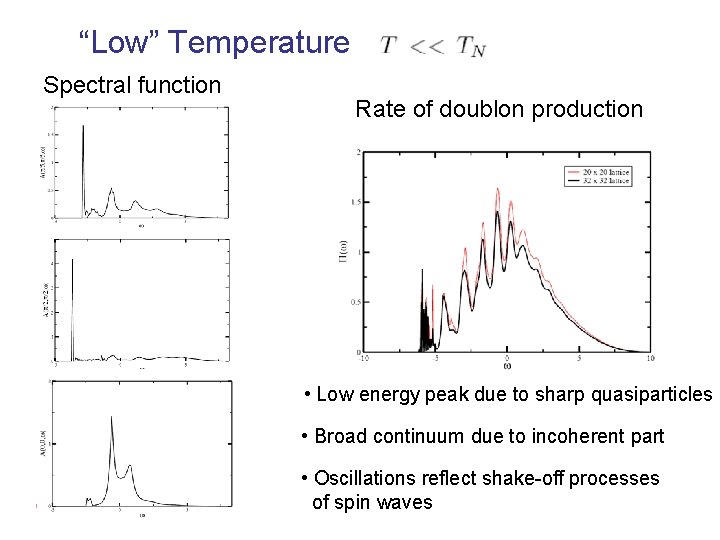
“Low” Temperature Spectral function Rate of doublon production • Low energy peak due to sharp quasiparticles • Broad continuum due to incoherent part • Oscillations reflect shake-off processes of spin waves

“High” Temperature Atomic limit. Neglect spin dynamics. All spin configurations are equally likely. Aij (t’) replaced by probability of having a singlet Assume independent propagation of doublons and holes. Rate of doublon production Ad(h) is the spectral function of a single doublon (holon)

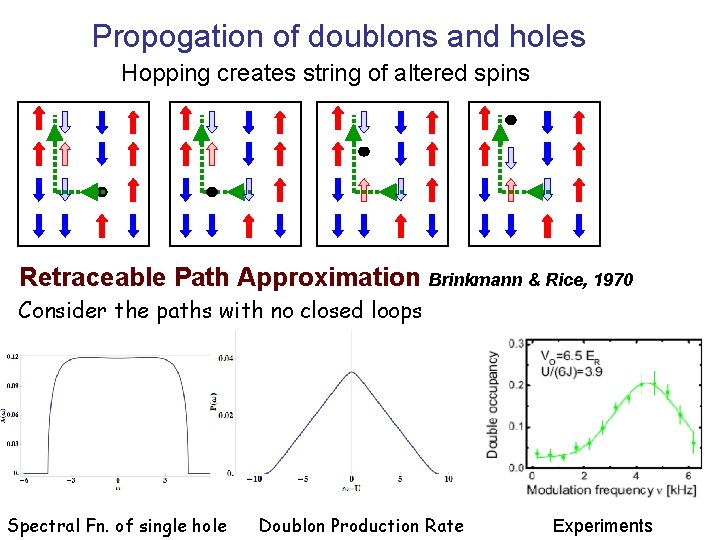
Propogation of doublons and holes Hopping creates string of altered spins Retraceable Path Approximation Brinkmann & Rice, 1970 Consider the paths with no closed loops Spectral Fn. of single hole Doublon Production Rate Experiments

Doublon decay and relaxation

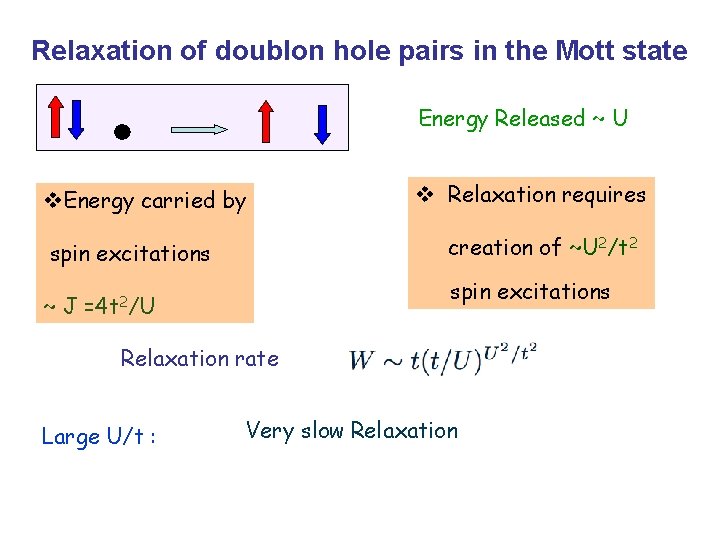
Relaxation of doublon hole pairs in the Mott state Energy Released ~ U v. Energy carried by creation of ~U 2/t 2 spin excitations ~J v Relaxation requires spin excitations =4 t 2/U Relaxation rate Large U/t : Very slow Relaxation

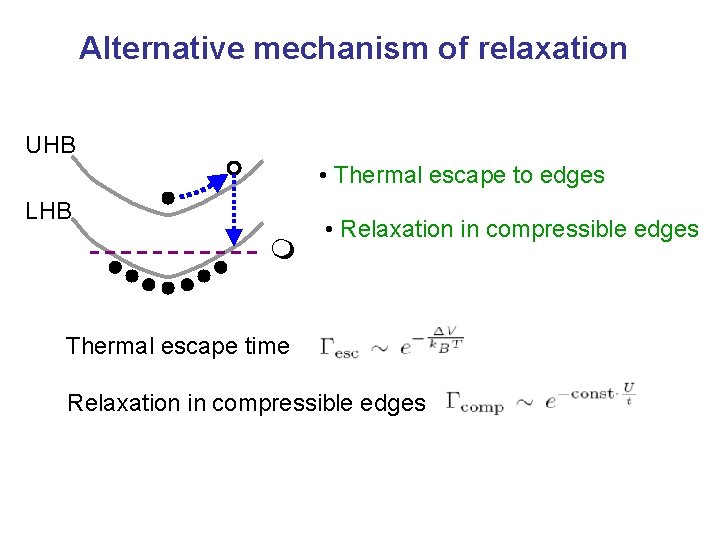
Alternative mechanism of relaxation UHB • Thermal escape to edges LHB m • Relaxation in compressible edges Thermal escape time Relaxation in compressible edges

Lattice modulation experiments with fermions in optical lattice. Detecting d-wave superfluid state

Setting: BCS superfluid • consider a mean-field description of the superfluid • s-wave: • d-wave: • anisotropic s-wave: Can we learn about paired states from lattice modulation experiments? Can we distinguish pairing symmetries?

Lattice modulation experiments Modulating hopping via modulation of the optical lattice intensity where • Equal energy contours Resonantly exciting quasiparticles with Enhancement close to the banana tips due to coherence factors

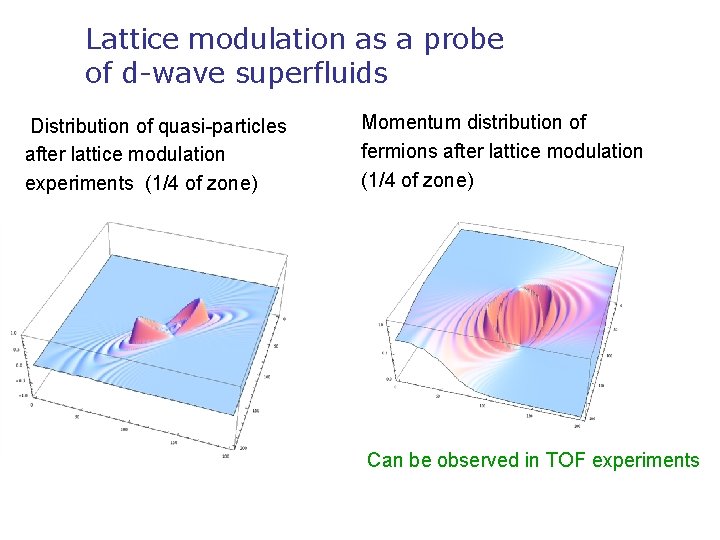
Lattice modulation as a probe of d-wave superfluids Distribution of quasi-particles after lattice modulation experiments (1/4 of zone) Momentum distribution of fermions after lattice modulation (1/4 of zone) Can be observed in TOF experiments

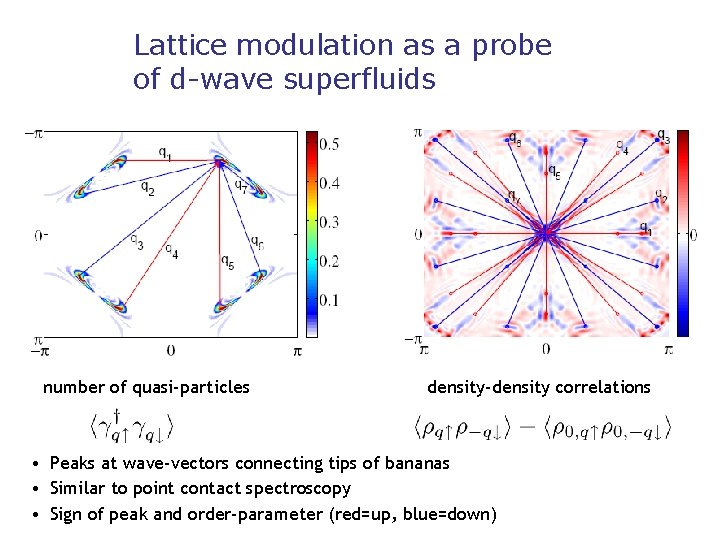
Lattice modulation as a probe of d-wave superfluids number of quasi-particles density-density correlations • Peaks at wave-vectors connecting tips of bananas • Similar to point contact spectroscopy • Sign of peak and order-parameter (red=up, blue=down)

Conclusions Experiments with fermions in optical lattice open many interesting questions about dynamics of the Hubbard model Thanks to: Harvard-MIT