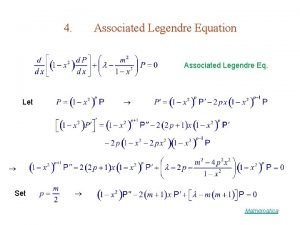TUTORIAL ON HARMONICS Theory and Computation Techniques C














![Effect of DC Offset New RMS= SQRT [ (RMS of Unshifted)2+(DC offset)2] Effect of DC Offset New RMS= SQRT [ (RMS of Unshifted)2+(DC offset)2]](https://slidetodoc.com/presentation_image_h/a23979d79ed9185baa72550146855913/image-26.jpg)




























- Slides: 96

TUTORIAL ON HARMONICS Theory and Computation Techniques C. J. Hatziadoniu: hatz@siu. edu

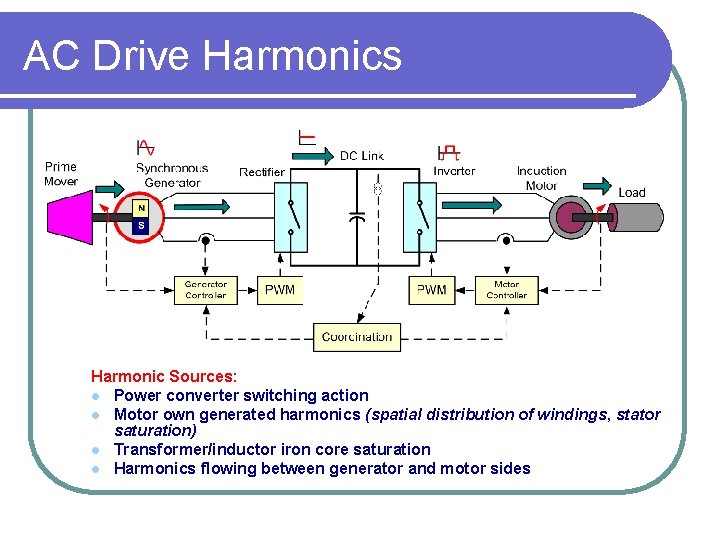
AC Drive Harmonics Harmonic Sources: l Power converter switching action l Motor own generated harmonics (spatial distribution of windings, stator saturation) l Transformer/inductor iron core saturation l Harmonics flowing between generator and motor sides

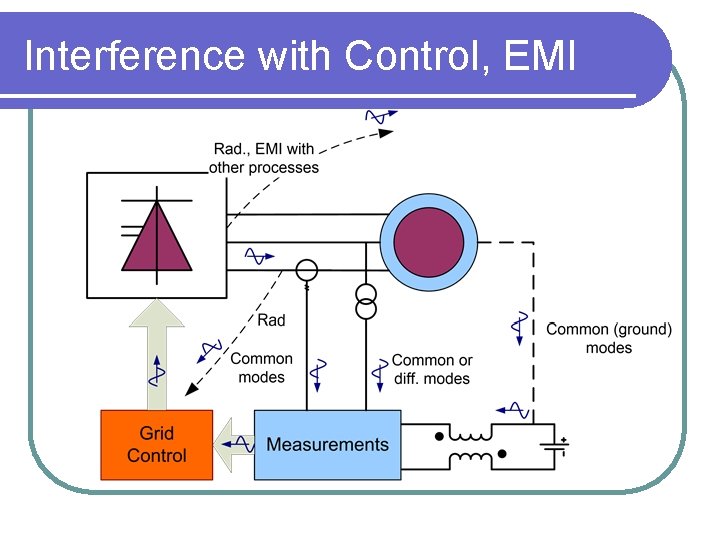
Potential Problems due to Harmonics l Power losses and heating: reduced efficiency, equipment de-rating l Over-voltage and voltage spiking, due to resonance: insulation stressing, limiting the forward and reverse blocking voltage of power semiconductor devices, heating, de-rating l EMI: noise, control inaccuracy or instability l Torque pulsation: mechanical fatigue, start-up limitation

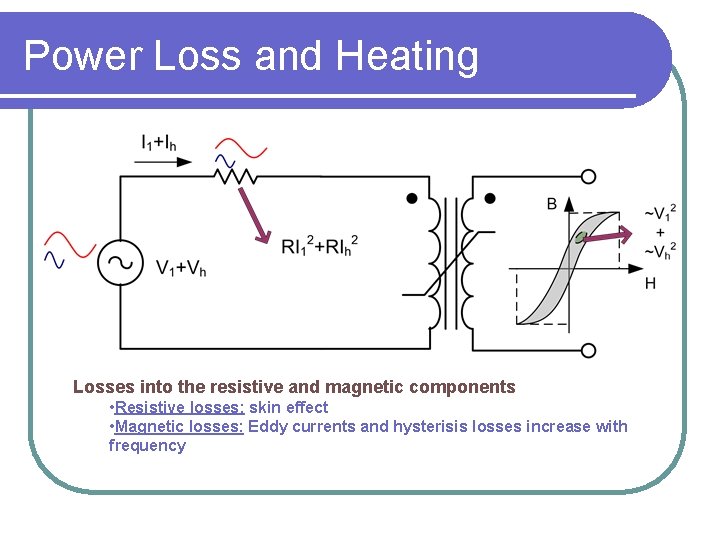
Power Loss and Heating Losses into the resistive and magnetic components • Resistive losses: skin effect • Magnetic losses: Eddy currents and hysterisis losses increase with frequency

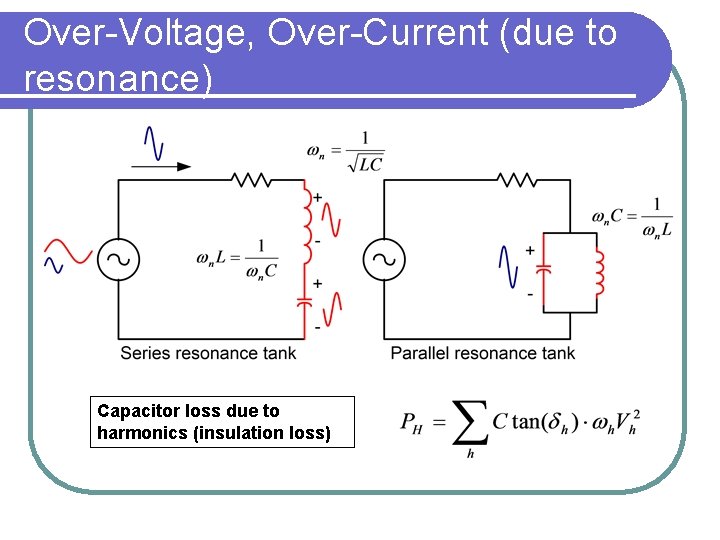
Over-Voltage, Over-Current (due to resonance) Capacitor loss due to harmonics (insulation loss)

Interference with Control, EMI

What Are Harmonics? l. Technical Description A high frequency sinusoidal current or voltage produced by certain nonlinear and switching processes in the system during normal periodic operation (steady state); l l The harmonic frequency is an integer multiple of the system operating frequency (fundamental). The non-sinusoidal part in a periodic voltage or current is the harmonic ripple or harmonic distortion—comprised of harmonic frequencies. l. Mathematical Definition l Sine and cosine functions of time with frequencies that are integer multiples of a fundamental frequency l Harmonic sine and cosine functions sum up to a periodic (nonsinusoidal) function l Terms of the Fourier series expansion of a periodic function;

Harmonic Analysis l What is it? l Principles, properties and methods for expressing periodic functions as sum of (harmonic) sine and cosine terms: l l Fourier Series Fourier Transform Discrete Fourier Transform Where is it used? l Obtain the response of a system to arbitrary periodic inputs; quantify/assess harmonic effects at each frequency l Framework for describing the quality of the system input and output signals (spectrum)

Superposition l A LTI system responds linearly to its inputs l ui 1 uo 1, ui 2 uo 2 l l aui 1+bui 2 auo 1+buo 2 For sinusoidal inputs:

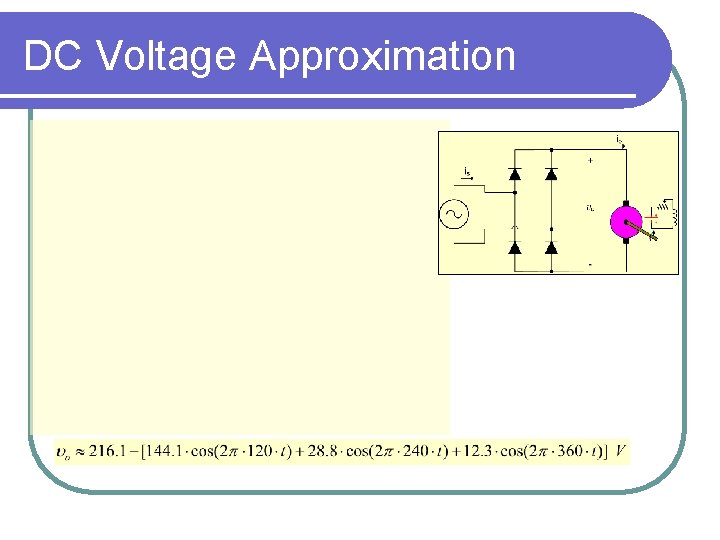
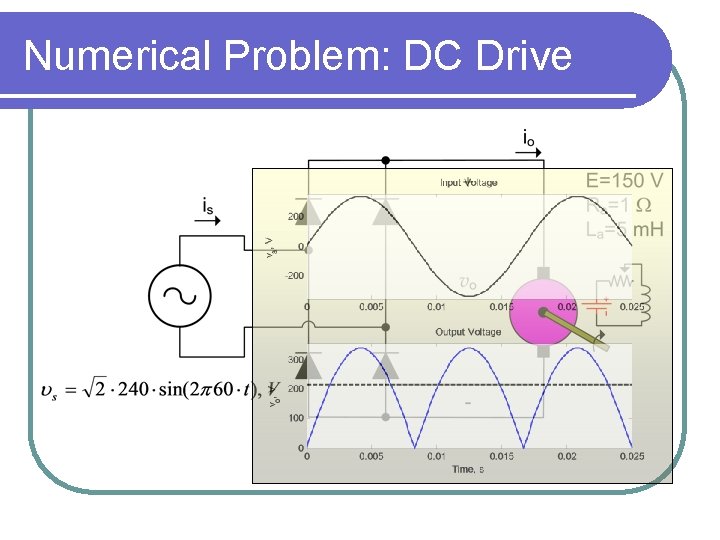
Application preview: DC Drive Find the armature current io(t) below

DC Voltage Approximation

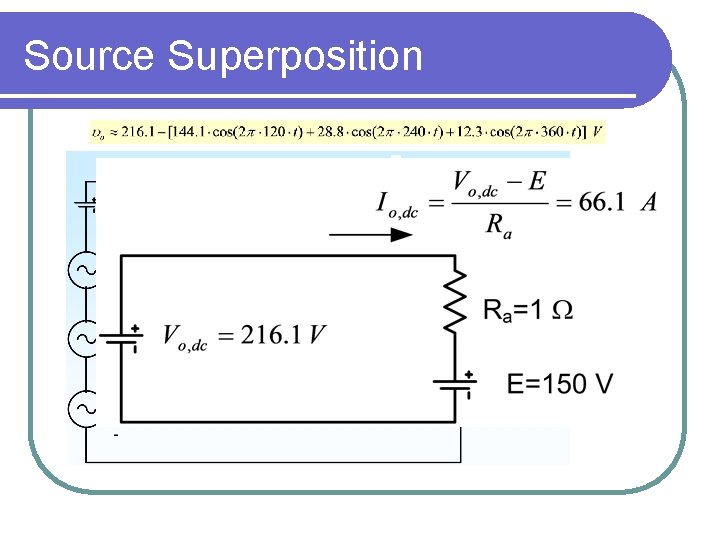
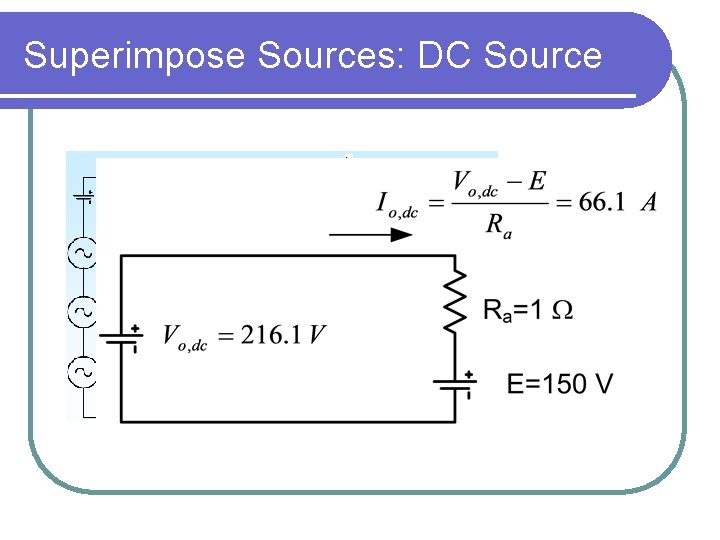
Source Superposition

Output Response

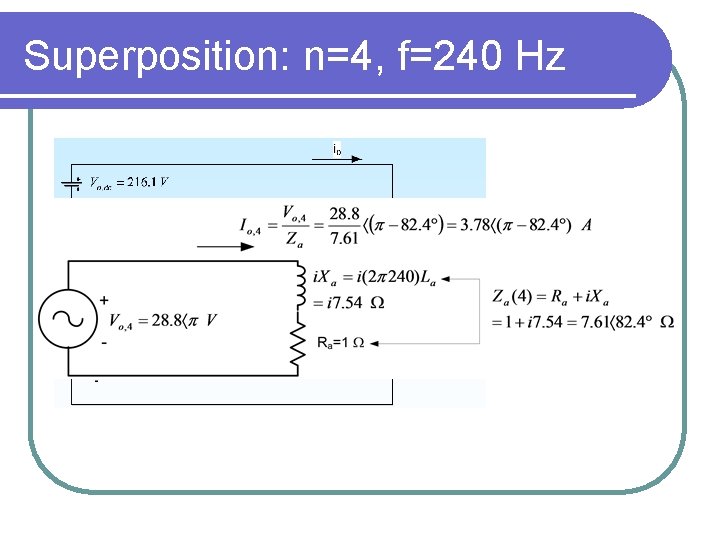
Procedure to obtain response Step 1: Obtain the harmonic composition of the input (Fourier Analysis) Step 2: Obtain the system output at each input frequency (equivalent circuit, T. F. frequency response) Step 3: Sum the outputs from Step 2.

Fundamental Theory Outline l Harmonic Fundamental Theory—Part a: Periodic Signals—sinusoidal function approximation l Fourier Series—definition, computation l Forms of the Fourier Series l Signal Spectrum l Applications of the FS in LTI l Wave Form Quality of Periodic Signals l

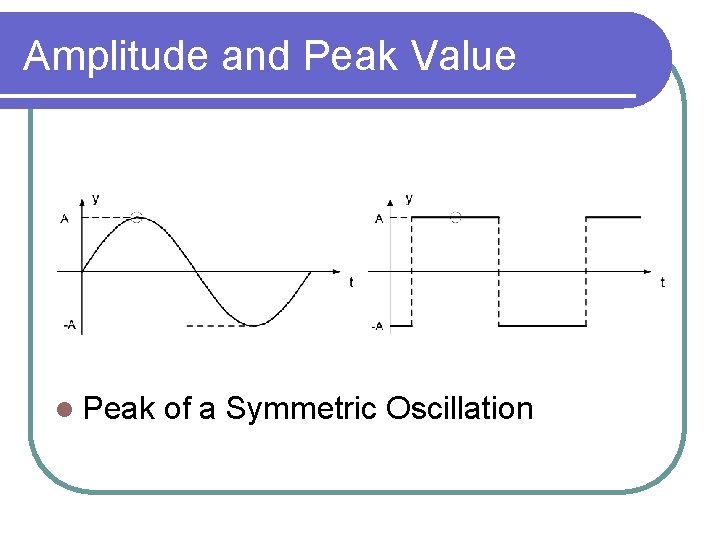
Measures Describing the Magnitude of a Signal l Amplitude l Average l Root and Peak Value or dc Offset Mean Square Value (RMS) or Power

Amplitude and Peak Value l Peak of a Symmetric Oscillation

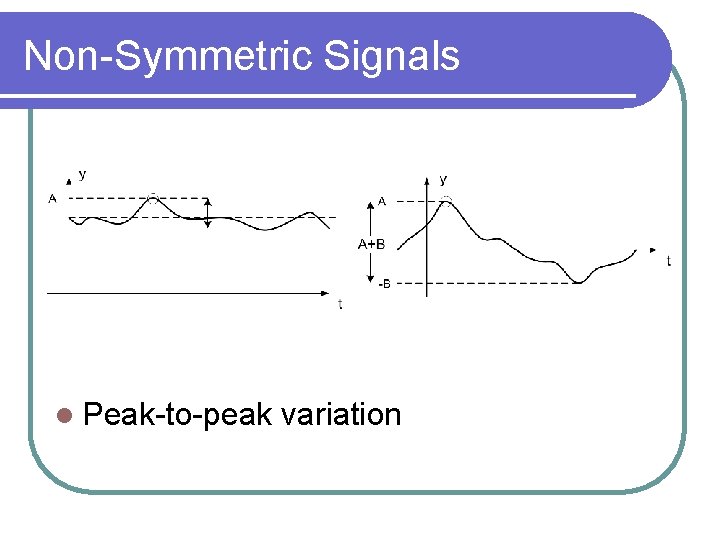
Non-Symmetric Signals l Peak-to-peak variation

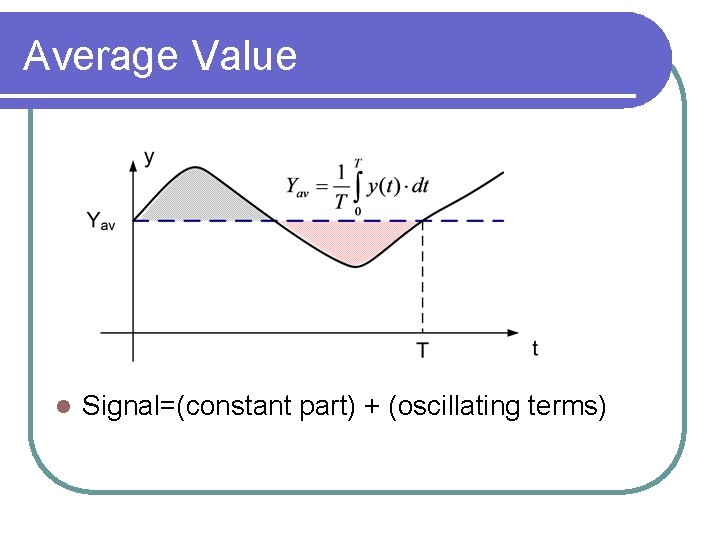
Average Value l Signal=(constant part) + (oscillating terms)

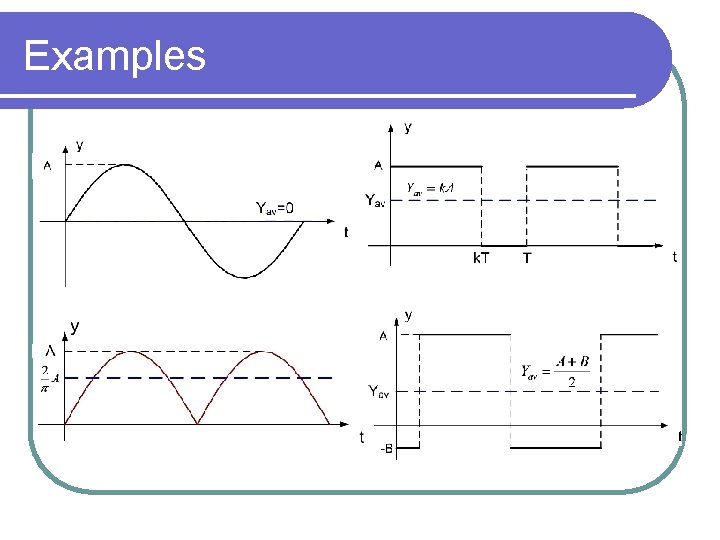
Examples

AC Signals l Zero Average Value

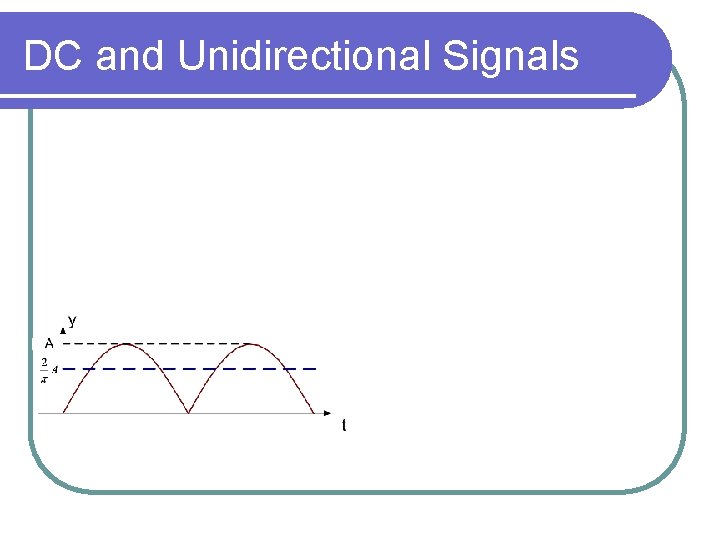
DC and Unidirectional Signals

Root Mean Square Value (RMS) For periodic signals, time window equals one period

Remarks on RMS l RMS is a measure of the overall magnitude of the signal (also referred to as norm or power of the signal). l The rms of current and voltage is directly related to power. l Electric equipment rating and size is given in voltage and current rms values.

Examples of Signal RMS
![Effect of DC Offset New RMS SQRT RMS of Unshifted2DC offset2 Effect of DC Offset New RMS= SQRT [ (RMS of Unshifted)2+(DC offset)2]](https://slidetodoc.com/presentation_image_h/a23979d79ed9185baa72550146855913/image-26.jpg)
Effect of DC Offset New RMS= SQRT [ (RMS of Unshifted)2+(DC offset)2]

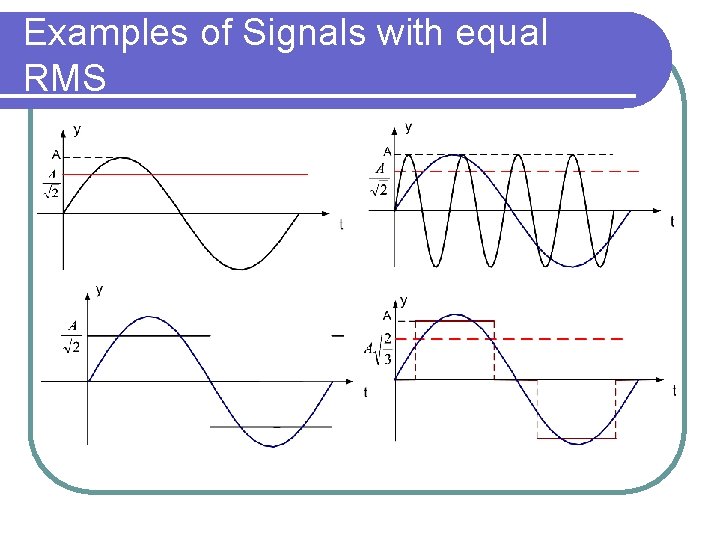
Examples of Signals with equal RMS

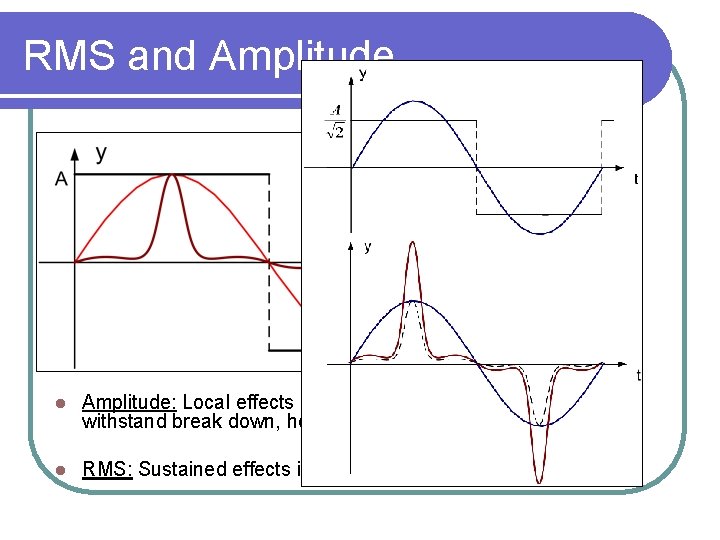
RMS and Amplitude l Amplitude: Local effects in time; Device insulation, voltage withstand break down, hot spots l RMS: Sustained effects in time; Heat dissipation, power output

Harmonic Analysis: Problem Statement l Approximate the square pulse function by a sinusoidal function in the interval [–T/2 , T/2]

General Problem l Find a cosine function of period T that best fits a given function f(t) in the interval [0, T] l Assumptions: f(t) is periodic of period T

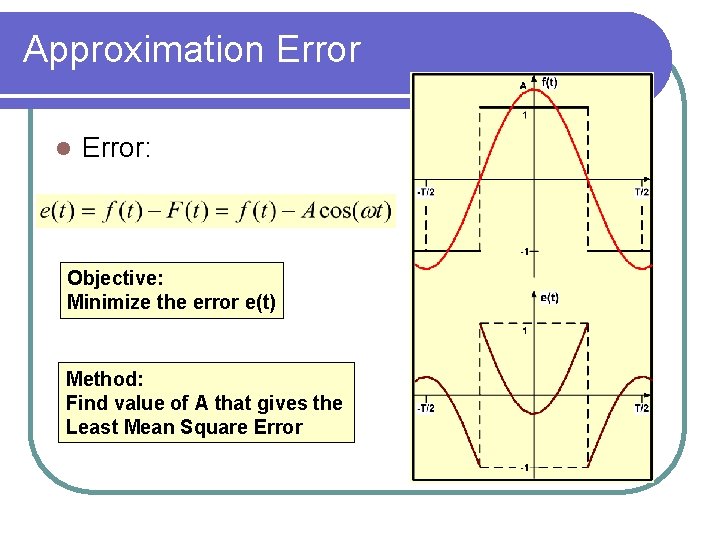
Approximation Error l Error: Objective: Minimize the error e(t) Method: Find value of A that gives the Least Mean Square Error

Procedure Define the average square error as : E is a quadratic function of A. The optimum choice of A is the one minimizing E.

Optimum Value of A Find d. E/d. A: Set d. E/d. A equal to zero

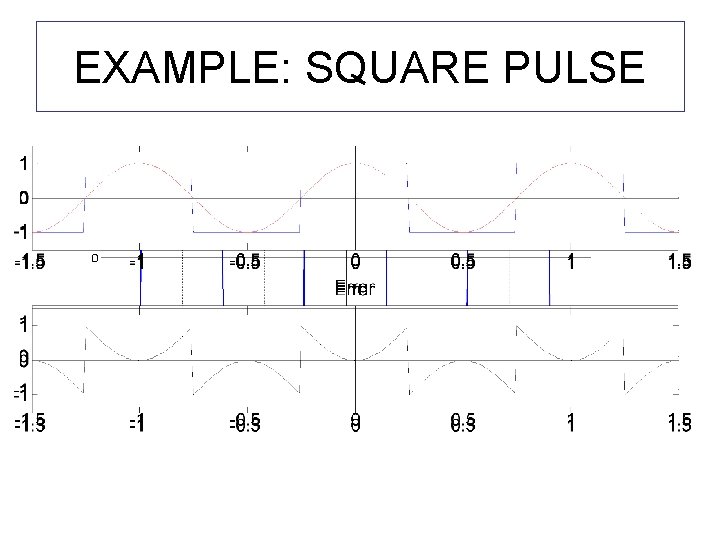
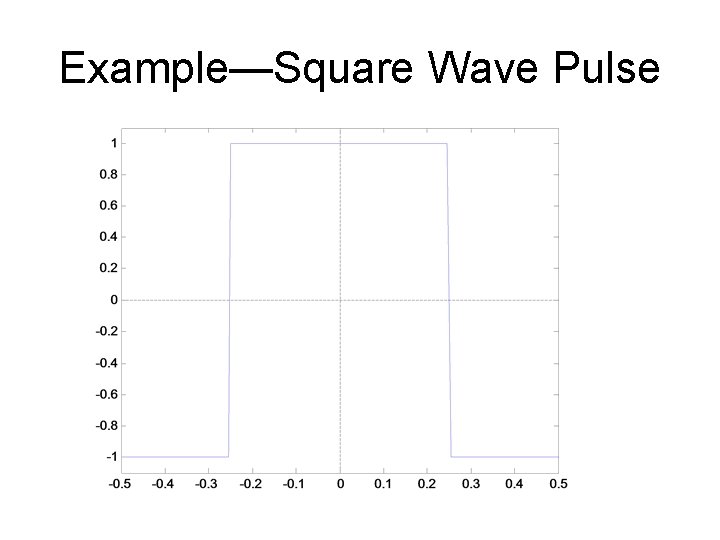
EXAMPLE: SQUARE PULSE

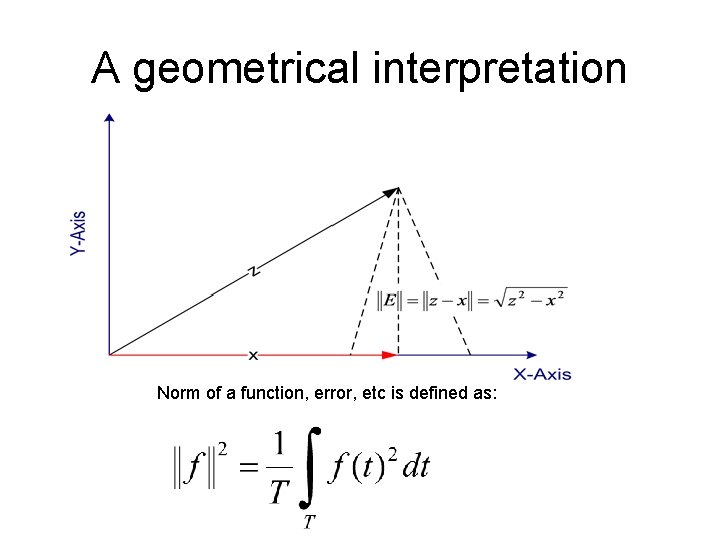
A geometrical interpretation Norm of a function, error, etc is defined as:

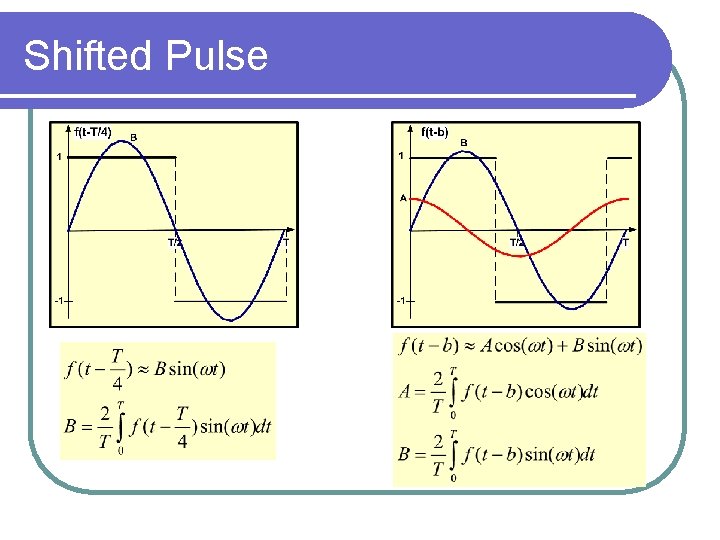
Shifted Pulse

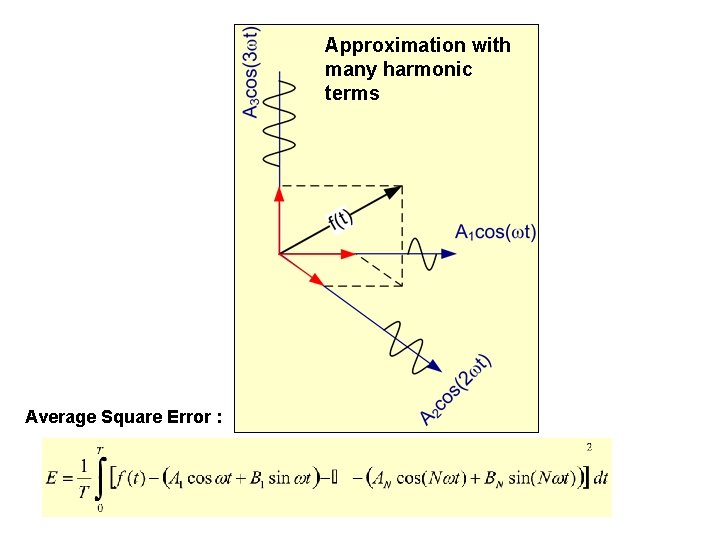
Approximation with many harmonic terms Average Square Error :

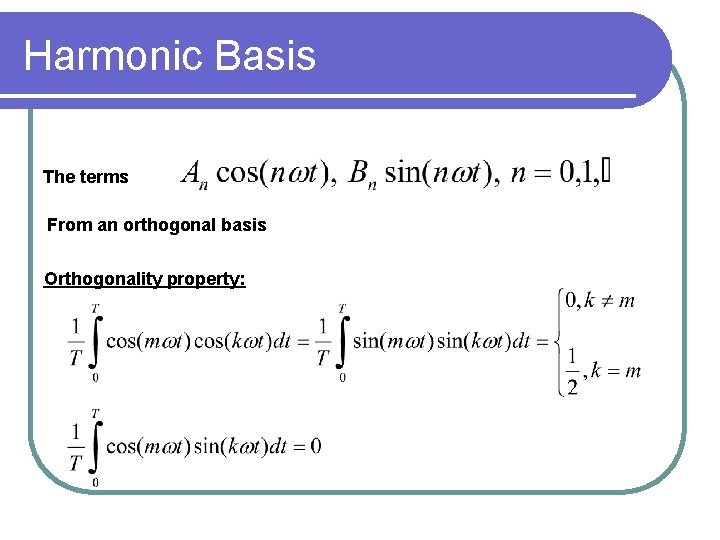
Harmonic Basis The terms From an orthogonal basis Orthogonality property:

Optimum coefficients l The property of orthogonality eliminates the cross harmonic product terms from the Sq. error l For each n, set

Optimum coefficients l Obtain the optimum expansion coefficients:

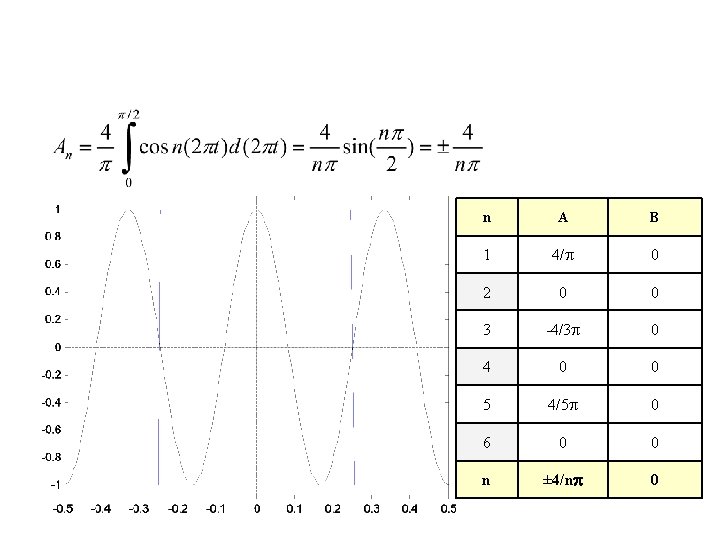
Example—Square Wave Pulse





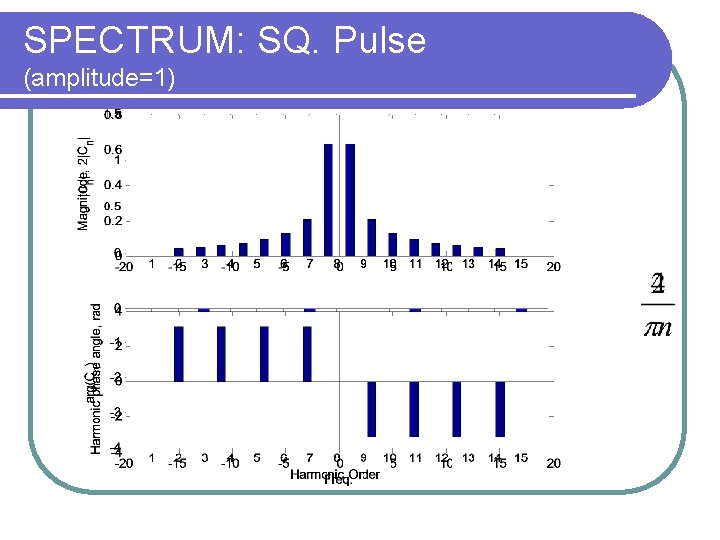
n A B 1 4/p 0 2 0 0 3 -4/3 p 0 4 0 0 5 4/5 p 0 6 0 0 n ± 4/np 0

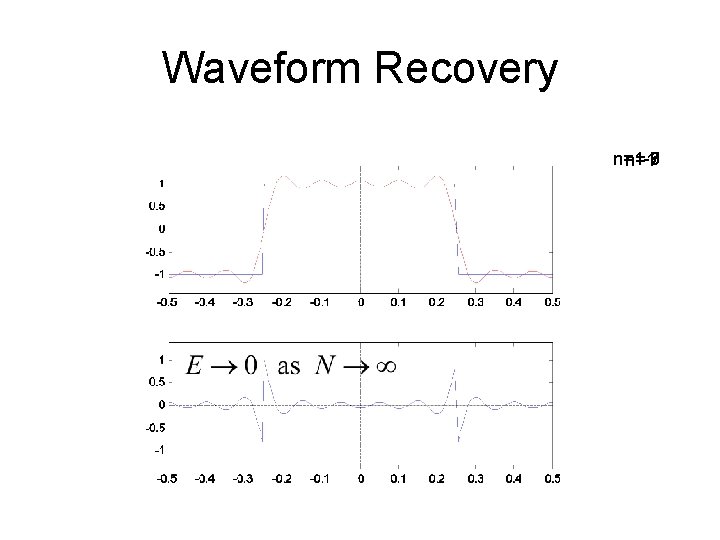
Waveform Recovery n=1 -3 n=1 -9 n=1 -7 n=1 -5 n=1

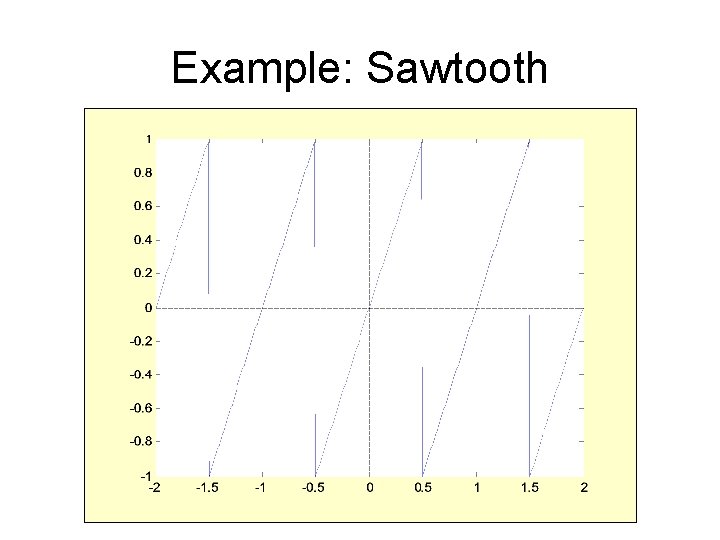
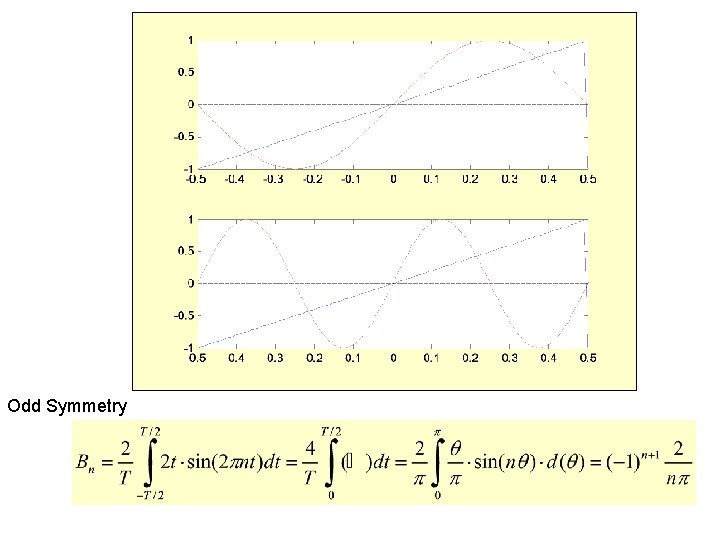
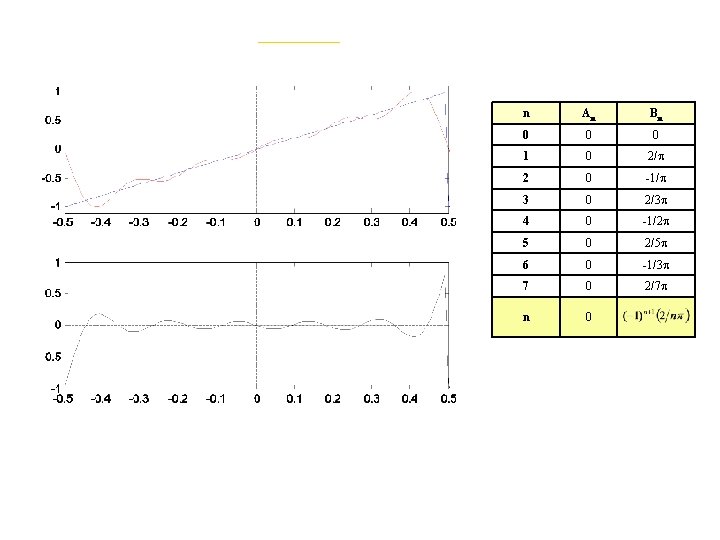
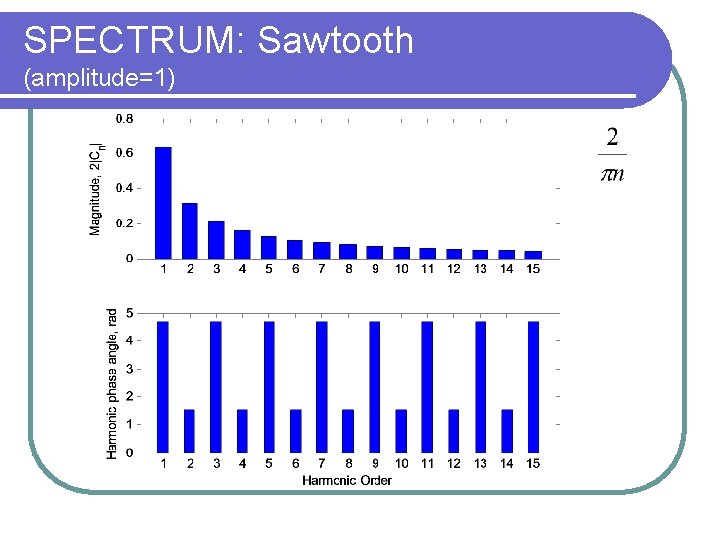
Example: Sawtooth

Odd Symmetry

n An Bn 0 0 0 1 0 2/p 2 0 -1/p 3 0 2/3 p 4 0 -1/2 p 5 0 2/5 p 6 0 -1/3 p 7 0 2/7 p n 0

Periodic Approximation

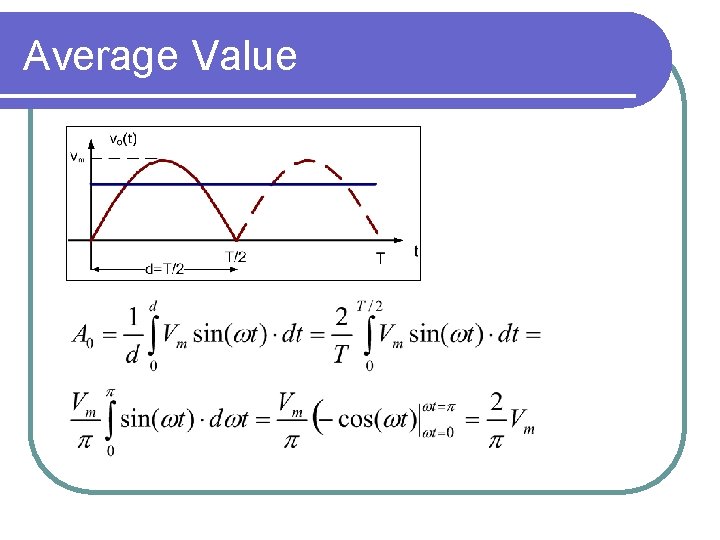
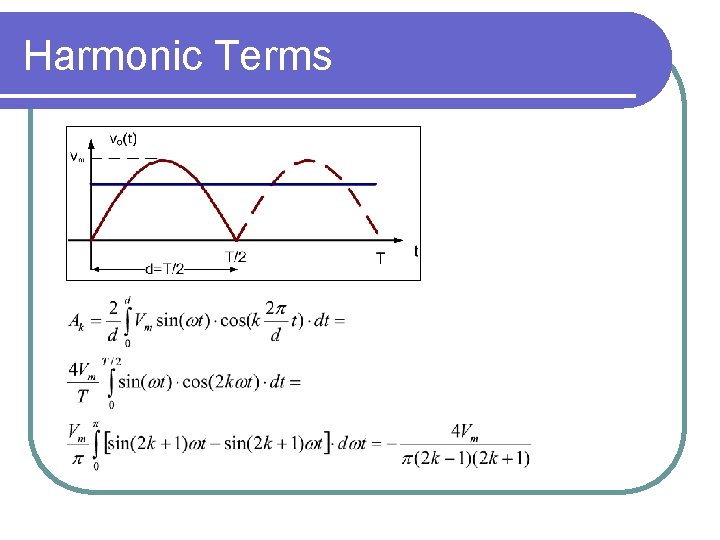
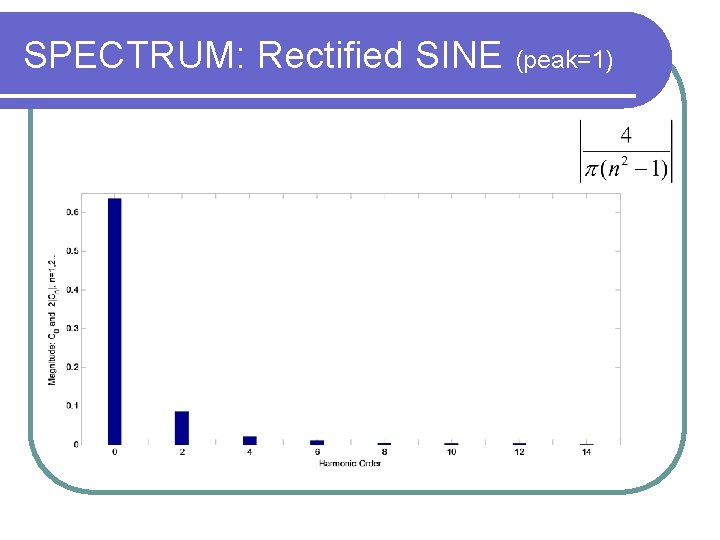
Approximation of the Rectified sine A periodic signal= (constant part)+ (oscillating part)

Average Value

Harmonic Terms

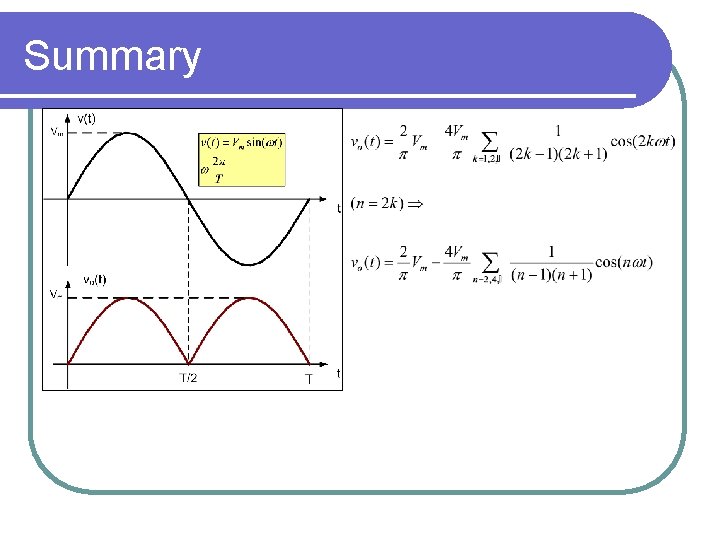
Summary

Numerical Problem: DC Drive

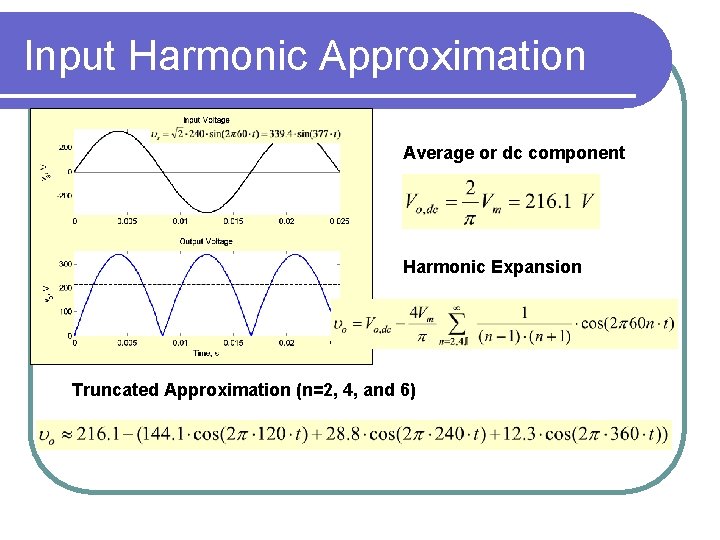
Input Harmonic Approximation Average or dc component Harmonic Expansion Truncated Approximation (n=2, 4, and 6)

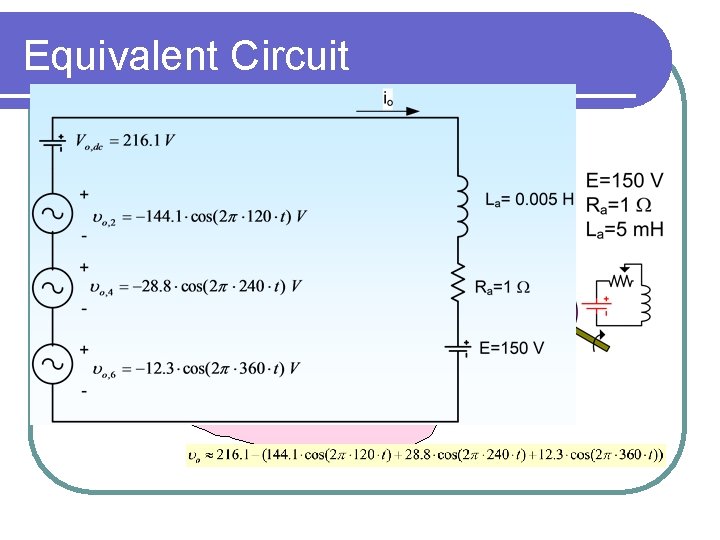
Equivalent Circuit

Superimpose Sources: DC Source

Superposition: n=2, f=120 Hz

Superposition: n=4, f=240 Hz

Superposition: n=6, f=360 Hz

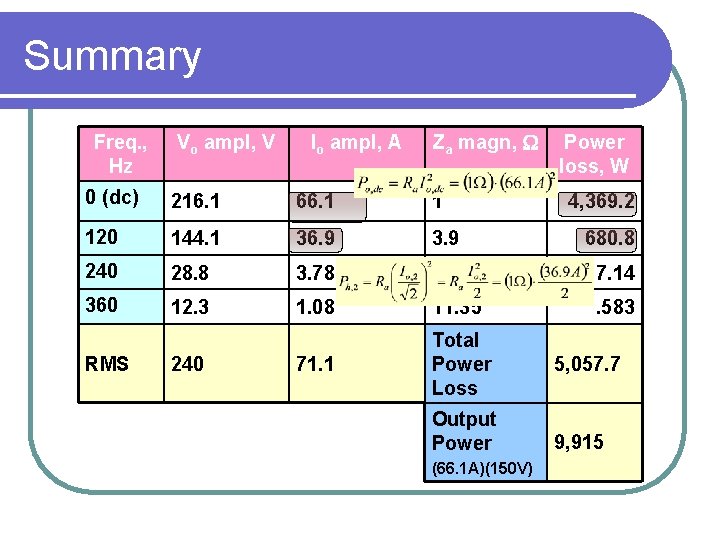
Summary Freq. , Hz Vo ampl, V Io ampl, A Za magn, W Power loss, W 0 (dc) 216. 1 66. 1 1 120 144. 1 36. 9 3. 9 680. 8 240 28. 8 3. 78 7. 61 7. 14 360 12. 3 1. 08 11. 35 . 583 71. 1 Total Power Loss RMS 240 Output Power (66. 1 A)(150 V) 4, 369. 2 5, 057. 7 9, 915

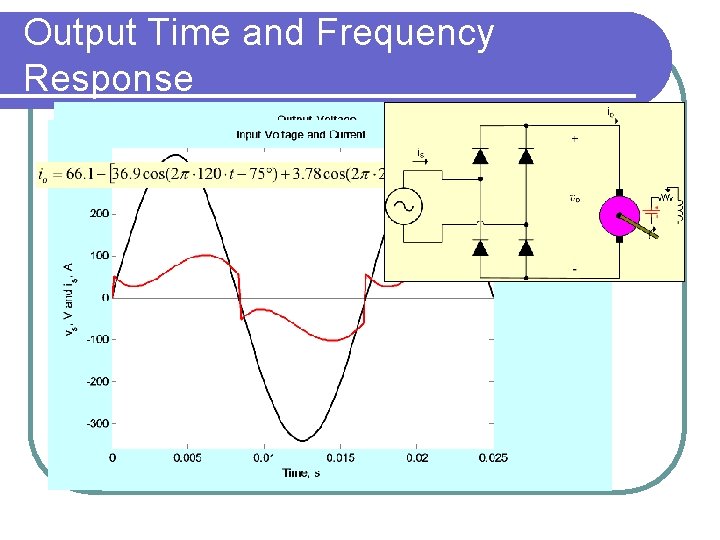
Output Time and Frequency Response

Generalization: Fourier Series The Fourier theorem states that a bounded periodic function f(t) with limited finite number of discontinuities can be described by an infinite series of sine and cosine terms of frequency that is the integer multiple of the fundamental frequency of f(t): Where is the zero frequency or average value of f(t).

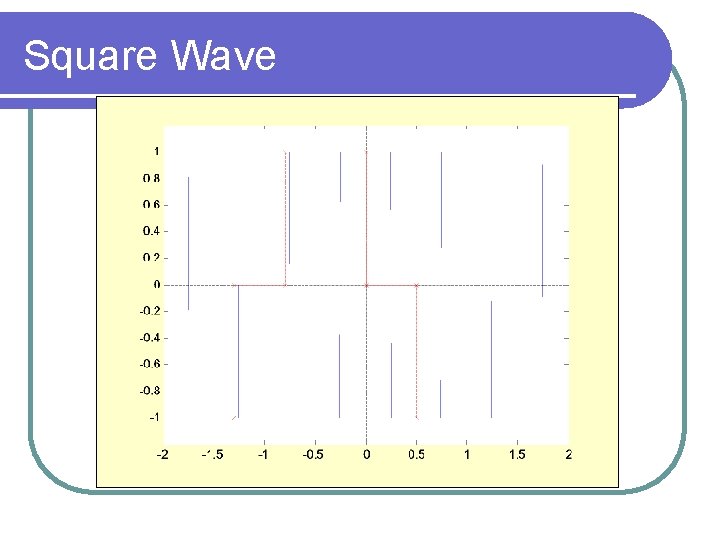
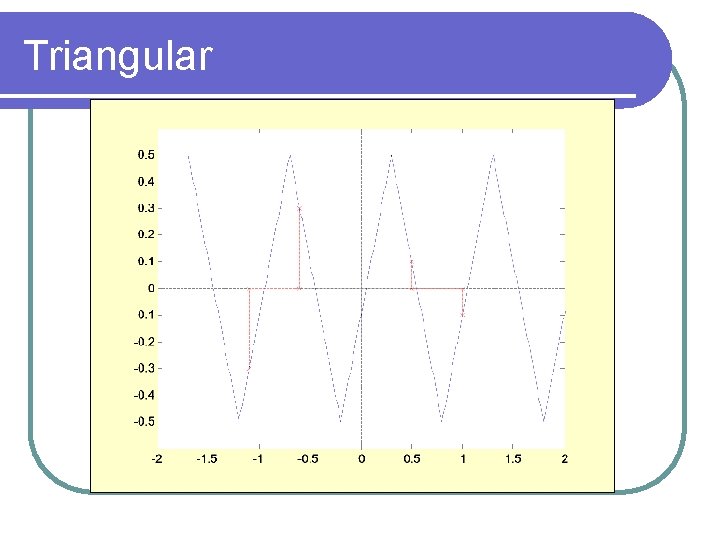
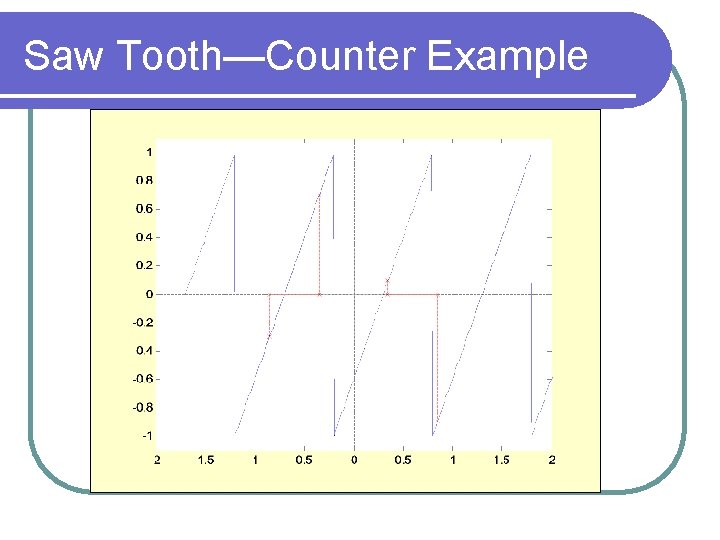
Waveform Symmetry l Half Wave Symmetry l Quarter Wave Symmetry Odd l Even l

Half Wave Symmetry • Half-wave symmetry is independent of the function shift w. r. t the time axis • Even harmonics have zero coefficient

Square Wave

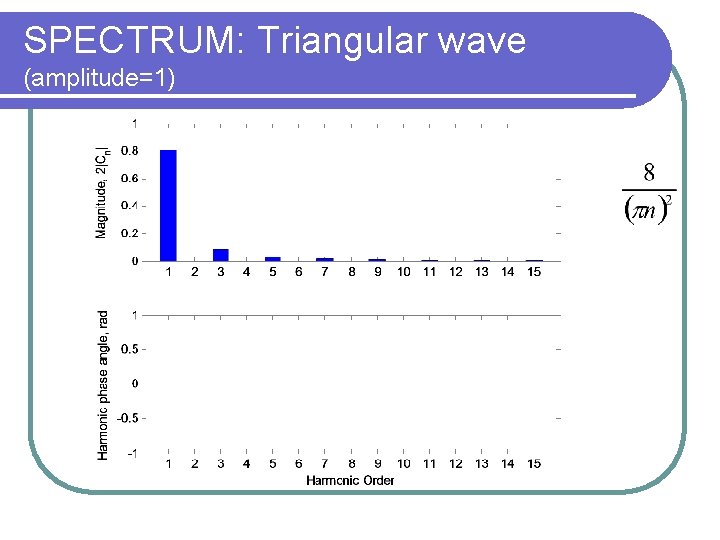
Triangular

Saw Tooth—Counter Example

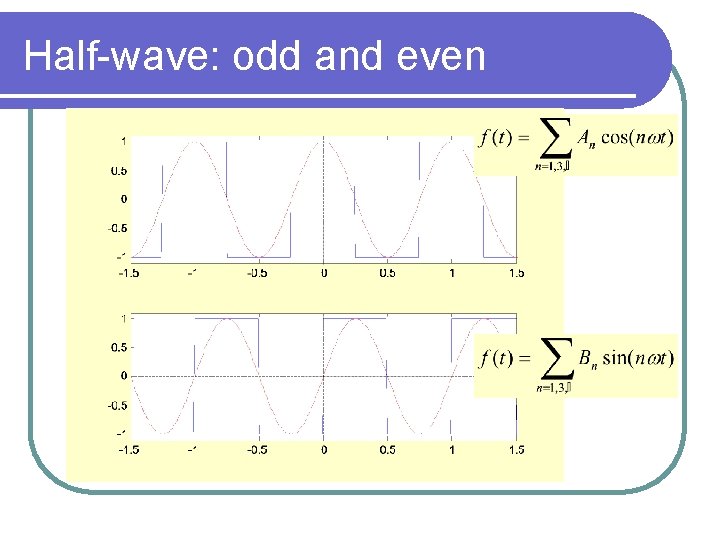
Quarter Wave Symmetry l Half wave and odd symmetry l Half wave and even symmetry

Half-wave: odd and even

Quarter Wave Symmetry Simplification

Forms of the Fourier Transform l Trigonometric l Combined Trigonometric l Exponential

• Trigonometric form • Combined Trigonometric

• Exponential

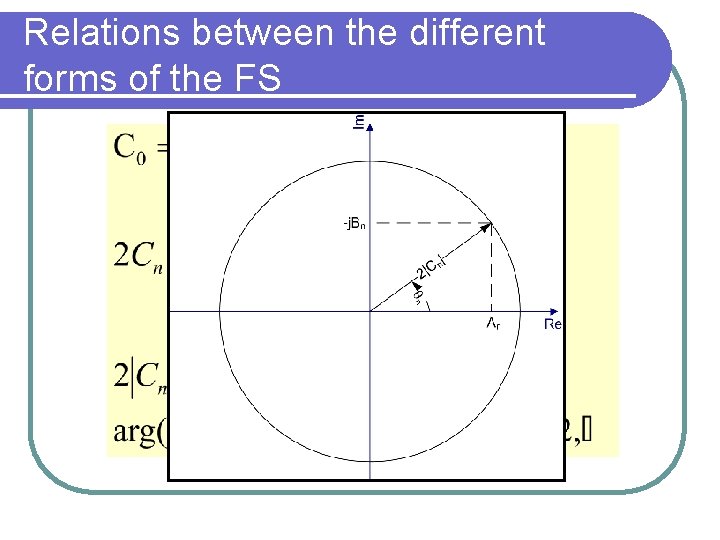
Relations between the different forms of the FS

Summary of FS Formulas

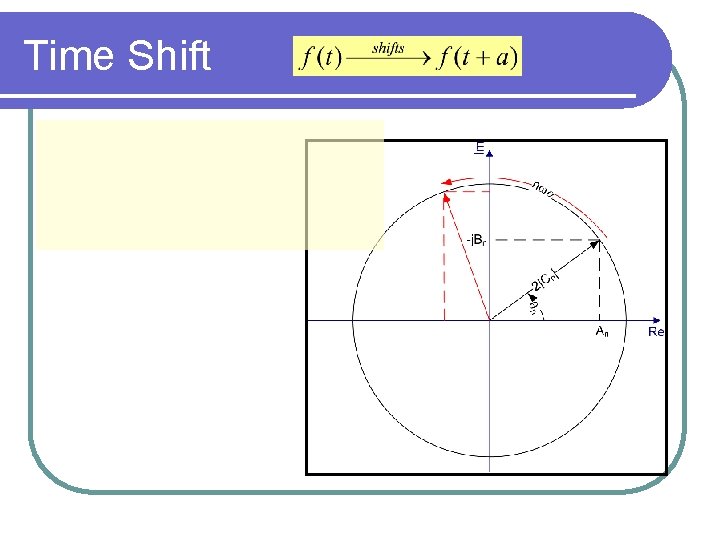
Time Shift

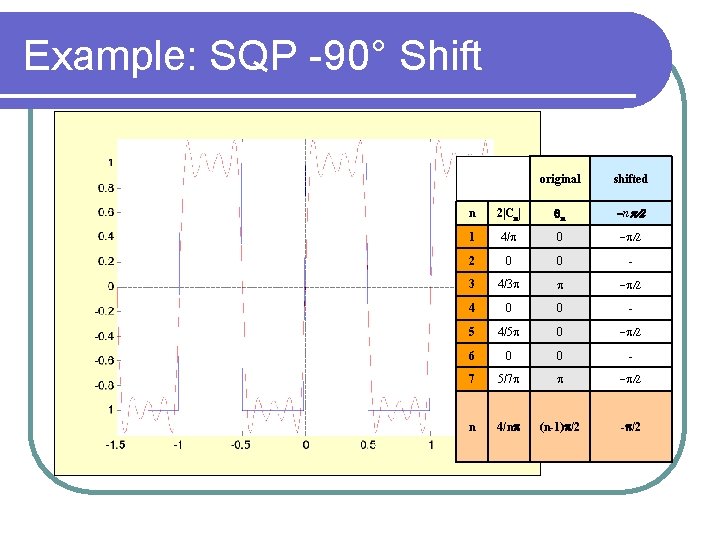
Example: SQP -90° Shift original shifted n 2|Cn| qn -np/2 1 4/p 0 -p/2 2 0 0 - 3 4/3 p p -p/2 4 0 0 - 5 4/5 p 0 -p/2 6 0 0 - 7 5/7 p p -p/2 n 4/np (n-1)p/2 -p/2

Example: SQP -60° Shift original shifted n 2|Cn| qn -np/3 1 4/p 0 -p/3 2 0 0 - 3 4/3 p p 0 4 0 0 - 5 4/5 p 0 p/3 6 0 0 - 7 5/7 p p 2 p/3 n 4/np (n-1)p/2 (n-3)p/6

SPECTRUM: SQ. Pulse (amplitude=1)

SPECTRUM: Sawtooth (amplitude=1)

SPECTRUM: Triangular wave (amplitude=1)

SPECTRUM: Rectified SINE (peak=1)

Using FS to Find the Steady State Response of an LTI System Input periodic, fundamental freq. =f 1=60 Hz Voltage Division

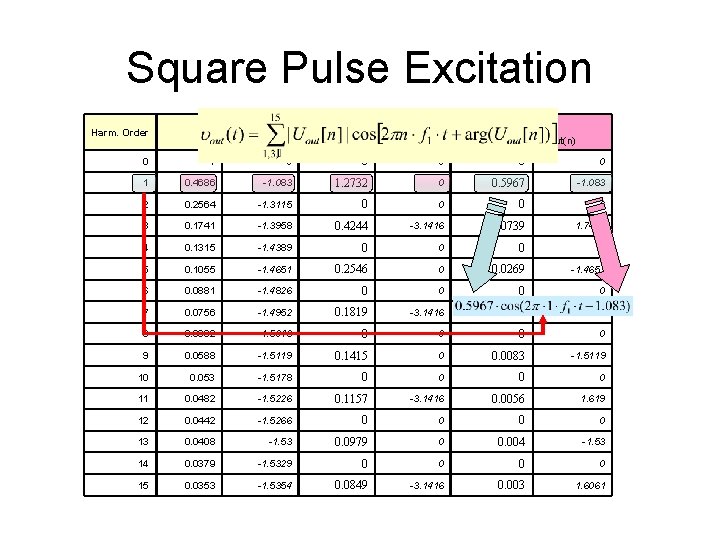
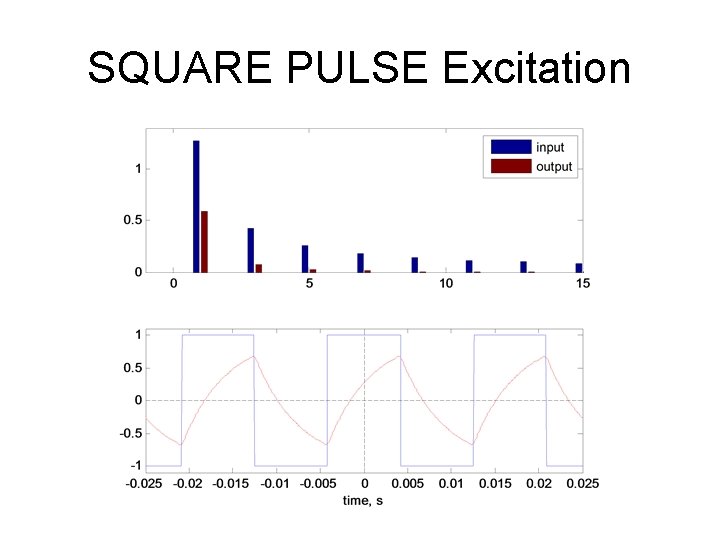
Square Pulse Excitation Harm. Order Inp. |Uin(n)|, <Uin(n) Circ. TF |H(n)|, <H(n) Out. |Uout(n)|, <Uout(n) 0 1 0 0 0 1 0. 4686 -1. 083 1. 2732 0 0. 5967 -1. 083 2 0. 2564 -1. 3115 0 0 3 0. 1741 -1. 3958 0. 4244 -3. 1416 0. 0739 1. 7458 4 0. 1315 -1. 4389 0 0 5 0. 1055 -1. 4651 0. 2546 0 0. 0269 -1. 4651 6 0. 0881 -1. 4826 0 0 7 0. 0756 -1. 4952 0. 1819 -3. 1416 0. 0137 1. 6464 8 0. 0662 -1. 5046 0 0 9 0. 0588 -1. 5119 0. 1415 0 0. 0083 -1. 5119 10 0. 053 -1. 5178 0 0 11 0. 0482 -1. 5226 0. 1157 -3. 1416 0. 0056 1. 619 12 0. 0442 -1. 5266 0 0 13 0. 0408 -1. 53 0. 0979 0 0. 004 -1. 53 14 0. 0379 -1. 5329 0 0 15 0. 0353 -1. 5354 0. 0849 -3. 1416 0. 003 1. 6061

SQUARE PULSE Excitation

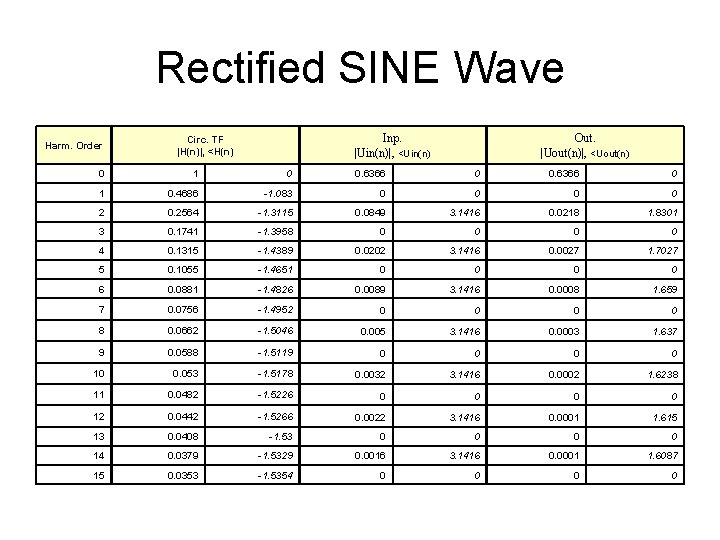
Rectified SINE Wave Harm. Order Inp. |Uin(n)|, <Uin(n) Circ. TF |H(n)|, <H(n) Out. |Uout(n)|, <Uout(n) 0 1 0 0. 6366 0 1 0. 4686 -1. 083 0 0 2 0. 2564 -1. 3115 0. 0849 3. 1416 0. 0218 1. 8301 3 0. 1741 -1. 3958 0 0 4 0. 1315 -1. 4389 0. 0202 3. 1416 0. 0027 1. 7027 5 0. 1055 -1. 4651 0 0 6 0. 0881 -1. 4826 0. 0089 3. 1416 0. 0008 1. 659 7 0. 0756 -1. 4952 0 0 8 0. 0662 -1. 5046 0. 005 3. 1416 0. 0003 1. 637 9 0. 0588 -1. 5119 0 0 10 0. 053 -1. 5178 0. 0032 3. 1416 0. 0002 1. 6238 11 0. 0482 -1. 5226 0 0 12 0. 0442 -1. 5266 0. 0022 3. 1416 0. 0001 1. 615 13 0. 0408 -1. 53 0 0 14 0. 0379 -1. 5329 0. 0016 3. 1416 0. 0001 1. 6087 15 0. 0353 -1. 5354 0 0

Rect. SINE wave

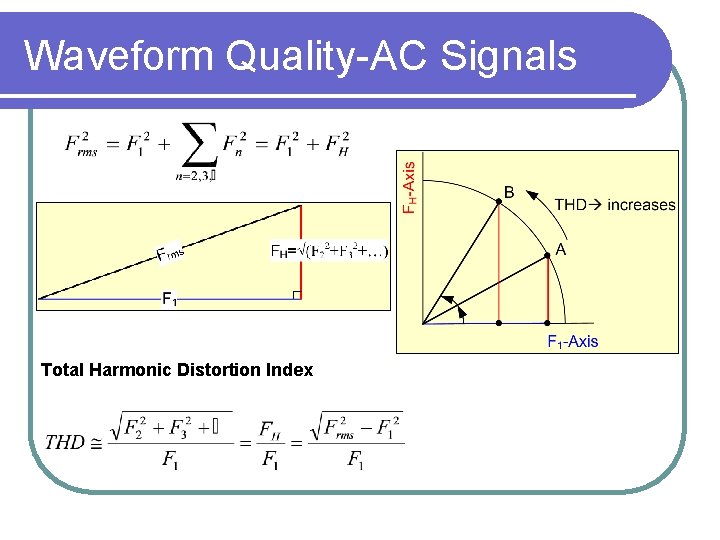
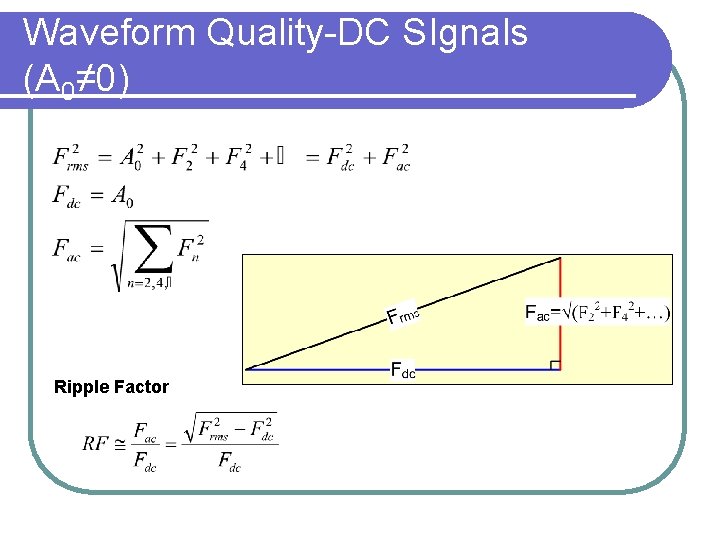
Total RMS of A Signal Rewrite the FS as: Nth harmonic rms (except for n=0) Total rms of the wave form:

Total RMS and the FS Terms Using the orthogonality between the terms: For ac wave forms (A 0=0) it is convenient to write:

Waveform Quality-AC Signals Total Harmonic Distortion Index

Waveform Quality-DC SIgnals (A 0≠ 0) Ripple Factor

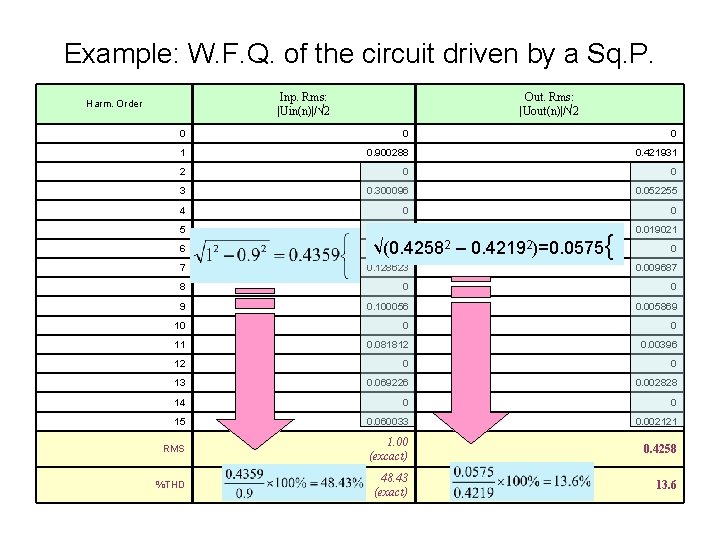
Example: W. F. Q. of the circuit driven by a Sq. P. Inp. Rms: |Uin(n)|/√ 2 Harm. Order Out. Rms: |Uout(n)|/√ 2 0 0 0 1 0. 900288 0. 421931 2 0 0 3 0. 300096 0. 052255 4 0 0 5 0. 180029 0. 019021 6 2 – 0. 42192)=0. 0575{ 0 √(0. 4258 0 7 0. 128623 0. 009687 8 0 0 9 0. 100056 0. 005869 10 0 0 11 0. 081812 0. 00396 12 0 0 13 0. 069226 0. 002828 14 0 0 15 0. 060033 0. 002121 RMS 1. 00 (excact) 0. 4258 %THD 48. 43 (exact) 13. 6

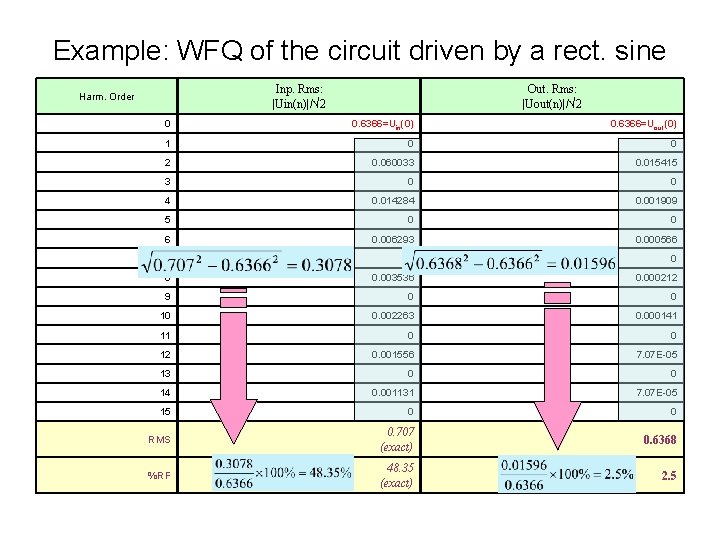
Example: WFQ of the circuit driven by a rect. sine Inp. Rms: |Uin(n)|/√ 2 Harm. Order Out. Rms: |Uout(n)|/√ 2 0 0. 6366=Uin(0) 0. 6366=Uout(0) 1 0 0 2 0. 060033 0. 015415 3 0 0 4 0. 014284 0. 001909 5 0 0 6 0. 006293 0. 000566 7 0 0 8 0. 003536 0. 000212 9 0 0 10 0. 002263 0. 000141 11 0 0 12 0. 001556 7. 07 E-05 13 0 0 14 0. 001131 7. 07 E-05 15 0 0 RMS 0. 707 (exact) 0. 6368 %RF 48. 35 (exact) 2. 5
 Stupid spherical harmonics (sh) tricks
Stupid spherical harmonics (sh) tricks Closed pipe harmonics
Closed pipe harmonics Spherical harmonic lighting: the gritty details
Spherical harmonic lighting: the gritty details Periodic motion formula
Periodic motion formula Open tubes
Open tubes Harmonics formula
Harmonics formula Spherical harmonics formula
Spherical harmonics formula Associated legendre polynomials table
Associated legendre polynomials table Spherical harmonics formula
Spherical harmonics formula Artificial harmonics bass
Artificial harmonics bass K factor harmonics
K factor harmonics Vibraphone harmonics
Vibraphone harmonics Harmonics measurement
Harmonics measurement Harmonics measurement
Harmonics measurement Spherical harmonic lighting
Spherical harmonic lighting Spherical harmonics rotation invariant
Spherical harmonics rotation invariant Spherical harmonics orthogonality
Spherical harmonics orthogonality Union set operation
Union set operation 2160704
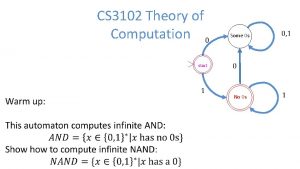
2160704 Transition diagram in theory of computation
Transition diagram in theory of computation Types of languages in theory of computation
Types of languages in theory of computation Theory of computation
Theory of computation Theory of computation
Theory of computation Theory of computation
Theory of computation Introduction to the theory of computation
Introduction to the theory of computation Time complexity hierarchy
Time complexity hierarchy Anbn pda
Anbn pda Theory of computation quiz
Theory of computation quiz Theory of computation
Theory of computation Dfa to nfa
Dfa to nfa The theory of computation
The theory of computation Uva lookup computing id
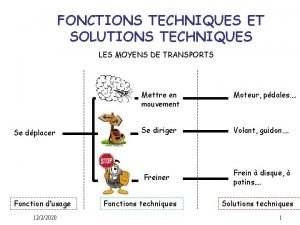
Uva lookup computing id Les fonctions techniques et les solutions techniques
Les fonctions techniques et les solutions techniques Pipetting techniques tutorial
Pipetting techniques tutorial W/tax compensation table
W/tax compensation table Expanded withholding tax computation
Expanded withholding tax computation Expanded withholding tax computation
Expanded withholding tax computation Bir form 1901 job order
Bir form 1901 job order Fertilizer computation philrice
Fertilizer computation philrice Modeling computation discrete math
Modeling computation discrete math Normal tax
Normal tax Income tax computation format
Income tax computation format Crystalloid fluids examples
Crystalloid fluids examples Income tax computation format
Income tax computation format Efficient methods for data cube computation
Efficient methods for data cube computation Drug calculation formula
Drug calculation formula Data cube computation
Data cube computation Data cube computation
Data cube computation Gtts per minute formula
Gtts per minute formula Cuts of a distributed computation
Cuts of a distributed computation Withholding tax form 2307
Withholding tax form 2307 Computation of wealth tax
Computation of wealth tax Board feet computation
Board feet computation The pagerank citation ranking bringing order to the web
The pagerank citation ranking bringing order to the web The pagerank citation ranking: bringing order to the web
The pagerank citation ranking: bringing order to the web Pagerank
Pagerank Binary search in secure computation
Binary search in secure computation Visio shape meanings
Visio shape meanings Supplementary rate in overheads
Supplementary rate in overheads Media computation
Media computation Types of errors in numerical computation
Types of errors in numerical computation Pagerank computation
Pagerank computation Computation examples
Computation examples 7 tuples of pda
7 tuples of pda The purpose of computation is insight not numbers
The purpose of computation is insight not numbers Privacy-enhancing computation
Privacy-enhancing computation Ram model of computation
Ram model of computation Direct computation
Direct computation Common lisp: a gentle introduction to symbolic computation
Common lisp: a gentle introduction to symbolic computation Ridgmount practice ucl
Ridgmount practice ucl Multiparty computation
Multiparty computation Two round multiparty computation via multi-key fhe
Two round multiparty computation via multi-key fhe Computation structures
Computation structures Umut acar cmu
Umut acar cmu Secure multiparty computation
Secure multiparty computation Pmpl cis
Pmpl cis Fertilizer computation
Fertilizer computation Fertilizer computation
Fertilizer computation Computation history
Computation history Hypertensive emergency vs urgency
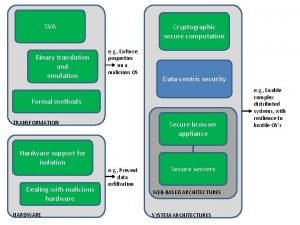
Hypertensive emergency vs urgency Verifiable computation
Verifiable computation Computation history
Computation history Computation examples
Computation examples Fertilizer computation
Fertilizer computation Drop factor formula with example
Drop factor formula with example Message passing paradigm in distributed computing
Message passing paradigm in distributed computing What is differential levelling
What is differential levelling Fertilizer computation examples
Fertilizer computation examples Binary table 1 to 100
Binary table 1 to 100 Mcit tax
Mcit tax Two-player
Two-player Parabon computation
Parabon computation Csci 3130
Csci 3130 Automata theory tutorial
Automata theory tutorial Csc3130
Csc3130 Cyk algorithm
Cyk algorithm Csci3130
Csci3130