CSCI 3130 Formal languages and automata theory Tutorial

Reminder • Homework 4 is due next thursday.

LR(0) parsing • A a • Ab • After reading an ‘a’, the next

LR(0) parsing E E+T | a T b|c Put a dot • in any

LR(0) parsing E • E+T E E • +T E E+ • T E

LR(0) parsing state stack valid items reading action 1 E • E+T, E •

LR(0) parsing: NFA representation q 0 a, b: terminals notation A, B, C: variables

LR(0) parsing: NFA representation E • E+T E E • +T E E+ •

LR(0) parsing: NFA representation q 0 S • For every item S • q

LR(0) parsing: NFA representation A • X X A X • For every item

LR(0) parsing: NFA representation A • C a, b: terminals notation A, B, C:

LR(0) parsing: NFA representation • Convert the NFA to DFA 2 a 1 E

LR(0) parsing: remember state in stack • When we reduce, we have to consider

LR(0) parsing: remember state in stack 2 a 1 E • E+T E •

Slides: 40

Download presentation

CSCI 3130: Formal languages and automata theory Tutorial 6 Chin

Reminder • Homework 4 is due next thursday.

LR(0) parsing • A a • Ab • After reading an ‘a’, the next possible symbol is – A a. A • b Or expanding the ‘A’ (think of aa. Abb) – A • a. Ab – A a • Ab

LR(0) parsing • E E+T | a • T b|c

LR(0) parsing E E+T | a T b|c Put a dot • in any possible positions E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • These are valid items. The bottom ones are complete items. When you see complete items, reduce. T • c T c •

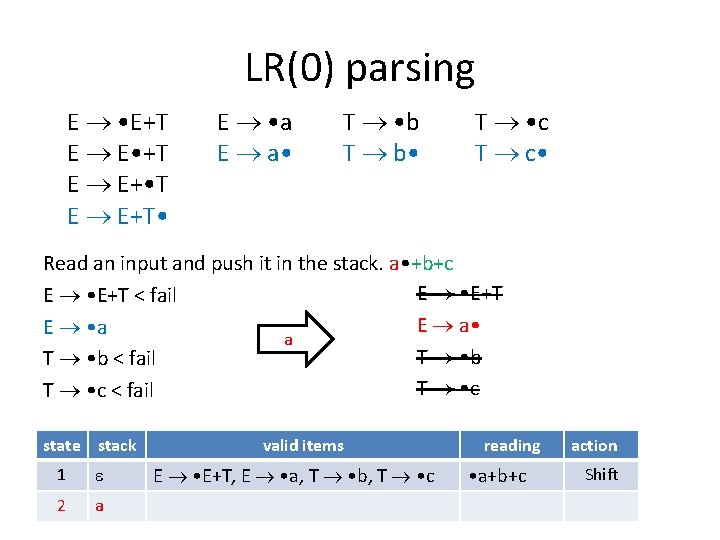
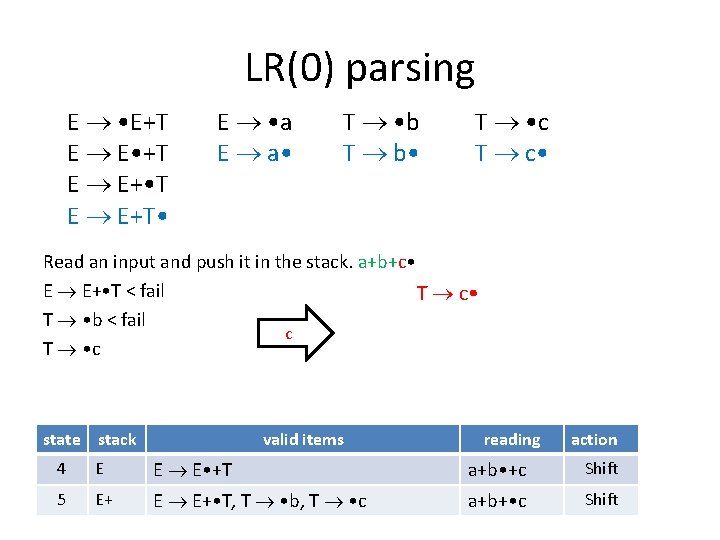
LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • Suppose we are given a+b+c Before reading anything, the valid items are: E • E+T, E • a, T • b, T • c No complete items, shift. state stack 1 valid items E • E+T, E • a, T • b, T • c reading • a+b+c action Shift

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • Read an input and push it in the stack. a • +b+c E • E+T < fail E a • E • a a T • b < fail T • c < fail state stack 1 2 a valid items E • E+T, E • a, T • b, T • c reading • a+b+c action Shift

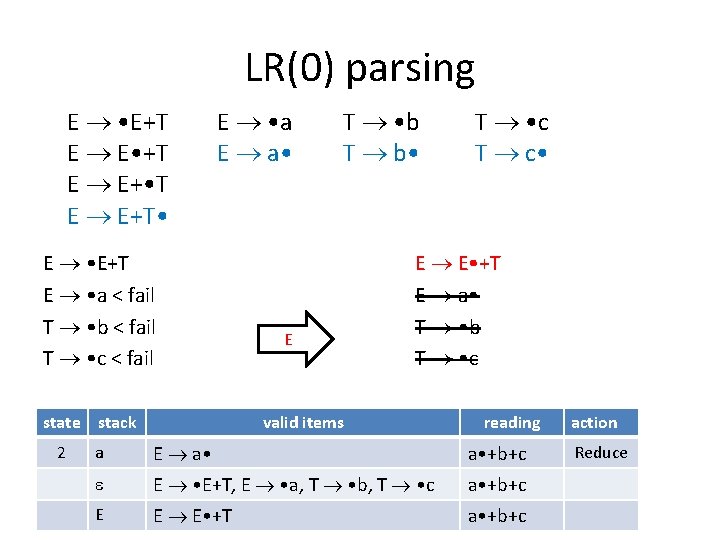
LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • The valid item is E a • When you see exactly one item and it is complete, reduce. * If there are more than 1 complete items, R/R conflict. * If there is another item, but it is not complete, S/R conflict. state stack valid items reading action 1 E • E+T, E • a, T • b, T • c • a+b+c Shift 2 a E a • +b+c Reduce

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • How to reduce: Look at the corresponding complete item (i. e. E a • ) R. H. S. has k symbols, pop k symbols out of the stack (i. e. pop ‘a’) Consider the valid items in corresponding state (i. e. items in state 1) Then push the symbol on the L. H. S. to the stack (i. e. push ‘E’) state stack valid items reading action 1 E • E+T, E • a, T • b, T • c • a+b+c Shift 2 a E a • +b+c Reduce E • E+T, E • a, T • b, T • c E

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • E • E+T E • a < fail T • b < fail T • c < fail state stack 2 T • b T b • E T • c T c • E E • +T E a • T • b T • c valid items reading a E a • +b+c E • E+T, E • a, T • b, T • c a • +b+c E E E • +T a • +b+c action Reduce

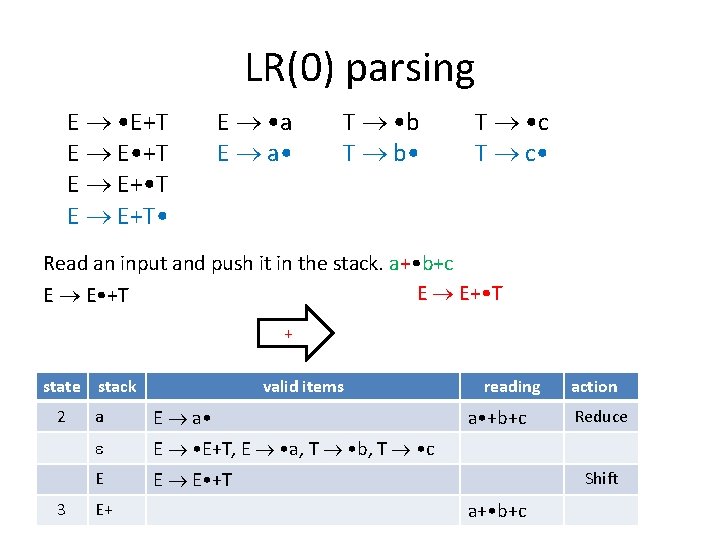
LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • The valid item is: E E • +T No complete items, shift. state stack 2 valid items reading a E a • +b+c E • E+T, E • a, T • b, T • c a • +b+c E E E • +T a • +b+c action Reduce Shift

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • Read an input and push it in the stack. a+ • b+c E E+ • T E E • +T + state stack 2 3 valid items a E a • E+T, E • a, T • b, T • c E E E • +T E+ reading a • +b+c action Reduce Shift a+ • b+c

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • The valid items are E E+ • T T • b <- This comes from expanding T • b T • c <- This comes from expanding T • c No complete items, shift. state stack 2 3 valid items a E a • E+T, E • a, T • b, T • c E E E • +T E+ E E+ • T, T • b, T • c reading a • +b+c action Reduce Shift a+ • b+c Shift

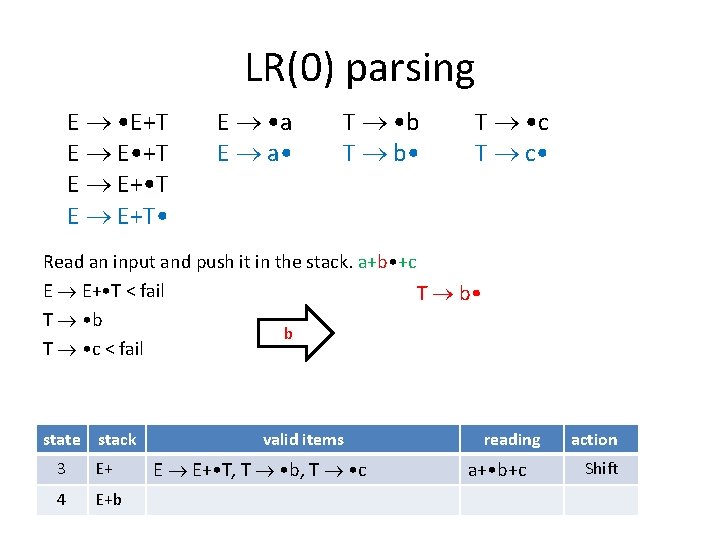
LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • Read an input and push it in the stack. a+b • +c E E+ • T < fail T b • T • b b T • c < fail state stack 3 E+ 4 E+b valid items E E+ • T, T • b, T • c reading a+ • b+c action Shift

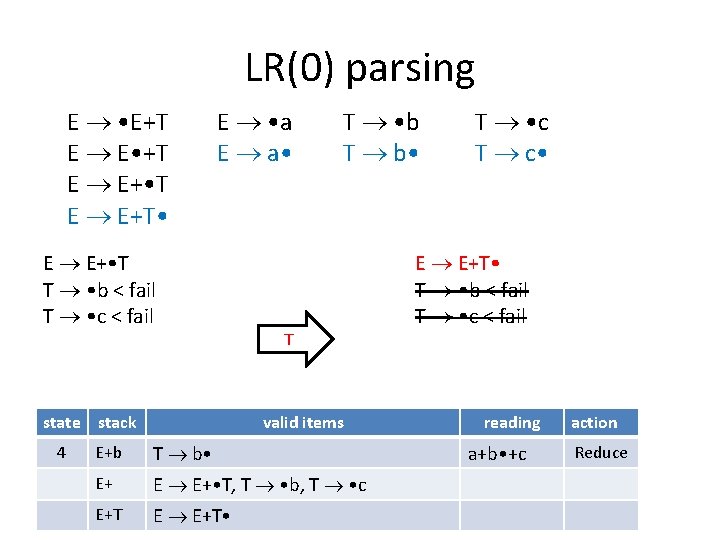
LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • The valid item is T b • When you see exactly one item and it is complete, reduce. state stack valid items reading action 3 E+ E E+ • T, T • b, T • c a+ • b+c Shift 4 E+b T b • a+b • +c Reduce

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • How to reduce: Look at the corresponding complete item (i. e. T b • ) R. H. S. has k symbols, pop k symbols out of the stack (i. e. pop ‘b’) Consider the valid items in corresponding state (i. e. items in state 3) Then push the symbol on the L. H. S. to the stack (i. e. push ‘T’) state stack valid items reading action 3 E+ E E+ • T, T • b, T • c a+ • b+c Shift 4 E+b T b • a+b • +c Reduce E+ E E+ • T, T • b, T • c E+T

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • E E+ • T T • b < fail T • c < fail state stack 4 T • b T b • T valid items E+b T b • E+ E E+ • T, T • b, T • c E+T E E+T • T • c T c • E E+T • T • b < fail T • c < fail reading a+b • +c action Reduce

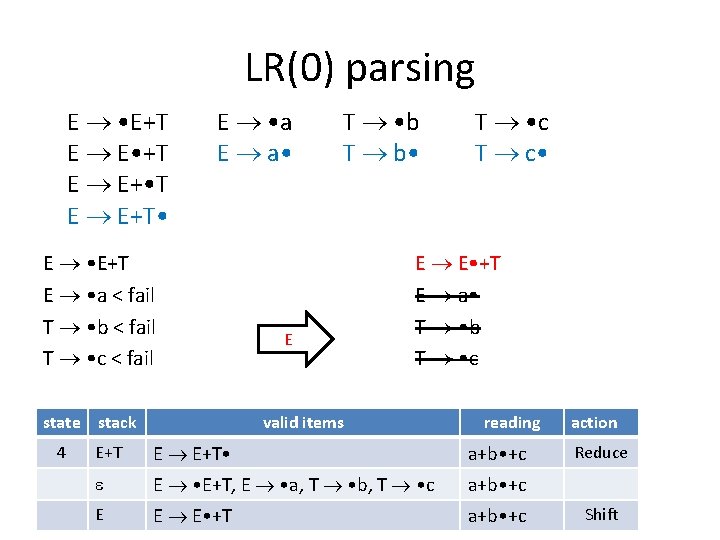
LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • The valid item is E E+T • When you see exactly one item and it is complete, reduce. state stack 4 valid items E+b T b • E+ E E+ • T, T • b, T • c E+T E E+T • reading a+b • +c action Reduce

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • How to reduce: Look at the corresponding complete item (i. e. E E+T • ) R. H. S. has k symbols, pop k symbols out of the stack (i. e. pop ‘E+T’) Consider the valid items in corresponding state (i. e. items in state 1) Then push the symbol on the L. H. S. to the stack (i. e. push ‘E’) state stack 1 valid items E • E+T, E • a, T • b, T • c E+T E E+T • E+T, E • a, T • b, T • c reading • a+b+c action Shift … 4 E Reduce

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • E • E+T E • a < fail T • b < fail T • c < fail state stack 4 T • b T b • E T • c T c • E E • +T E a • T • b T • c valid items reading E+T E E+T • a+b • +c E • E+T, E • a, T • b, T • c a+b • +c E E E • +T a+b • +c action Reduce Shift

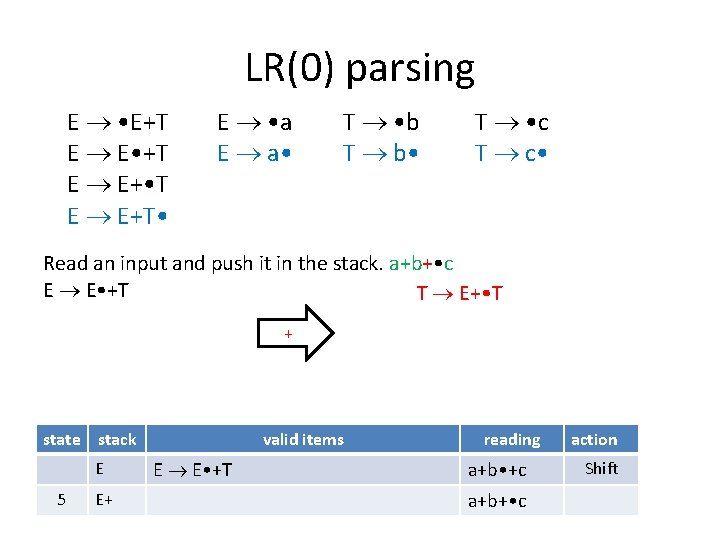
LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • The valid item is: E E • +T No complete items, shift. state stack 4 valid items reading E+T E E+T • a+b • +c E • E+T, E • a, T • b, T • c a+b • +c E E E • +T a+b • +c action Reduce Shift

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • Read an input and push it in the stack. a+b+ • c E E • +T T E+ • T + state stack E 5 E+ valid items E E • +T reading a+b • +c a+b+ • c action Shift

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • The valid items are E E+ • T T • b <- This comes from expanding T • b T • c <- This comes from expanding T • c No complete items, shift. state stack 5 valid items reading action E E E • +T a+b • +c Shift E+ E E+ • T, T • b, T • c a+b+ • c Shift

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • Read an input and push it in the stack. a+b+c • E E+ • T < fail T c • T • b < fail c T • c state stack valid items reading action 4 E E E • +T a+b • +c Shift 5 E+ E E+ • T, T • b, T • c a+b+ • c Shift

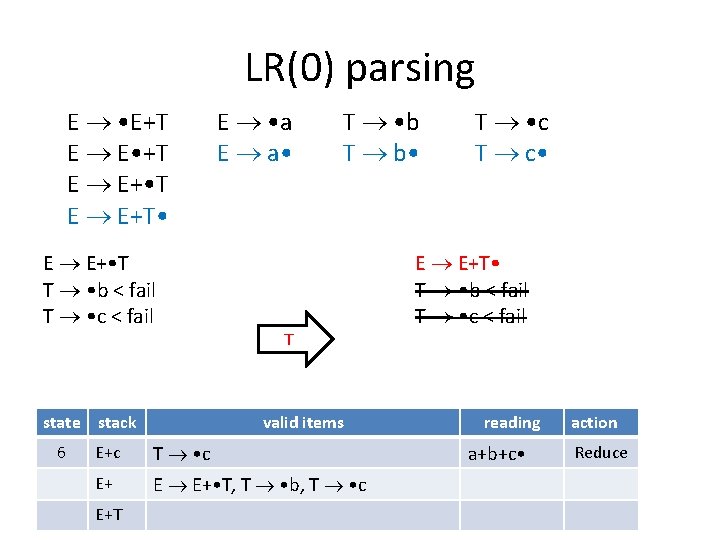
LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • The valid item is T c • When you see exactly one item and it is complete, reduce. state stack valid items reading action 5 E+ E E+ • T, T • b, T • c a+b+ • c Shift 6 E+c T • c a+b+c • Reduce

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • How to reduce: Look at the corresponding complete item (i. e. T c • ) R. H. S. has k symbols, pop k symbols out of the stack. (i. e. pop ‘c’) Consider the valid items in corresponding state (i. e. items in state 5) Then push the symbol on the L. H. S. to the stack (i. e. push ‘T’) state stack 6 valid items E+c T • c E+ E E+ • T, T • b, T • c E+T reading a+b+c • action Reduce

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E E+ • T T • b < fail T • c < fail state stack 6 E • a E a • T • b T b • T valid items E+c T • c E+ E E+ • T, T • b, T • c E+T T • c T c • E E+T • T • b < fail T • c < fail reading a+b+c • action Reduce

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • The valid item is E E+T • When you see exactly one item and it is complete, reduce. state stack 6 valid items E+c T • c E+ E E+ • T, T • b, T • c E+T E E+T • reading a+b+c • action Reduce

LR(0) parsing E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • How to reduce: Look at the corresponding complete item (i. e. E E+T • ) R. H. S. has k symbols, pop k symbols out of the stack. (i. e. pop ‘E+T’) Consider the valid items in corresponding state (i. e. items in state 1) Then push the symbol on the L. H. S. to the stack (i. e. push ‘E’) state stack valid items E • E+T, E • a, T • b, T • c 6 E+ E E+ • T, T • b, T • c 6 E+T E E+T • 1 reading • a+b+c action Shift … 6 Reduce

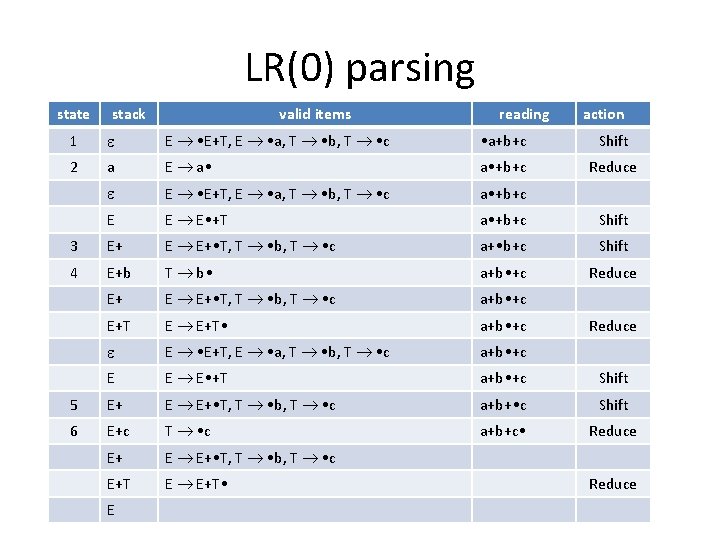
LR(0) parsing state stack valid items reading action 1 E • E+T, E • a, T • b, T • c • a+b+c Shift 2 a E a • +b+c Reduce E • E+T, E • a, T • b, T • c a • +b+c E E E • +T a • +b+c Shift 3 E+ E E+ • T, T • b, T • c a+ • b+c Shift 4 E+b T b • a+b • +c Reduce E+ E E+ • T, T • b, T • c a+b • +c E+T E E+T • a+b • +c Reduce a+b • +c Shift a+b+ • c Shift a+b+c • Reduce 5 E+ E • a E • E+T, E • a, T • b, T • c E a • T • b E E • +T E E+ • T, T • b, T • c T b • 6 E+c T • c E+ E E+ • T, T • b, T • c E+T E E+T • E E T • c a+b • +c T c • Reduce

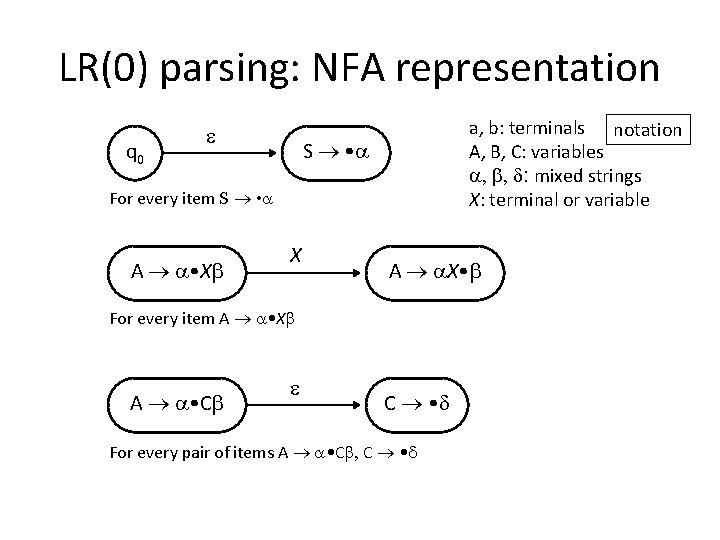
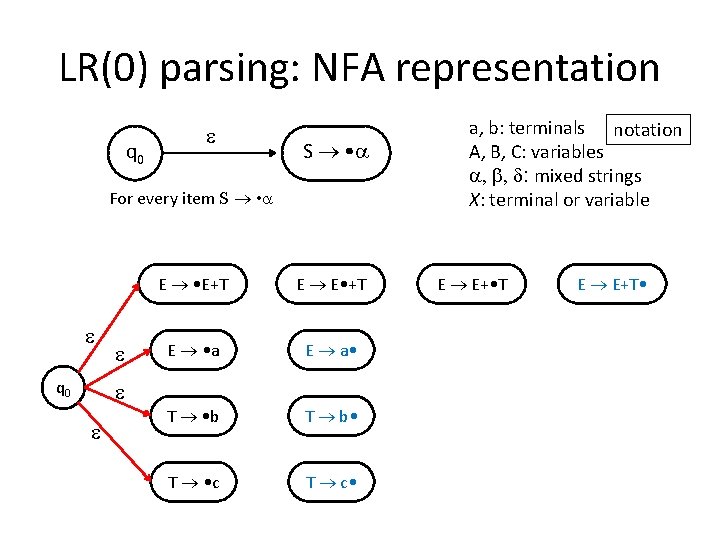
LR(0) parsing: NFA representation q 0 a, b: terminals notation A, B, C: variables , , d: mixed strings X: terminal or variable S • For every item S • A • X X A X • For every item A • X A • C C • d For every pair of items A • C , C • d

LR(0) parsing: NFA representation E • E+T E E • +T E E+ • T E E+T • E • a E a • T • b T b • T • c T c • 1. Each of these items is a state E • E+T E E • +T E • a E a • T • c T c • T • b T b • q 0 E E+ • T E E+T •

LR(0) parsing: NFA representation q 0 S • For every item S • q 0 E • E+T E E • +T E • a E a • T • b T b • T • c T c • a, b: terminals notation A, B, C: variables , , d: mixed strings X: terminal or variable E E+ • T E E+T •

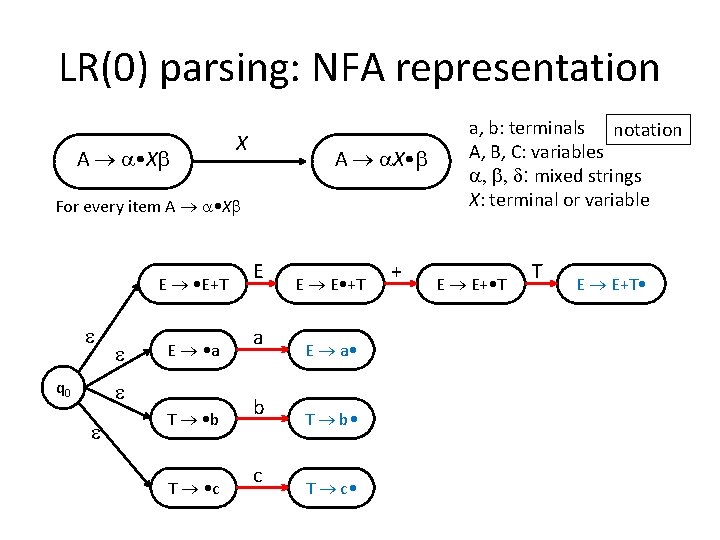
LR(0) parsing: NFA representation A • X X A X • For every item A • X E • E+T q 0 E • a T • b T • c E a b c E E • +T E a • T b • T c • + a, b: terminals notation A, B, C: variables , , d: mixed strings X: terminal or variable E E+ • T T E E+T •

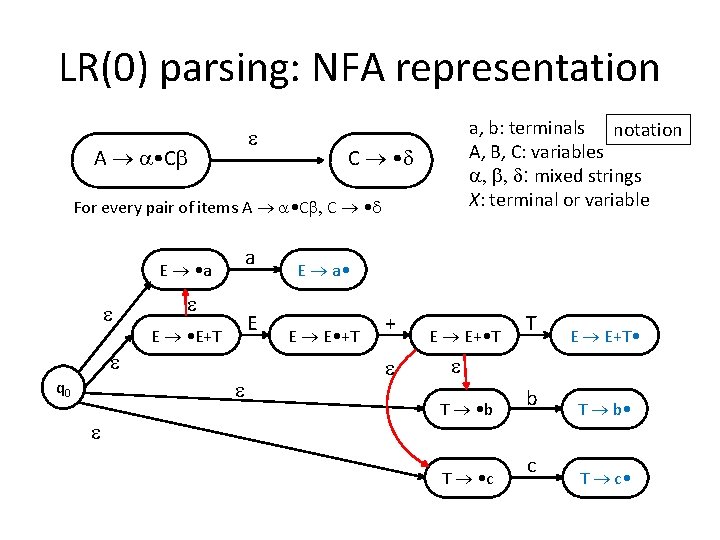
LR(0) parsing: NFA representation A • C a, b: terminals notation A, B, C: variables , , d: mixed strings X: terminal or variable C • d For every pair of items A • C , C • d a E • a E E • E+T q 0 E a • E E • +T + E E+ • T T E E+T • T • b T • c b c T b • T c •

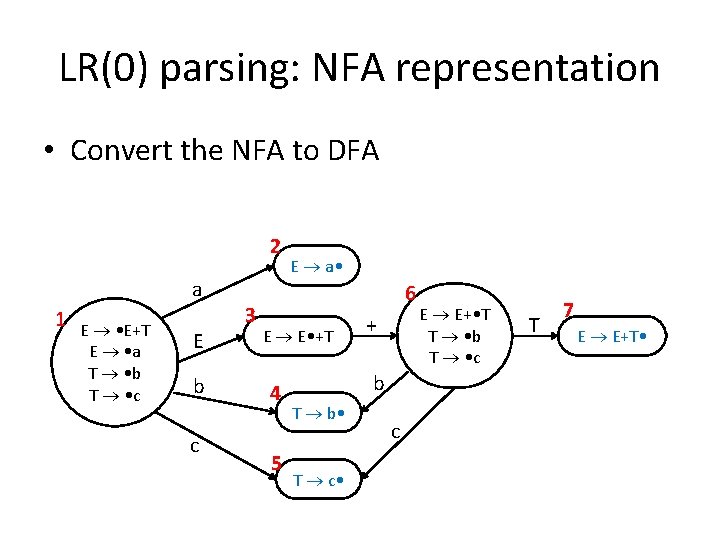
LR(0) parsing: NFA representation • Convert the NFA to DFA 2 a 1 E • E+T E • a T • b T • c E b c 3 E a • 6 E E • +T 4 5 + b T b • T c • c E E+ • T T • b T • c T 7 E E+T •

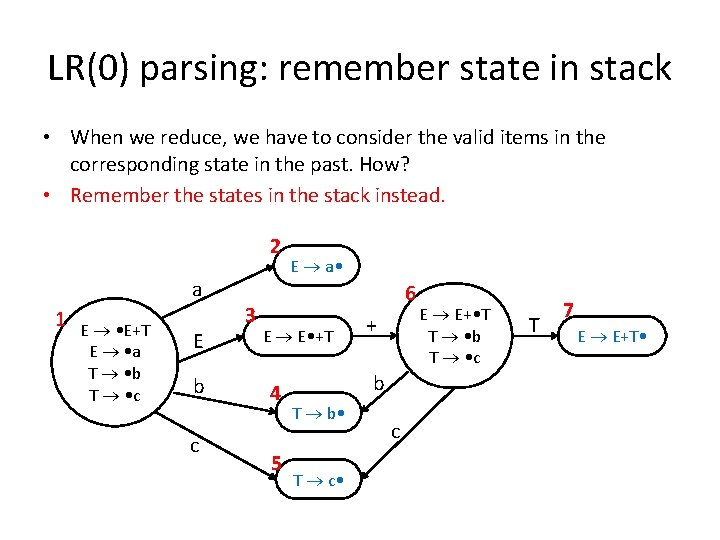
LR(0) parsing: remember state in stack • When we reduce, we have to consider the valid items in the corresponding state in the past. How? • Remember the states in the stack instead. 2 a 1 E • E+T E • a T • b T • c E b c 3 E a • 6 E E • +T 4 5 + b T b • T c • c E E+ • T T • b T • c T 7 E E+T •

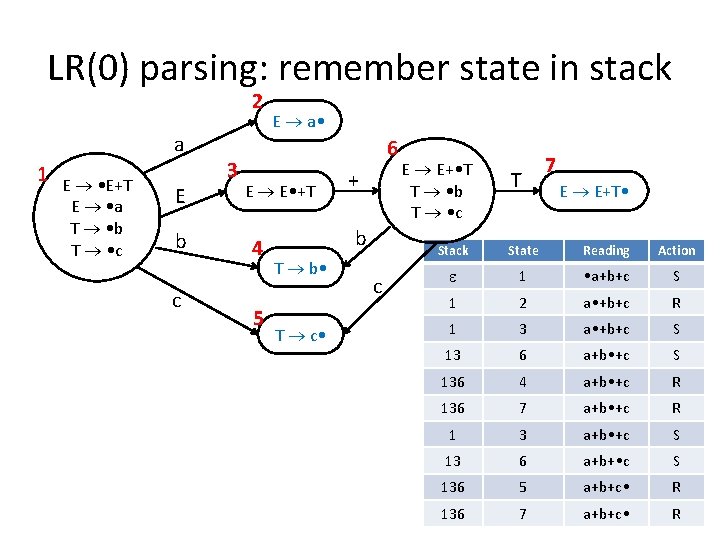
LR(0) parsing: remember state in stack 2 a 1 E • E+T E • a T • b T • c E b c 3 E a • 6 E E • +T 4 5 + b T b • T c • c E E+ • T T • b T • c T 7 E E+T • Stack State Reading Action 1 • a+b+c S 1 2 a • +b+c R 1 3 a • +b+c S 13 6 a+b • +c S 136 4 a+b • +c R 136 7 a+b • +c R 1 3 a+b • +c S 13 6 a+b+ • c S 136 5 a+b+c • R 136 7 a+b+c • R

End • Questions?