CSC 3130 Automata theory and formal languages Tutorial

CSC 3130: Automata theory and formal languages Tutorial 4 KN Hung Office: SHB 1026 Department of Computer Science & Engineering 1

Agenda • Context Free Grammar (CFG) – Design – Parse Tree • Cocke-Younger-Kasami (CYK) algorithm – Parsing CFG in normal form • Pushdown Automata (PDA) – Design 2

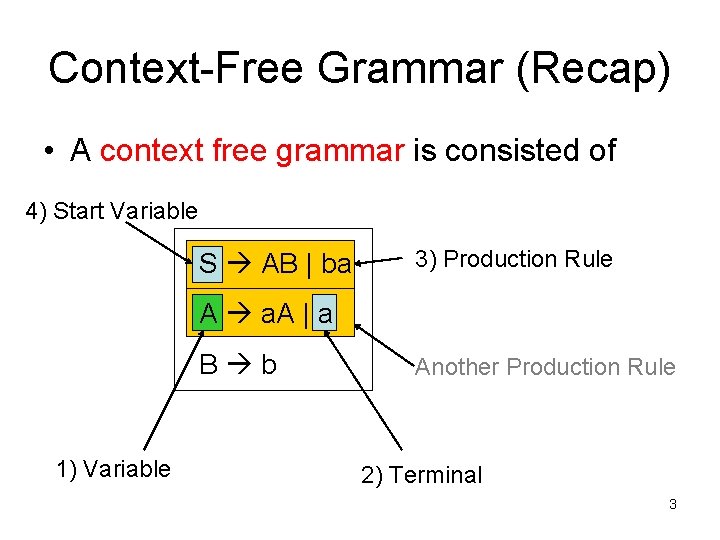
Context-Free Grammar (Recap) • A context free grammar is consisted of 4) Start Variable S AB | ba 3) Production Rule A a. A | a B b 1) Variable Another Production Rule 2) Terminal 3

Context-Free Grammar (Recap) • A string is said to belong to the language (of the CFG) if it can be derived from the start variable = Apply Production Rule CFG Example Derivation S AB | ba S AB A a. A | a a. AB B b aa. B Therefore, aab belongs to the language aab 4

Why CFG? • L = {w = 0 n 1 n : n is an positive integer} • L is not a regular language – Proved by “Pumping Lemma” • A Context-Free Grammar can describe it S 0 S 1 S 01 • Thus, CFG is more general than regular expression – NFA Regular Expression DFA 5

CFG Design • Given a context-free language, design the CFG • L = { ab-string, w : Number of a’s < Number of b’s } • Some time for you to get into think… 1 min S ? … 6

CFG Design (Con’t) • Trial: Bottom-up – Shortest string in L : “b” – Given a string in L, we can expand it, s. t. it is still in L – i. e. , Add terminals, while not violating the constraints 7

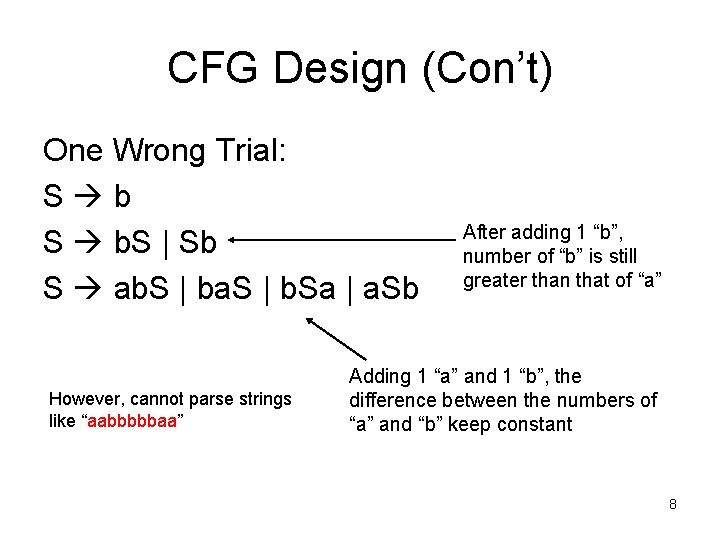
CFG Design (Con’t) One Wrong Trial: S b S b. S | Sb S ab. S | ba. S | b. Sa | a. Sb However, cannot parse strings like “aabbbbbaa” After adding 1 “b”, number of “b” is still greater than that of “a” Adding 1 “a” and 1 “b”, the difference between the numbers of “a” and “b” keep constant 8

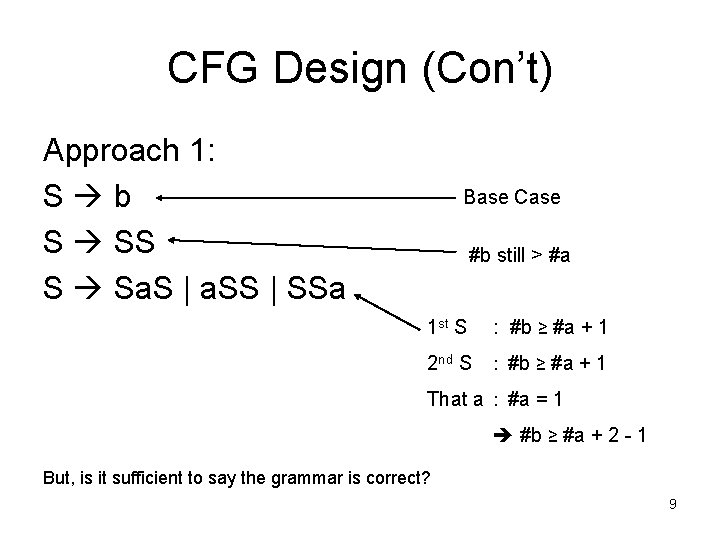
CFG Design (Con’t) Approach 1: S b S SS S Sa. S | a. SS | SSa Base Case #b still > #a 1 st S : #b ≥ #a + 1 2 nd S : #b ≥ #a + 1 That a : #a = 1 #b ≥ #a + 2 - 1 But, is it sufficient to say the grammar is correct? 9

CFG Design (Con’t) Approach 2: • Start with the grammar for ab-strings with same number of a’s and b’s • Call the start symbol of this grammar E • Now, we generate all strings of type Eb. E | Eb. Eb. E | … • Thus, we have the grammar… 10

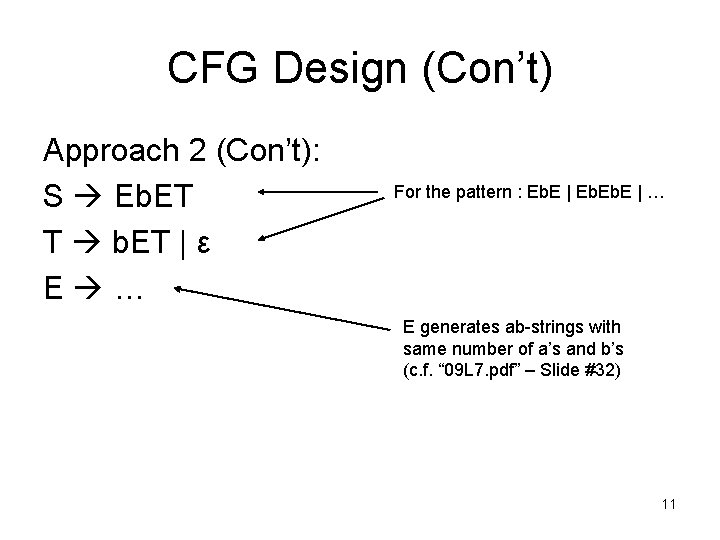
CFG Design (Con’t) Approach 2 (Con’t): S Eb. ET T b. ET | ε E … For the pattern : Eb. E | … E generates ab-strings with same number of a’s and b’s (c. f. “ 09 L 7. pdf” – Slide #32) 11

CFG Design (Con’t) • After designing the grammar, G, you may have to prove (if required) that the language of this grammar is equivalent to the given language • i. e. , Prove that L(G) = L • Proof Part 1) L(G) ⊂ L Part 2) L ⊂ L(G) • Due to time limit, I will not do this part 12

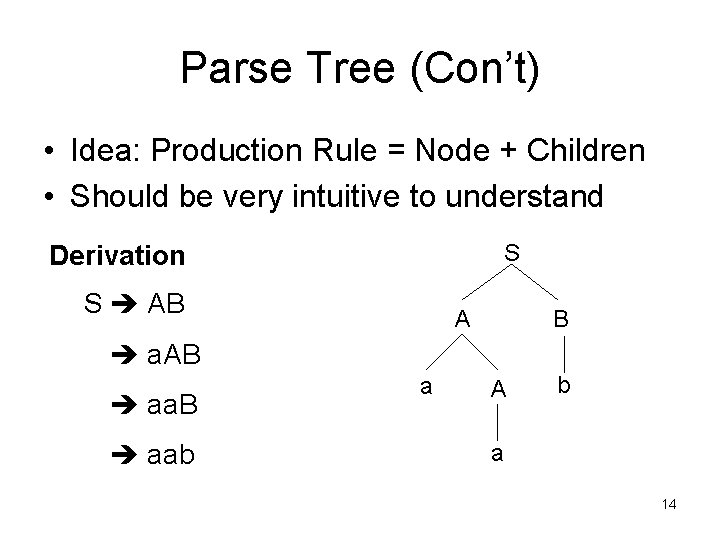
Parse Tree • How to parse “aab” in this grammar? (Previous example) CFG Example Derivation S AB | ba S AB A a. A | a a. AB B b aa. B aab 13

Parse Tree (Con’t) • Idea: Production Rule = Node + Children • Should be very intuitive to understand S Derivation S AB A B a. AB aab a A b a 14

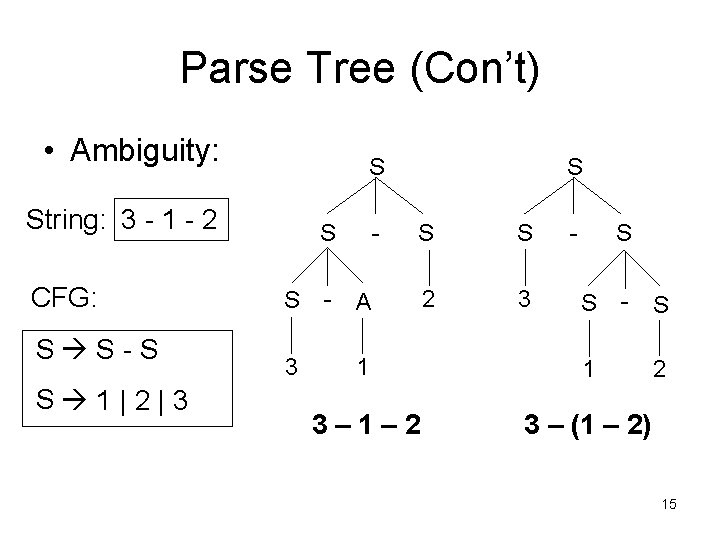
Parse Tree (Con’t) • Ambiguity: S String: 3 - 1 - 2 CFG: S S-S S 1|2|3 S S 3 - - S S S 2 3 A - S S - 1 1 3– 1– 2 3 – (1 – 2) S 2 15

Parse Tree (Con’t) • Useful in programming language – CSC 3180 • Useful in compiler – CSC 3120 16

Cocke-Younger-Kasami Algorithm • Used to parse context-free grammar in Chomsky normal form (or simply normal form) Normal Form Example Every production is of type S AB | BC 1) X YZ A BA | a 2) X a B CC | b 3) S ε C AB | a 17

CYK Algorithm - Idea • = Algorithm 2 in Lecture Note (09 L 8. pdf) • Idea: Bottom Up Parsing • Algorithm: Given a string s of length N For k = 1 to N For every substring of length k Determine what variable(s) can derive it • sub(x, y) : starts at index x, ends at index y 18

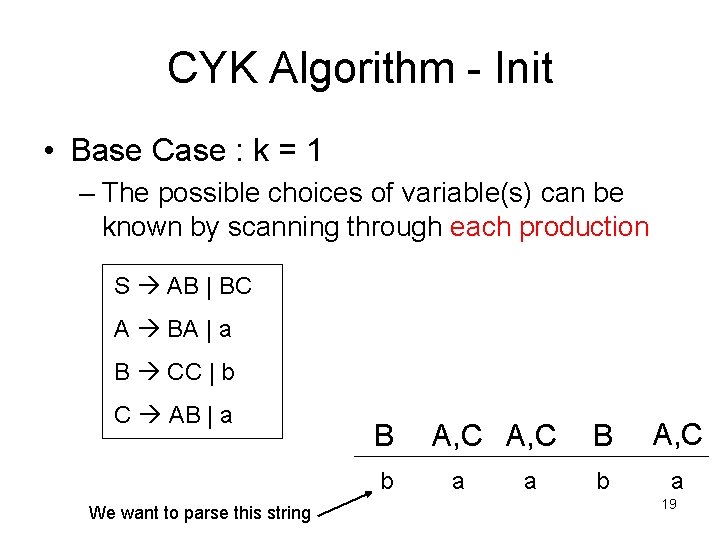
CYK Algorithm - Init • Base Case : k = 1 – The possible choices of variable(s) can be known by scanning through each production S AB | BC A BA | a B CC | b C AB | a B b We want to parse this string A, C a a B A, C b a 19

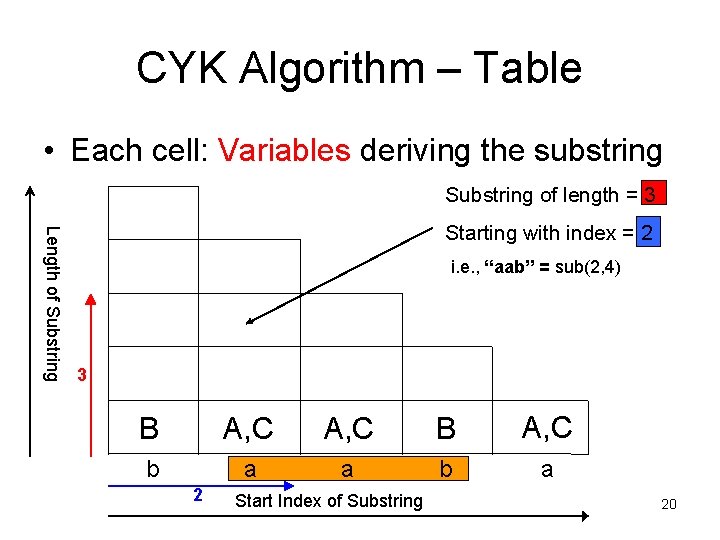
CYK Algorithm – Table • Each cell: Variables deriving the substring Substring of length = 3 Length of Substring Starting with index = 2 i. e. , “aab” = sub(2, 4) 3 B A, C b a a b a 2 Start Index of Substring 20

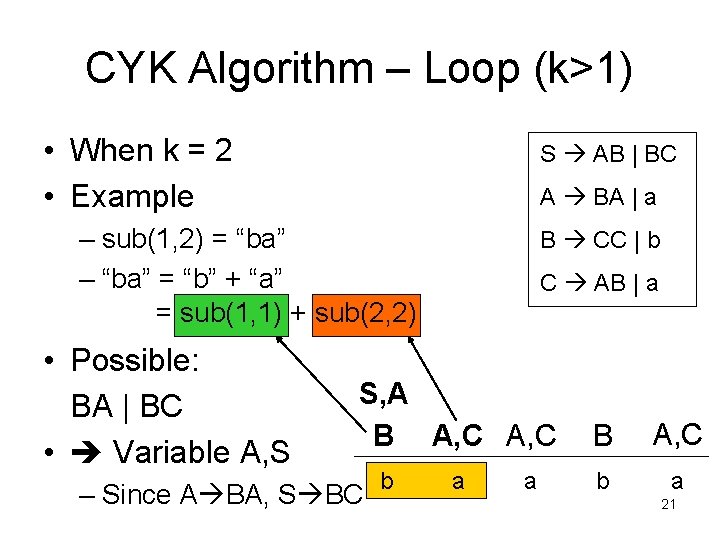
CYK Algorithm – Loop (k>1) • When k = 2 • Example S AB | BC A BA | a – sub(1, 2) = “ba” – “ba” = “b” + “a” = sub(1, 1) + sub(2, 2) • Possible: BA | BC • Variable A, S B CC | b C AB | a S, A B A, C – Since A BA, S BC b a a B A, C b a 21

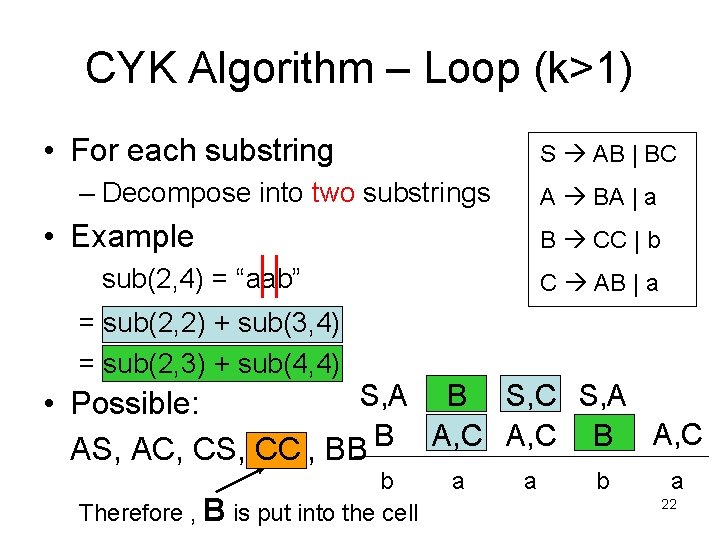
CYK Algorithm – Loop (k>1) • For each substring S AB | BC – Decompose into two substrings A BA | a • Example B CC | b sub(2, 4) = “aab” C AB | a = sub(2, 2) + sub(3, 4) = sub(2, 3) + sub(4, 4) S, A B S, C S, A • Possible: A, C B AS, AC, CS, CC , BB b Therefore , B is put into the cell a a b a 22

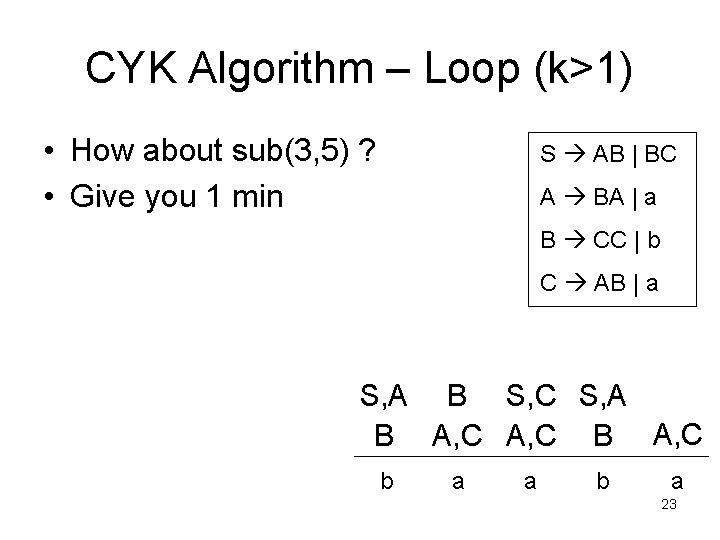
CYK Algorithm – Loop (k>1) • How about sub(3, 5) ? • Give you 1 min S AB | BC A BA | a B CC | b C AB | a S, A B S, C S, A B A, C b a a b a 23

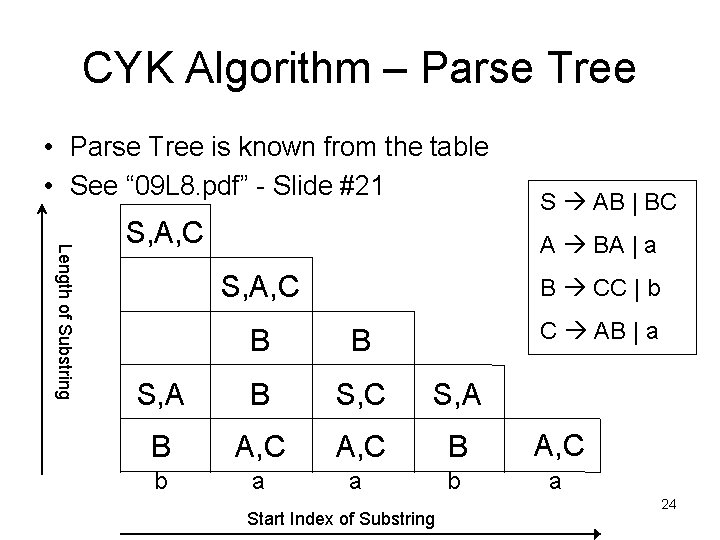
CYK Algorithm – Parse Tree • Parse Tree is known from the table • See “ 09 L 8. pdf” - Slide #21 Length of Substring S, A, C S AB | BC A BA | a S, A, C B CC | b C AB | a B B S, A B S, C S, A B A, C b a a b a Start Index of Substring 24

CYK Algorithm (Conclusion) • Start from shortest substring to the longest – i. e. , from single-character-string to the whole string • For Context-free grammar, G 1) Convert G into normal form • Remove ε-productions • Remove unit-productions 2) Apply CYK algorithm • Con: Loss in intuition 25

End • Thanks for coming! =] • Any questions? 26