7 Angular Momentum 7 A Angular Momentum Commutation





































- Slides: 37

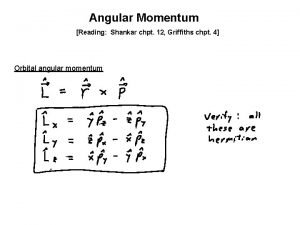
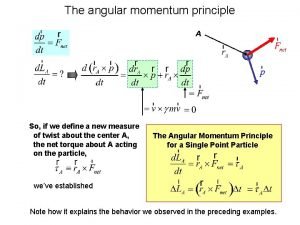
7. Angular Momentum 7 A. Angular Momentum Commutation Why it doesn’t commute • The order in which you rotate things makes a difference, 1 2 2 1 • We can use this to work out commutation relations for the L’s – It can be done more easily directly • Recall: • Also recall: • We will calculate the following to second order in : • If rotations commuted, both sides would be the identity relation

Calculating the Left Side • To second order in : • Second half is same thing with –

Calculating the Right Side • To second order in : • Second half is same thing with –

Matching the Two Sides • To second order in : • Now match the two sides:

Levi-Civita Symbol • Generalizing, we have • Define the Levi-Civita symbol • Then we write: • We will call any three Hermitian operators J that work this way generalized angular momentum

7 B. Generalized Angular Momentum J 2 and the raising/lowering operators • What can we conclude just from the commutation relations? • If J commutes with the Hamiltonian, than we can simultaneously diagonalize H and one component of J – Normally pick Jz • Define some new operators: • Reverse these if we want: • These satisfy the following properties – Proof by homework problem

Eigenstates • • Since J 2 commutes with Jz, we can diagonalize them simultaneously We will (arbitrarily for now) choose an odd way to write the eigenvalues Note that j and m are dimensionless Note that J 2 has positive eigenvalues – We can choose j to be non-negative • We can let J act on any state |j, m to produce a new state J |j, m : • This new state must be proportional to:

Eigenstates (2) • To find proportionality, consider • This expression must not be negative: • When it is positive, then we have – Choose the phase positive • Conclusion: given a state |j, m , we can produce a series of other states • Problem: if you raise or lower enough times, you eventually get |m| > j • Resolution: You must have:

Summary • Eigenstates look like • The values of m are – There are 2 j + 1 of them • Since 2 j+1 is an integer: We can use these expressions to write out J’s as matrices of size (2 j + 1): • First, pick an order for your eigenstates, traditionally • The matrix Jz is trivial to write down, and is diagonal • The matrix J+ is a little harder, and is just above the diagonal • You then get J- = J+† and can find Jx and Jy

Sample Problem • Basis states • Jz is diagonal: • J+ just above the diagonal: Write out the matrix form for J for j = 1

Sample Problem (2) Write out the matrix form for J for j = 1 • Now work out Jx and Jy: • As a check, find J 2

Special Cases and Pauli Matrices • The matrices for j = 0 are really simple: – We sometimes call this the scalar representation The j = ½ is called the spinor representation, and is important • There are only two states • Often these states abbreviated • The corresponding 2 2 matrices are written in terms of the Pauli matrices • The Pauli matrices are given by: • Useful formulas:

7 C. Spherically Symmetric Problems Spherical Coordinates • Consider this Hamiltonian: • All components of L commute with H, because they commute with R 2 • It makes sense to choose eigenstates of H, L 2 and Lz • It seems sensible to switch to spherical coordinates: • We write Schrödinger’s equation in spherical coordinates

L in Spherical coordinates (1) • We need to write L in spherical coordinates • Start by writing angular derivatives out: • It’s not hard to get Lz from these equations:

L in Spherical coordinates (2) • Now it’s time to get clever: consider • And we get clever once more:

Other Operators in Spherical coordinates • It will help to get the raising and lowering operators: • And we need L 2: • Compare to Schrödinger:

Solving Spherically Symmetric Problems: • Rewrite Schrödinger’s equation: • Our eigenstates will be • The angular properties are governed by l and m • This suggests factoring into angular and radial parts: • Substitute into Schrodinger: • Cancel Y:

The Problem Divided: • It remains to find and normalize R and Y • Note that Y problem is independent of the potential V • Note that the radial problem is a 1 D problem – Easily solved numerically • Normalization: • Split this up how you want, but normally:

7 D. The Spherical Harmonics Dependence on , and m restrictions • We will call our angular functions spherical harmonics and label them • We previously found: • For general angular momentum we know: • We can easily determine the dependence of the spherical harmonics • Also, recall that = 0 is the same as = 2 • It follows that m (and therefore l) is an integer

Finding one Spherical Harmonic: • We previously found: • For general angular momentum: • If we lower m = – l, we must get zero: • Normalize it:

Finding All Spherical Harmonics: • To get the others, just raise this repeatedly: • Sane people, or those who wish to remain so, do not use this formula • Many sources list them – P. 124 for l = 0 to 4 • Computer programs can calculate them for you – Hydrogen on my website

Properties of Spherical Harmonics: • They are eigenstates of L 2 and Lz • They are orthonormal: • They are complete; any angular function can be written in terms of them: • This helps us write the completion relation

More Properties of Spherical Harmonics: • Recall: parity commutes with L • It follows that • Hence when you let parity act, you must be getting essentially the same state • • Recall: L 2 is real but Lz is pure imaginary Take the complex conjugate of our relations above: This implies It works out to

The Spherical Harmonics

7 E. The Hydrogen Atom Changing Operators • Hamiltonian for hydrogen (SI units): • These operators have commutators: • Classically, what we do: – Total momentum is conserved – Center of mass moves uniformly – Work in terms of relative position • Quantum mechanically: Let’s try • Find commutation operators for these – Proof by homework problem • Find the new Hamiltonian – Proof by homework problem

Reducing the problem: 6 D to 3 D • Note that for actual hydrogen, is essentially the electron mass • Split the Hamiltonian into two pieces • These two pieces have nothing to do with each other – It is essentially two problems • Hcm is basically a free particle of mass M, – It is trivial to solve • The remaining problem is effectively a single particle of mass in a spherically symmetric potential

Reducing the problem: 3 D to 1 D • Because the problem is spherically symmetric, we will have states • These will have wave functions • The radial wave function will satisfy: • Note that m does not appear in this equation, so R won’t depend on it • We will focus on bound states E < 0

The Radial Equation: For r Large and Small Let’s try to approximate behavior at r = 0 and r = : • Large r: keep dominant terms, ignore those with negative powers of r: • • • Define a such that: Then we have Want convergent Now, guess that for small r we have Substitute in, keeping smallest powers of r • Want it convergent

The Radial Equation: Removing Asymptotic • Factor out the expected asymptotic behavior: – This is just a definition of f(r) • Substitute in, multiply by 2 / 2 • Define the Bohr radius:

The Radial Equation: Taylor Expansion • Write f as a power series around the origin – Recall that at small r it goes like rl • Substitute in • Gather like powers of r: • On right side, replace i i – 1 • On left side, first term vanishes • These must be identical expressions, so:

Are We Done? • It looks like we have a solution for any E: – Pick fl to be anything – Deduce the rest by recursion • Now just normalize everything • Problem: No guarantee it is normalizable • Study the behavior at large i: • Only way to avoid this catastrophe is to make sure some f vanishes, say fn

Summarizing Everything • Because the exponential beats the polynomial, these functions are now all normalizable – Arbitrarily pick fl > 0 • Online “Hydrogen” or p. 124 • Note that n > l, n is positive integer • Include the angular wave functions • Restrictions on the quantum numbers: • Another way of writing the energy: • For an electron orbiting a nucleus, is almost exactly the electron mass, c 2 = 511 ke. V

Radial Wave Functions

Sample Problem What is the expectation value for R for a hydrogen atom in the state |n, l, m = |4, 2, -1 ? • The spherical harmonics are orthonormal over angles > integrate(radial(4, 2)^2*r^3, r=0. . infinity); 1

Degeneracy and Other Issues Note energy depends only on n, not l or m • Not on m because states related by rotation • Not on l is an accident – accidental degeneracy How many states with the same energy En? • 2 l + 1 values of m • l runs from 0 to n – 1 • Later we will learn about spin, and realize there actually twice as many states Are our results truly exact? • We did include nuclear recoil, the fact that the nucleus has finite mass • Relativistic effects – Small for hydrogen, can show v/c ~ ~ 1/137 • Finite nuclear size – Nucleus is 104 to 105 times smaller – Very small effect • Nuclear magnetic field interacting with the electron

7 E. Hydrogen-Like Atoms Other Nuclei Can we apply our formulas to any other systems? • Other atoms if they have only one electron in them • The charge on the nucleus multiplies potential by Z: • Reduced mass essentially still the electron mass • Just replace e 2 by e 2 Z • Atom gets smaller – But still much larger than the nucleus • Relativistic effects get bigger – Now v/c ~ Z

Bizarre “atoms” We can replace the nucleus or the electron with other things Anti-muon plus electron • Anti-muon has same charge as proton, and much more mass than electron • Essentially identical with hydrogen Positronium = anti-electron (positron) plus electron • Same charge as proton • Positron’s mass = electron’s mass • Reduced mass and energy states reduced by half Nucleus plus muon • Muon 207 times heavier than electron • Atom is 207 times smaller • Even inside a complex atom, muon sees essentially bare nucleus • Atom small enough that for large Z, muon is partly inside nucleus Anti-hydrogen = anti-proton plus anti-electron • Identical to hydrogen
 Angular momentum commutation
Angular momentum commutation Theorem of angular momentum
Theorem of angular momentum Commutation relation in quantum mechanics
Commutation relation in quantum mechanics Commutation function
Commutation function How is leave encashment calculated
How is leave encashment calculated Résumé transistor bipolaire
Résumé transistor bipolaire Commutation relation in quantum mechanics
Commutation relation in quantum mechanics Faclf
Faclf Commutation relation in quantum mechanics
Commutation relation in quantum mechanics Scr forced commutation
Scr forced commutation Larmor frequency equation
Larmor frequency equation Circular motion momentum
Circular motion momentum Rolling torque and angular momentum
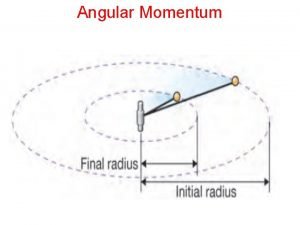
Rolling torque and angular momentum Angular momentum of orbit
Angular momentum of orbit Angular momentum vector
Angular momentum vector Boundary condition for a particle on a ring is
Boundary condition for a particle on a ring is Torque direction right hand rule
Torque direction right hand rule Law of conservation of angular momentum
Law of conservation of angular momentum How to calculate net torque on a wheel
How to calculate net torque on a wheel Angular momentum is vector product of
Angular momentum is vector product of Angular momentum
Angular momentum Whats angular momentum
Whats angular momentum Angular momentum in classical mechanics
Angular momentum in classical mechanics Torque angular velocity
Torque angular velocity Orbital angular momentum
Orbital angular momentum Rolling torque and angular momentum
Rolling torque and angular momentum Addition of three angular momenta
Addition of three angular momenta Angular momentum
Angular momentum Conservation of linear momentum
Conservation of linear momentum Orbital angular momentum
Orbital angular momentum Symbol for rotational inertia
Symbol for rotational inertia Angular momentum operators
Angular momentum operators Neutron degeneracy pressure
Neutron degeneracy pressure Rolling torque and angular momentum
Rolling torque and angular momentum Angular momentum quantum number
Angular momentum quantum number Quantity of angular motion possessed by a body
Quantity of angular motion possessed by a body Angular momentum of a rigid body
Angular momentum of a rigid body @ebbiya
@ebbiya