CSCI 3130 Formal languages and automata theory Tutorial

CSCI 3130: Formal languages and automata theory Tutorial 1 Lee Chin Ho

About me • Name: Chin • Office: SHB 117 • Office hour: Tuesday 11: 00 – 12: 00 • Homework 1 is due on next Thursday

Finite Automata • Finite Automata 1. Q - States 2. S - Alphabets 3. d - Transitions 4. q 0 - Initial state 5. F - Final state(s) / Accepting state(s)

Deterministic Finite Automata • There must be a transition corresponding to each alphabet at each state

Nondeterministic Finite Automata • Can be at multiple states at the same time • Can go to multiple states on one alphabet • May have no transitions on an alphabet (die)

Regular Expression • The symbols Æ and are regular expressions • Every a in S is a regular expression • If R and S are regular expressions, so are R+S, RS and R* • Remember for R*, * could be 0

Regular Languages • Languages that can be represented by a DFA / NFA / RE • DFA = NFA = RE • When asked if a language L is regular, represent L using a DFA / NFA / RE

Checklist 1. Always pay attention to S 2. For DFA, out degree of each state must be equal |S| e. g. S = {0, 1, 2}, L = {w: w begins with 01} 3. For NFA, pay attention to -transitions 4. Remember to specify the initial state 5. Make sure you have considered the input e. g. L = {w: w contains even number of 01}

Example in Lecture 1. q 2 is a “die” state 2. After a 1 has appeared, any 0 appears afterwards will die 3. 0*1* 0 q 0 1 1 q 1 0, 1 0 q 2 S = {0, 1}

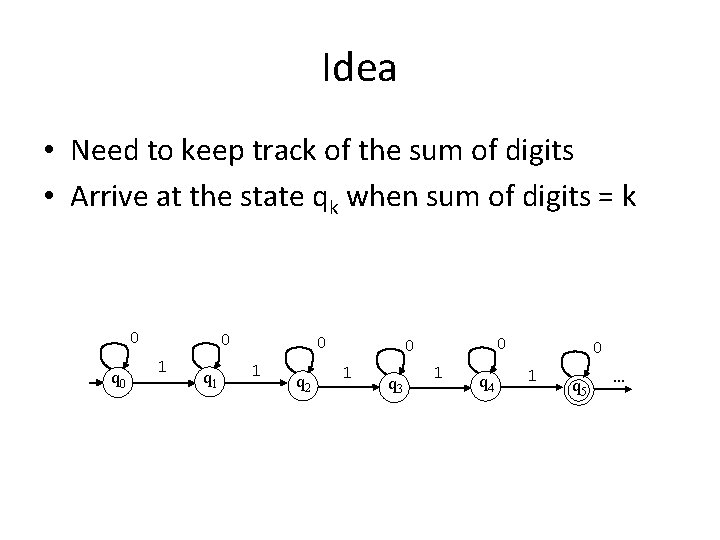
Exercise S = {0, 1} L = {w: w is non-empty and the sum of the digits in w is divisible by 5}

Idea • Need to keep track of the sum of digits • Arrive at the state qk when sum of digits = k 0 q 0 0 1 q 1 0 1 q 2 0 0 1 q 3 1 q 4 0 1 q 5 …

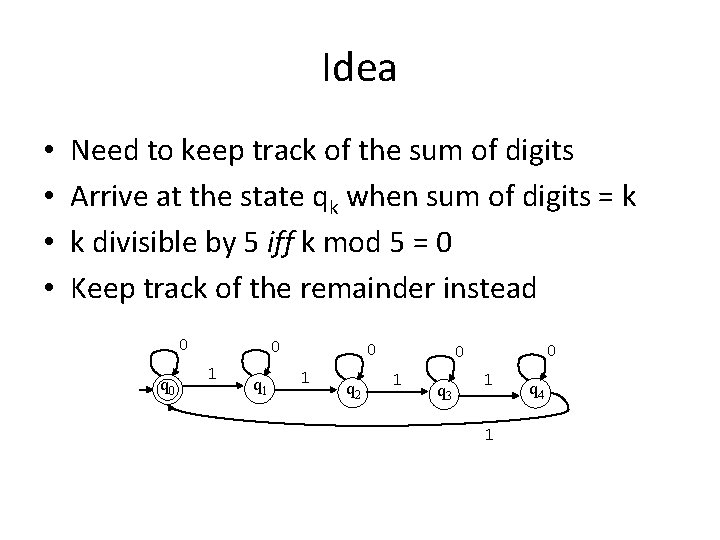
Idea • • Need to keep track of the sum of digits Arrive at the state qk when sum of digits = k k divisible by 5 iff k mod 5 = 0 Keep track of the remainder instead 0 q 0 0 1 q 1 0 1 q 2 0 0 1 q 3 1 1 q 4

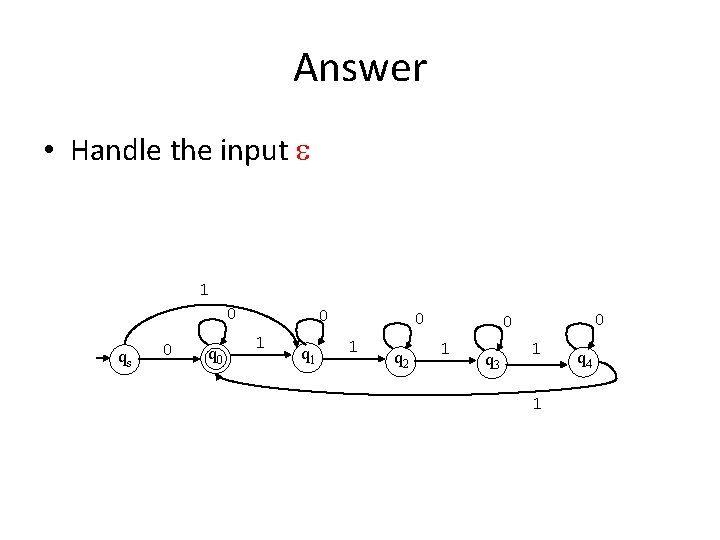
Answer • Handle the input 1 0 qs 0 q 0 0 1 q 1 0 1 q 2 0 0 1 q 3 1 1 q 4

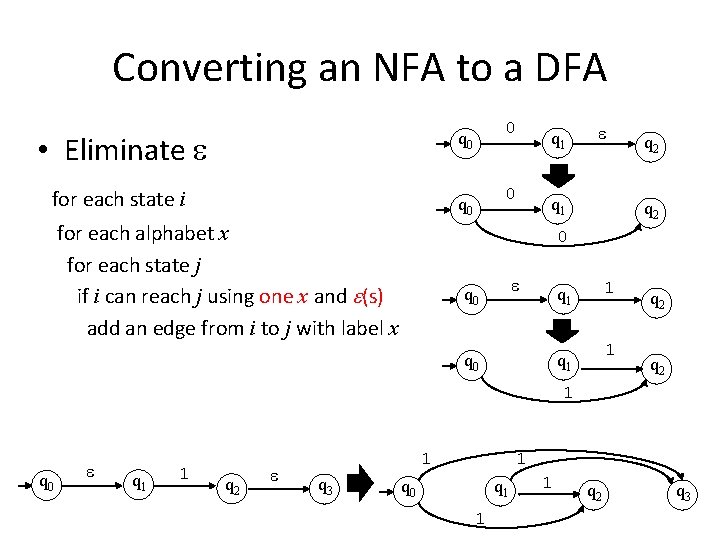
Converting an NFA to a DFA • Eliminate q 0 for each state i q 0 for each alphabet x for each state j if i can reach j using one x and (s) add an edge from i to j with label x 0 0 q 1 q 2 0 q 0 1 q 1 q 2 1 q 0 q 1 1 q 2 1 q 3 1 q 0 q 1 1 1 q 2 q 3

Converting an NFA to a DFA • Eliminate • Remember to consider the case when the initial state can reach accepting states on (s) q 0 q 1 1 1 q 2

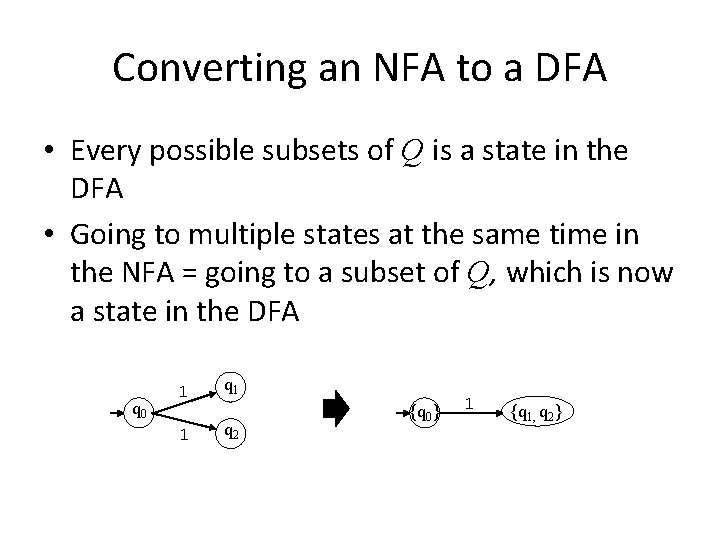
Converting an NFA to a DFA • Every possible subsets of Q is a state in the DFA • Going to multiple states at the same time in the NFA = going to a subset of Q, which is now a state in the DFA q 0 1 q 1 1 q 2 {q 0} 1 {q 1, q 2}

Converting an NFA to a DFA • Empty set ∅ = die S S ∅

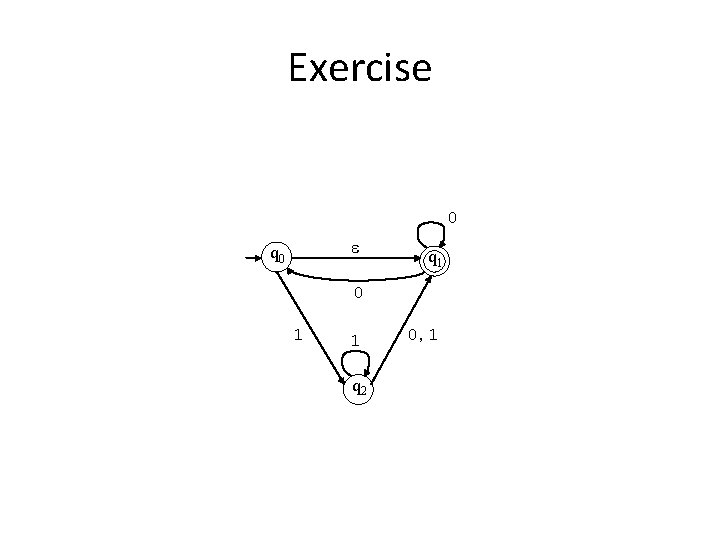
Exercise 0 q 0 q 1 0 1 1 q 2 0, 1

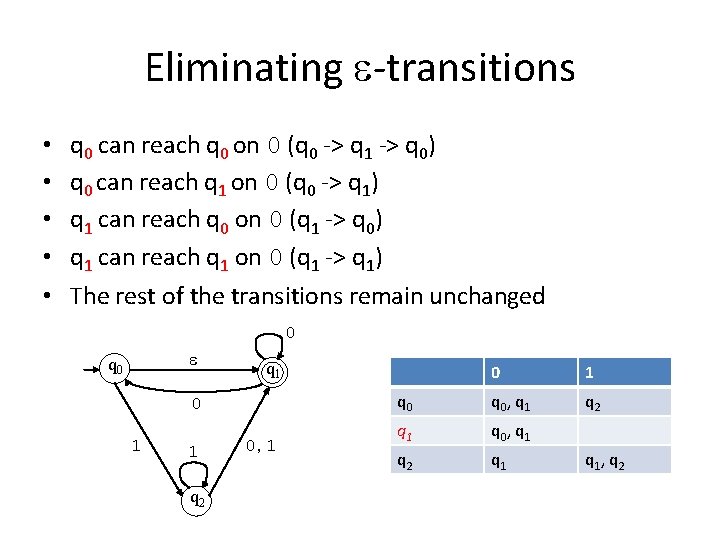
Eliminating -transitions • • • q 0 can reach q 0 on 0 (q 0 -> q 1 -> q 0) q 0 can reach q 1 on 0 (q 0 -> q 1) q 1 can reach q 0 on 0 (q 1 -> q 0) q 1 can reach q 1 on 0 (q 1 -> q 1) The rest of the transitions remain unchanged 0 q 0 q 1 0 1 1 q 2 0, 1 0 1 q 0, q 1 q 2 q 1, q 2

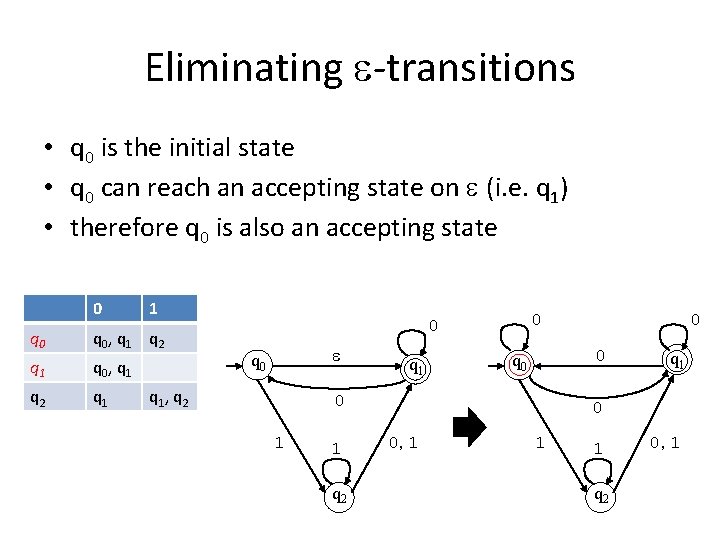
Eliminating -transitions • q 0 is the initial state • q 0 can reach an accepting state on (i. e. q 1) • therefore q 0 is also an accepting state 0 1 q 0, q 1 q 2 q 1 0 0 q 0 q 1, q 2 q 1 0 q 0 0 1 1 q 2 0 q 1 0 0, 1 1 1 q 2 0, 1

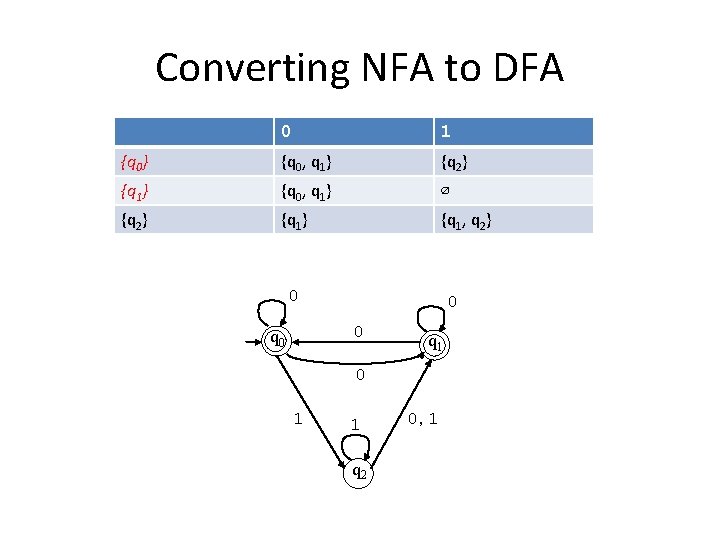
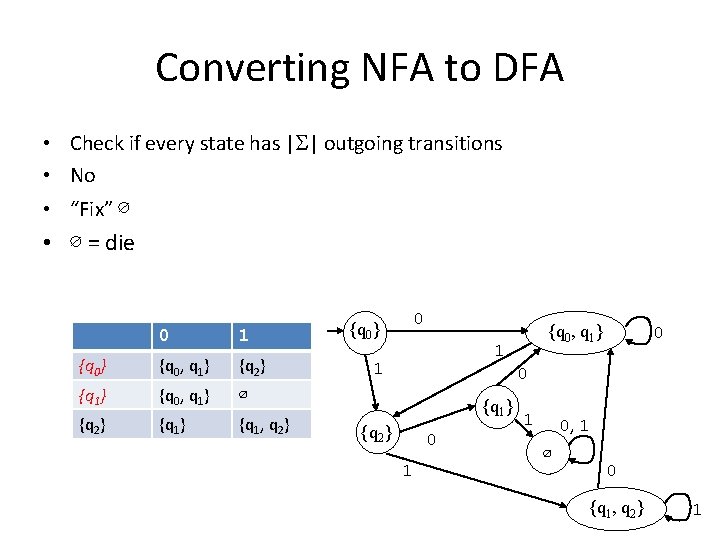
Converting NFA to DFA 0 1 {q 0} {q 0, q 1} {q 2} {q 1} {q 0, q 1} ∅ {q 2} {q 1, q 2} 0 0 0 q 1 0 1 1 q 2 0, 1

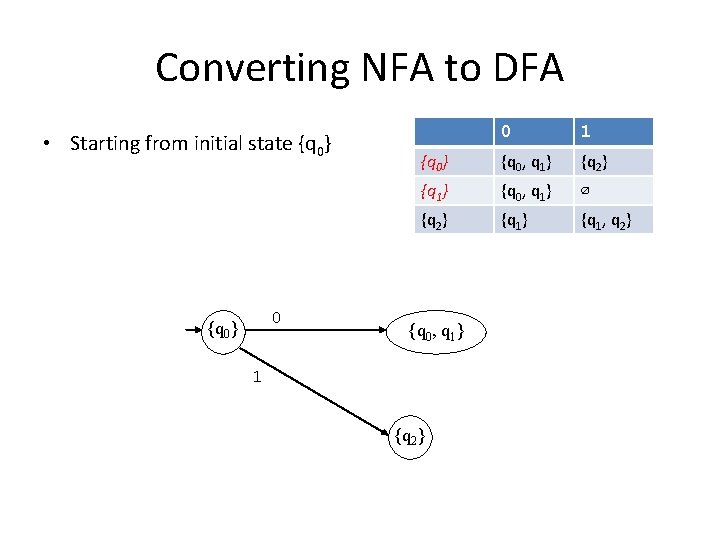
Converting NFA to DFA • Starting from initial state {q 0} 0 1 {q 0} {q 0, q 1} {q 2} {q 1} {q 0, q 1} ∅ {q 2} {q 1, q 2} {q 0, q 1} 1 {q 2}

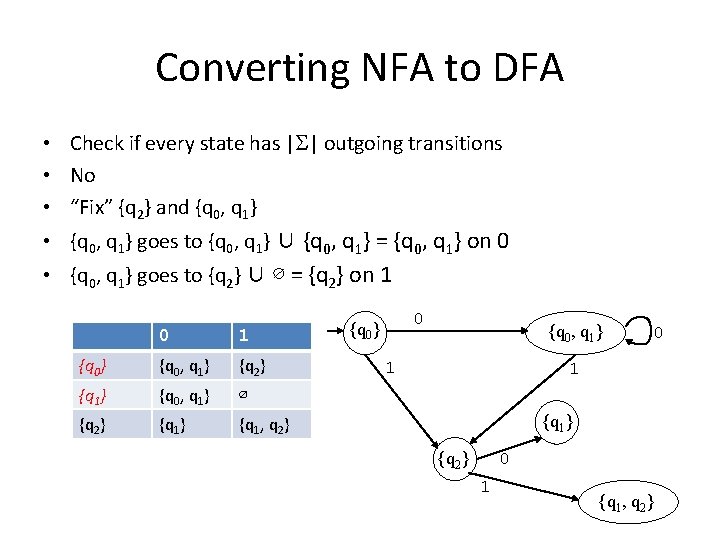
Converting NFA to DFA • Check if every state has |S| outgoing transitions • No • “Fix” {q 2} and {q 0, q 1} • {q 0, q 1} goes to {q 0, q 1} ∪ {q 0, q 1} = {q 0, q 1} on 0 • {q 0, q 1} goes to {q 2} ∪ ∅ = {q 2} on 1 0 1 {q 0} {q 0, q 1} {q 2} {q 1} {q 0, q 1} ∅ {q 2} {q 1, q 2} 0 {q 0} {q 0, q 1} 1 0 1 {q 1} {q 2} 0 1 {q 1, q 2}

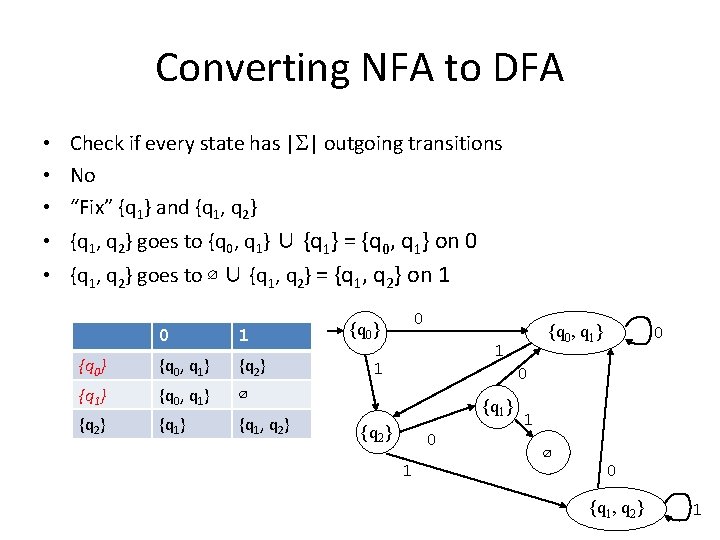
Converting NFA to DFA • Check if every state has |S| outgoing transitions • No • “Fix” {q 1} and {q 1, q 2} • {q 1, q 2} goes to {q 0, q 1} ∪ {q 1} = {q 0, q 1} on 0 • {q 1, q 2} goes to ∅ ∪ {q 1, q 2} = {q 1, q 2} on 1 0 1 {q 0} {q 0, q 1} {q 2} {q 1} {q 0, q 1} ∅ {q 2} {q 1, q 2} 0 {q 0} {q 0, q 1} 1 1 0 0 {q 1} {q 2} 0 1 1 ∅ 0 {q 1, q 2} 1

Converting NFA to DFA • Check if every state has |S| outgoing transitions • No • “Fix” ∅ • ∅ = die 0 1 {q 0} {q 0, q 1} {q 2} {q 1} {q 0, q 1} ∅ {q 2} {q 1, q 2} 0 {q 0} {q 0, q 1} 1 1 0 0 {q 1} {q 2} 0 1 1 0, 1 ∅ 0 {q 1, q 2} 1

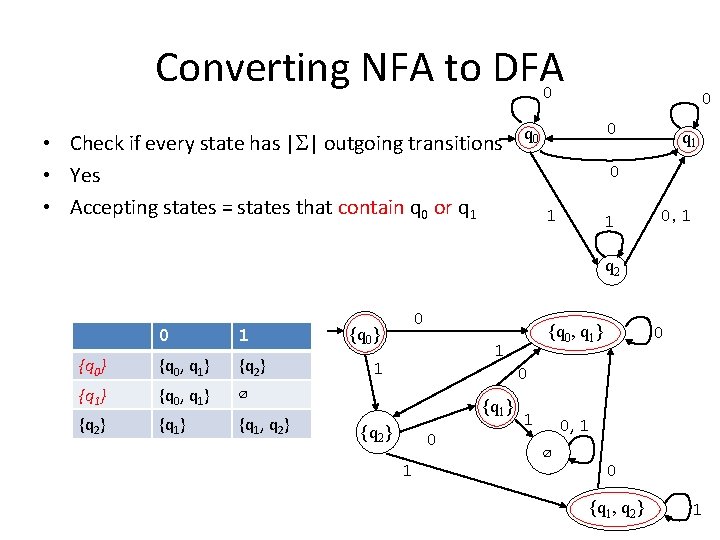
Converting NFA to DFA 0 • Check if every state has |S| outgoing transitions • Yes • Accepting states = states that contain q 0 or q 1 0 0 q 1 0 1 1 0, 1 q 2 0 1 {q 0} {q 0, q 1} {q 2} {q 1} {q 0, q 1} ∅ {q 2} {q 1, q 2} 0 {q 0} {q 0, q 1} 1 1 0 0 {q 1} {q 2} 0 1 1 0, 1 ∅ 0 {q 1, q 2} 1

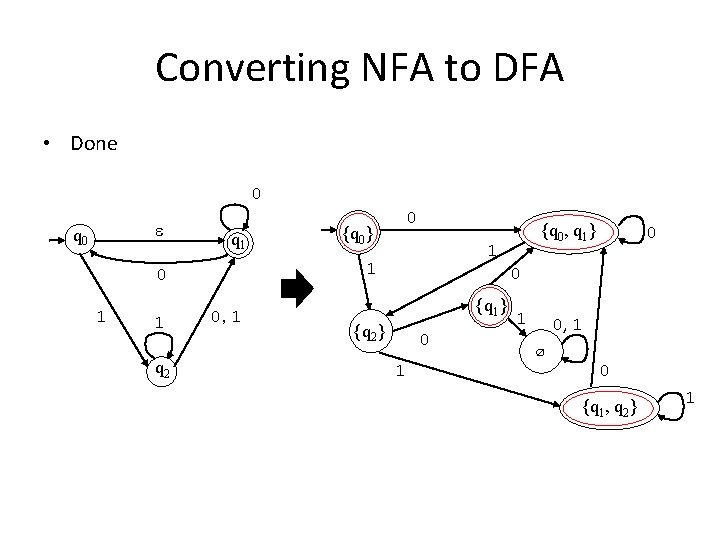
Converting NFA to DFA • Done 0 q 0 q 1 1 q 2 {q 0} 0, 1 {q 0, q 1} 1 1 0 0 0 {q 1} {q 2} 0 1 1 0, 1 ∅ 0 {q 1, q 2} 1