CSCI 3130 Formal languages and automata theory Tutorial

CSCI 3130: Formal languages and automata theory Tutorial 9 Chin

Reminder • Homework 5 is due at next Tuesday! • No tutorial next week! : D • This is the last one.

Undecidable problems for CFGs • ALLCFG = {<G>: G is a CFG that generates all strings} • ALLCFG is undecidable • Reduction • ATM = {<M, w>: M is a TM that does not accept w} = {<M, w>: M rejects or loops on input w} • ATM is unrecognizable ⇒ ATM is undecidable • If ALLCFG is decidable then ATM is decidable. • Contradiction.

Undecidable problems for CFGs • ALLCFG = {<G>: G is a CFG that generates all strings} – ALLCFG is undecidable – Suppose it is decidable, then there exists a universal TM H string // if if } H(string <G>) { G is a CFG G generates all strings, return “accept”; G does not generates all strings, return “reject”; • Consider the following TM U (dependent on <M> and w) string U(string <M>, string w){ If M does not accept w, return <G> that generates all strings If M accepts w, return <G> that does not generate all strings } • If we can simulate H(U(<M>, w)), then U decides ATM and so ATM is decidable.

Undecidable problems for CFGs • ALLCFG = {<G>: G is a CFG that generates all strings} – ALLCFG is undecidable • Consider the following TM U (dependent on <M, w>) string U(string <M>, string w){ If M does not accept w, return <G> that generates all strings If M accepts w, return <G> that does not generate all strings } • We construct U as follows instead: string U(string <M>, string w){ If M does not accept w, construct <G> that generates all strings If M accepts w, construct <G> that generates all strings except the computation history of M(w) return H(<G>) } • How to construct <G>? We need to construct <G> so that even if M loops on w, <G> generates all strings.

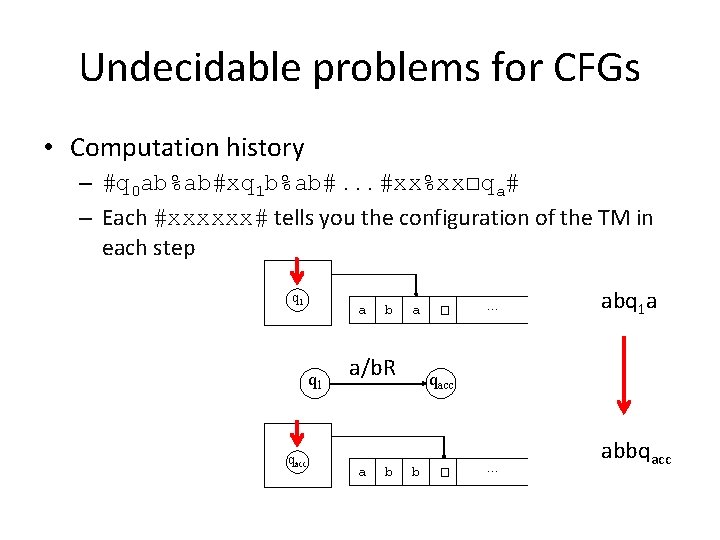
Undecidable problems for CFGs • Computation history – #q 0 ab%ab#xq 1 b%ab#. . . #xx%xx☐qa# – Each #xxxxxx# tells you the configuration of the TM in each step q 1 a q 1 qacc b a a/b. R a b ☐ … abq 1 a qacc b ☐ … abbqacc

Undecidable problems for CFGs • Computation history – Suppose the current configuration is #xbq 1 xab# – What does the next configuration look like? • The head must be one symbol left or one symbol right #xbq 1 xab# – Only these 3 symbols can change • Use this fact to design a PDA that generates the computation history (see lecture notes). • Convert the PDA to <G>.

Undecidable problems for CFGs • PCP = {<T>: T is a collection of tiles that contains a top-bottom match} • PCP is undecidable • AMB = {<G>: G is an ambiguous CFG} • AMB is undecidable • If AMB is decidable, PCP is decidable. Contradiction.

Undecidable problems for CFGs T Terminals: a, b, c, 1, 2, 3 Variables: S, T, B Productions: 1 bab cc S→T|B G (collection of tiles) T → bab. T 1 T → bab 1 B → cc. B 1 B → cc 1 2 (CFG) c ab T → c. T 2 T → c 2 B → ab. B 2 B → ab 2 3 a ab T → a. T 3 T → a 3 B → ab. B 3 B → ab 3

Undecidable problems for CFGs • EQCFG = {<G 1, G 2>: G 1 and G 2 are two CFGs that describe the same language} • Is it decidable?

Undecidable problems for CFGs • EQCFG = {<G 1, G 2>: G 1 and G 2 are two CFGs that descript the same language} • EQCFG is undecidable. • Same idea as EQTM • If EQCFG is decidable, ALLCFG is also decidable. • Let G 1 to be a CFG that generates all inputs.

Undecidable problems for CFGs • EQCFG = {<G 1, G 2>: G 1 and G 2 are two CFGs that descript the same language} • If EQCFG is decidable, there exists a TM H such that string H(string <G 1>, string <G 2>) { if G 1 and G 2 are equal, return “accept”; if G 1 and G 2 are not equal, return “reject”; } • Let G 1 to be a CFG that generates all inputs. We construct U as follows string U(string <G>) { G 1 : = a CFG that generates all inputs // hardcode return H(G 1, G); } • Given a CFG <G>, U(<G>) returns accept if G generates all strings, rejects if G does not. • Hence ALLCFG is decidable. Contradiction.

Post Correspondence Problem • PCP 1 : PCP over the alphabet S = {1}. – The alphabet of a tile is the set of symbols that appear on the tiles. • Is PCP 1 decidable?

Post Correspondence Problem • PCP 1 : PCP over the alphabet S = {1}. – The alphabet of a tile is the set of symbols that appear on the tiles. • PCP 1 is decidable. 111 1 • • 11 11111 3 – 1 = 2 2 – 5 = -3 Find x, y such that 2 x – 3 y = 0. Easy. If exists two tiles like above, accept. Otherwise reject.

Post Correspondence Problem • PCP 2 : PCP over the alphabet S = {0, 1}. – The alphabet of a tile is the set of symbols that appear on the tiles. • Is PCP 2 decidable?

Post Correspondence Problem • PCP 2 : PCP over the alphabet S = {0, 1}. – The alphabet of a tile is the set of symbols that appear on the tiles. • PCP 2 is undecidable. • If PCP 2 is decidable, then PCP is also decidable. • Represent the alphabet in PCP in binary form.

End • Questions?