Tutorial 03 CSC 3130 Formal Languages and Automata

Tutorial 03 -- CSC 3130 : Formal Languages and Automata Theory Haifeng Wan (hfwan@cse. cuhk. edu. hk) 2009 -09 -27

Outline n Pumping Lemma n DFA Minimization n Context-free Languages

Pigeonhole Principle n Pigeonhole principle n If m objects are put into n containers, where m>n, then at least one container must hold more than one object. n The pigeonhole can be used to prove that certain infinite languages are not regular. n Remind: any finite language is regular.

Pumping Lemma for Regular Languages n Theorem: For every regular language L There exists a number n such that for every string z in L, we can write z = uvw where |uv| ≤ n |v| ≥ 1 For every i ≥ 0, the string u vi w is in L. z … u v … w

Pumping Lemma n What does the Pumping Lemma say? n If an infinite language is regular, it can be defined by a DFA. n The DFA has a finite number m of states. n Since the language is infinite, some strings of the language must have length greater than m. n For a string of length greater than m accepted by the DFA, the walk through the DFA must contain a cycle. n Repeating the cycle an arbitrary number of times must yield another string accepted by the DFA. n Remind: the Pumping Lemma is not sufficient. n It is one way to prove that a given infinite language is not regular, while it cannot be used to prove that a given infinite language is regular.

Outline to Prove by Pumping Lemma n Main idea: prove by contradiction. n Brief outline: n Assume the language L is regular (and thus the Pumping Lemma holds). n Show that repeating the cycle some number of times (“pumping” the cycle) yields a string that is not in L. n Conclude that L is not regular by contradiction. n What can we think about during using Pumping Lemma? n n On choosing the particular string z in L. On choosing the number of times to “pump” the cycle.

Example 1 n Prove that L 3={uu: u in {0, 1}*} is not regular. n Suppose L 3 is regular, there exists n n Choose a string z=0 m 1 with m>n, n Although the decomposition of z into uvw is unknown, uv must consist entirely of 0 s because |uv|≤n. Moreover, |v|≥ 1. Simply choose i=2. Thus uv 2 w will have more 0 s before the first 1 than the second 1, which is not in L 3. Thus L 3 is not regular due to the contradiction. n n

Example 2 n Prove that L={x: x has different numbers of 0 s and 1 s} is not regular. n Trick: n Instead of directly prove this, let’s prove its dual stated language D={x: x has the same number of 0 s and 1 s} is not regular. n Steps: n Remind that we have proven L={0 n 1 n: n≥ 0} is not regular. And L = D n n If L is regular, then D should also be regular. Thus D is not regular according to the contradiction. Neither is L. .

n Take x = 0^n 1^{n! + n}. n Then the adversary splits it as uvw. Let k be the length of the v part. n Now pump it (n!+k)/k times. n Then you get uv^iw = 0^{k((n!+k)/k) + (n- k)}1^{n!+n} = 0^{n! + n}1^{n! + n}

Example n Prove that n n n L 2 ={1 m: m is prime} is not regular. Suppose L 2 is regular, and thus Pumping Lemma holds. Although n is unknown, we can still assume that there is one. Choose a string z=1 m where m is a prime number and |uvw|=m>n+1. Any prefix of z consists entirely of 1 s. Although the decomposition of z into uvw is unknown, it follows that |w|>1 due to |uvw|> n. Moreover, |v|≥ 1. Choose i=|uw|. (Remind |w|>1 and |uw|>1). We have |u vi w|=|uw|+|v||uw|=(1+|v|)|uw|. Because both 1+|v| and |uw| are greater than 1, the product must be a composite number, i. e. , |u vi w| is a composite not a prime number. It is not in L 2. Thus, L 2 is not regular due to the contradiction. Q. E. D.

Outline n Pumping Lemma n DFA Minimization n Context-free grammars (CFG)

DFA Minimization n There is an algorithm to start with any DFA and reduce it to the smallest possible DFA n The algorithm attempts to identify classes of equivalent states n These are states that can be merged together without affecting the answer of the computation

Equivalent and Distinguishable States n Two states q, q’ are equivalent if ^ d(q, w) and ^ For every string w, the states d(q’, w) are either both accepting or both rejecting ^ w) is the state that the machine is in n Here, d(q, if it starts at q and reads the string w n q, q’ are distinguishable if they are not equivalent: For some string w, one of the states d(q, w), d(q’, w) is accepting and the other is rejecting

DFA Minimization Algorithm n Find all pairs of distinguishable states as follows: For any pair of states q, q’: If q is accepting and q’ is rejecting Mark (q, q’) as distinguishable Repeat until nothing is marked: For any pair of states (q, q’): For every alphabet symbol a: If (d(q, a), d(q’, a)) are marked as distinguishable Mark (q, q’) as distinguishable For any pair of states (q, q’): If (q, q’) is not marked as distinguishable Merge q and q’ into a single state

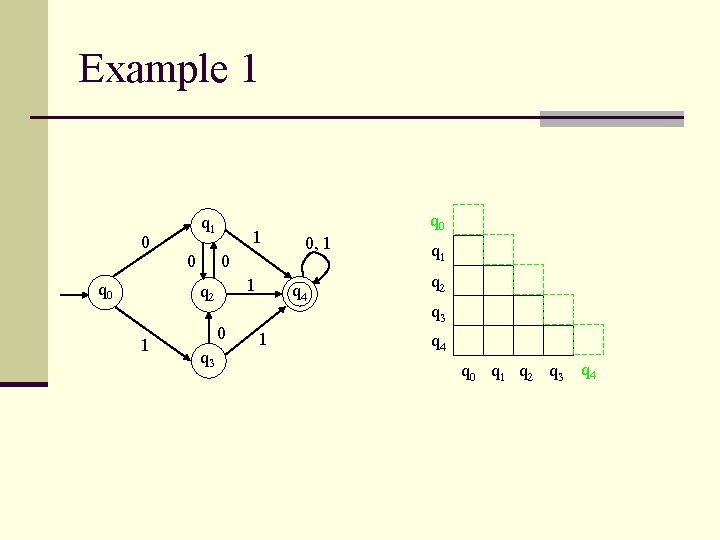
Example 1 0 q 1 0 1 q 2 1 0 q 3 q 0 0, 1 q 4 1 q 2 q 3 q 4 q 0 q 1 q 2 q 3 q 4

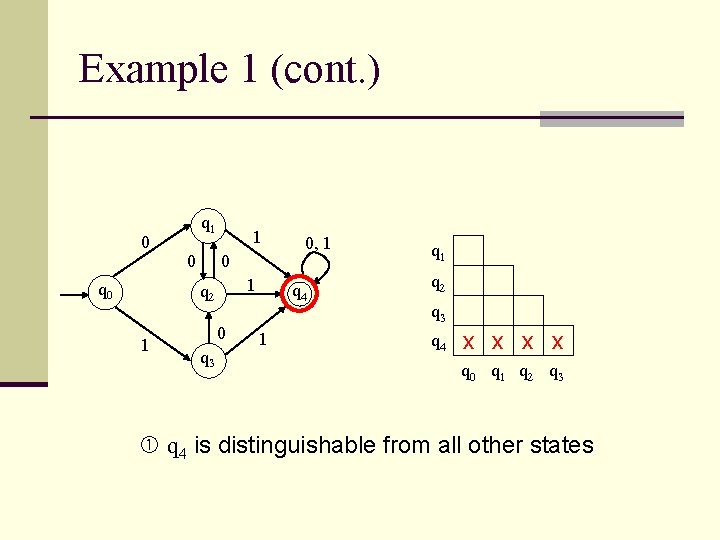
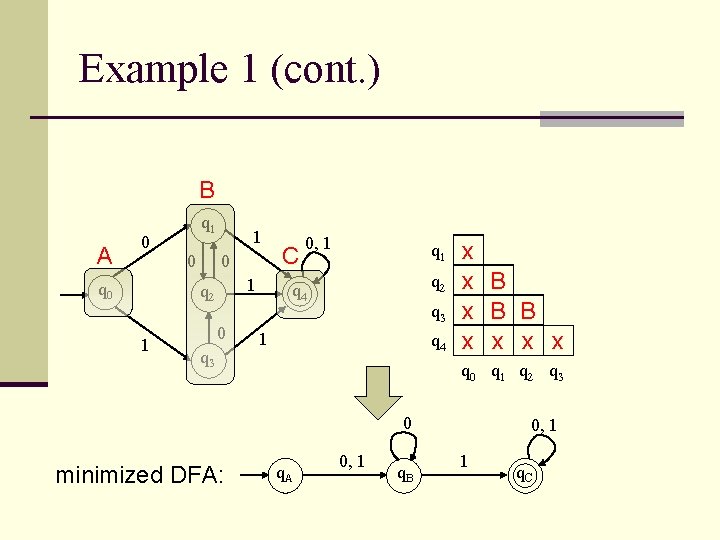
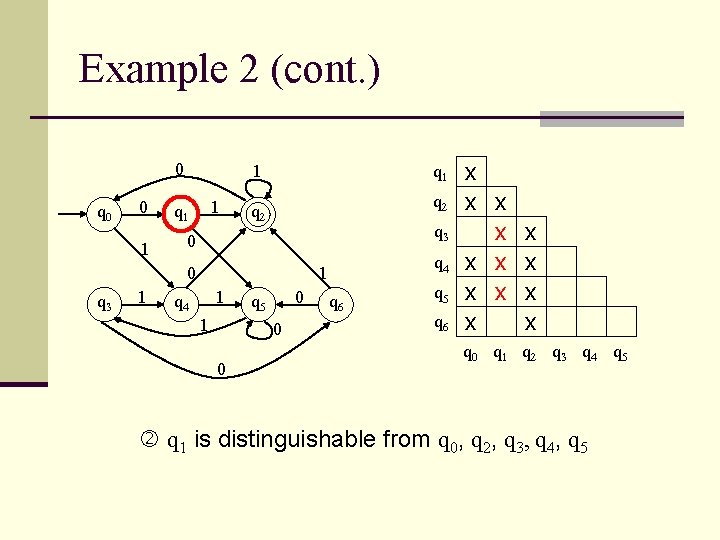
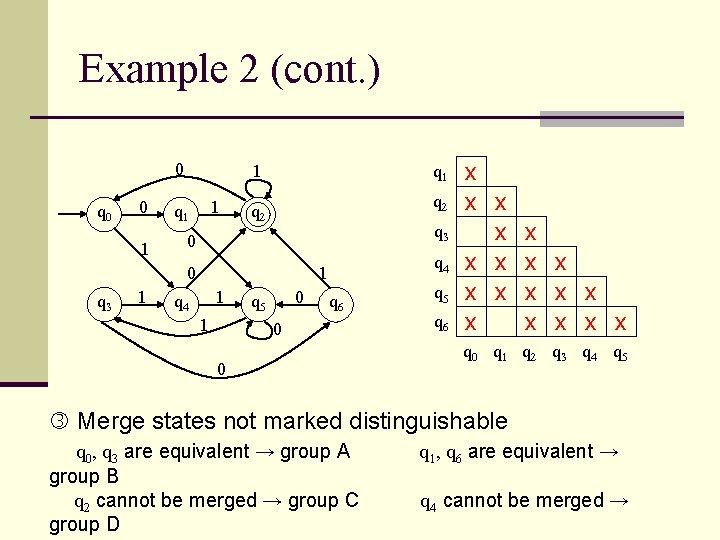
Example 1 (cont. ) 0 q 1 0 1 q 2 1 0 q 3 0, 1 q 4 1 q 2 q 3 q 4 x x q 0 q 1 q 2 q 3 q 4 is distinguishable from all other states

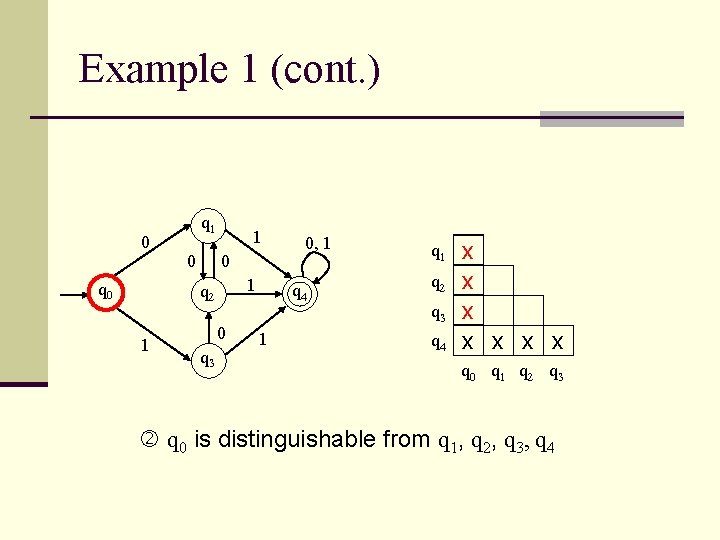
Example 1 (cont. ) 0 q 1 0 1 q 2 1 0 q 3 0, 1 q 4 1 q 2 q 3 q 4 x x x x q 0 q 1 q 2 q 3 q 0 is distinguishable from q 1, q 2, q 3, q 4

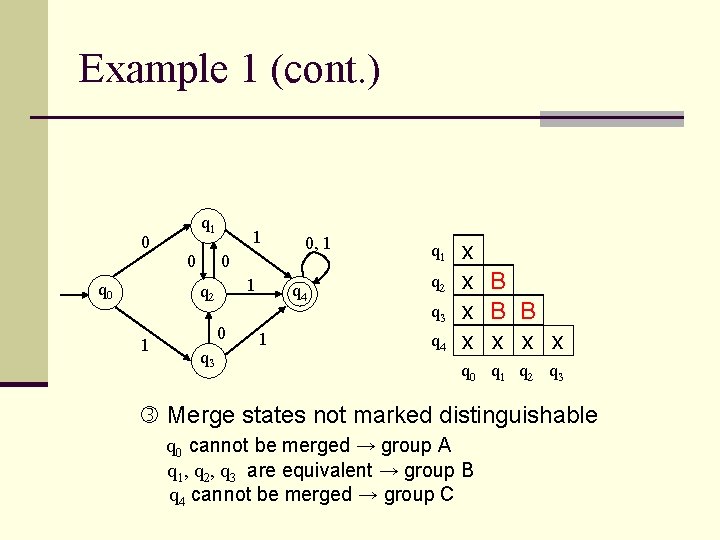
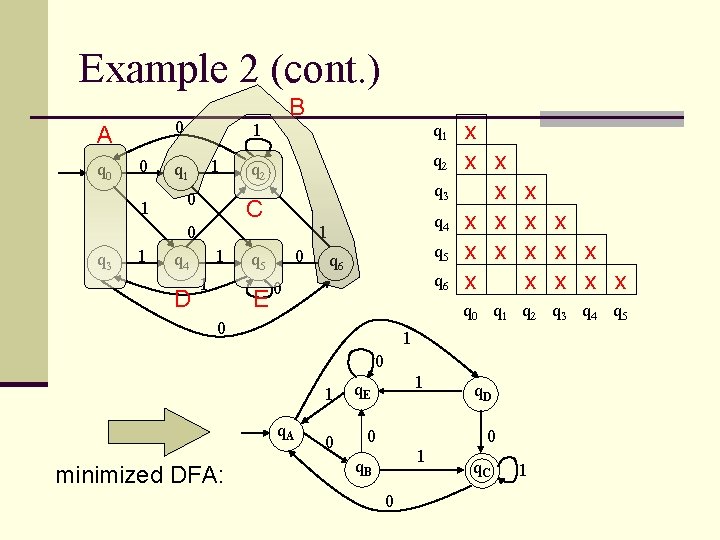
Example 1 (cont. ) 0 q 1 0 1 q 2 1 0 q 3 0, 1 q 4 1 q 2 q 3 q 4 x x B B x x q 0 q 1 q 2 q 3 Merge states not marked distinguishable q 0 cannot be merged → group A q 1, q 2, q 3 are equivalent → group B q 4 cannot be merged → group C

Example 1 (cont. ) B A 0 q 1 0 1 q 2 1 0 q 3 C 0, 1 q 2 q 4 q 3 1 q 4 x x B B x x q 0 q 1 q 2 q 3 0 minimized DFA: q. A 0, 1 q. B 0, 1 1 q. C

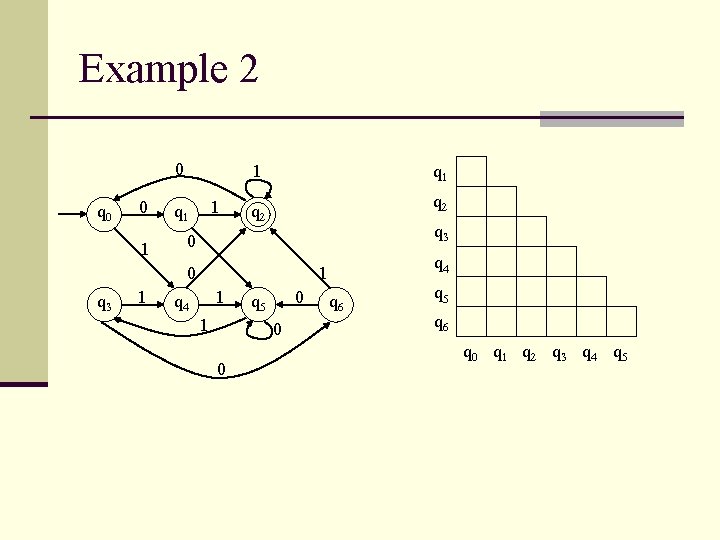
Example 2 0 q 0 0 1 1 1 q 1 q 2 q 3 0 0 q 3 1 q 4 1 0 q 5 0 0 q 6 q 5 q 6 q 0 q 1 q 2 q 3 q 4 q 5

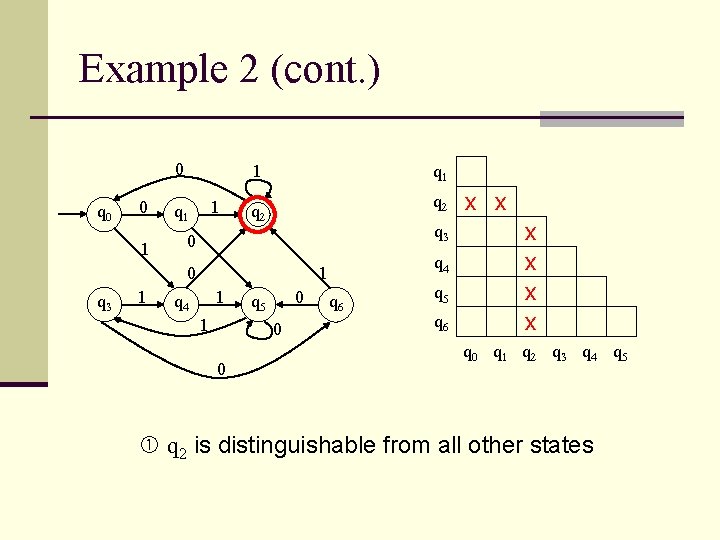
Example 2 (cont. ) 0 q 0 0 1 1 1 q 1 q 2 q 3 0 0 q 3 1 q 4 1 0 q 5 0 0 q 6 q 5 q 6 x x x q 0 q 1 q 2 q 3 q 4 q 5 q 2 is distinguishable from all other states

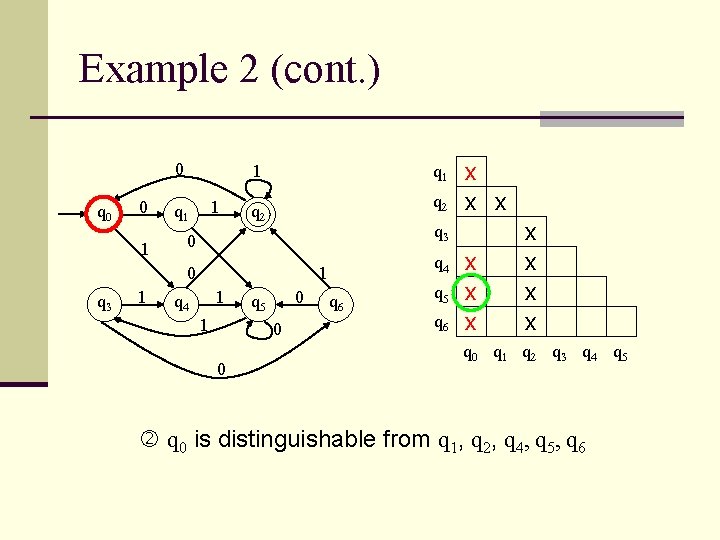
Example 2 (cont. ) 0 q 0 0 1 1 1 q 1 q 2 q 3 0 0 q 3 1 q 4 1 0 q 5 0 0 x x x q 6 q 5 q 6 x x x x q 0 q 1 q 2 q 3 q 4 q 5 q 0 is distinguishable from q 1, q 2, q 4, q 5, q 6

Example 2 (cont. ) 0 q 0 0 1 1 1 q 1 q 2 q 3 0 0 q 3 1 q 4 1 0 q 5 0 0 q 6 q 5 q 6 x x x x q 0 q 1 q 2 q 3 q 4 q 5 q 1 is distinguishable from q 0, q 2, q 3, q 4, q 5

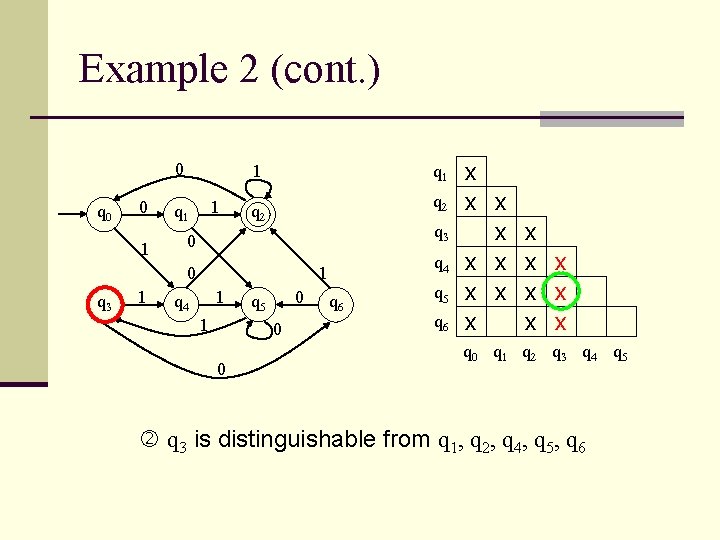
Example 2 (cont. ) 0 q 0 0 1 1 1 q 1 q 2 q 3 0 0 q 3 1 q 4 1 0 q 5 0 0 q 6 q 5 q 6 x x x x q 0 q 1 q 2 q 3 q 4 q 5 q 3 is distinguishable from q 1, q 2, q 4, q 5, q 6

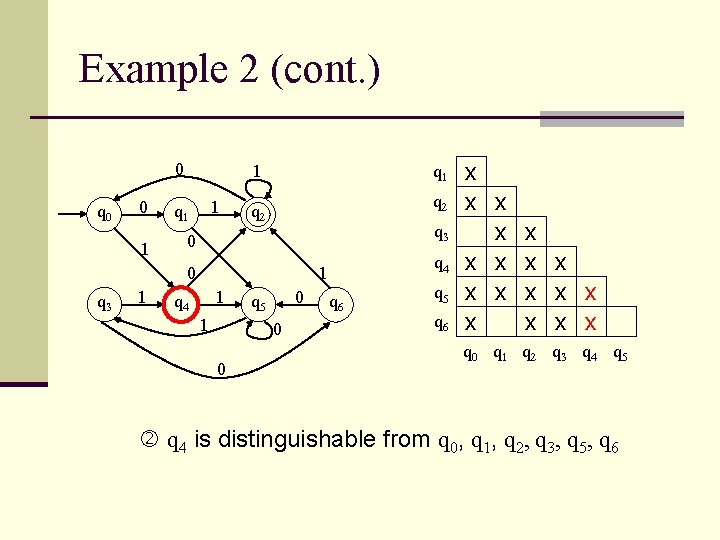
Example 2 (cont. ) 0 q 0 0 1 1 1 q 1 q 2 q 3 0 0 q 3 1 q 4 1 0 q 5 0 0 q 6 q 5 q 6 x x x x x q 0 q 1 q 2 q 3 q 4 q 5 q 4 is distinguishable from q 0, q 1, q 2, q 3, q 5, q 6

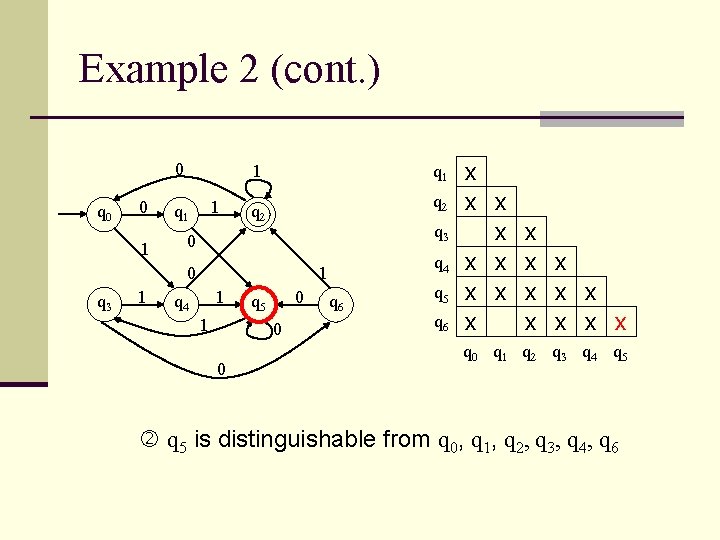
Example 2 (cont. ) 0 q 0 0 1 1 1 q 1 q 2 q 3 0 0 q 3 1 q 4 1 0 q 5 0 0 q 6 q 5 q 6 x x x x x q 0 q 1 q 2 q 3 q 4 q 5 is distinguishable from q 0, q 1, q 2, q 3, q 4, q 6

Example 2 (cont. ) 0 q 0 0 1 1 1 q 1 q 2 q 3 0 0 q 3 1 q 4 1 0 q 5 q 6 0 0 q 5 q 6 x x x x x q 0 q 1 q 2 q 3 q 4 q 5 Merge states not marked distinguishable q 0, q 3 are equivalent → group A group B q 2 cannot be merged → group C group D q 1, q 6 are equivalent → q 4 cannot be merged →

Example 2 (cont. ) 0 A q 0 0 1 1 1 q 1 0 1 1 q 4 D 1 q 2 q 3 C 0 q 3 B 0 q 5 E q 4 1 q 5 q 6 0 x x x x x q 0 q 1 q 2 q 3 q 4 q 5 0 1 0 q. A minimized DFA: 1 q. E 0 0 1 q. D 0 1 q. B 0 q. C 1

Outline n Pumping Lemma n DFA Minimization n Context-free Languages

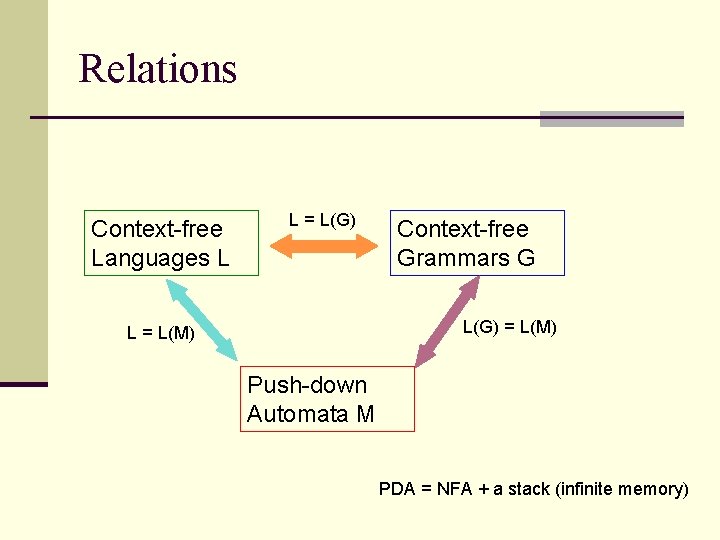
Relations Context-free Languages L L = L(G) Context-free Grammars G L(G) = L(M) L = L(M) Push-down Automata M PDA = NFA + a stack (infinite memory)

Example (I) n Given the following CFG S X | Y X a. Xb | a. X Y a. Yb | Yb n (1) L(G) = ? Σ={a, b} | a | b

Example (I) --- solution: L(S) S X|Y X a. Xb | a. X | a Y a. Yb | b Try to write some strings generated by it: S X a. Xb aa. Xbb aaaabb more a’s than b’s S Y a. Ybb aa. Ybbb aabbbb more b’s than a’s Observations: • Start from S, we can enter two States X & Y, and X, Y are “independent”; Ls = Lx U Ly • In X state, always more a are generated; Lx = { aibj; i>j } • In Y state, always more b are generated. Lx = { aibj; i<j } L(S) = { aibj; i≠j }

End of this tutorial! Thanks for coming!

Example (II) n Given the following language: L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, n (1) design a CFG for it; S = {0, 1}

Example (II) -- solution: CFG L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, 1} S = {0, Consider two extreme cases: (a). if j = i, then L 1 = { 0 i 1 j: i=j }; (b). if j = 2 i, then L 2 = { 0 i 1 j: 2 i=j }. S 0 S 1 “red-rule” S ε S 0 S 11 S ε If i ≤ j ≤ 2 i , then randomly choose “redrule” or “blue-rule” in the generation. S 0 S 11 S ε “blue-rule”

Example (II) -- solution: CFG L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, S = {0, 1} Need to verify L = L(G) G= S 0 S 11 S ε 1). L(G) is a subset of L: The “red-rule” and “blue-rule” guarantee that in each derivation, the number of 1 s generated is one or two times larger than that of 0 s. So, L(G) is a subset of L. 2). L is a subset of L(G): For any w = 0 i 1 j, i ≤ j ≤ 2 i, we use “red-rule” (2 i - j) times and then “blue-rule” ( j - i ) times, i. e. , S =*=> 02 i-j. S 12 i-j =*=> 02 i-j 0 j-i. S 12(j-i)12 i-j ==> 0 i 1 j = w