CSCI 3130 Formal languages and automata theory Tutorial






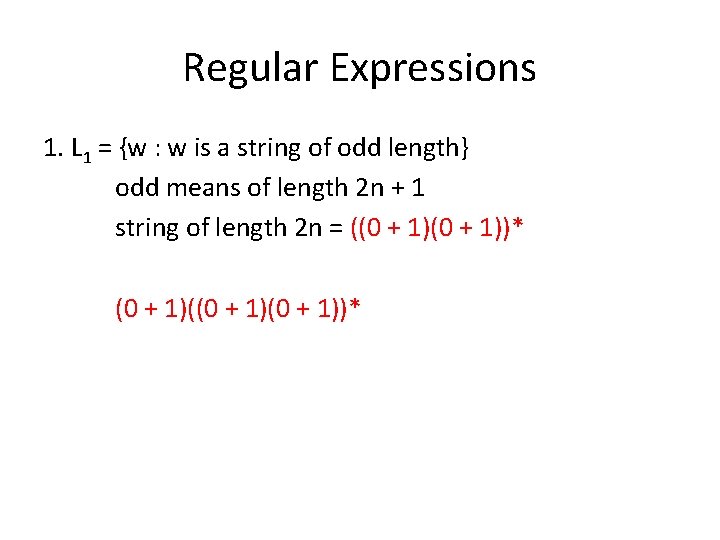




















- Slides: 27

CSCI 3130: Formal languages and automata theory Tutorial 2 Chin

Reminder • Homework 1 is due at 23: 59, today! • Subscribe Moodle for tutorial information • My office hour: 11: 00 – 12: 00, Tuesday

Outline • Regular expression • Closure properties • In this (only this) tutorial. Assume S = {0, 1}.

Regular Expressions • The symbols Æ and e are regular expressions • Every a in S is a regular expression • If R and S are regular expressions, so are R+S, RS and R* • Remember for R*, * could be 0

Regular Expressions • What are their regular expressions? 1. L 1 = {w : w is a string of even length} ((0 + 1))* 2. L 2 = {w : w begins with 0 or ends with 0} 0(0 + 1)* + (0 + 1)*0 3. L 3 = {w : w contains the pattern 01 at least once} (0 + 1)* 01 (0 + 1)*

Regular Expressions • What are their regular expressions? 1. L 1 = {w : w is a string of odd length} 2. L 2 = {w : w begins with 0 or ends with 0 but not both} 3. L 3 = {w : w contains the pattern 01 at least twice} 4. L 4 = {w : w contains less 1 s than 0 s and at most two 0 s}
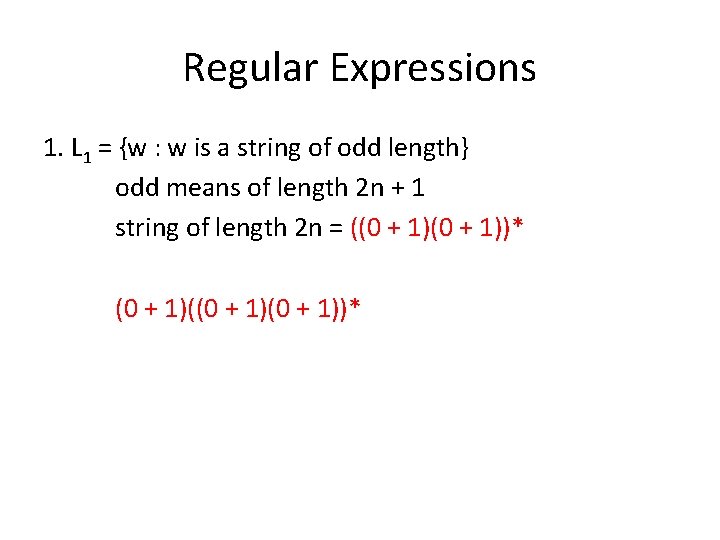
Regular Expressions 1. L 1 = {w : w is a string of odd length} odd means of length 2 n + 1 string of length 2 n = ((0 + 1))* (0 + 1)(0 + 1))*

Regular Expressions 2. L 2 = {w : w begins with 0 or ends with 0 but not both} w must be of length at least 2 Either starts with 0 and ends with 1, or starts with 1 and ends with 0 0(0 + 1)*1 + 1(0 + 1)*0

Regular Expressions 3. L 3 = {w : w contains the pattern 01 at least twice} w must contain 01 twice in the expression can be anything before, after, or between the two 01 s (0 + 1)* 01 (0 + 1)*

Regular Expressions 4. L 4 = {w : w contains less 1 s than 0 s and at most two 0 s} There can be at most two 0 s Enumerate all possible cases: 0, 001, 010, 100 OR them using + 001 + 010 + 100

Regular Expressions • What do these regular expressions represent? 1. 0(0 + 1)*0 + 1(0 + 1)*1 + 0 + 1 2. 1*(011*)* 3. (0*10*10*)* 4. ((0 + 1)1)*

Regular Expression 1. 0(0 + 1)*0 + 1(0 + 1)*1 + 0 + 1 First alphabet must be equal to the last alphabet

Regular Expression 2. 1*(011*)* 011* = start with 0 then followed by at least one 1 (011*)* = start with 0 and every 0 must be followed by at least one 1 1* at the beginning = possibly start with 1 s Every 0 is followed by at least one 1

Regular Expression 3. (0*10*10*)* There are two 1 s inside the brackets 0*10*10* = there can be 0 before, after, or between the two 1 s = there are two 1 s (0*10*10*)* = there are 2 n 1 s All strings that contain even number of 1 s

Regular Expression 4. ((0 + 1)1)* (0 + 1)1 = X 1, X = 0/1 ((0 + 1)1)* = strings of the form X 1 X 1…X 1, X = 0/1 Strings of even length and every even position is 1

Closure Properties • Suppose L and L’ are both regular 1. L is also regular 2. LR is also regular 3. L ∪ L’ is also regular 4. L ∩ L’ is also regular

Closure Properties • Suppose L and L’ are both regular. Then L and L’ are also regular L ∪ L’ is also regular (L ∪ L’) is also regular L ∩ L’ = (L ∩ L’) by De Morgan’s law 4. Hence L ∩ L’ is also regular The construction idea in lecture is also important.

Closure Properties Let L be a language comprising all strings w such that 1. w contains an even number of 1 s, 2. an odd number of 0 s, and 3. no occurrences of the substring 10. Is L regular?

Closure Properties • To show a language L is regular, 1. represent L using a DFA / NFA / RE, or 2. use closure properties

Closure Properties 1. L 1 = {w : w contains an even number of 1 s} regular 2. L 2 = {w : w contains an odd number of 0 s} regular 3. L 3 = {w : w contains the substring 10} regular

Closure Properties Let L be a language comprising all strings w such that 1. w contains an even number of 1 s, 2. an odd number of 0 s 3. no occurrences of the substring 10. Is L regular? L = L 1∩L 2∩L 3. Hence it is regular.

Regular Expression (Extra) • L = {1 ky : y ∈ {0, 1}* and y contains at least k 1 s, k ≥ 1} • What is the regular expression of L?

Regular Expression (Extra) • L = {1 ky : y ∈ {0, 1}* and y contains at least k 1 s, k ≥ 1} 1 k y e. g. 111 0001111 (k = 3) is in L.

Regular Expression (Extra) • L = {1 ky : y ∈ {0, 1}* and y contains at least k 1 s, k ≥ 1} 1 k y • What about 111 00011? • Same as 1 1100011. Hence is in L! • L = Strings that start with 1 and contain at least two 1 s

Non-regular languages • Homework 1 Problem 4 • What happens if we allow nested parans?

Non-regular languages • • Consider the case ((((( ))))) same as L = {(n )n : n ≥ 0} L’ = {0 n 1 n : n ≥ 0} is NOT regular (lecture) • More on non-regular languages next week.

The End • Questions?