THEORY OF COMPUTATION Lecture One Automata Theory 1

THEORY OF COMPUTATION Lecture One: Automata Theory 1

Automaton • With every automaton, a transition function is associated which gives the next state in terms of the current state • The labels on the edges show what happens (in terms of input and output) during the transitions Automata Theory 2

Components of an automaton • Input file : Contains strings of input symbols • Storage unit: consists of an unlimited number of cells, each capable of holding a single symbol from an alphabet • Control unit : can be in any one of a finite number of internal states and can change states in defined manner Automata Theory 3

Some Terms used in automaton theory • Alphabets-Everything in mathematics is based on symbols. This is also true for automata theory. Alphabets are defined as a finite set of symbols. An example of alphabet is a set of decimal numbers ∑={0, 1, 2, 3, 4, 5, 6, 7, 8, 9} • Strings- A string is a finite sequence of symbols selected from some alphabet If ∑ {a, b} is an alphabet then abab is string over alphabet ∑. A string is generally denoted by w. The length of string is denoted by |w| • Empty string is string with zero occurrence of symbols. This string is represented by є Automata Theory 4

Finite Automaton • One of the powerful models of computation which are restricted model of actual computer is called finite automata. These machines are very similar to CPU of a computer. They are restricted model as they lack memory. • Finite automation is called finite because number of possible states and number of letter in alphabet are both finite and automation because the change of state is totally governed by the input. Automata Theory 5

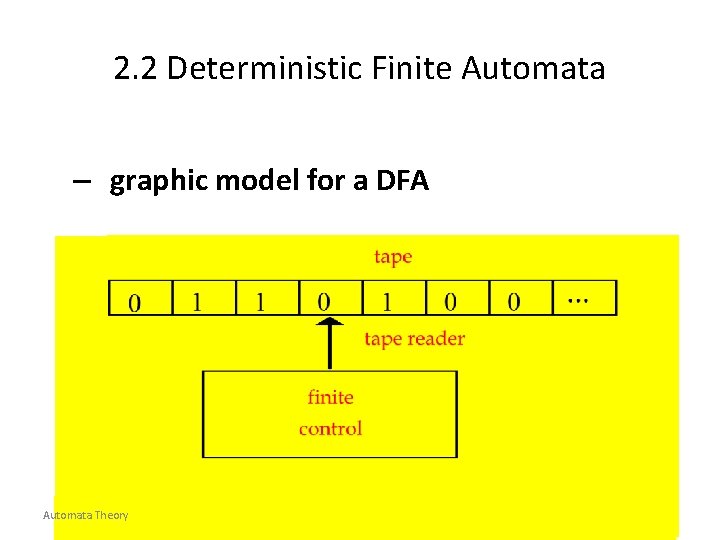
2. 2 Deterministic Finite Automata – graphic model for a DFA Automata Theory 6

Finite Automata FA • Its goal is to act as a recognizer for specific a language/pattern. • Any problem can be presented in form of decidable problem that can be answered by Yes/No. • Hence FA (machine with limited memory) can solve any problem. Automata Theory 7

Deterministic Finite Automata DFA FA = “a 5 -tuple “ (Q, Σ, � , q 0, F) 1. Q: {q 0, q 1, q 2, …} is set of states. 2. Σ: {a, b, …} set of alphabet. 3. � (delta): represents the set of transitions that FA can take between its states. �: Q x Σ→Q Q x Σ to Q, this function: Takes a state and input symbol as arguments. Returns a single state. �: Q x Σ→Q 4. q 0 5. F Automata Theory Q is the start state. Q is the set of final/accepting states. 8

• In transition, DFA cannot use n empty string, and it can be understood as one machine. • A DFA machine can be constructed with every input and output. Automata Theory 9

Transition function � Ø �: Q x Σ→Q Ø Maps from domain of (states, letters) to range Q of states. QxΣ (q 0, a) q 1 (q 2, b) q 2 (q 1, b) Automata Theory q 3 10

How does FA work? 1. Starts from a start state. 2. Loop Reads a sequence of letters 3. Until input string finishes 4. If the current state is a final state then Input string is accepted. 5. Else • Input string is NOT accepted. But how can FA be designed and represented? Automata Theory 11

Transition System FA = “a 5 -tuple “ (Q, Σ, � , q 0, F) 1. Q: {q 0, q 1, q 2, …} is set of states. 2. Σ: {a, b, …} set of alphabet. 3. � (delta): represents the set of transitions that FA can take between its states. �: Q x Σ→Q Q x Σ to Q, this function: Takes a state and input symbol as arguments. Returns a single state. �: Q x Σ→Q 4. q 0 5. F Automata Theory Q is the start state. Q is the set of final/accepting states. 12

Transition System Transition Diagrams Automata Theory Transition Tables 13

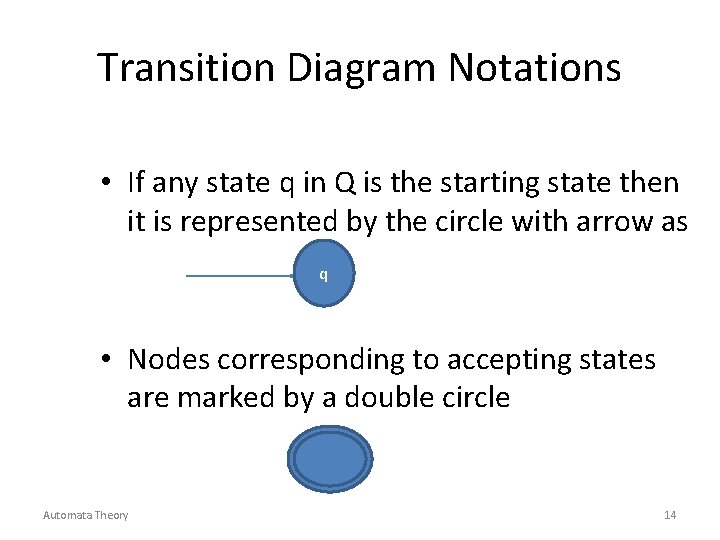
Transition Diagram Notations • If any state q in Q is the starting state then it is represented by the circle with arrow as q • Nodes corresponding to accepting states are marked by a double circle Automata Theory 14

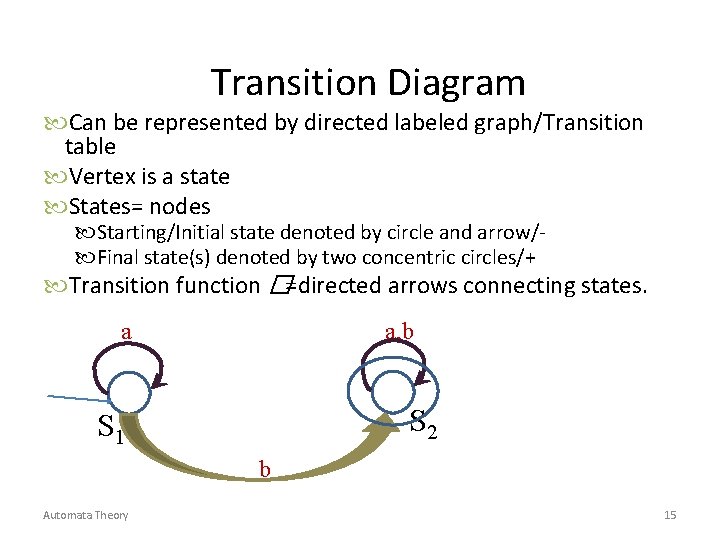
Transition Diagram Can be represented by directed labeled graph/Transition table Vertex is a state States= nodes Starting/Initial state denoted by circle and arrow/ Final state(s) denoted by two concentric circles/+ Transition function �=directed arrows connecting states. a a, b S 2 S 1 b Automata Theory 15

Acceptability of a string A string is accepted by a transition system if • There exist a path from initial state to final state • Path traversed is equal to w Automata Theory 16

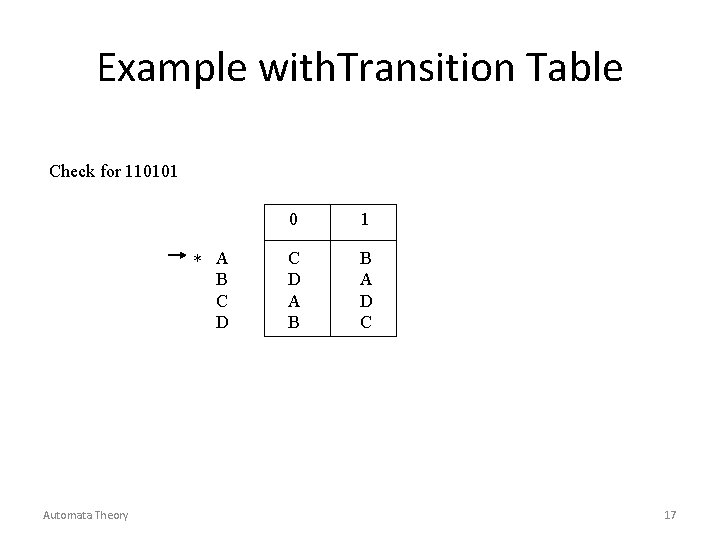
Example with. Transition Table Check for 110101 * A B C D Automata Theory 0 1 C D A B B A D C 17

Example with. Transition Table Solution: - � (A, 110101)= � (B, 10101) � (A, 0101) � (C, 101) � (D, 01) Automata Theory � (B, 1) A* 18

Properties of transition function 1. � (q, λ)=q • It comes back to same state • It requires an input symbol to change the state of a system. 2. � (q, aw)=� (� (q, a), w) � (q, w, a)=� (� (q, w), a) Automata Theory 19