CSCI 3130 Formal Languages and Automata Theory Tutorial

CSCI 3130: Formal Languages and Automata Theory Tutorial 5 Hung Chun Ho Office: SHB 1026 Department of Computer Science & Engineering 1

Agenda • Cocke-Younger-Kasami (CYK) algorithm – Parsing CFG in normal form • Pushdown Automata (PDA) – Design 2

CYK Algorithm Bottom-up Parsing for normal form 3

Cocke-Younger-Kasami Algorithm • Used to parse context-free grammar in Chomsky normal form (or simply normal form) Normal Form Example Every production is of type S AB 1) X YZ A CC | a | c 2) X a B BC | b 3) S ε C CB | BA | c 4

CYK Algorithm - Idea • = Algorithm 2 in Lecture Note (10 L 8. pdf) • Idea: Bottom Up Parsing • Algorithm: Given a string s of length N For k = 1 to N For every substring of length k Determine what variable(s) can derive it 5

CYK Algorithm - Example • CFG S AB A CC | a | c B BC | b C CB | BA | c • Parse abbc 6

CYK Algorithm – Idea (1) • Idea: We parse the strings in this order: • Length-1 substring abbc 7

CYK Algorithm – Idea (1) • Idea: We parse the strings in this order: • Length-2 substring abbc 8

CYK Algorithm – Idea (1) • Idea: We parse the strings in this order: • Length-3 substring abbc • Length-4 substring abbc • Done! 9

CYK Algorithm – Idea (2) • Idea: Parsing of longer substrings depends on parsing of shorter substrings • Example: abb may be decomposed as – ab + b – a + bb • If we know how to parse ab and b (or, a and bb) then we know how to parse abb 10

CYK Algorithm – Substring • Denote sub(i, j) : = substring with start index = i and end index = j • Example: For abbc, sub(2, 4) = bbc • This notation is not to complicate things, but just for the sake of convenience in the following discussion… 11

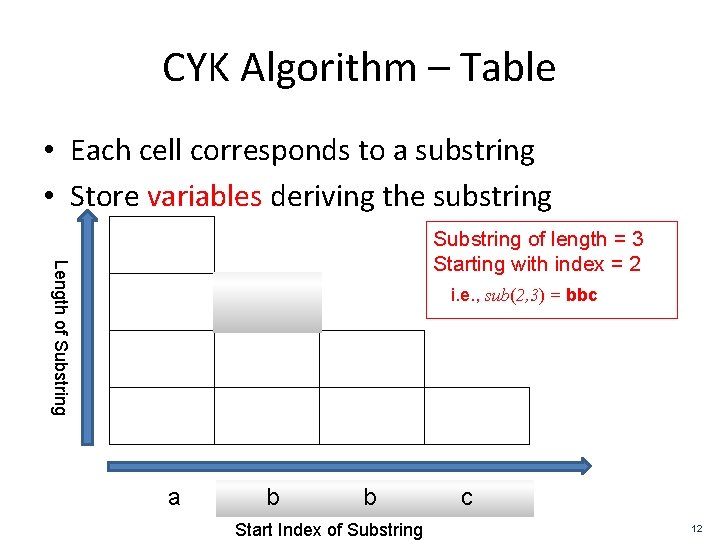
CYK Algorithm – Table • Each cell corresponds to a substring • Store variables deriving the substring Length of Substring of length = 3 Starting with index = 2 i. e. , sub(2, 3) = bbc a b b Start Index of Substring c 12

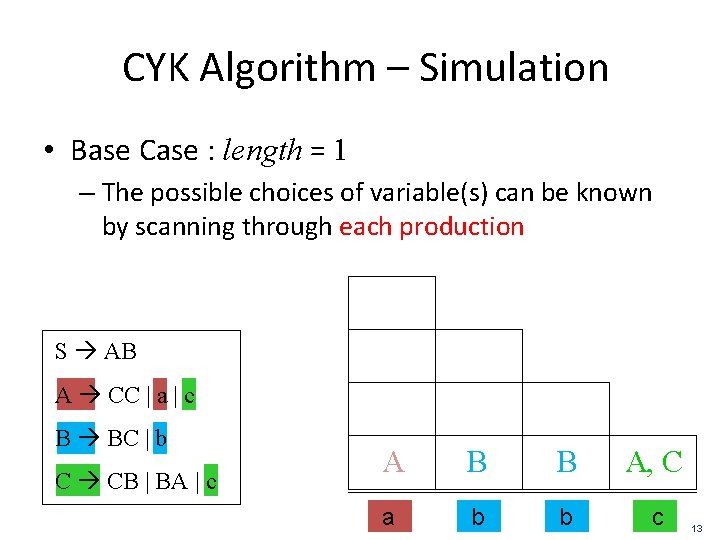
CYK Algorithm – Simulation • Base Case : length = 1 – The possible choices of variable(s) can be known by scanning through each production S AB A CC | a | c B BC | b C CB | BA | c A B B A, C a b b c 13

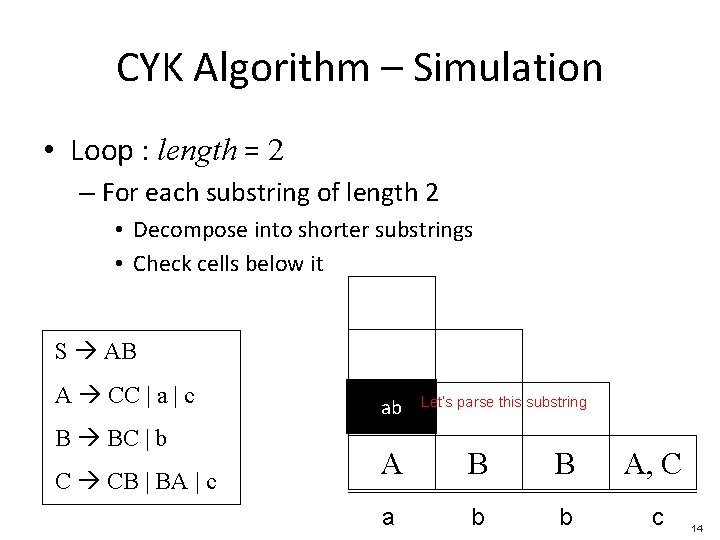
CYK Algorithm – Simulation • Loop : length = 2 – For each substring of length 2 • Decompose into shorter substrings • Check cells below it S AB A CC | a | c B BC | b C CB | BA | c ab Let’s parse this substring A B B A, C a b b c 14

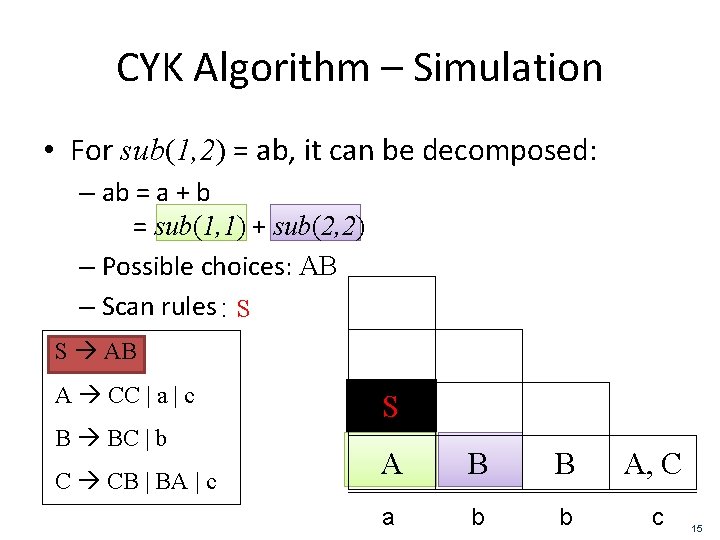
CYK Algorithm – Simulation • For sub(1, 2) = ab, it can be decomposed: – ab = a + b = sub(1, 1) + sub(2, 2) – Possible choices: AB – Scan rules : S S AB A CC | a | c B BC | b C CB | BA | c S A B B A, C a b b c 15

CYK Algorithm – Simulation • For sub(2, 3) = bb, it can be decomposed: – bb = b + b = sub(2, 2) + sub(3, 3) – Possible choices: BB – Scan rules : ∅ No suitable rules are found The CFG cannot parse this substring S AB A CC | a | c B BC | b C CB | BA | c S ∅ A B B A, C a b b c 16

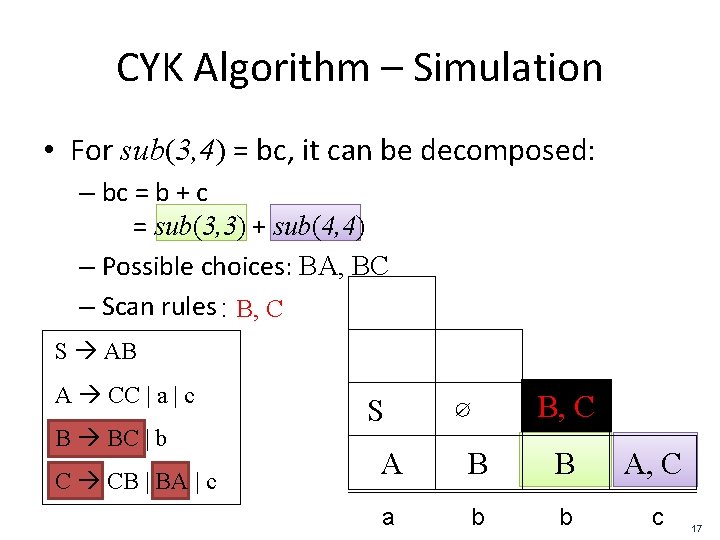
CYK Algorithm – Simulation • For sub(3, 4) = bc, it can be decomposed: – bc = b + c = sub(3, 3) + sub(4, 4) – Possible choices: BA, BC – Scan rules : B, C S AB A CC | a | c B BC | b C CB | BA | c S ∅ B, C A B B A, C a b b c 17

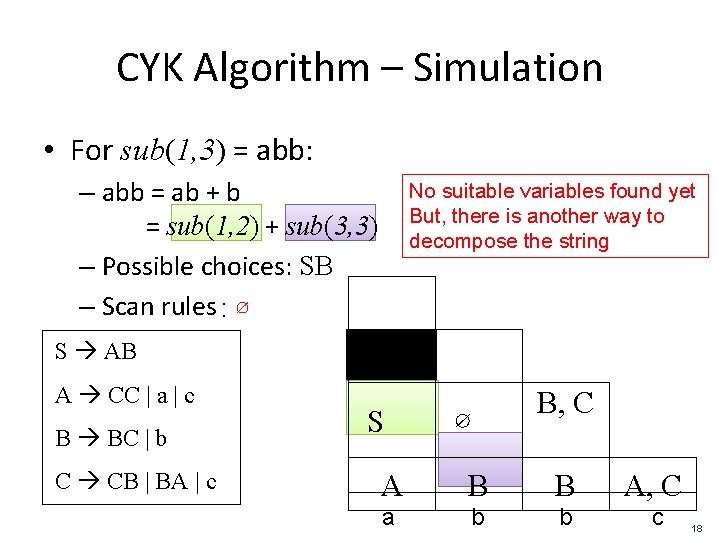
CYK Algorithm – Simulation • For sub(1, 3) = abb: – abb = ab + b = sub(1, 2) + sub(3, 3) – Possible choices: SB – Scan rules : ∅ No suitable variables found yet But, there is another way to decompose the string S AB A CC | a | c B BC | b C CB | BA | c S ∅ B, C A B B A, C a b b c 18

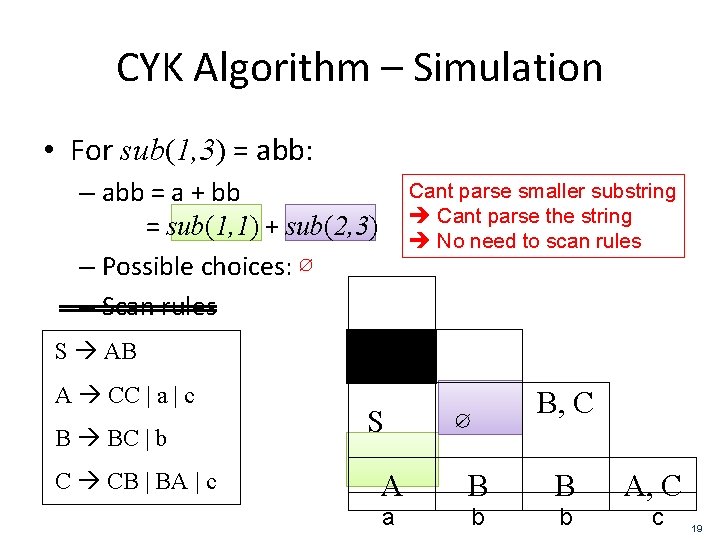
CYK Algorithm – Simulation • For sub(1, 3) = abb: – abb = a + bb = sub(1, 1) + sub(2, 3) – Possible choices: ∅ – Scan rules Cant parse smaller substring Cant parse the string No need to scan rules S AB A CC | a | c B BC | b C CB | BA | c S ∅ B, C A B B A, C a b b c 19

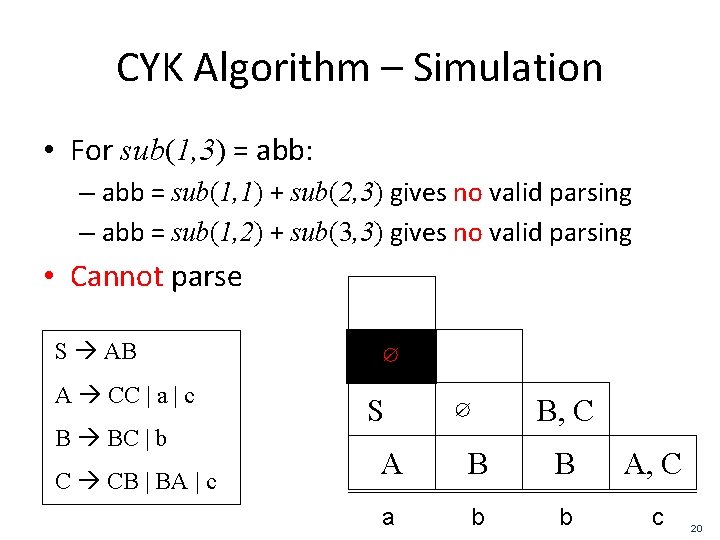
CYK Algorithm – Simulation • For sub(1, 3) = abb: – abb = sub(1, 1) + sub(2, 3) gives no valid parsing – abb = sub(1, 2) + sub(3, 3) gives no valid parsing • Cannot parse S AB A CC | a | c B BC | b C CB | BA | c ∅ S ∅ B, C A B B A, C a b b c 20

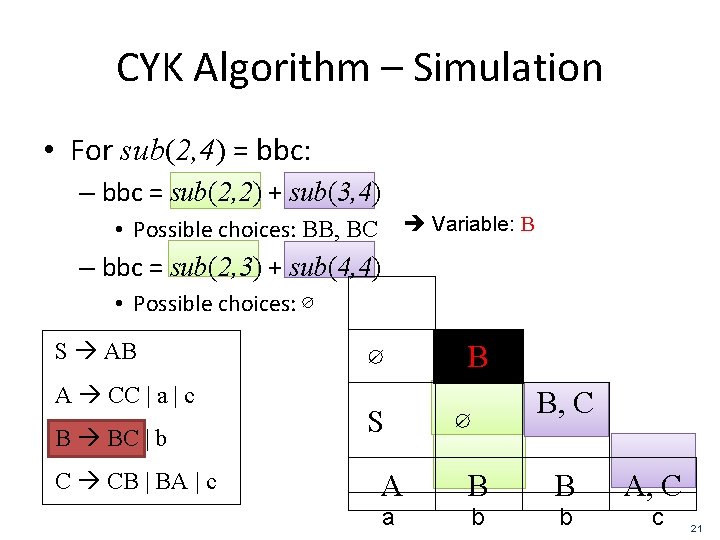
CYK Algorithm – Simulation • For sub(2, 4) = bbc: – bbc = sub(2, 2) + sub(3, 4) Variable: B • Possible choices: BB, BC – bbc = sub(2, 3) + sub(4, 4) • Possible choices: ∅ S AB A CC | a | c B BC | b C CB | BA | c ∅ S B ∅ B, C A B B A, C a b b c 21

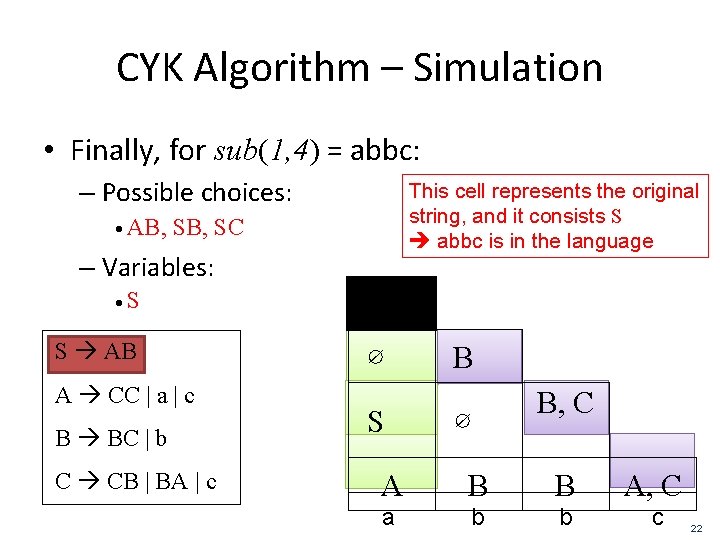
CYK Algorithm – Simulation • Finally, for sub(1, 4) = abbc: – Possible choices: This cell represents the original string, and it consists S abbc is in the language • AB, SC – Variables: • S S AB A CC | a | c B BC | b C CB | BA | c ∅ S B ∅ B, C A B B A, C a b b c 22

CYK Algorithm – Parse Tree • abbc is in the language! • How to obtain the parse tree? – Tracing back the derivations: • sub(1, 4) is derived using S AB from sub(1, 1) and sub(2, 4) • sub(1, 1) is derived using A a • sub(2, 4) is derived using B BC from sub(2, 2) and sub(3, 4) • … • So, record also the used derivations! 23

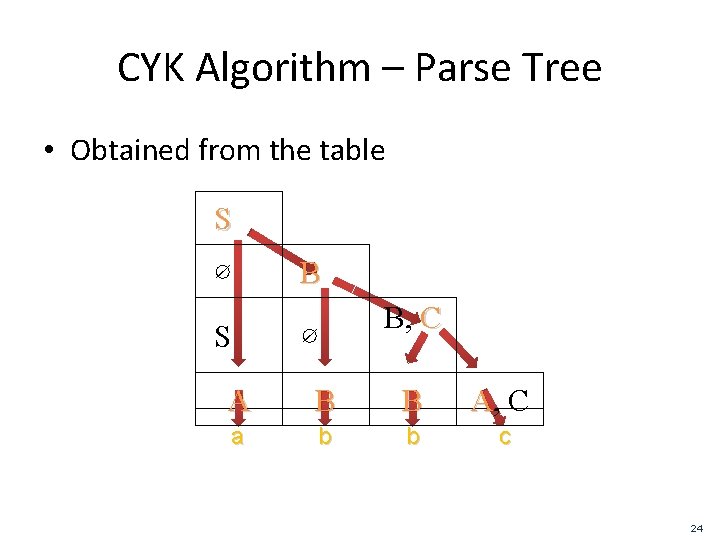
CYK Algorithm – Parse Tree • Obtained from the table S B ∅ S ∅ B, C A B B A, C a b b c 24

CYK Algorithm – Conclusion • A bottom up parsing algorithm – Dynamic Programming – Solution of a subproblem (parsing of a substring) depends on that of smaller subproblems • Before employing CYK Algorithm, convert the grammar into normal form – Remove ε-productions – Remove unit-productions 25

CYK Algorithm – Detailed D = “On input w = w 1 w 2…wn: If w = ε, and S ε is rule, Accept For i = 1 to n: For each variable A: Test whether A b is a rule, where b = wi. If so, place A in table(i, i). For l = 2 to n: For i = 1 to n – l + 1: Let j = i + l – 1, For k = i to j – 1: For each rule A BC: If table(i, k) contains B and table(k+1, j) contains C Put A in table(i, j) If S is in table (1, n), accept. Otherwise, reject. ” 26

Pushdown Automata NFA with infinite memory/states 27

Pushdown Automata • PDA ~= NFA, with a stack of memory • Transition: – NFA – Depends on input – PDA – Depends on input and top of stack (possibly ε) • Push a symbol to stack (possibly ε) • Pop a symbol to stack • Read a terminal on string (possibly ε) • Transitions are non-deterministic 28

Pushdown Automata and NFA • Accept: – NFA – Go to an Accept state – PDA – Go to an Accept state 29

PDA – Example 1 • Given the following language: L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, S = {0, 1} • Design a PDA for it 30

PDA – Example 1 - Idea • Idea: The input has two sections – First half • All ‘ 0’s – Second half • All ‘ 1’s • #‘ 1 depends on #‘ 0’ – #‘ 0’ ≤ #‘ 1’ ≤ #‘ 0’ × 2 31

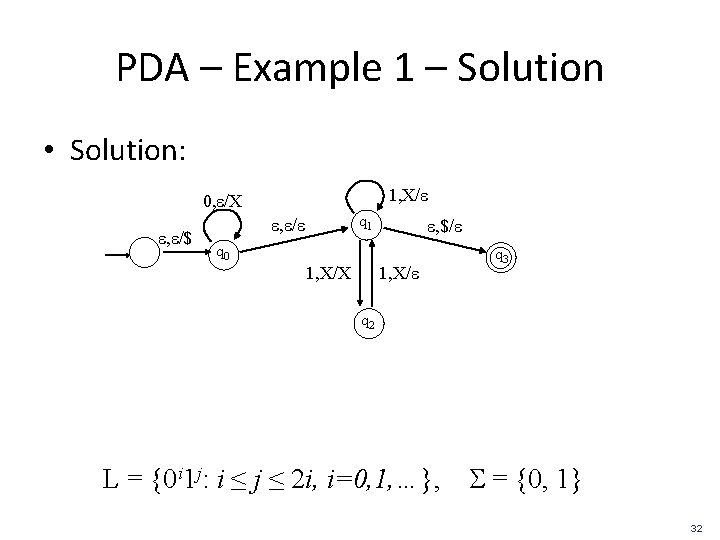
PDA – Example 1 – Solution • Solution: 1, X/e 0, e/X e, e/$ q 1 e, e/e e, $/e q 0 1, X/X 1, X/e q 3 q 2 L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, S = {0, 1} 32

PDA – Example 1 – Explain • Solution: 1, X/e 0, e/X e, e/$ q 1 e, e/e e, $/e q 0 1, X/X q 3 1, X/e q 2 • Let’s try some string… w = 00111 – See white board for simulation… L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, S = {0, 1} 33

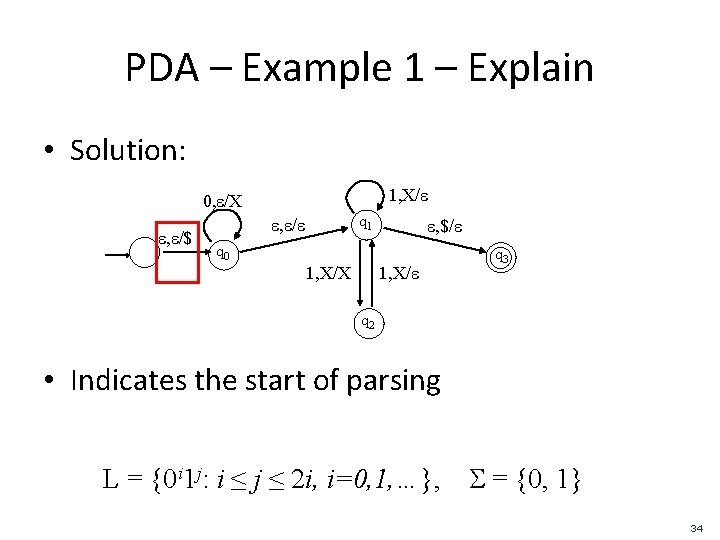
PDA – Example 1 – Explain • Solution: 1, X/e 0, e/X e, e/$ q 1 e, e/e e, $/e q 0 1, X/X 1, X/e q 3 q 2 • Indicates the start of parsing L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, S = {0, 1} 34

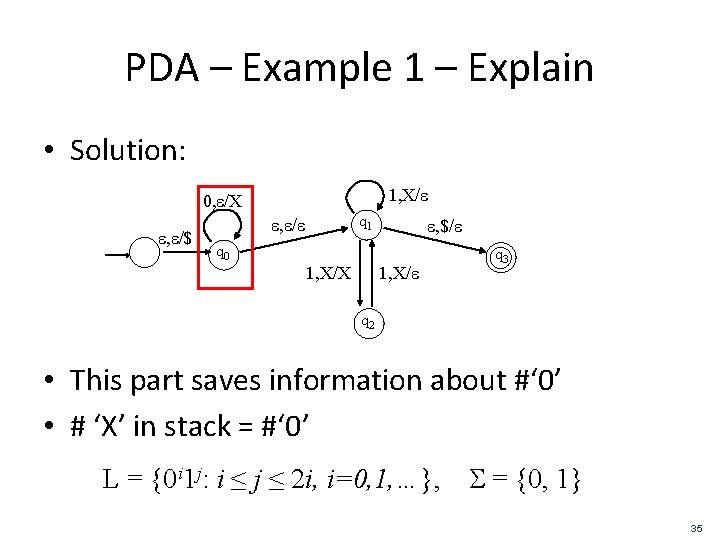
PDA – Example 1 – Explain • Solution: 1, X/e 0, e/X e, e/$ q 1 e, e/e e, $/e q 0 1, X/X 1, X/e q 3 q 2 • This part saves information about #‘ 0’ • # ‘X’ in stack = #‘ 0’ L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, S = {0, 1} 35

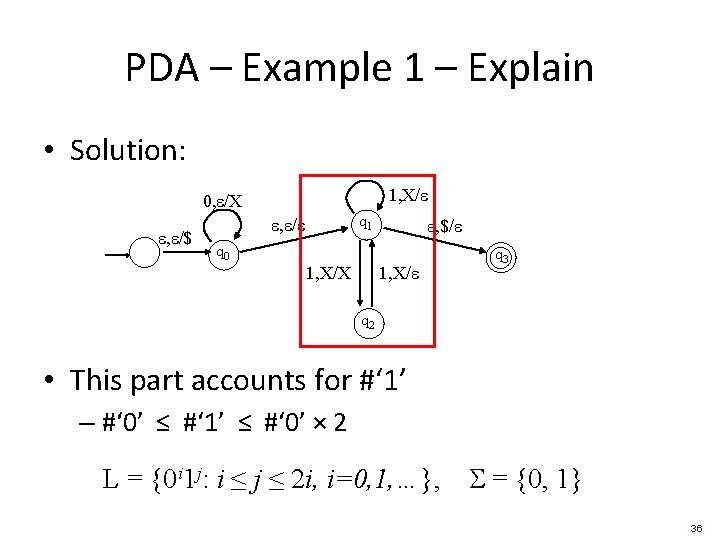
PDA – Example 1 – Explain • Solution: 1, X/e 0, e/X e, e/$ q 1 e, e/e e, $/e q 0 1, X/X 1, X/e q 3 q 2 • This part accounts for #‘ 1’ – #‘ 0’ ≤ #‘ 1’ ≤ #‘ 0’ × 2 L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, S = {0, 1} 36

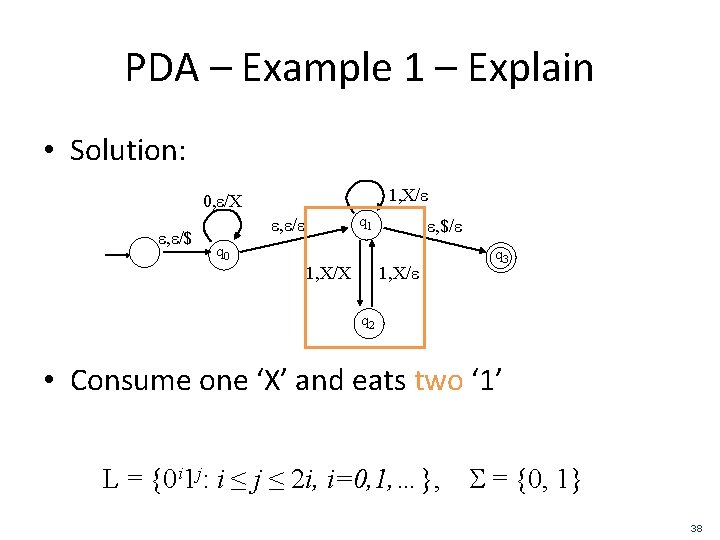
PDA – Example 1 – Explain • Solution: 1, X/e 0, e/X e, e/$ q 1 e, e/e e, $/e q 0 1, X/X 1, X/e q 3 q 2 • Consume one ‘X’ and eats one ‘ 1’ L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, S = {0, 1} 37

PDA – Example 1 – Explain • Solution: 1, X/e 0, e/X e, e/$ q 1 e, e/e e, $/e q 0 1, X/X 1, X/e q 3 q 2 • Consume one ‘X’ and eats two ‘ 1’ L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, S = {0, 1} 38

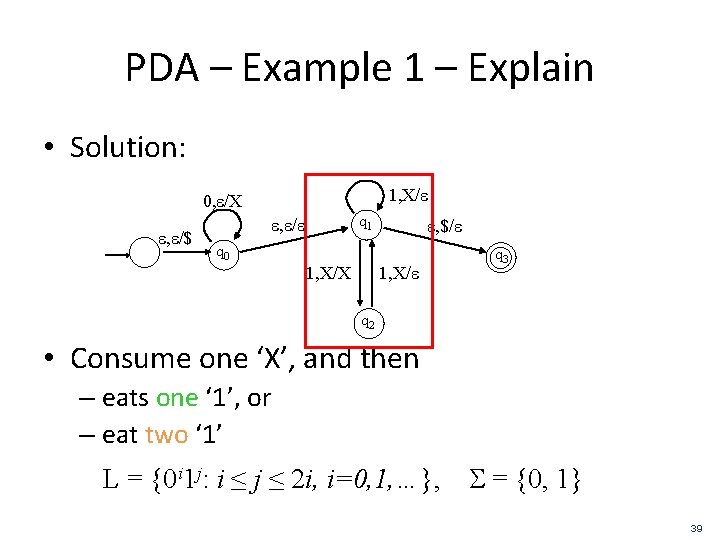
PDA – Example 1 – Explain • Solution: 1, X/e 0, e/X e, e/$ q 1 e, e/e e, $/e q 0 1, X/X 1, X/e q 3 q 2 • Consume one ‘X’, and then – eats one ‘ 1’, or – eat two ‘ 1’ L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, S = {0, 1} 39

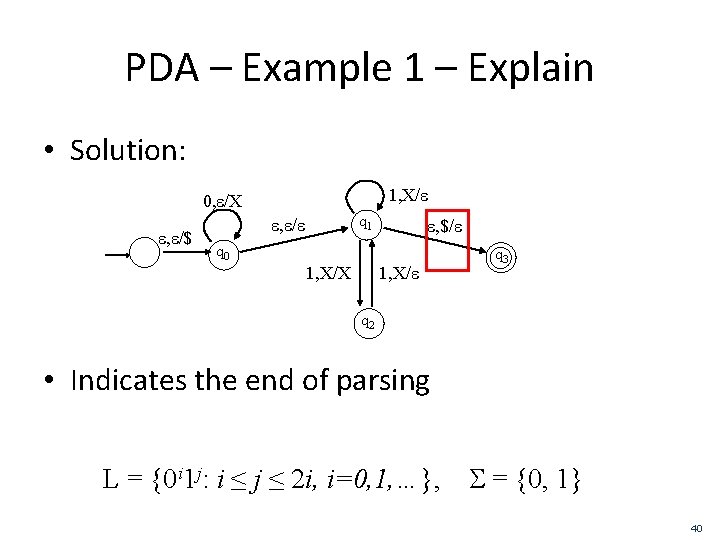
PDA – Example 1 – Explain • Solution: 1, X/e 0, e/X e, e/$ q 1 e, e/e e, $/e q 0 1, X/X 1, X/e q 3 q 2 • Indicates the end of parsing L = {0 i 1 j: i ≤ j ≤ 2 i, i=0, 1, …}, S = {0, 1} 40

PDA – Example 2 • Given the following language: L = { aibjckdl: i, j, k, l=0, 1, …; i+k=j+l }, where the alphabet Σ= {a, b, c, d} • Design a PDA for it 41

PDA – Example 2 – Idea • Idea: – Sequentially read (multiple) ‘a’, ‘b’, ‘c’ and ‘d’ – Maintain: • #‘a’ + #‘c’ • #‘b’ + #‘d’ – If these numbers equal • Accept 42

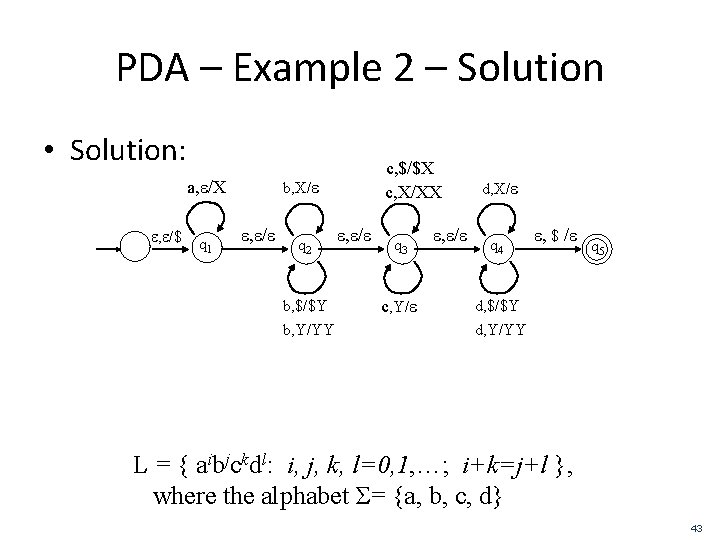
PDA – Example 2 – Solution • Solution: b, X/e a, e/X e, e/$ q 1 c, $/$X c, X/XX e, e/e q 2 b, $/$Y b, Y/YY e, e/e q 3 c, Y/e e, e/e d, X/e q 4 e, $ /e q 5 d, $/$Y d, Y/YY L = { aibjckdl: i, j, k, l=0, 1, …; i+k=j+l }, where the alphabet Σ= {a, b, c, d} 43

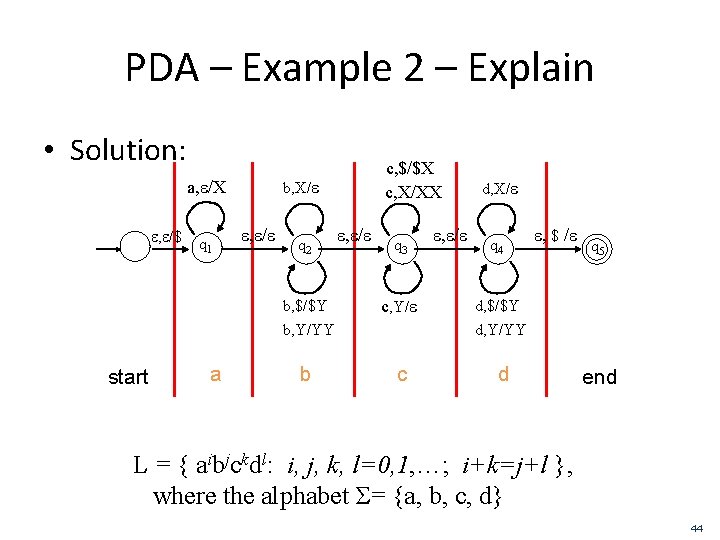
PDA – Example 2 – Explain • Solution: b, X/e a, e/X e, e/$ q 1 c, $/$X c, X/XX e, e/e q 2 b, $/$Y e, e/e q 3 c, Y/e b, Y/YY start a b e, e/e d, X/e q 4 e, $ /e q 5 d, $/$Y d, Y/YY c d end L = { aibjckdl: i, j, k, l=0, 1, …; i+k=j+l }, where the alphabet Σ= {a, b, c, d} 44

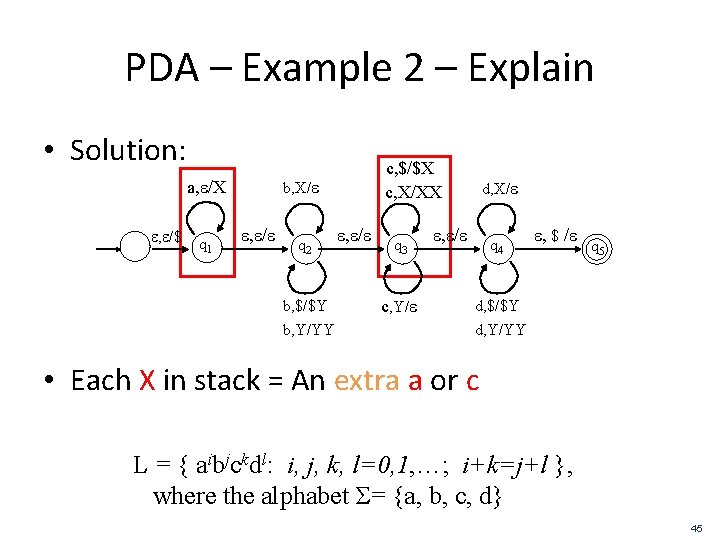
PDA – Example 2 – Explain • Solution: b, X/e a, e/X e, e/$ q 1 c, $/$X c, X/XX e, e/e q 2 b, $/$Y b, Y/YY e, e/e q 3 c, Y/e d, X/e e, e/e q 4 e, $ /e q 5 d, $/$Y d, Y/YY • Each X in stack = An extra a or c L = { aibjckdl: i, j, k, l=0, 1, …; i+k=j+l }, where the alphabet Σ= {a, b, c, d} 45

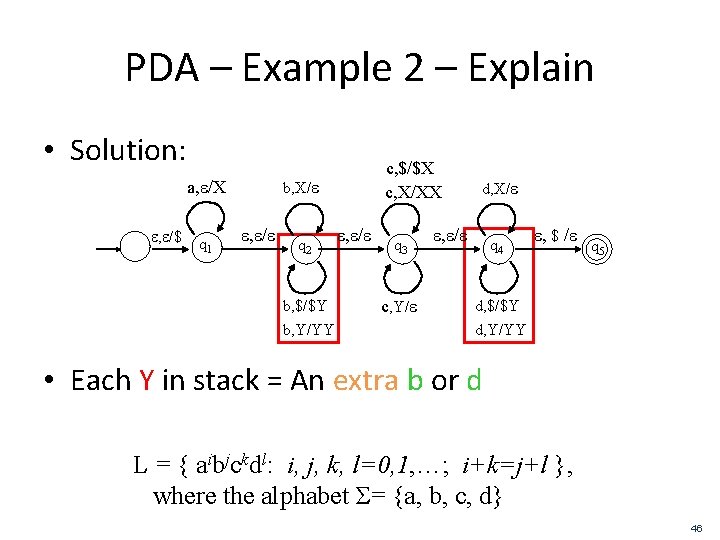
PDA – Example 2 – Explain • Solution: b, X/e a, e/X e, e/$ q 1 c, $/$X c, X/XX e, e/e q 2 b, $/$Y b, Y/YY e, e/e q 3 c, Y/e d, X/e e, e/e q 4 e, $ /e q 5 d, $/$Y d, Y/YY • Each Y in stack = An extra b or d L = { aibjckdl: i, j, k, l=0, 1, …; i+k=j+l }, where the alphabet Σ= {a, b, c, d} 46

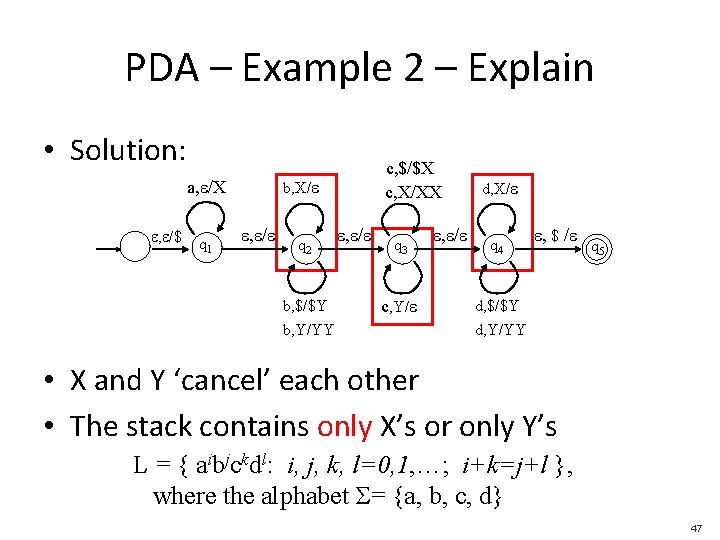
PDA – Example 2 – Explain • Solution: b, X/e a, e/X e, e/$ q 1 c, $/$X c, X/XX e, e/e q 2 b, $/$Y b, Y/YY e, e/e q 3 c, Y/e e, e/e d, X/e q 4 e, $ /e q 5 d, $/$Y d, Y/YY • X and Y ‘cancel’ each other • The stack contains only X’s or only Y’s L = { aibjckdl: i, j, k, l=0, 1, …; i+k=j+l }, where the alphabet Σ= {a, b, c, d} 47

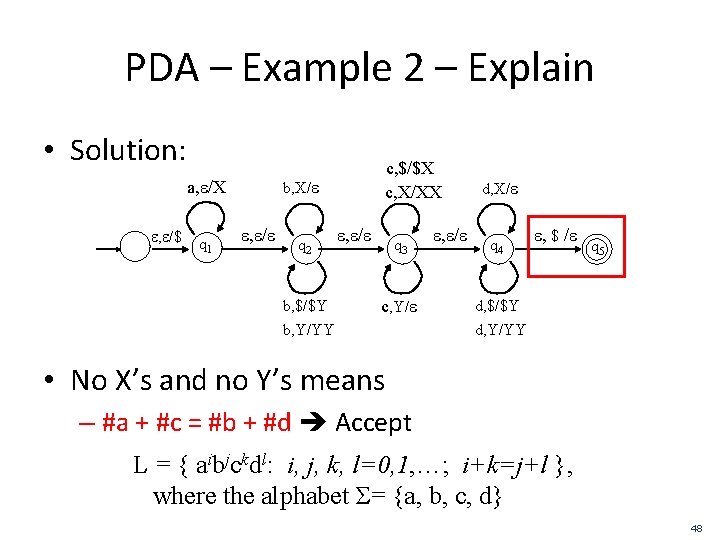
PDA – Example 2 – Explain • Solution: b, X/e a, e/X e, e/$ q 1 c, $/$X c, X/XX e, e/e q 2 b, $/$Y e, e/e q 3 c, Y/e b, Y/YY e, e/e d, X/e q 4 e, $ /e q 5 d, $/$Y d, Y/YY • No X’s and no Y’s means – #a + #c = #b + #d Accept L = { aibjckdl: i, j, k, l=0, 1, …; i+k=j+l }, where the alphabet Σ= {a, b, c, d} 48