CSCI 3130 Formal Languages and Automata Theory Tutorial

CSCI 3130: Formal Languages and Automata Theory Tutorial 4 Hung Chun Ho Office: SHB 1026 Department of Computer Science & Engineering 1

Agenda • DFA Minimization – Algorithm – 2 Examples • Context Free Grammar (CFG) – Design – Parse Tree 2

DFA Minimization 3

DFA Minimization 0 q 000 0 1 q 001 1 … q 01 1 q 10 q 0 0 0 qe 1 q 1 1 q 2 q 111 1 1 q 11 1 1 … 0 q 3 q 101 … q 00 1 … 1 0 q 1 1 0 0 0 q 0 We will show to turn any DFA for L into the minimal DFA for L 4

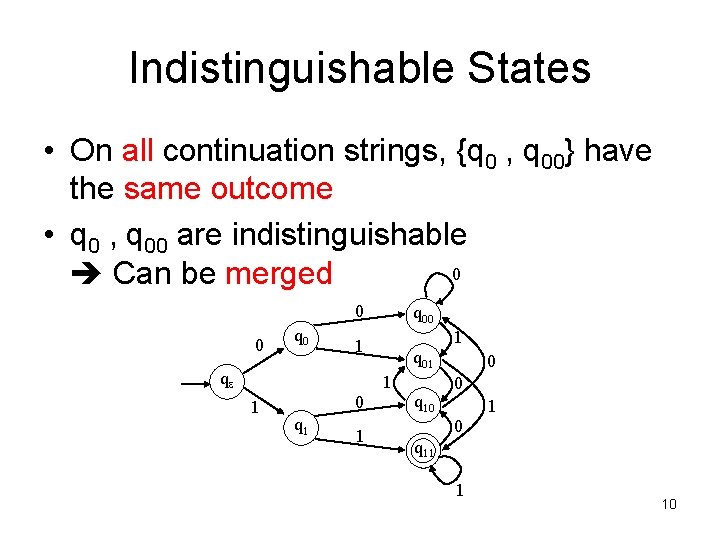
DFA Minimization • After we design a DFA, there may be some redundant states – They have the same “function” – They are indistinguishable – No matter what happens in the future (inputs), they will have the same fate (accept/reject)! • We can merge indistinguishable states into groups 5

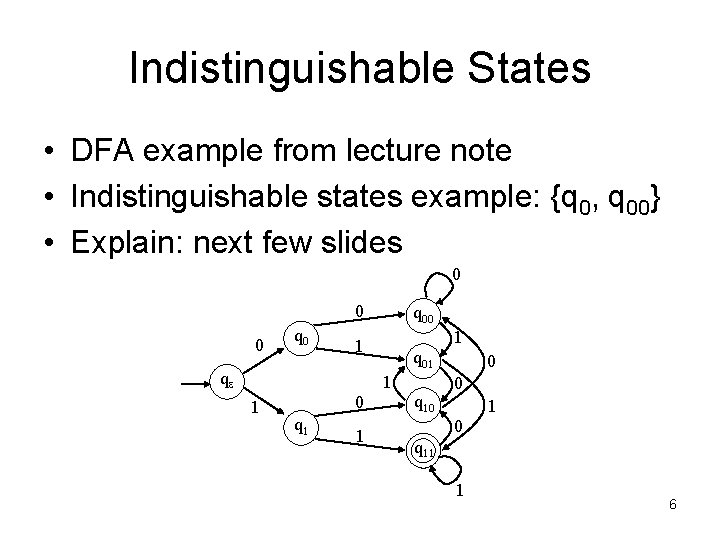
Indistinguishable States • DFA example from lecture note • Indistinguishable states example: {q 0, q 00} • Explain: next few slides 0 0 0 q 00 1 1 qe q 01 1 1 0 q 1 1 q 10 0 1 q 11 1 6

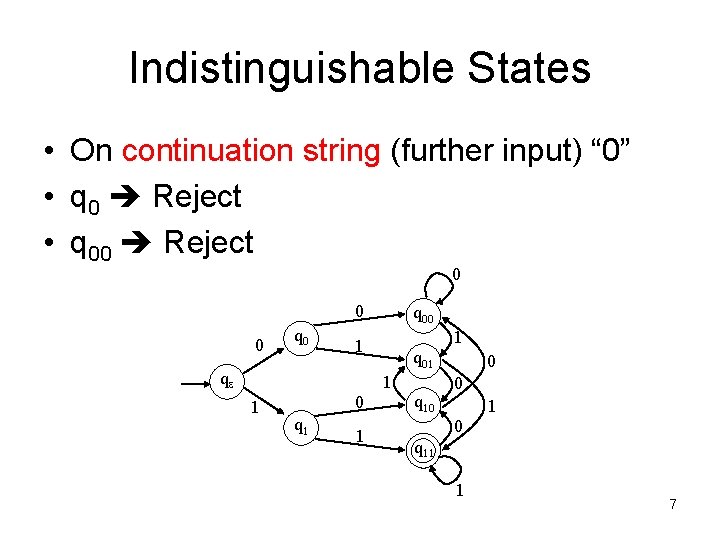
Indistinguishable States • On continuation string (further input) “ 0” • q 0 Reject • q 00 Reject 0 0 0 q 00 1 1 qe q 01 1 1 0 q 1 1 q 10 0 1 q 11 1 7

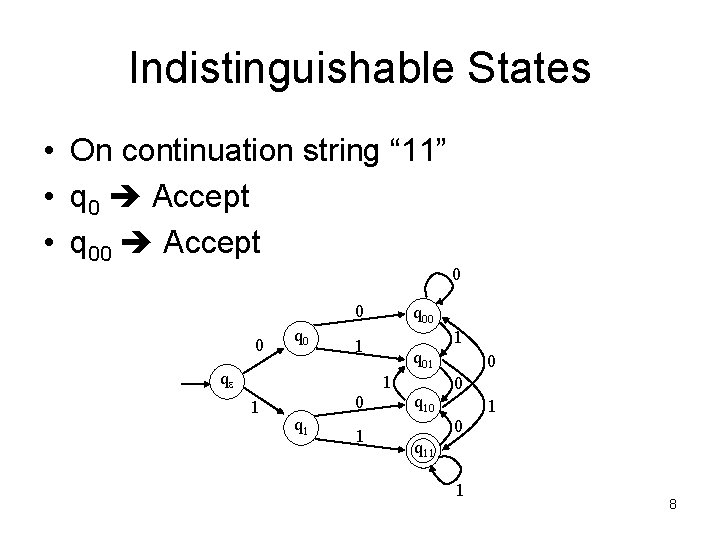
Indistinguishable States • On continuation string “ 11” • q 0 Accept • q 00 Accept 0 0 q 00 1 1 qe q 01 1 1 0 q 10 0 1 q 11 1 8

Indistinguishable States • On continuation string “ 01011” • q 0 Accept • q 00 Accept 0 0 0 q 00 1 1 qe q 01 1 1 0 q 1 1 q 10 0 1 q 11 1 9

Indistinguishable States • On all continuation strings, {q 0 , q 00} have the same outcome • q 0 , q 00 are indistinguishable 0 Can be merged 0 0 q 00 1 1 qe q 01 1 1 0 q 1 1 q 10 0 1 q 11 1 10

How to find? • Infinitely many continuation states – A bit difficult to find indistinguishable states directly • We do the reverse: – To recognize distinguishable states – Pair of states, s. t. there is a continuation string, causing them have different “fates” – (De Morgan’s Law, still remember? ) 11

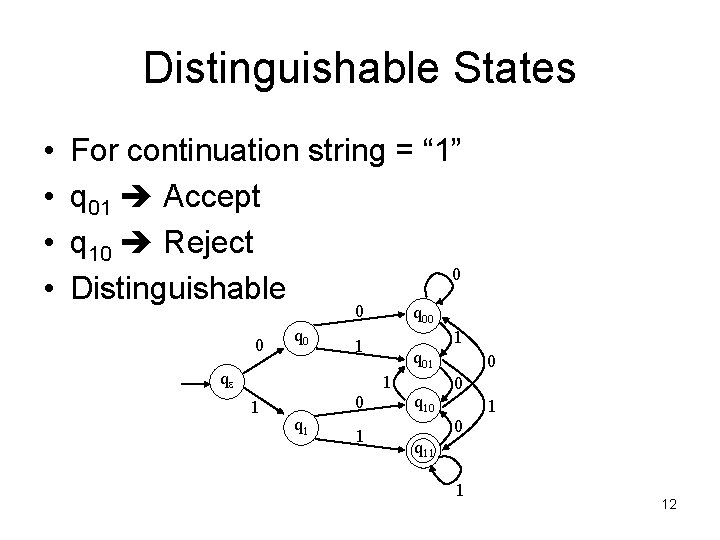
Distinguishable States • • For continuation string = “ 1” q 01 Accept q 10 Reject 0 Distinguishable 0 0 q 00 1 1 qe q 01 1 1 0 q 1 1 q 10 0 1 q 11 1 12

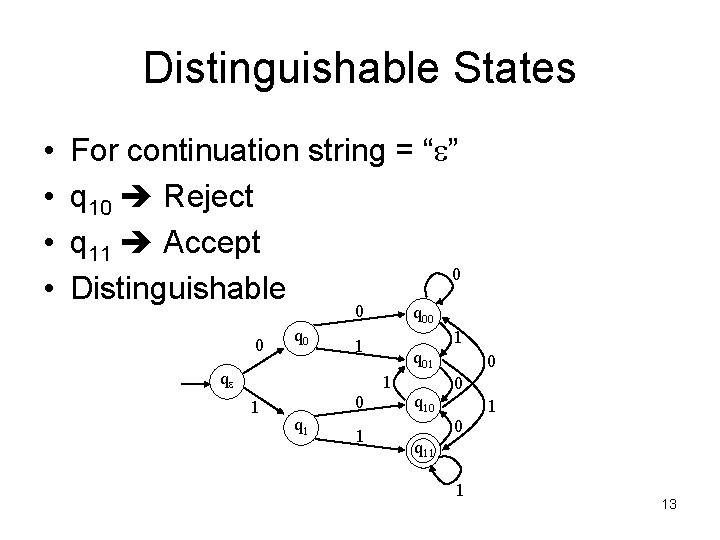
Distinguishable States • • For continuation string = “e” q 10 Reject q 11 Accept 0 Distinguishable 0 0 q 00 1 1 qe q 01 1 1 0 q 1 1 q 10 0 1 q 11 1 13

Distinguishable States • 2 states are distinguishable, if there is a continuation string, that bring them different fate!! (Accept / Reject) – Try all continuation strings? How? • Idea: – For any pair of {Accept, Reject} states, they are distinguishable – For these pairs, walk k transitions backward, mark the obtained pairs as distinguishable 14

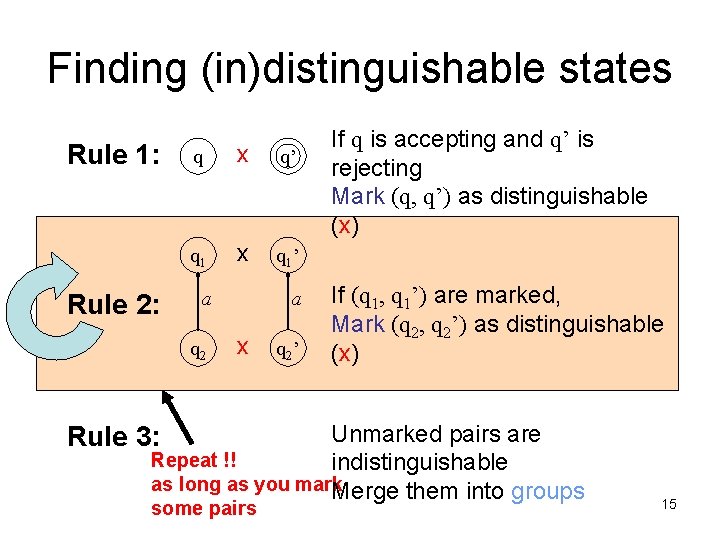
Finding (in)distinguishable states Rule 1: Rule 2: q x q’ q 1 x q 1’ a q 2 a x q 2’ If q is accepting and q’ is rejecting Mark (q, q’) as distinguishable (x) If (q 1, q 1’) are marked, Mark (q 2, q 2’) as distinguishable (x) Unmarked pairs are Repeat !! indistinguishable as long as you mark Merge them into groups Rule 3: some pairs 15

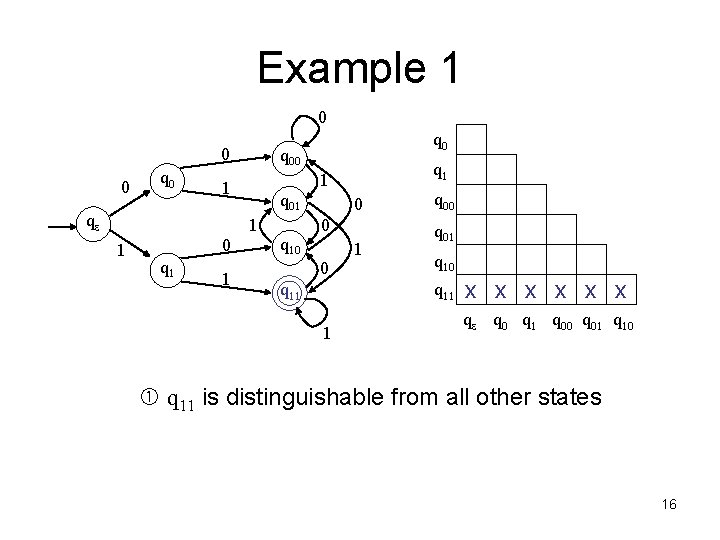
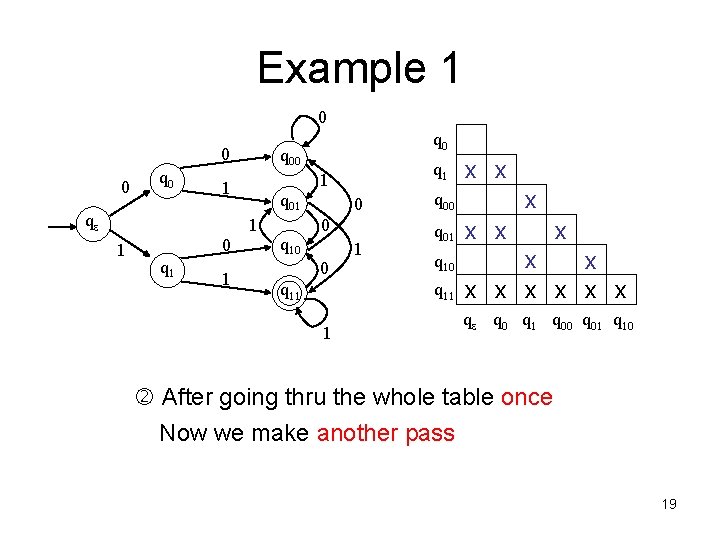
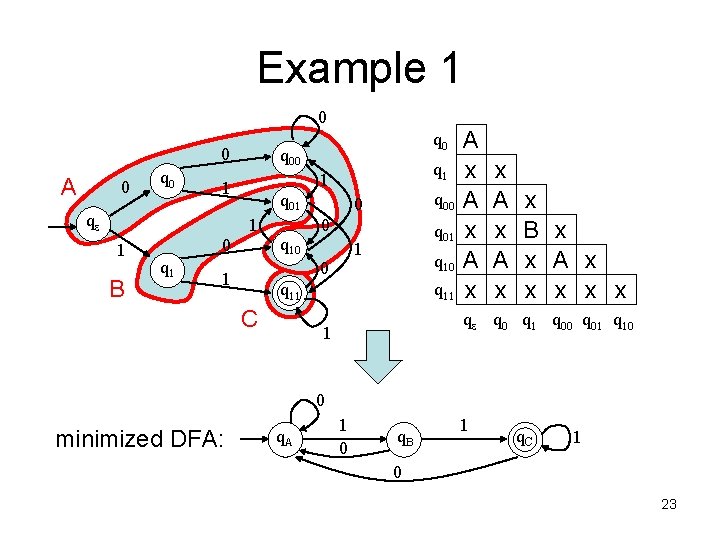
Example 1 0 0 0 q 00 q 01 1 1 0 q 1 1 1 qe q 0 q 10 0 q 11 1 q 00 q 01 q 10 q 11 1 x x x qe q 0 q 1 q 00 q 01 q 10 q 11 is distinguishable from all other states 16

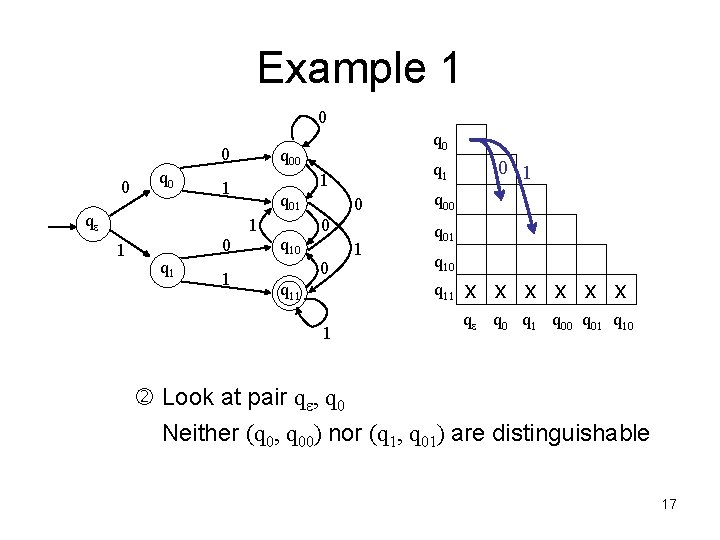
Example 1 0 0 0 q 00 q 01 1 1 0 q 1 1 1 qe q 0 q 10 0 q 11 1 q 00 q 01 q 10 q 11 1 0 1 x x x qe q 0 q 1 q 00 q 01 q 10 Look at pair qe, q 0 Neither (q 0, q 00) nor (q 1, q 01) are distinguishable 17

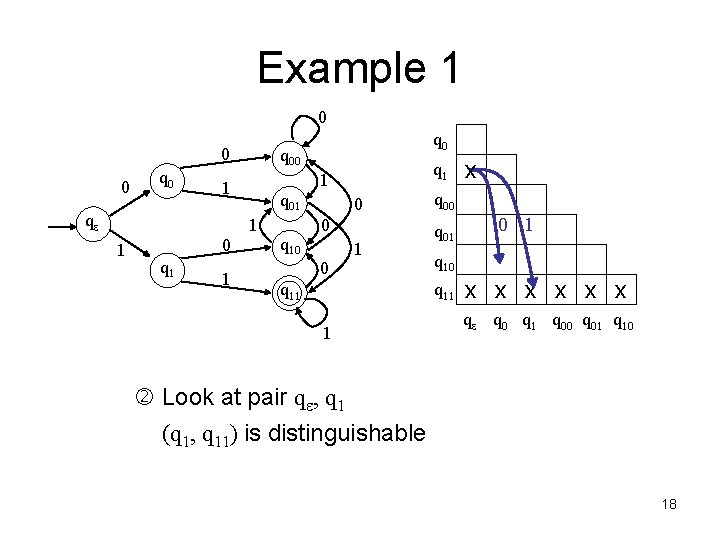
Example 1 0 0 0 q 00 q 01 1 1 0 q 1 1 1 qe q 0 q 10 0 1 q 11 q 00 q 01 0 1 q 10 q 11 1 x x x x qe q 0 q 1 q 00 q 01 q 10 Look at pair qe, q 1 (q 1, q 11) is distinguishable 18

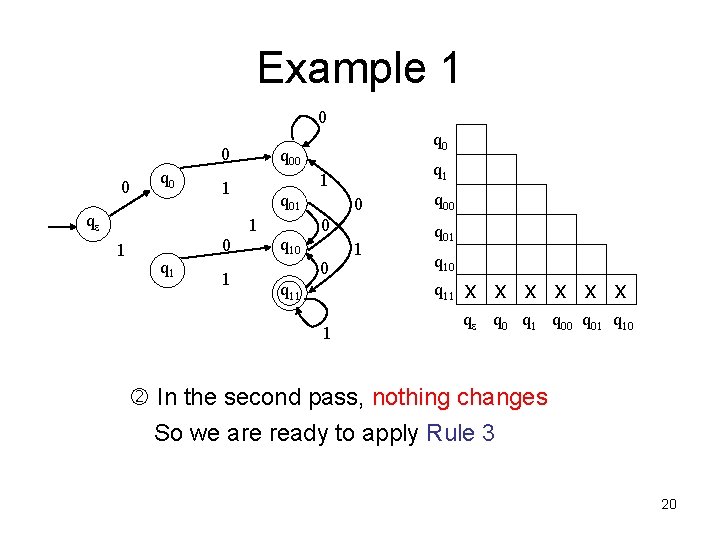
Example 1 0 0 0 q 00 q 01 1 1 0 q 1 1 1 qe q 0 q 10 0 q 11 1 x q 00 q 01 x x q 10 x x x x q 11 1 x x x qe q 0 q 1 q 00 q 01 q 10 After going thru the whole table once Now we make another pass 19

Example 1 0 0 0 q 00 q 01 1 1 0 q 1 1 1 qe q 0 q 10 0 q 11 1 x q 00 q 01 x x q 10 x x x x q 11 1 x x x qe q 0 q 1 q 00 q 01 q 10 In the second pass, nothing changes So we are ready to apply Rule 3 20

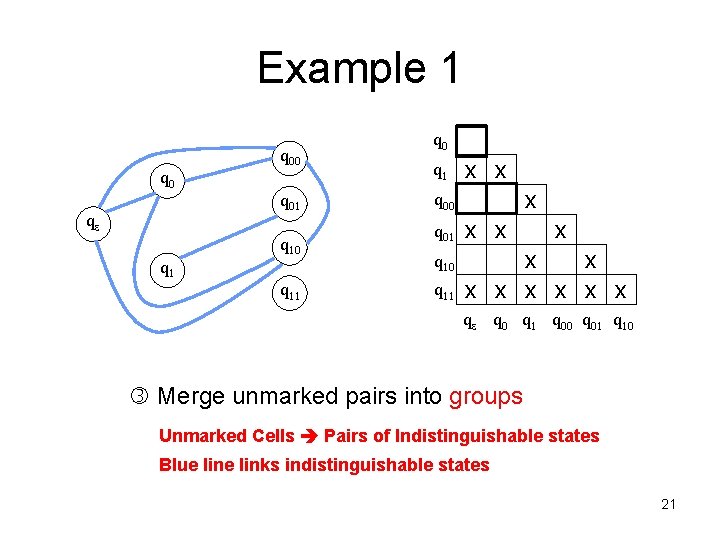
Example 1 q 0 qe q 1 q 00 q 01 q 10 q 11 q 0 q 1 x x x q 00 q 01 x x q 10 x x x x q 11 x qe q 0 q 1 q 00 q 01 q 10 Merge unmarked pairs into groups Unmarked Cells Pairs of Indistinguishable states Blue links indistinguishable states 21

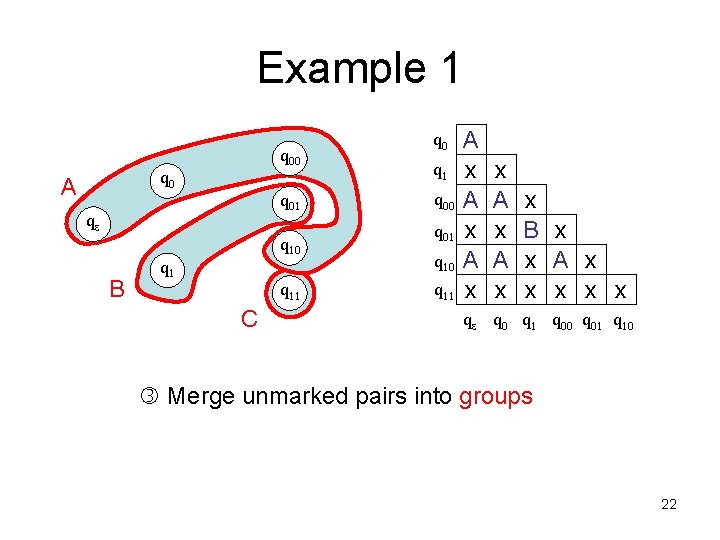
Example 1 q 00 q 0 A q 01 qe B q 10 q 11 C q 0 q 1 q 00 q 01 q 10 q 11 A x A x x B x x A x x x qe q 0 q 1 q 00 q 01 q 10 Merge unmarked pairs into groups 22

Example 1 0 0 A 0 q 00 q 01 1 1 B 0 q 1 1 1 qe q 0 q 10 0 q 01 1 0 1 q 00 0 q 11 C q 11 A x A x x B x x A x x x qe q 0 q 1 q 00 q 01 q 10 1 0 minimized DFA: q. A 1 0 q. B 1 q. C 1 0 23

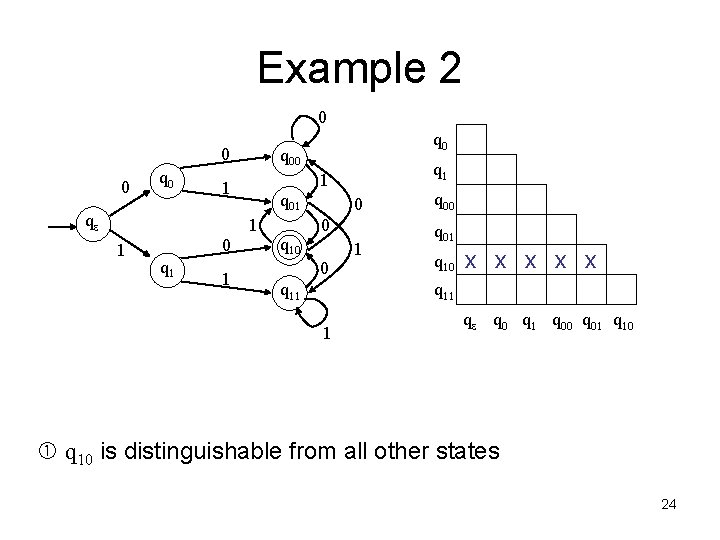
Example 2 0 0 0 q 00 q 01 1 1 0 q 1 1 1 qe q 0 q 10 0 q 11 1 q 00 q 01 q 10 x x x q 11 1 qe q 0 q 1 q 00 q 01 q 10 is distinguishable from all other states 24

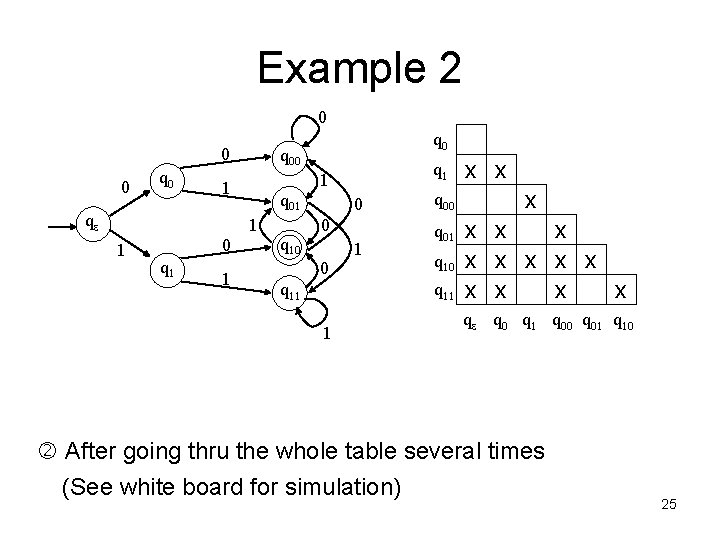
Example 2 0 0 0 q 00 q 01 1 1 0 q 1 1 1 qe q 0 q 10 0 q 11 1 q 00 q 01 q 10 q 11 1 x x x x qe q 0 q 1 q 00 q 01 q 10 After going thru the whole table several times (See white board for simulation) 25

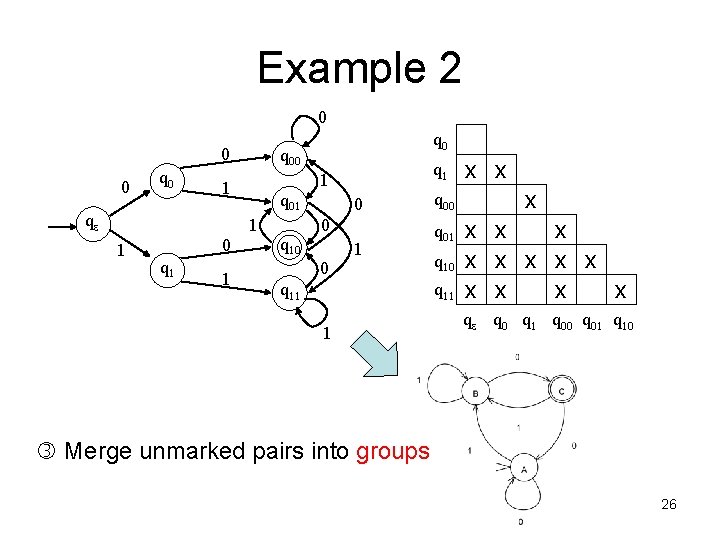
Example 2 0 0 0 q 00 q 01 1 1 0 q 1 1 1 qe q 0 q 10 0 1 q 11 q 00 q 01 q 10 q 11 1 x x x x qe q 0 q 1 q 00 q 01 q 10 Merge unmarked pairs into groups 26

Why it works? • For a pair of states, there is a continuation string that bring them different fates – Distinguishable • Idea: For any pair of {Accept, Reject} states, they are distinguishable, mark them – These pairs have a length-0 continuation string that distinguishes them • 1 step backward, mark them as distinguishable – These pairs have a length-1 continuation string that distinguishes them 27

Why it works? • 1 further step backward, mark – These pairs have a length-2 continuation string that distinguishes them • 1 further step backward, mark – These pairs have a length-3 continuation string that distinguishes them • So-on … 28

Context Free Grammar 29

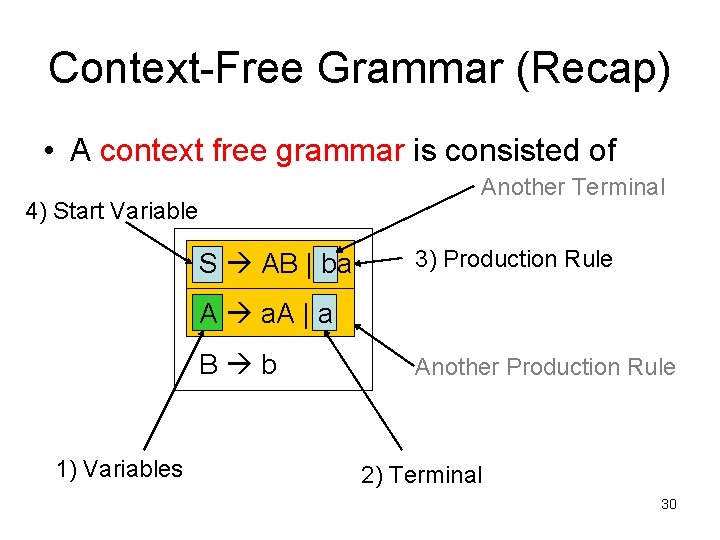
Context-Free Grammar (Recap) • A context free grammar is consisted of Another Terminal 4) Start Variable S AB | ba 3) Production Rule A a. A | a B b 1) Variables Another Production Rule 2) Terminal 30

Context-Free Grammar (Recap) • A string is said to belong to the language (of the CFG) if it can be derived from the start variable = Apply Production Rule CFG Example Derivation S AB | ba S AB A a. A | a a. AB B b aa. B Therefore, aab belongs to the language aab 31

Why CFG? • L = {w = 0 n 1 n : n is an positive integer} • L is not a regular language – Proved by “Pumping Lemma” • A Context-Free Grammar can describe it S 0 S 1 S 01 • Thus, CFG is more general than regular expression – Recall: NFA Regular Expression DFA 32

CFG Design • Given a context-free language, design the CFG • L = { ab-string, w : Number of a’s < Number of b’s } • Some time for you to get into think… 1 min S ? … 33

CFG Design (Con’t) • Idea: Bottom-up – Shortest string in L : “b” – Given a string in L, we can expand it, s. t. it is still in L – i. e. , Add terminals, while not violating the constraints 34

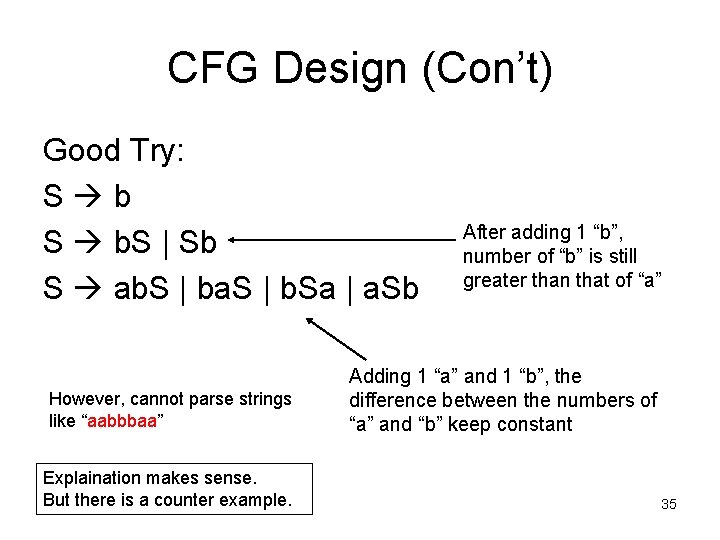
CFG Design (Con’t) Good Try: S b S b. S | Sb S ab. S | ba. S | b. Sa | a. Sb However, cannot parse strings like “aabbbaa” Explaination makes sense. But there is a counter example. After adding 1 “b”, number of “b” is still greater than that of “a” Adding 1 “a” and 1 “b”, the difference between the numbers of “a” and “b” keep constant 35

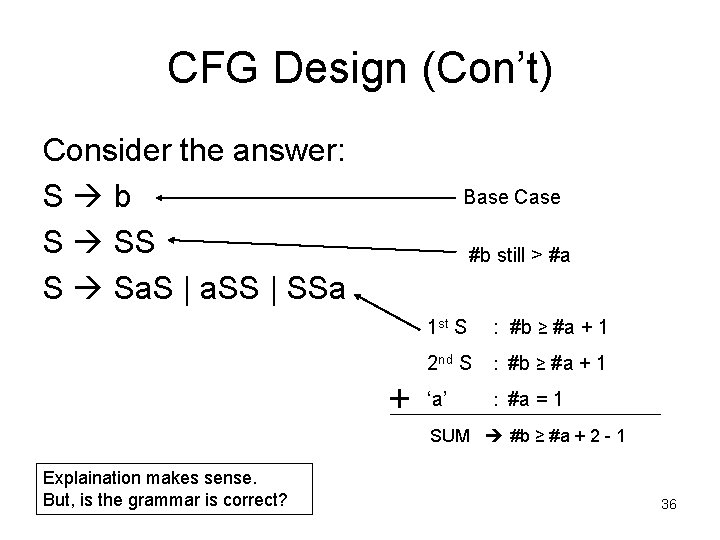
CFG Design (Con’t) Consider the answer: S b S SS S Sa. S | a. SS | SSa Base Case #b still > #a 1 st S : #b ≥ #a + 1 2 nd S : #b ≥ #a + 1 ‘a’ : #a = 1 SUM #b ≥ #a + 2 - 1 Explaination makes sense. But, is the grammar is correct? 36

CFG Design (Con’t) • After designing the grammar, G, you may have to prove (if required) that the language of this grammar is equivalent to the given language • i. e. , Prove that L(G) = L • Proof: A set of strings Part 1) L(G) ⊂ L Part 2) L ⊂ L(G) • Due to time limit, I will not do this part 37

Parse Tree • How to parse “aab” in this grammar? (Previous example) CFG Example Derivation S AB | ba S AB A a. A | a a. AB B b aa. B aab 38

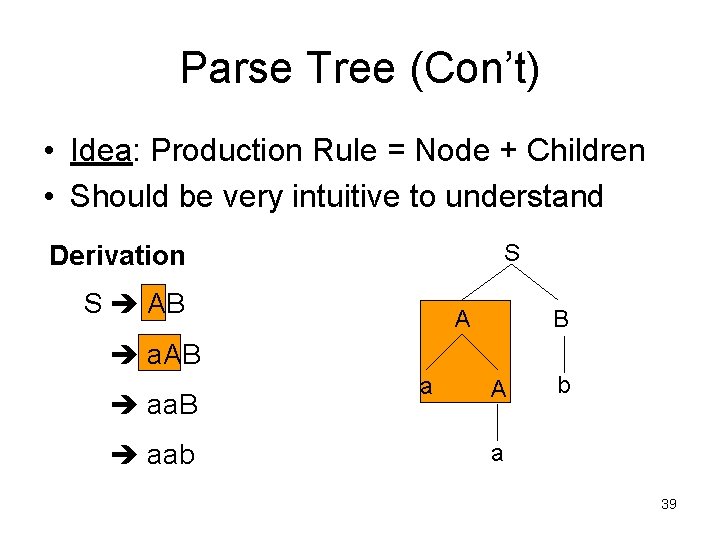
Parse Tree (Con’t) • Idea: Production Rule = Node + Children • Should be very intuitive to understand S Derivation S AB A B a. AB aab a A b a 39

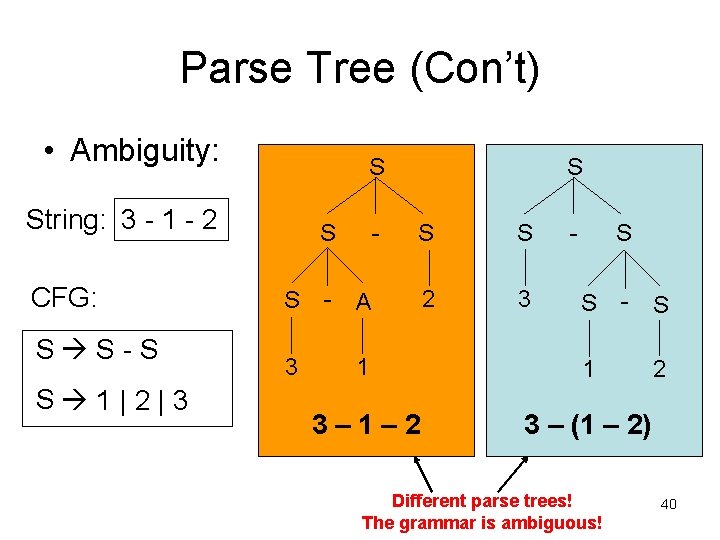
Parse Tree (Con’t) • Ambiguity: String: 3 - 1 - 2 CFG: S S-S S 1|2|3 S S 3 - - S S 2 3 A - S S - 1 1 3– 1– 2 3 – (1 – 2) Different parse trees! The grammar is ambiguous! S 2 40

Parse Tree (Con’t) • Useful in programming language – CSC 3180 • Useful in compiler – CSC 3120 41

End • Thanks for coming! • Any questions? 42