Tutorial 02 CSC 3130 Formal Languages and Automata

Tutorial 02 -- CSC 3130 : Formal Languages and Automata Theory Tu Shikui (sktu@cse. cuhk. edu. hk) SHB 905, Office hour: Thursday 2: 30 pm-3: 30 pm 2008 -09 -12

Outline n From NFA to NFA n From DFA to RE n Closed operators for Regular Languages

From NFA to NFA n -transitions n n is the empty string, “it contains no alphabets”; It makes a state transition when seeing . It makes a state transition without receiving an input symbol (from alphabet); It makes a state transition unconditionally; n NFA n n n NFA + Allows -transitions; It brings “programming convenience”; Closely related to regular expressions

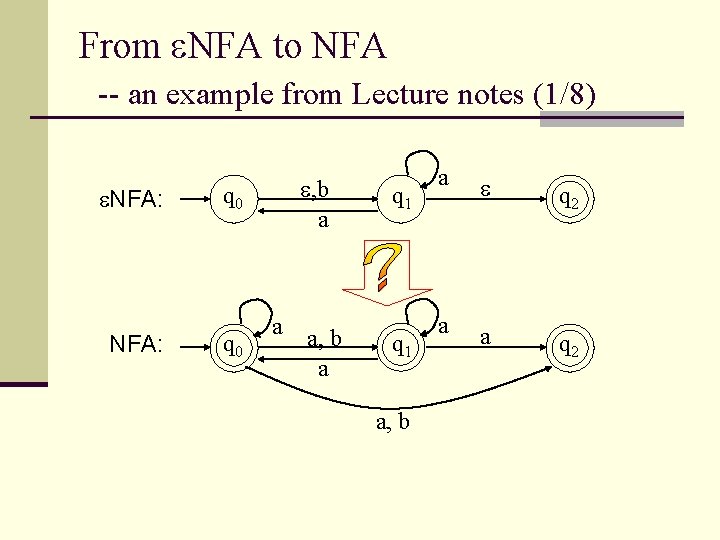
From NFA to NFA -- an example from Lecture notes (1/8) NFA: , b a q 0 a a, b a q 1 a, b a q 2 a a q 2

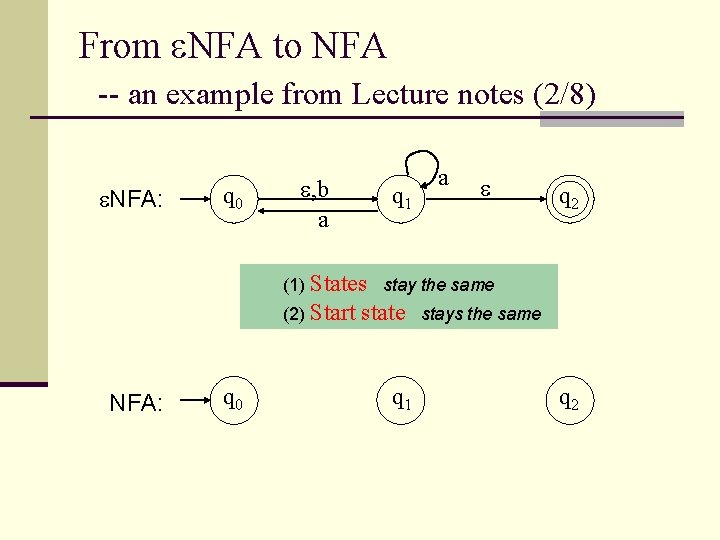
From NFA to NFA -- an example from Lecture notes (2/8) NFA: q 0 , b a q 1 a q 2 (1) States stay the same (2) Start NFA: q 0 state q 1 stays the same q 2

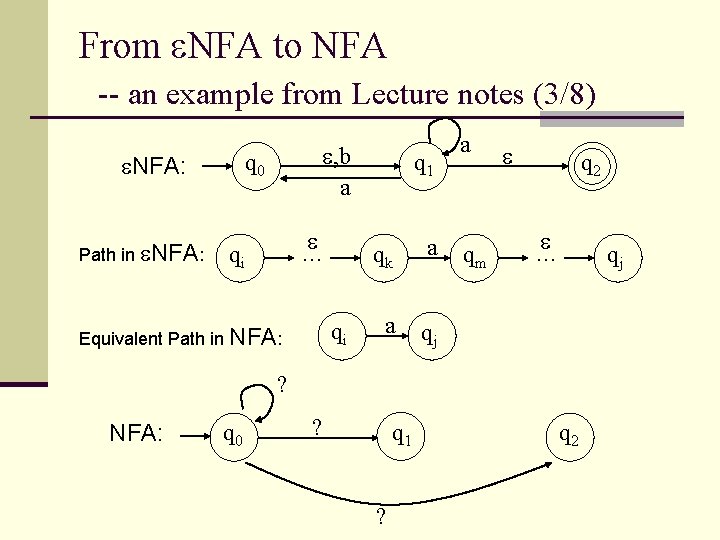
From NFA to NFA -- an example from Lecture notes (3/8) q 0 NFA: Path in NFA: , b a … qi qi Equivalent Path in NFA: q 1 qk a a qj a qm q 2 … qj ? NFA: q 0 ? q 1 ? q 2

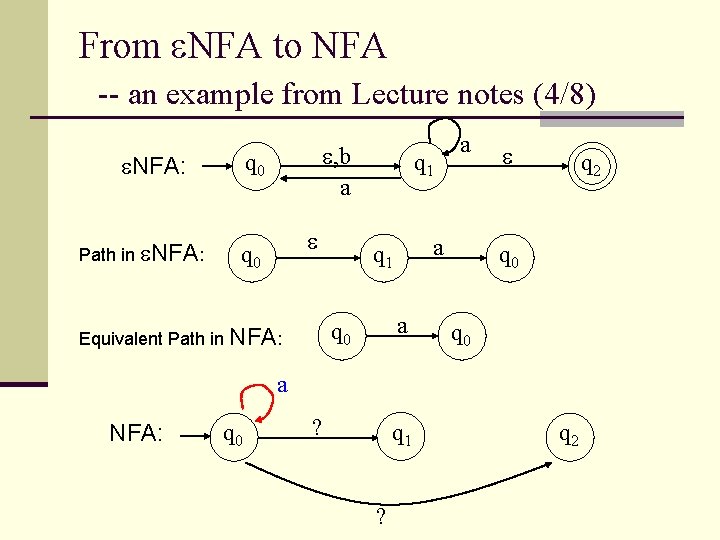
From NFA to NFA -- an example from Lecture notes (4/8) q 0 NFA: Path in NFA: , b a q 0 q 1 a q 0 Equivalent Path in NFA: a q 2 q 0 a NFA: q 0 ? q 1 ? q 2

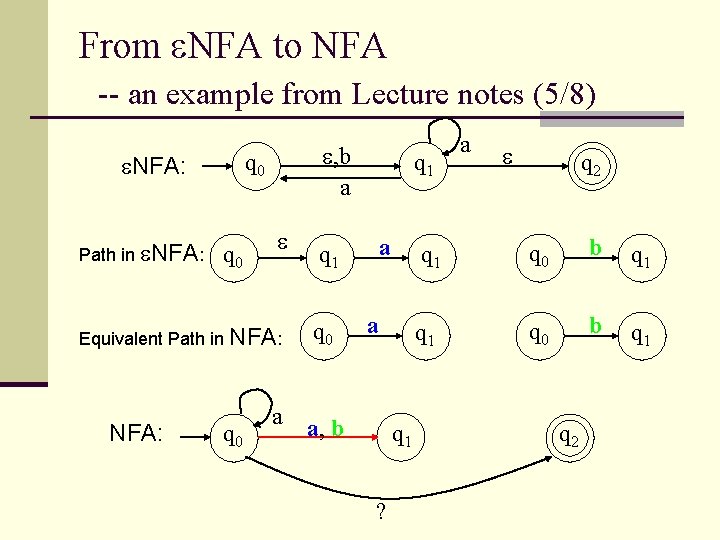
From NFA to NFA -- an example from Lecture notes (5/8) q 0 NFA: Path in NFA: , b a q 0 Equivalent Path in NFA: q 0 a q 1 q 0 q 1 a a a, b q 1 ? a q 2 q 1 q 0 b q 1 q 2

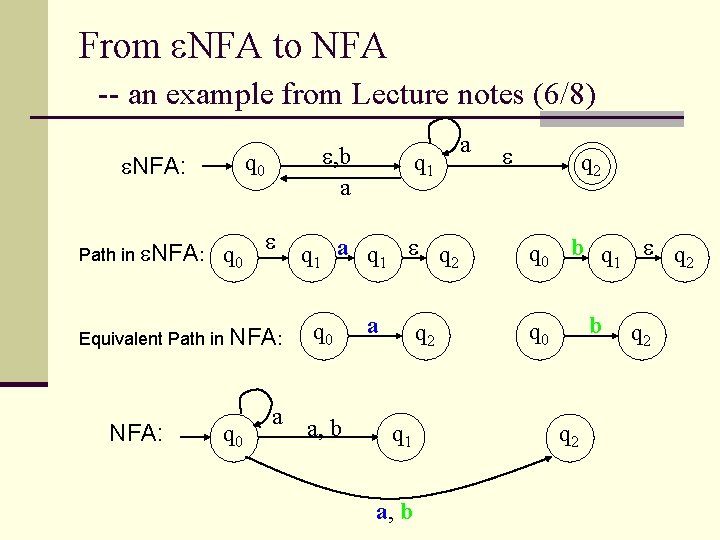
From NFA to NFA -- an example from Lecture notes (6/8) q 0 NFA: Path in NFA: , b a q 0 Equivalent Path in NFA: q 0 a q 1 q 2 q 0 a, b a q 2 q 1 a, b a q 2 q 0 b q 1 q 2 b q 0 q 2

From NFA to NFA -- an example from Lecture notes (7/8) NFA: , b a q 0 a a, b a q 1 a, b a q 2 a a q 2

From NFA to NFA -- an example from Lecture notes (8/8) NFA: , b a q 0 q 1 a q 2 (4) The accepting states of the NFA are all states that can reach some accepting state of NFA using only -transitions NFA: q 0 a a, b a q 1 a, b a a q 2

Outline n From NFA to NFA n From DFA to RE n Closed operators for Regular Languages

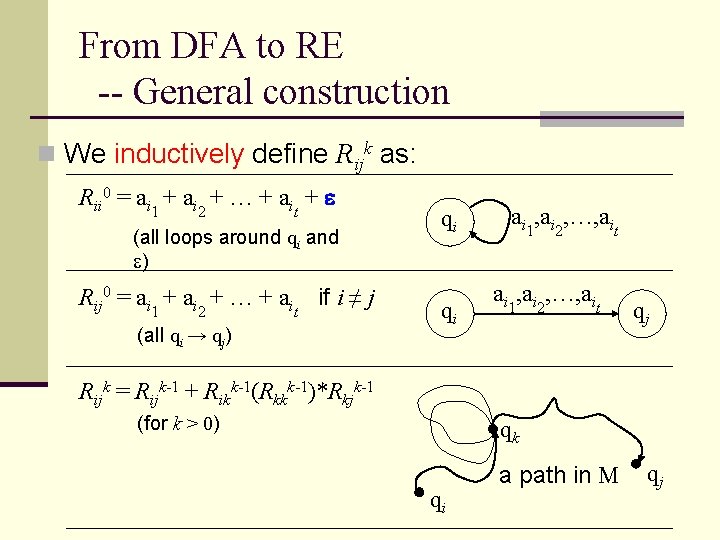
From DFA to RE -- General construction n We inductively define Rijk as: Rii 0 = ai 1 + ai 2 + … + ait + e (all loops around qi and ) Rij 0 = ai + … + ai 1 2 t if i ≠ j (all qi → qj) qi qi ai 1, ai 2, …, ait qj Rijk = Rijk-1 + Rikk-1(Rkkk-1)*Rkjk-1 (for k > 0) qk qi a path in M qj

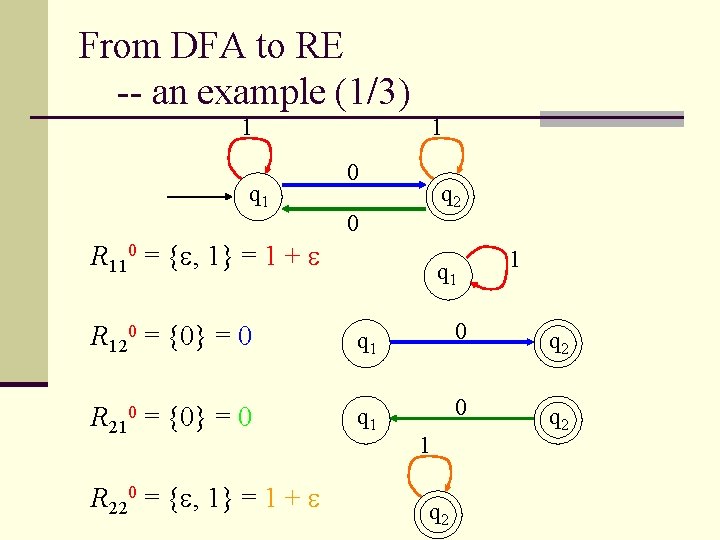
From DFA to RE -- an example (1/3) 1 q 1 1 0 q 2 0 R 110 = { , 1} = 1 + q 1 1 R 120 = {0} = 0 q 1 0 q 2 R 210 = {0} = 0 q 1 0 q 2 R 220 = { , 1} = 1 + 1 q 2

From DFA to RE Rijk = Rijk-1 + Rikk-1(Rkkk-1)*Rkjk-1 -- an example (2/3) 1 q 1 1 0 0 q 2 R 110 = { , 1} = 1 + ; R 210 = {0} = 0; R 111 = { , 1, 111, . . . } R 120 = {0} = 0 = 1* R 220 = { , 1} = 1 + 1 = R 0 + R 0(R 0)*R 0 1 0 0 R R 12 = R 12 + R 11 (R 11 )*R 12 22 22 21 11 12 = (1 + ) + 0(1+ )*0 = 0 + (1+ )+0 R 122 = R 121 + R 121(R 221)*R 221 = (0 + (1+ )+0) + (0 + (1+ )+0) ((1 + ) + 0(1+ )*0)+ = (0 + (1+ )+0) ((1 + ) + 0(1+ )*0)* = (1+ )*0 ((1 + ) + 01*0)* = 1*0 (1 + 01*0)*

From DFA to RE (3/3) -- Determine the accepted RE for DFA n Suppose the DFA start state is q 1, and the accepting states are F = {qj 1 qj 2 … qjt} n Then the regular expression for this DFA is R 1 j n + …. . + R 1 j n 1 1 q 1 2 t 1 0 0 q 2 R 122=1*0 (1+01*0)*

Outline n From NFA to NFA n From DFA to RE n Closed operators for Regular Languages

Closed operators for Regular Languages -- An Exercise n Prove or disprove the regular languages are closed under the following operations: (1). min(L) = { w | w is in L, but no proper prefix of w is in L }; n (2). max(L) = { w | w is in L and for no x other than εis wx in L }; n (3). init(L) = { w | for some x, wx is in L } n Hint: Start with a DFA for L and perform a construction to get the desired language.

(1). min(L) = { w | w is in L, but no proper prefix of w is in L }; What is “proper prefix”? For example, suppose the alphabet is { 0, 1 }, then: (1) “ 011”, “ 01” are proper prefixes of “ 0110001”; (2) “ 0110001” is a prefix of “ 0110001”, but not a proper prefix; (3) “” (i. e. , ε) is not a proper prefix of “ 0110001”.

(1). min(L) = { w | w is in L, but no proper prefix of w is in L }; What does min(L) look like? Example(1). L = { 00, 0011, 101 }; min(L) = ? { 00, 0011, 101 } 0 1 0 1 Main idea: Example(2). n, m = 0, 1, 2, … L = { a, a(bc)n, baa, cbma }; min(L) =? 1 w=ux A DFA for L: q 0 u qj x qk Cut the transitions going out of each accepting state.

Solution for (1) min(L) = { w | w is in L, but no proper prefix of w is in L };

Solution for (1) -- (cont. ) min(L) = { w | w is in L, but no proper prefix of w is in L };

Properties of Regular Languages -- An Exercise n Prove or disprove the regular languages are closed under the following operations: (1). min(L) = { w | w is in L, but no proper prefix of w is in L }; n (2). max(L) = { w | w is in L and for no x other than εis wx in L }; n (3). init(L) = { w | for some x, wx is in L } n Hint: Start with a DFA for L and perform a construction to get the desired language. Left as exercises at home!

End of this tutorial! Thanks for coming!