Tutorial 11 CSC 3130 Formal Languages and Automata








- Slides: 12

Tutorial 11 -- CSC 3130 : Formal Languages and Automata Theory Tu Shikui (sktu@cse. cuhk. edu. hk) SHB 905, Office hour: Thursday 2: 30 pm-3: 30 pm 2008 -11 -16

Outline n Examples for n Decidable n Undecidable but Recognizable n Unrecognizable

The difference -- between Recognizable and decidable n If L is decidable, then L is recognized by a TM M that halts on all inputs. Note that, L might be recognized by other TM M’ that does not always halt. n If L is recognizable, then there might be such TM M that recognizes L but run forever, rather than rejecting, some inputs not in L. n Simply, Decidable ---- always halt Recognizable ---- halt or loop

Example 1 -- Is it decidable? The shaded area: Proof: Decidable. Construct a TM M as follows: L(A) L(B)

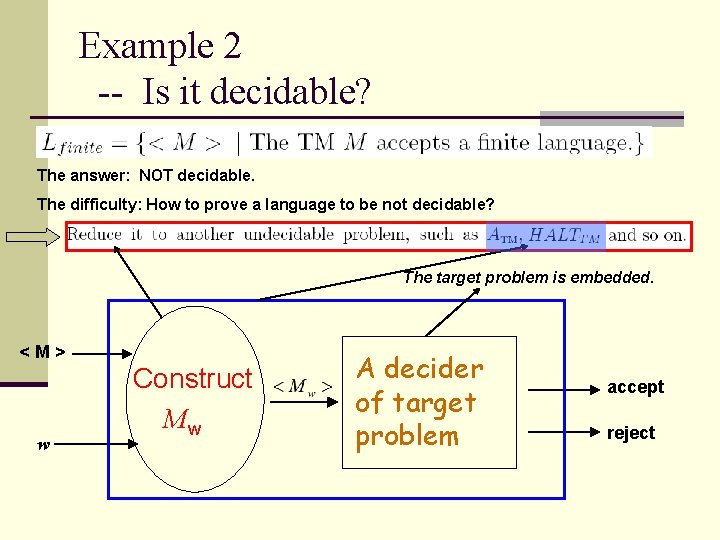
Example 2 -- Is it decidable? The answer: NOT decidable. The difficulty: How to prove a language to be not decidable? The target problem is embedded. <M> w Construct Mw A decider of target problem accept reject

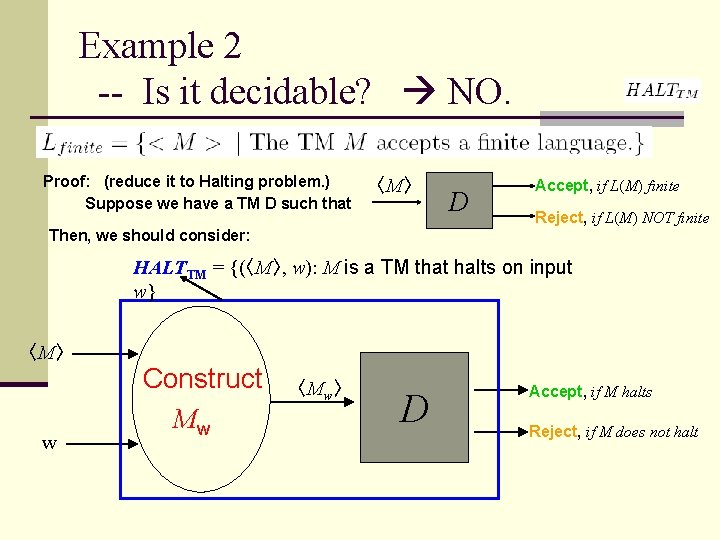
Example 2 -- Is it decidable? NO. Proof: (reduce it to Halting problem. ) Suppose we have a TM D such that 〈M〉 D Accept, if L(M) finite Reject, if L(M) NOT finite Then, we should consider: HALTTM = {(〈M〉, w): M is a TM that halts on input w} 〈M〉 w Construct Mw 〈Mw〉 D Accept, if M halts Reject, if M does not halt

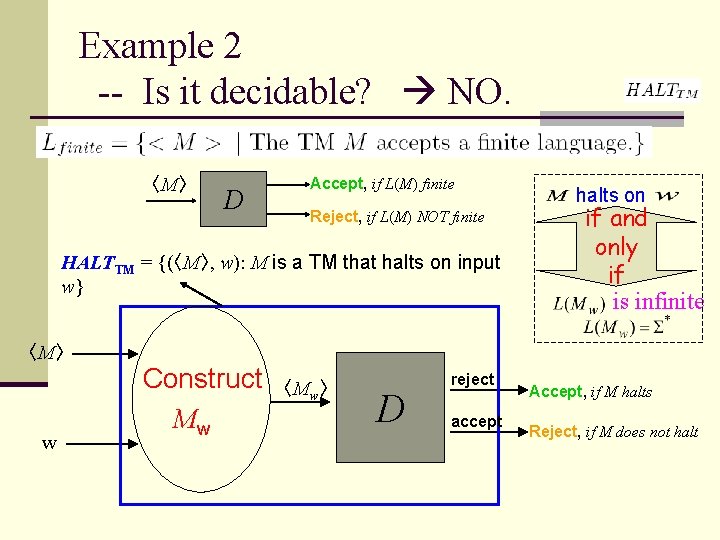
How to construct Mw ? Our Target … halts on if and only if is infinite Construction On any input string: s Simulate M on w ; If M halts, accept s, else reject s, end

Example 2 -- Is it decidable? NO. 〈M〉 D Accept, if L(M) finite Reject, if L(M) NOT finite HALTTM = {(〈M〉, w): M is a TM that halts on input w} halts on if and only if is infinite 〈M〉 w Construct Mw 〈Mw〉 D reject accept Accept, if M halts Reject, if M does not halt

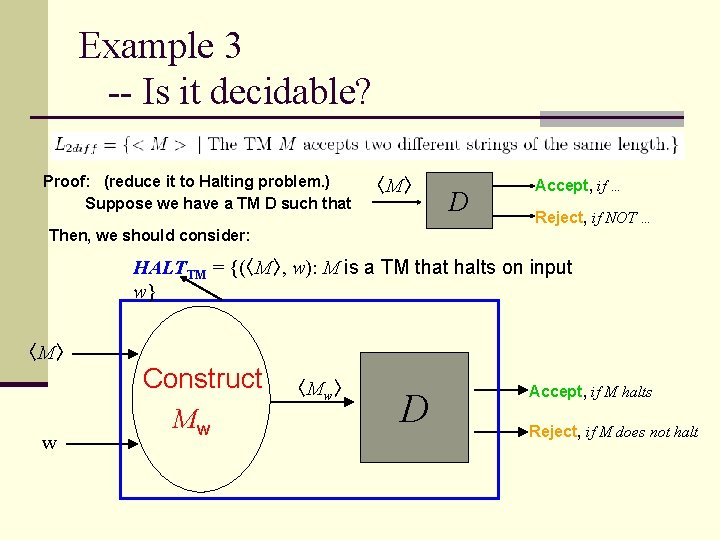
Example 3 -- Is it decidable? Proof: (reduce it to Halting problem. ) Suppose we have a TM D such that 〈M〉 D Accept, if … Reject, if NOT … Then, we should consider: HALTTM = {(〈M〉, w): M is a TM that halts on input w} 〈M〉 w Construct Mw 〈Mw〉 D Accept, if M halts Reject, if M does not halt

How to construct Mw ? Our Target … halts on if and only if Contains two equal length strings Construction On any input string: s Simulate M on w ; If M halts, accept if s=a or s=b else reject s, end

Example 4 -- Is it decidable? Proof: Suppose we have a TM D such that 〈M〉 D Accept, if … Reject, if NOT … ATM = {(〈M〉, w): M is a TM that accepts w} 〈M〉 w Construct Mw 〈Mw〉 D Accept, if M accept w Reject, if not

End of this tutorial! Thanks for coming!