CSCI 3130 Formal languages and automata theory Tutorial

CSCI 3130: Formal languages and automata theory Tutorial 5 Chin

Reminder • Homework 3 is due tomorrow. • Midterm is on next Monday. • Review session tomorrow. • You can get back homework 2 after this tutorial.

Homework 2 • We only say a language is regular or non-regular. • We do not say a string is regular or non-regular • Never write x is regular • We only say a string is in a language or not.

Homework 2 • To show a language is not regular (a) You only have to choose one string. (b) The chosen string should be in terms of n. (c) You cannot choose what u, v, w are. e. g. u = (ab)n-1, v = (ab)n, w = (bc)n. wrong! You have to consider every possible partitions of uvw. (d) You only have to choose one value for i.

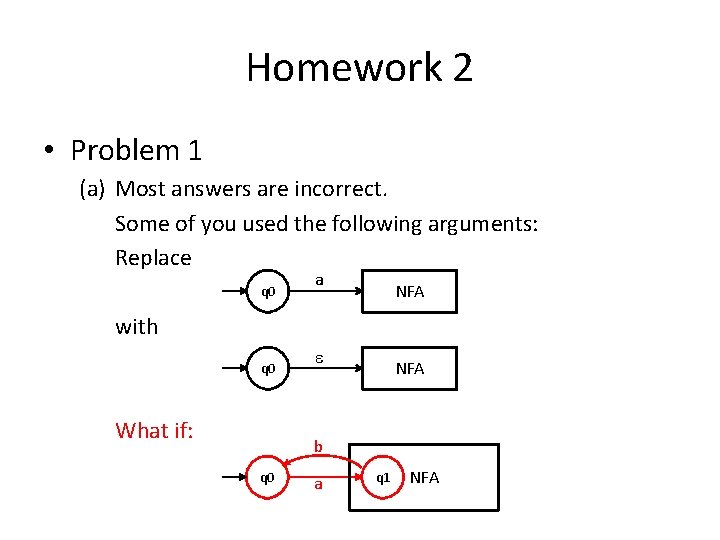
Homework 2 • Problem 1 (a) Most answers are incorrect. Some of you used the following arguments: Replace q 0 a NFA with q 0 What if: NFA b q 0 a q 1 NFA

Homework 2 • Problem 1 (a) There can be multiple accepting states in the DFA Many states can reach an accepting state on ‘b’

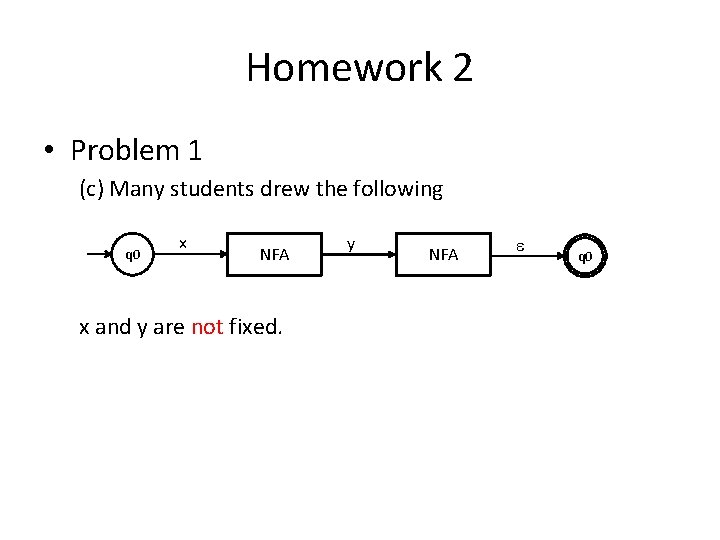
Homework 2 • Problem 1 (c) Many students drew the following q 0 x NFA x and y are not fixed. y NFA q 0

Homework 2 • Problem 1 (d) A few students did the following Let L 1 = {anb: n ≥ 0}, L 2 = {an: n ≥ 0} Then L 1 L 2 = {anban : n ≥ 0}. wrong! The n in L 1 and the n in L 2 are independent. L 1 L 2 = {anbam : n, m ≥ 0}.

Homework 2 • Problem 2 (a) Some of you chose the strings (a+b)n(b+c)n The proof fails if I take bnbn, which is of the above form. Choose one string is okay. e. g. ancn

Homework 2 • Problem 2 (c) L 3 = {w : w does not have the same number of as, bs, and cs} A few students got L 3 wrong. (b) Many students let u = (ac)n-1, v = (ac), w = (abc)n. You cannot choose what u, v, w are! v can be any nonempty substring of the first n characters of the string. e. g. v can be the first ‘a’ of the string.

Homework 2 • Problem 3 (b) To show two states are distinguishable Write down on what inputs one of them goes to an accepting state but the other does not.

Homework 2 • Problem 4 (b) Some of you did not handle names without any ‘a’. (c) A few of you did not handle the names “crystal”. (d) A few of you missed the case “rin”.

Pushdown Automata • NFA with a stack q 0 • • a, b/c q 1 Read a, pop b, and push c Push c to the stack after popping b a, b, c can be Use $ to mark stack bottom

Pushdown Automata • PDA = CFG • Languages that can be represented by PDA/CFG are context-free.

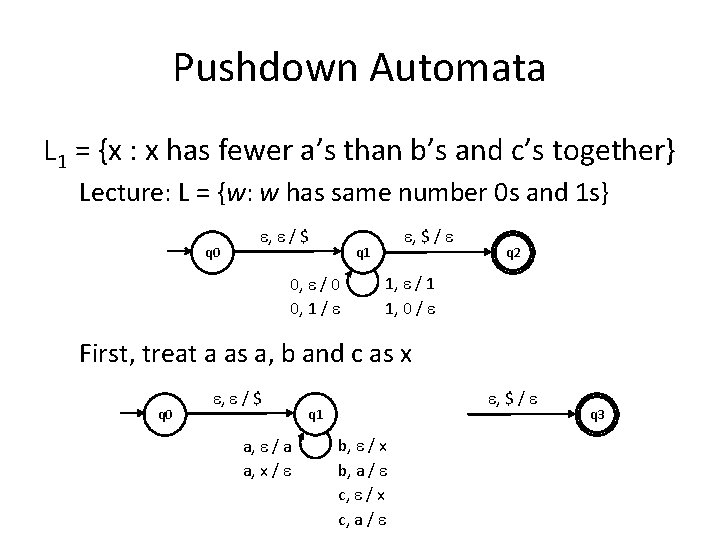
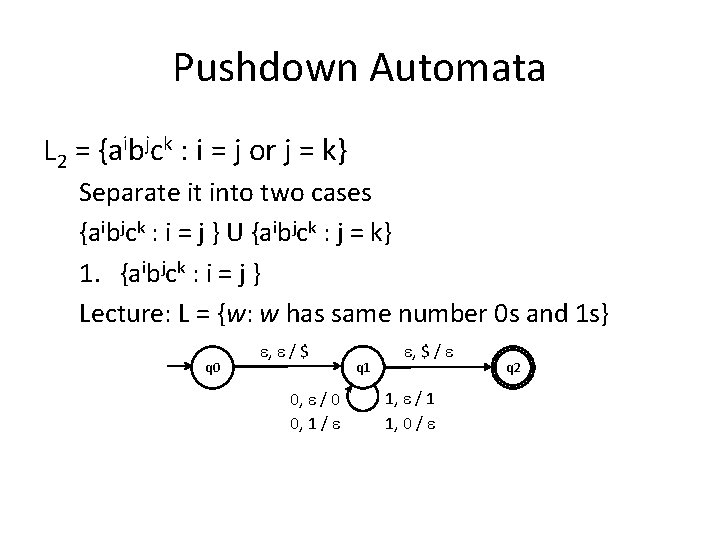
Pushdown Automata • Design a PDA for the following. S = {a, b, c} L 1 = {x : x has fewer a’s than b’s and c’s together} L 2 = {aibjck : i = j or j = k}

Pushdown Automata L 1 = {x : x has fewer a’s than b’s and c’s together} Lecture: L = {w: w has same number 0 s and 1 s} q 0 , / $ , $ / q 1 0, / 0 0, 1 / q 2 1, / 1 1, 0 / First, treat a as a, b and c as x q 0 , / $ a, / a a, x / , $ / q 1 b, / x b, a / c, / x c, a / q 3

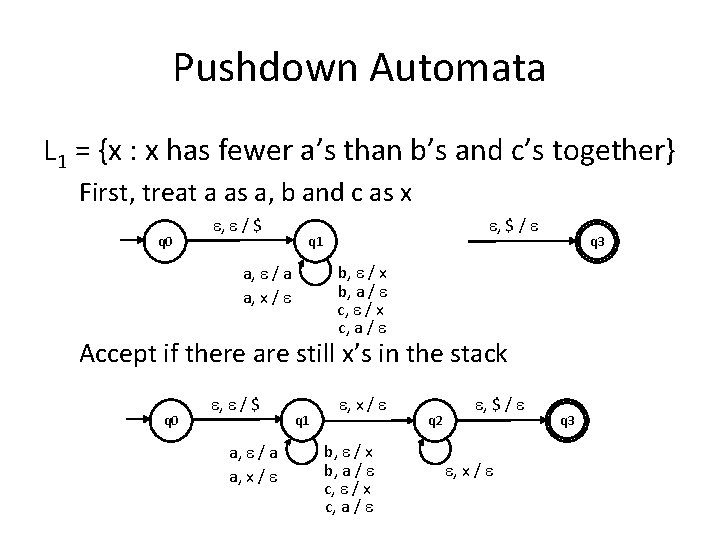
Pushdown Automata L 1 = {x : x has fewer a’s than b’s and c’s together} First, treat a as a, b and c as x q 0 , / $ , $ / q 1 q 3 b, / x b, a / c, / x c, a / a, / a a, x / Accept if there are still x’s in the stack q 0 , / $ a, / a a, x / q 1 , x / b, / x b, a / c, / x c, a / q 2 , $ / , x / q 3

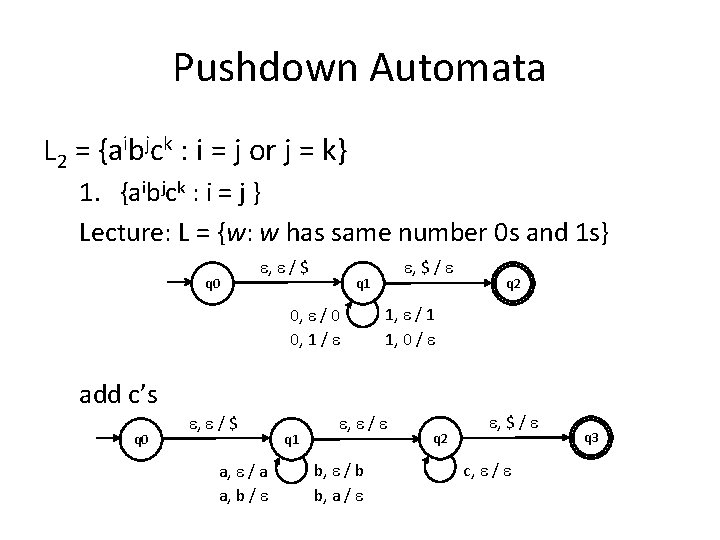
Pushdown Automata L 2 = {aibjck : i = j or j = k} Separate it into two cases {aibjck : i = j } U {aibjck : j = k} 1. {aibjck : i = j } Lecture: L = {w: w has same number 0 s and 1 s} q 0 , / $ 0, / 0 0, 1 / q 1 , $ / 1, / 1 1, 0 / q 2

Pushdown Automata L 2 = {aibjck : i = j or j = k} 1. {aibjck : i = j } Lecture: L = {w: w has same number 0 s and 1 s} q 0 , / $ , $ / q 1 0, / 0 0, 1 / q 2 1, / 1 1, 0 / add c’s q 0 , / $ a, / a a, b / q 1 , / b, / b b, a / q 2 , $ / c, / q 3

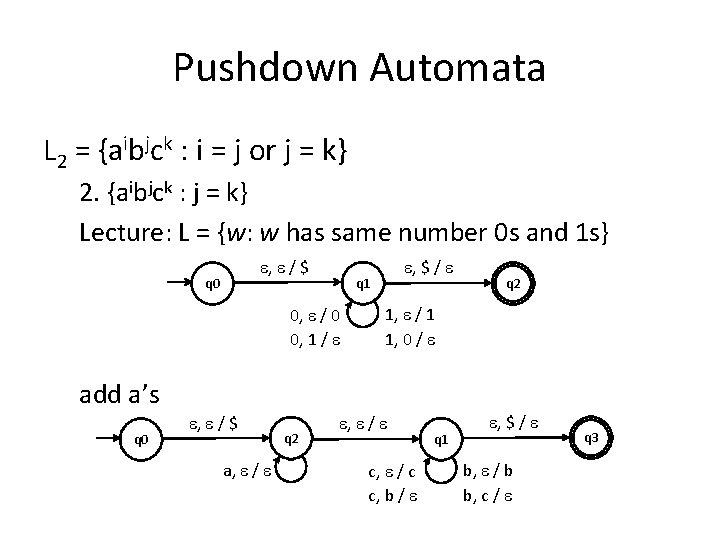
Pushdown Automata L 2 = {aibjck : i = j or j = k} 2. {aibjck : j = k} Lecture: L = {w: w has same number 0 s and 1 s} , / $ q 0 , $ / q 1 0, / 0 0, 1 / q 2 1, / 1 1, 0 / add a’s q 0 , / $ a, / q 2 , / c, / c c, b / q 1 , $ / b, / b b, c / q 3

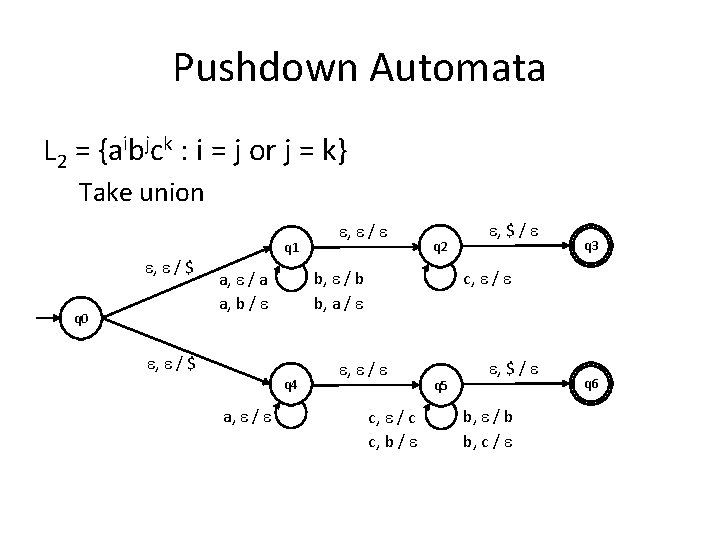
Pushdown Automata L 2 = {aibjck : i = j or j = k} Take union , / $ q 0 q 1 q 2 b, / b b, a / a, / a a, b / , / $ q 4 a, / , $ / q 3 c, / c c, b / q 5 , $ / b, / b b, c / q 6

Pumping lemma for Context-free languages To show a language L is not context free: For every n, choose one z of length ≥ n in L, such that for every way of writing z = uvwxy where |vwx| ≤ n and |vx| ≥ 1, the string uviwxiy is not in L for some i ≥ 0. 1. z depends on n 2. u, w, y can be empty string 3. v, x can also be empty string, but not both. 4. i can be 0 (very useful) 5. You only have to choose one z 6. Unlike the regular language version, vwx can be anywhere in z.

Pumping lemma for Context-free languages Template Suppose L is context-free. Let n be the pumping length. Then z = _______ (z should contain n somewhere) is in L. Write z = uvwxy, where |vwx| ≤ n and |vx|≥ 1. Argue! no matter how we write z = uvwxy, the string uv_wx_y is not in L (choose one i in _, i can be 0) Therefore L is not regular.

Pumping lemma for CFG • Show that the following languages are not context-free L 1 = {anbm : m, n ≥ 0}. S = {a, b}. L 2 = {x#y#z : y. R is a substring of xz; x, y, z ∈ {a, b}*}. S = {a, b, #}.

Pumping lemma for CFG L 1 = {anbm : m, n ≥ 0}. S = {a, b}. Suppose L is context-free. Let n be the pumping length. Then z = _anbn_ (z should contain n somewhere) is in L. Write z = uvwxy, where |vwx| ≤ n and |vx|≥ 1. Argue! no matter how we write z = uvwxy, the string uv_wx_y is not in L (choose one i in _, i can be 0) How to argue?

Pumping lemma for CFG L 1 = {anbm : m, n ≥ 0}. S = {a, b}. Then z = _anbn_ (z should contain n somewhere) is in L. Write z = uvwxy, where |vwx| ≤ n and |vx|≥ 1. What can vwx be if |vwx| ≤ n? vwx can be… 1. part of the first an 2. part of the first anbn a……ab……b 3. part of the first bn 4. part of the middle bnan 5. part of the second an 6. part of the second anbn 7. part of the last bn

Pumping lemma for CFG L 1 = {anbm : m, n ≥ 0}. S = {a, b}. Then z = _anbn_ (z should contain n somewhere) is in L. Write z = uvwxy, where |vwx| ≤ n and |vx|≥ 1. 1. If vwx is part of the first an uv 2 wx 2 y has less a’s in the first group than the second group 2. If vwx is part of the first anbn v and x cannot be both empty a……ab……b If v is not empty, v must contain some a, uv 0 wx 0 y has less a’s in the first group than the second group If x is not empty, x must contain some b, uv 0 wx 0 y has less b’s in the first group than the second group The rest are similar, do explain them in the homework/exam.

Pumping lemma for CFG L 2 = {x#y#z : y. R is a substring of xz; x, y, z ∈ {a, b}*}. Suppose L is context-free. Let n be the pumping length. Then z = _an#bn_ (z should contain n somewhere) is in L. Write z = uvwxy, where |vwx| ≤ n and |vx|≥ 1. Argue! no matter how we write z = uvwxy, the string uv_wx_y is not in L (choose one i in _, i can be 0) How to argue?

Pumping lemma for CFG L 2 = {x#y#z : y. R is a substring of xz; x, y, z ∈ {a, b}*}. Then z = _an#bn_ (z should contain n somewhere) is in L. Write z = uvwxy, where |vwx| ≤ n and |vx|≥ 1. What can vwx be if |vwx| ≤ n? vwx can be… 0. If v and x contain ‘#’, then we can always pump it and the string will contain more than 2 #s. 1. 2. 3. 4. 5. 6. 7. part of the first an#bn part of the first bn part of the middle bnan part of the second an vwx is part of the last an#bn vwx is part of the last bn a……a#b……b

Pumping lemma for CFG L 2 = {x#y#z : y. R is a substring of xz; x, y, z ∈ {a, b}*}. Then z = _an#bn_ (z should contain n somewhere) is in L. Write z = uvwxy, where |vwx| ≤ n and |vx|≥ 1. 0. If v and x contain ‘#’, then we can always pump it and the string will contain more than 2 #s, which is not in L 2. a……a#b……b n 1. If vwx is part of the first a , uv 0 wx 0 y = X#Y#Z contains less a’s in X than in Y. thus the YR cannot be a substring of XZ.

Pumping lemma for CFG L 2 = {x#y#z : y. R is a substring of xz; x, y, z ∈ {a, b}*}. Then z = _an#bn_ (z should contain n somewhere) is in L. Write z = uvwxy, where |vwx| ≤ n and |vx|≥ 1. 0. If v and x contain ‘#’, then we can always pump it and the string will contain more than 2 #s, which is not in L 2. 2. If vwx is part of the first an#bn, a……a#b……b v and x cannot be both empty If v is not empty, v must contain some a, uv 0 wx 0 y = X#Y#Z contains less a’s in X than in Y. thus the YR cannot be a substring of XZ. If x is not empty, x must contain some b, uv 2 wx 2 y = X#Y#Z contains less b’s in X than in Y. thus the YR cannot be a substring of XZ. The rest are similar, do explain them in the homework/exam.

End • Questions?