Deterministic Finite Automata CS 130 Theory of Computation

Deterministic Finite Automata CS 130: Theory of Computation HMU textbook, Chapter 2 (Sec 2. 2)

State-driven programs n Many applications carry out actions only when particular conditions apply at the given moment n n conditions => state Examples: n n Buying items online: a payment can be made only after checkout Performing a simple arithmetic calculation using a calculator: an operator character should be pressed only after some sequence of digits have been entered for the first operand

Model: finite automaton n n At any point in time, the “program” or automaton will be in one state from a set of states In the calculator example, the states are: n n n reading the first operand read (+ or - is pressed) reading the second operand result displayed/ready for next calculation (= is pressed) A transition from one state to another state occurs on a given input symbol

Accepting valid calculator input n We want the automaton to allow (accept) input strings like this n n n But “reject” string like this n n n 123+456= 3333 -5= +-2=2 567 -= Symbols are read from left to right and cause transitions from one state to another based on the current state and current input symbol

Deterministic Finite Automata n A DFA or deterministic finite automaton M is a 5 -tuple, M = (Q, , , q 0, F), where: n n n Q is a finite set of states of M is the finite input alphabet of M : Q Q is the state transition function q 0 is the start state of M F Q is the set of accepting states or final states of M

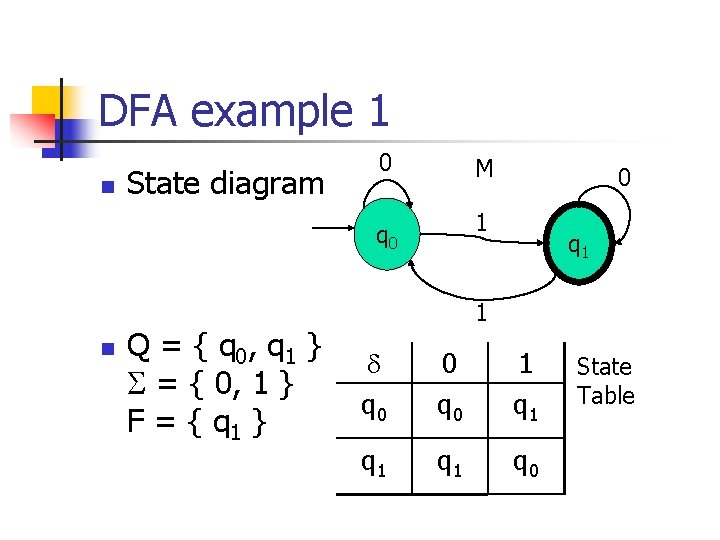
DFA example 1 n State diagram 0 M 1 q 0 n Q = { q 0, q 1 } = { 0, 1 } F = { q 1 } 0 q 1 1 q 0 0 q 0 1 q 1 q 0 State Table

State table & state transition function n n State table q 0 0 q 0 1 q 1 q 0 State transition function (q 0, 0) = q 0, (q 0, 1) = q 1 (q 1, 0) = q 1, (q 1, 1) = q 0

A DFA processing a string n n Given a string of input symbols w = a 1 a 2 … a n A DFA M processes the string w as follows: n n n Start with state qx = q 0 For each input symbol ai : qx = (qx, ai) If resulting qx F, then w is accepted; otherwise w is rejected

Extending for strings n n Let w be a string over and let M = (Q, , , q 0, F) be a DFA Define ^: Q X * Q as follows n n n If w = , then ^(q, w) = ^(q, ) = q If w ≠ , i. e. , w = xa, (where x is a string and a is a symbol) then ^(q, w) = ^(q, xa) = ( ^(q, x), a) A DFA M accepts a string w when ^(q 0, w) F

Language recognized by a DFA n n n The language L(M) that is recognized by a DFA M = (Q, , , q 0, F), is the set of all strings accepted by M. That is, L(M) = { w * | M accepts w } = { w * | ^(q 0, w) F } Example: For the previous DFA, L(M) is the set of all strings of 0 s and 1 s with odd parity, that is, odd number of 1 s.

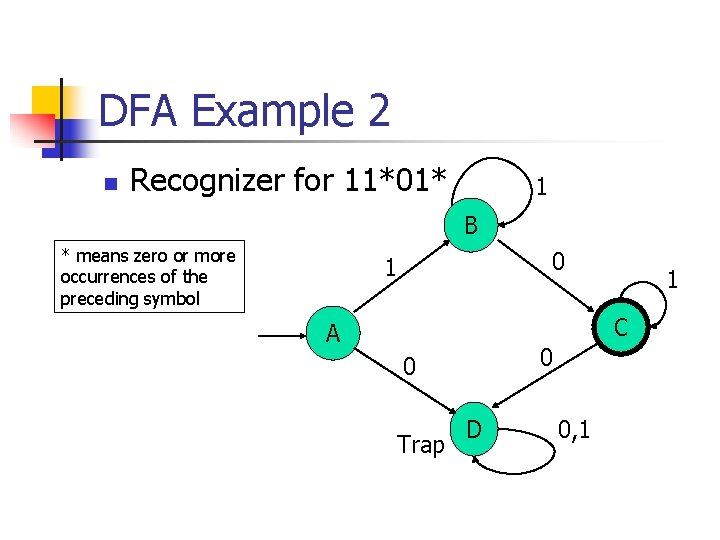
DFA Example 2 n Recognizer for 11*01* 1 B * means zero or more occurrences of the preceding symbol 0 1 1 C A 0 0 Trap D 0, 1

DFA Example 2 n M = (Q, , , q 0, F), L(M) = 11*01* Q = { q 0=A, B, C, D } = { 0, 1 } 0 1 F={C} A D B B C D C D D D

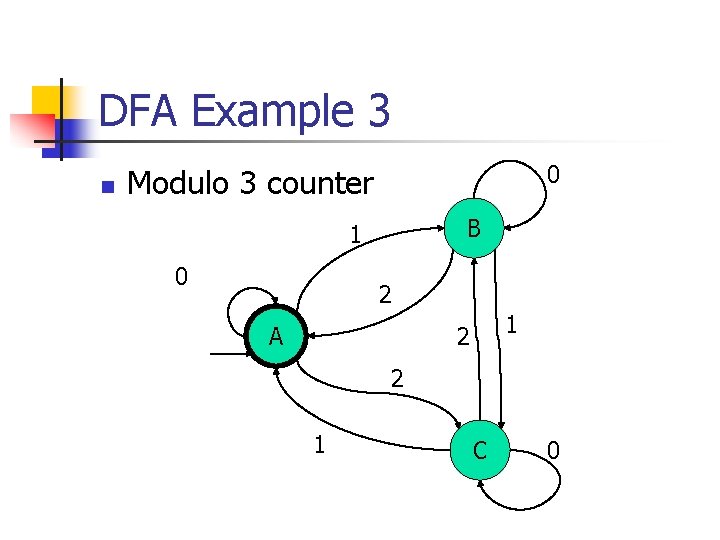
DFA Example 3 n 0 Modulo 3 counter B 1 0 2 A 1 2 2 1 C 0

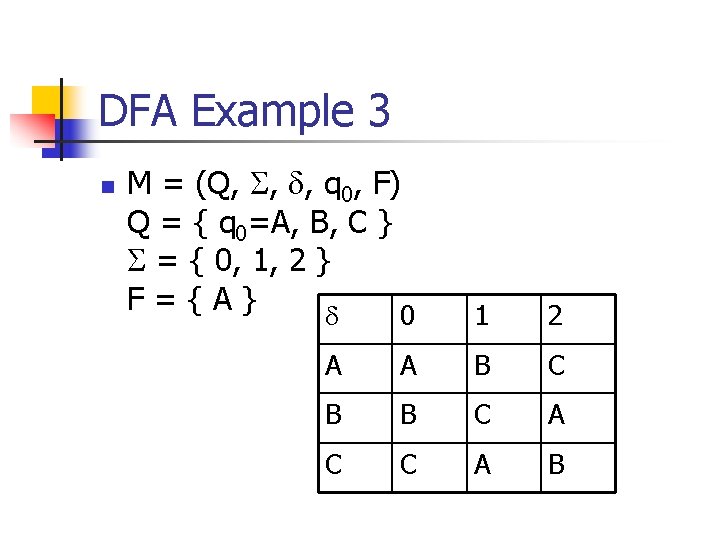
DFA Example 3 n M = (Q, , , q 0, F) Q = { q 0=A, B, C } = { 0, 1, 2 } F={A} 0 1 2 A A B C B B C A C C A B

DFA Example 4 n n n Recognizing simple calculator expressions M = (Q, , , q 0, F) Q = { q 0=ready, readingop 1, op 1 read, readingop 2 } = { 0… 9, +, -, = } F = { ready } See course website for a sample Java program that simulates this DFA (study how the transition function is implemented)

Regular Languages and DFAs n n A language L * is called regular if there exists a DFA M such that L(M)=L Examples of regular languages n n Binary strings with odd parity Language described by 11*01* Strings that form integers divisible by 3 Simple calculator expressions

Next n Variations on Finite Automata (rest of Chapter 2) n n n Nondeterministic Finite Automata (NFAs) Equivalences of these variations with DFAs Regular expressions as an alternative model for regular languages (Chapter 3)