Introduction to the Theory of Computation John Paxton

Introduction to the Theory of Computation John Paxton Montana State University Summer 2003

Humor • A busload of politicians were driving down a country road when, all of a sudden, the bus ran off the road and crashed into a tree in an old farmer's field. The old farmer, after seeing what had happened, went over to investigate. He then proceeded to dig a hole to bury the politicians. A few days later the local sheriff came out, saw the crashed bus, and asked the old farmer where all the politicians had gone. The old farmer said he had buried them. The sheriff asked the old farmer, "Were they all dead? " The old farmer replied, "Well, some of them said they weren't, but you know how them politicians lie. "

1. 2 Nondeterminism • In a nondeterministic machine, several choices might exist at a given point instead of only one.

Example 2 0 q 2 0, e q 1 1

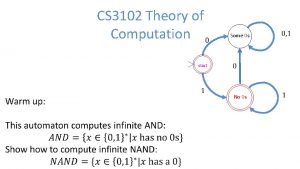
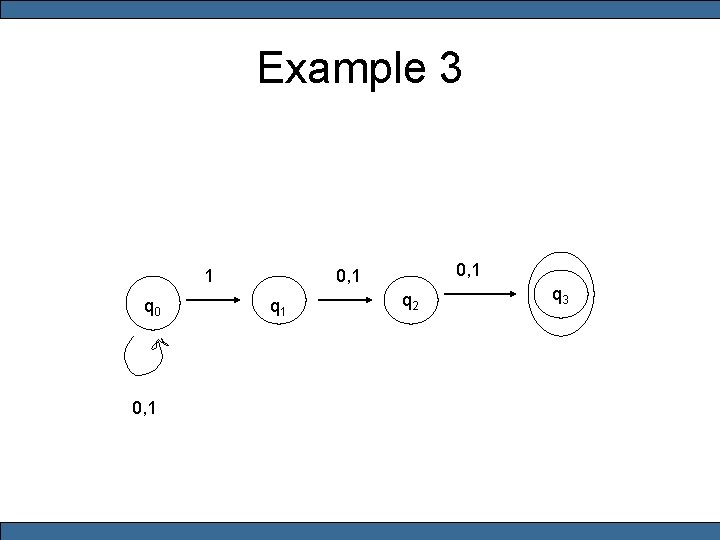
Example 3 • Write an NDFA that recognizes the language consisting of all strings over {0, 1} containing a 1 in the third position from the end.

Example 3 1 q 0 0, 1 q 2 q 3

Exercises • Give a 3 state NFA that accepts the language: zero or more 0 s, followed by zero or more ones, followed by zero or more 0 s followed by a 0. • Give a 1 state NFA that accepts the language {e}.

Formal Definition A nondeterministic finite automaton is a 5 tuple (Q, S, d, q 0, F) where 1. Q is a finite set called the states 2. S is a finite set called the alphabet 3. d : Q x Se P(Q) is the transition function 4. q 0 Î Q is the start state 5. F Í Q is the set of accept states

P(Q) • The power set of states • Consider Q = { q 0, q 1, q 2 } • Then P(Q) = { {}, {q 0}, {q 1}, {q 2}, {q 0, q 1}, {q 0, q 2}, {q 1, q 2}, {q 0, q 1, q 2} }

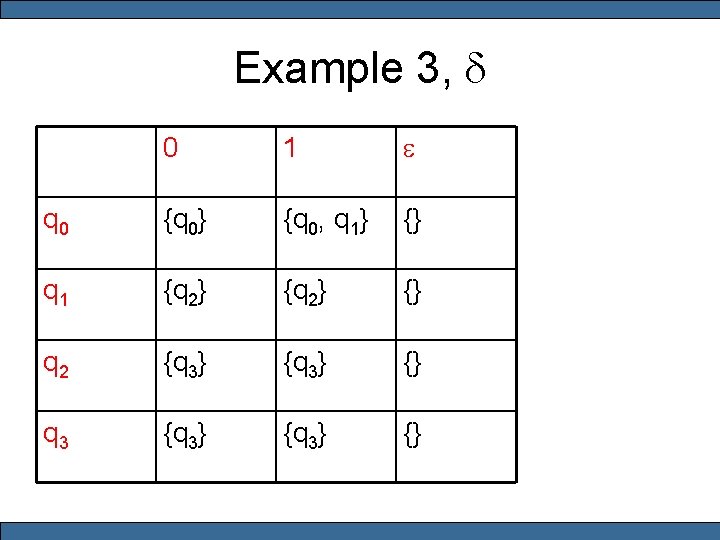
Example 3 • • Q = {q 0, q 1, q 2, q 3} S = {0, 1} q 0 F = {q 3}

Example 3, d 0 1 e q 0 {q 0} {q 0, q 1} {} q 1 {q 2} {} q 2 {q 3} {} q 3 {q 3} {}

Acceptance Let N = (Q, S, d, q 0, F) be an NFA and w = w 1 w 2 …wn be a string over the alphabet S. Then N “accepts” w if a sequence of states r 0 r 1…rn exists in Q with the following three conditions: 1. r 0 = q 0 2. ri+1 Î d(ri, wi+1) for 0 <= i <= n – 1 3. rn Î F

Theorem • Every nondeterministic finite automaton has an equivalent deterministic finite automaton.

Proof • Part 1 • Given a deterministic finite automaton, there is an equivalent nondeterministic finite automaton. • Proof. Trivial!

Proof • Part II. • Given a nondeterministic finite automaton, there is an equivalent deterministic finite automaton. • Proof. A bit harder …

Proof by Construction • Let N = (Q, S, d, q 0, F) • Construct M = (Q’, S, d’, q 0’, F’) • Q’ = P(Q) • q 0’ = E [ {q 0} ]

Proof by Construction • F’ = {R Î Q’ | R contains an accept state in N} • For R Î Q’ and a Î S, let d’(R, a) = {q Î Q | q Î E[d(r, a)] for some r Î R}

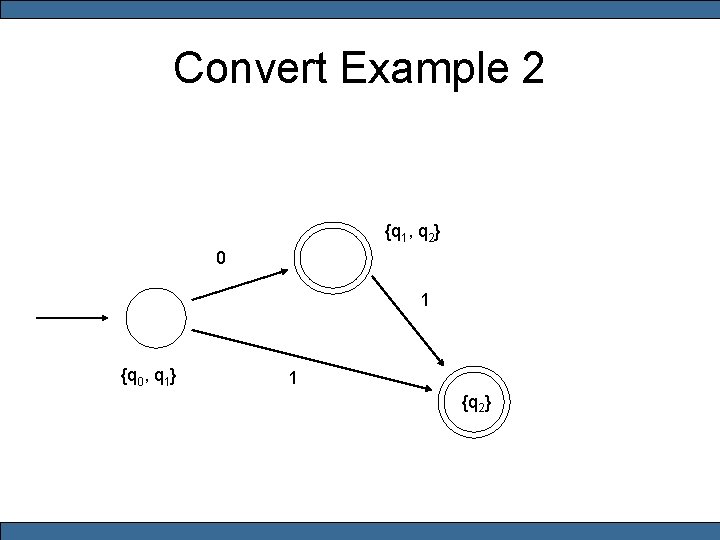
Convert Example 2 {q 1, q 2} 0 1 {q 0, q 1} 1 {q 2}

Exercise • Convert the following NFA into an equivalent DFA. e q 0 q 1 a a a, b q 2 b

Theorems • The class of regular languages is closed under the union operation. • The class of regular languages is closed under the concatenation operation. • The class of regular languages is closed under the star operation.

Closure Under Union • Note: we already proved this once using DFAs. • However, using NFAs, the proof is even easier so we will do it again!

Closure Under Union • Let N 1 = (Q 1, S, d 1, q 1, F 1) • Let N 2 = (Q 2, S, d 2, q 2, F 2) • Construct N = (Q, S, d, q 0, F) • Q = q 0 U Q 1 U Q 2

Closure Under Union • F = F 1 U F 2 • d(q, a) = d 1(q, a) if q Î Q 1 d 2(q, a) if q Î Q 2 {q 1, q 2} if q = q 0 and a = e {} if q = q 0 and a <> e

Exercises • Draw a picture that graphically displays how the preceding proof works. • Draw an NFA that accepts the union of {w | w begins with a 1 and ends with a 0} and {w | w contains at least three 1 s}

Closure Under Concatenation • Let N 1 = (Q 1, S, d 1, q 1, F 1) • Let N 2 = (Q 2, S, d 2, q 2, F 2) • Construct N = (Q, S, d, q 0, F) • Q = Q 1 U Q 2

Closure Under Concatenation • q 0 = q 1 • F = F 2 • d(q, a) = d 1(q, a) if q Î Q 1 and !(q Î F 1) d 1(q, a) if q Î F 1 and a <> e d 1(q, a) U {q 2} if q Î F 1 and a = e d 2(q, a) if q Î Q 2

Exercises • Draw a picture that graphically displays how the preceding proof works. • Draw an NFA that accepts the concatenation of {w | w begins with a 1 and ends with a 0} and {w | w contains at least three 1 s}

Closure Under Star • Let N 1 = (Q 1, S, d 1, q 1, F 1) • Construct N = (Q, S, d, q 0, F) • Q = {q 0} U Q 1 • F = {q 0} U F 1

Closure Under Star d(q, a) = d 1(q, a) if q Î Q 1 and !(q Î F 1) d 1(q, a) if q Î F 1 and a <> e d 1(q, a) U {q 1} if q Î F 1 and a = e {q 1} if q = q 0 and a = e {} if q = q 0 and a <> e

Exercises • Draw a picture that graphically displays how the preceding proof works. • Draw an NFA that accepts the star of {w | w begins with a 1 and ends with a 0}.