Theory of Computation Nondeterministic Finite Automaton NFA An

Theory of Computation

Nondeterministic Finite Automaton (NFA) An NFA is a collection of three things 1) Finite states with one initial and some final states 2) Finite set of input letters (Σ) from which input strings are formed 3) Finite set of transitions, showing where to move if a letter is input at certain state, there may be more than one transition for certain letters and there may not be any transition for certain letters. 2

Observations The string is supposed to be accepted, if there exists at least one successful path, otherwise rejected. NFA can be considered to be an intermediate structure between FA and TG. 3

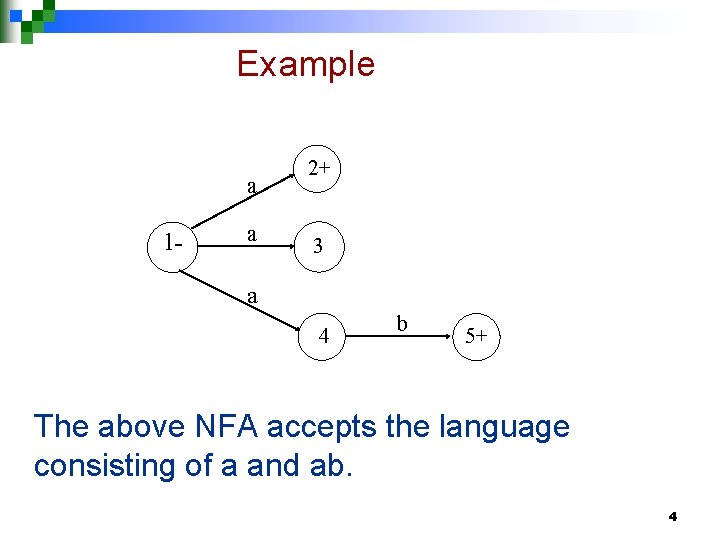
Example a 1 - a 2+ 3 a 4 b 5+ The above NFA accepts the language consisting of a and ab. 4

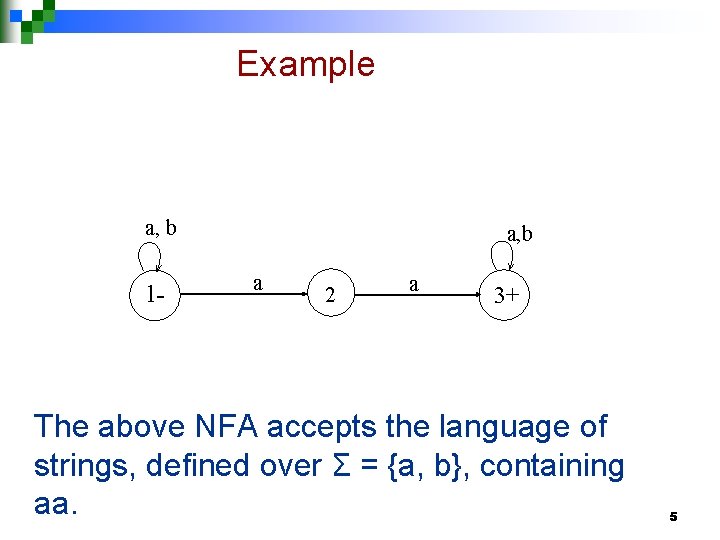
Example a, b 1 - a, b a 2 a 3+ The above NFA accepts the language of strings, defined over Σ = {a, b}, containing aa. 5

Non-determinism This refers to situations in which the next state of a computation is not uniquely determined by the current state. n In these situations we know only a range of possibilities n 6

Converting an FA to an equivalent NFA n If a language is accepted by an FA, then there exists a TG accepting that language(Kleene’s theorem). n Since, an NFA is also a TG, there exists an NFA accepting the language accepted by the given FA. In this case these FA and NFA are said to be equivalent to each others. 7

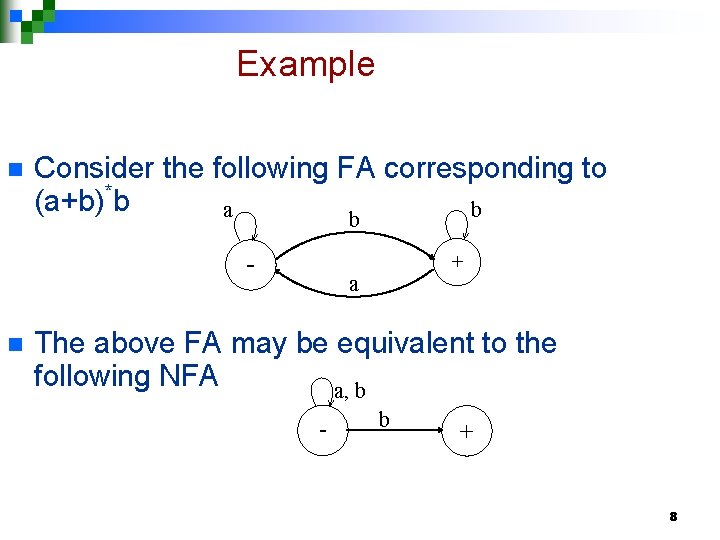
Example n Consider the following FA corresponding to (a+b)*b a b b n + a The above FA may be equivalent to the following NFA a, b - b + 8

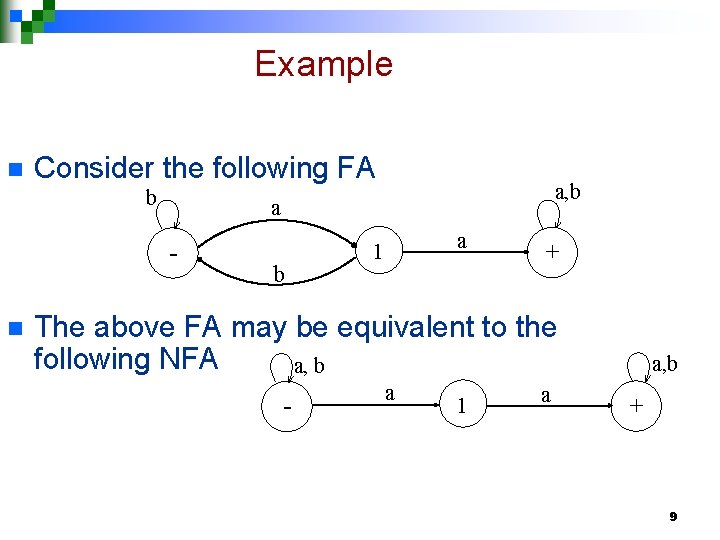
Example n Consider the following FA b a n a, b b a 1 + The above FA may be equivalent to the following NFA a, b - a 1 a a, b + 9

Note n n Every FA can be considered to be an NFA, but the converse may not true. Every NFA can be considered to be a TG, but the converse may not true. 10

NFA to FA An NFA can be considered to be a TG, so a RE corresponding to the given NFA can be determined Again using Kleene’s theorem, an FA can be built corresponding to that RE. 11

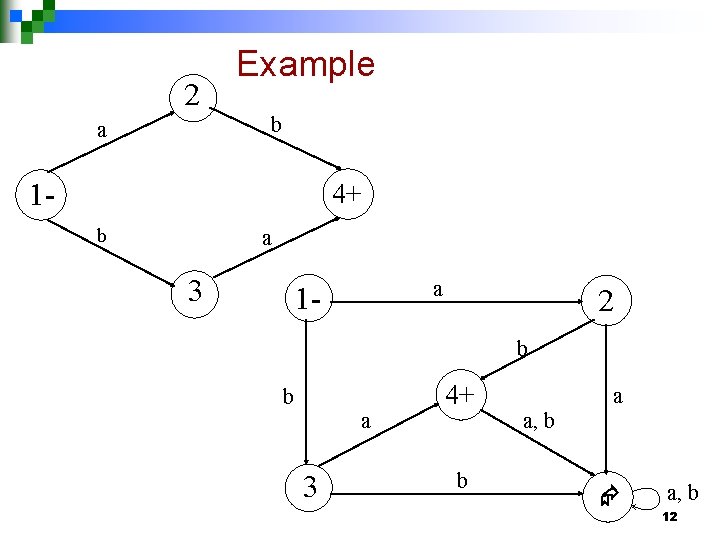
2 Example b a 1 - 4+ b a 3 a 1 - 2 b b a 3 4+ b a a, b 12

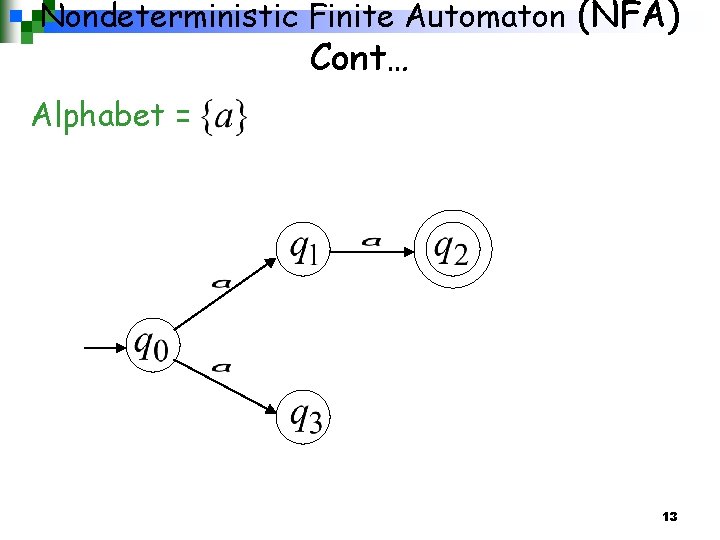
Nondeterministic Finite Automaton (NFA) Cont… Alphabet = 13

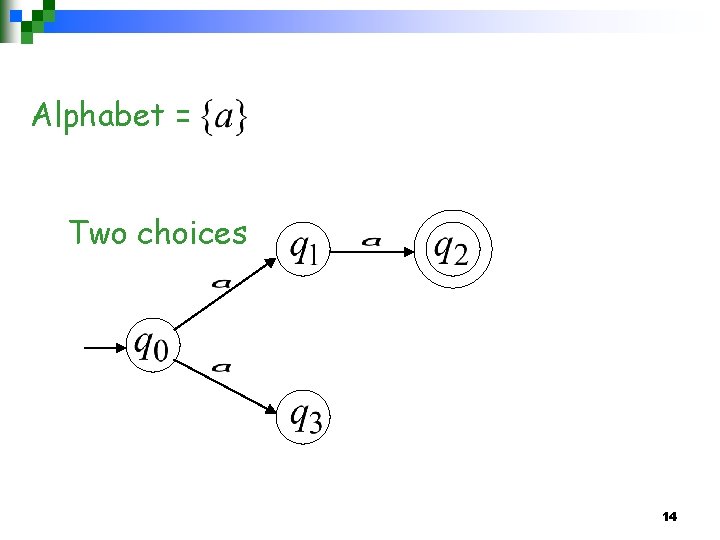
Alphabet = Two choices 14

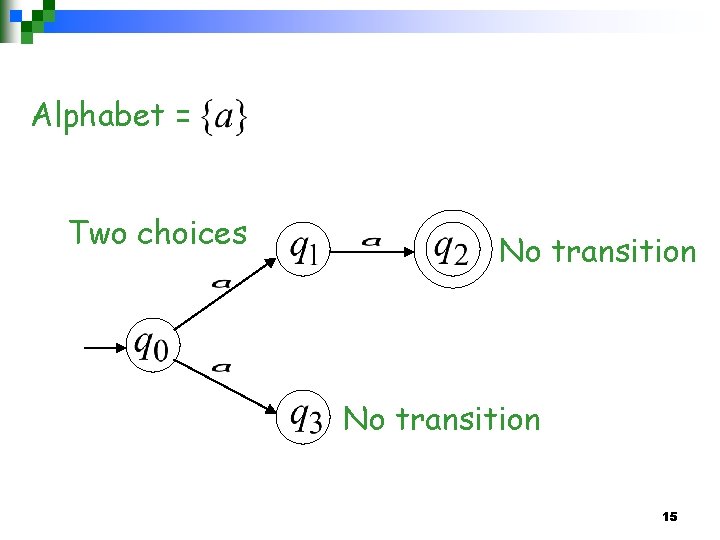
Alphabet = Two choices No transition 15

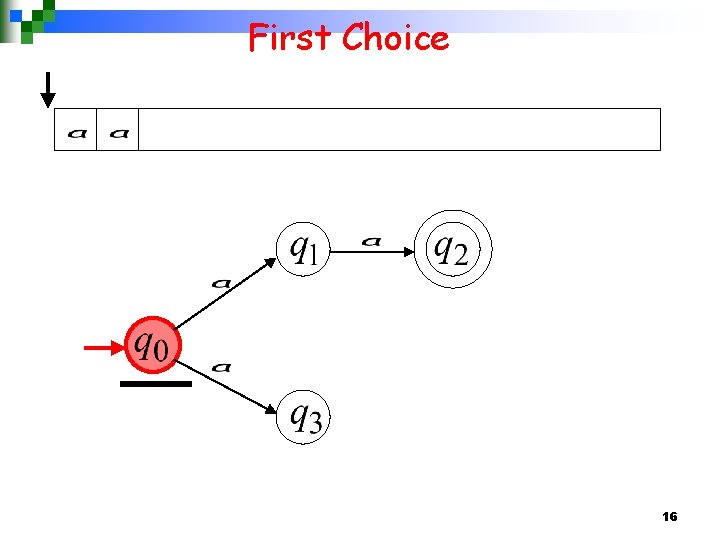
First Choice 16

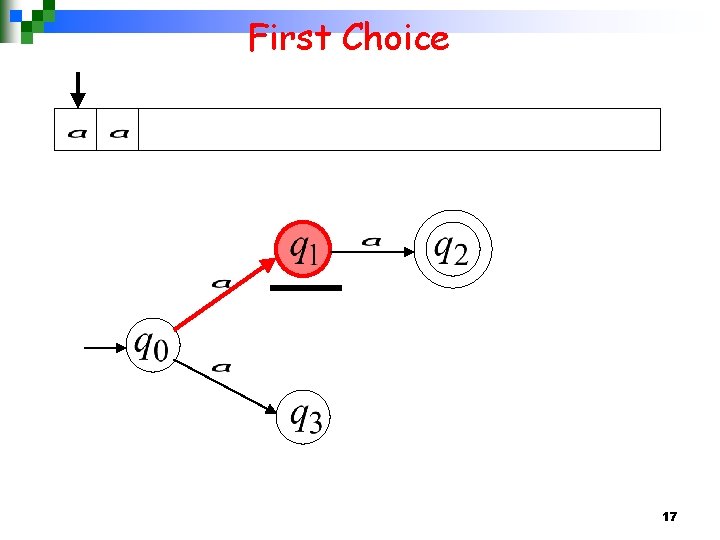
First Choice 17

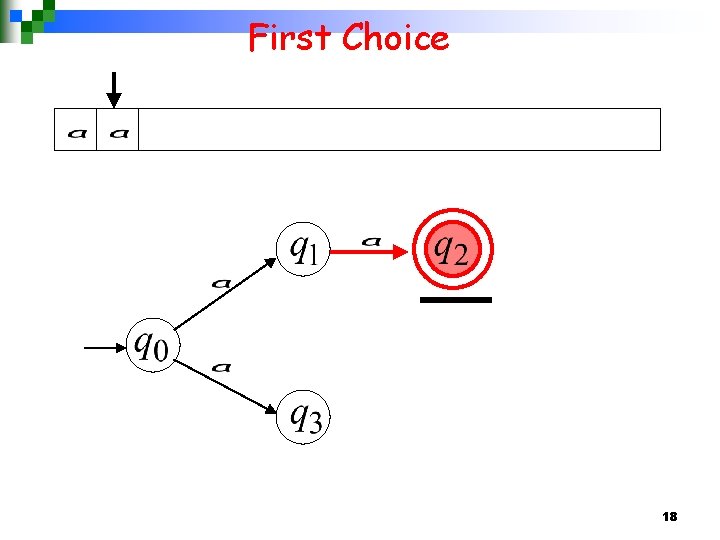
First Choice 18

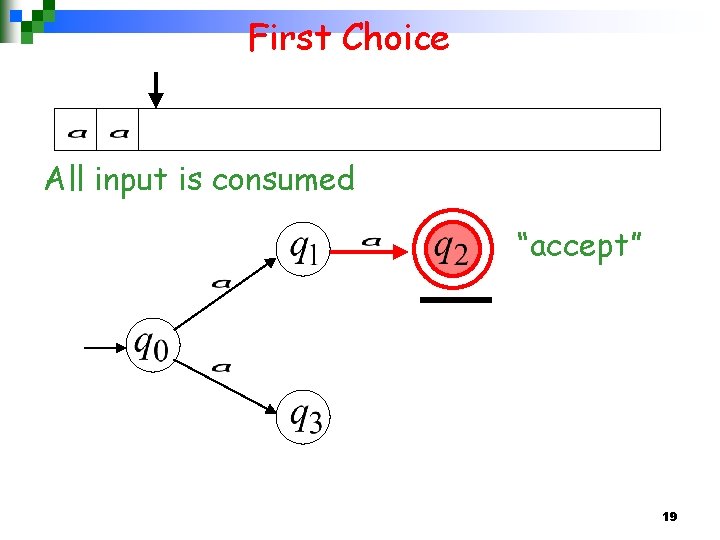
First Choice All input is consumed “accept” 19

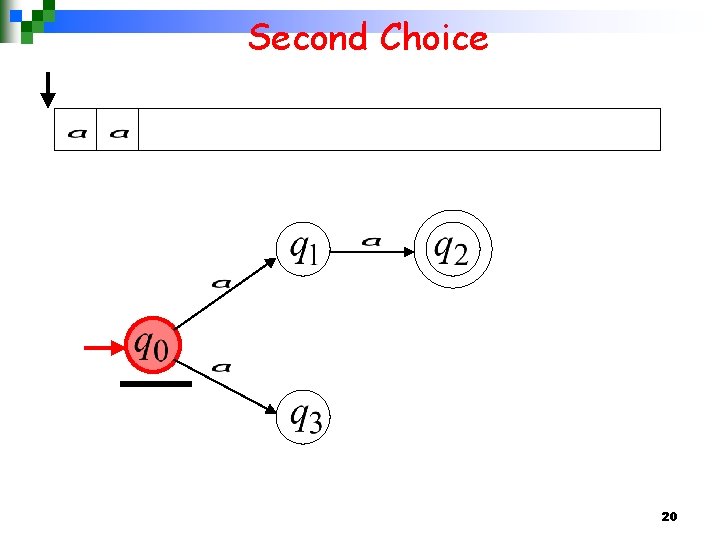
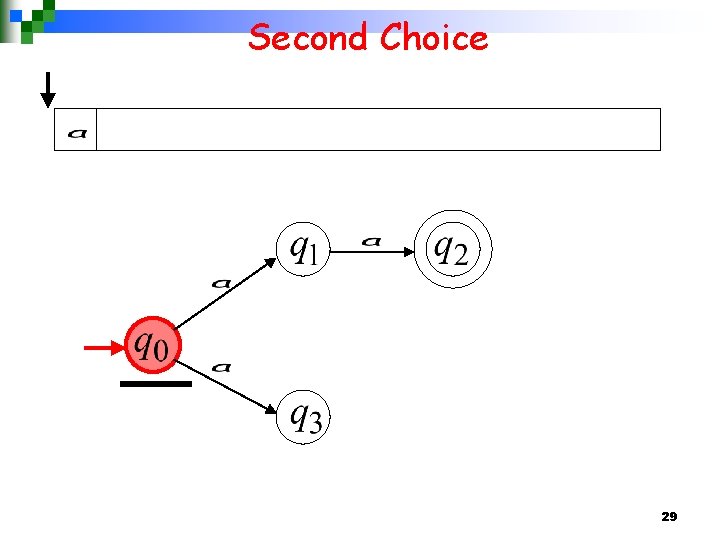
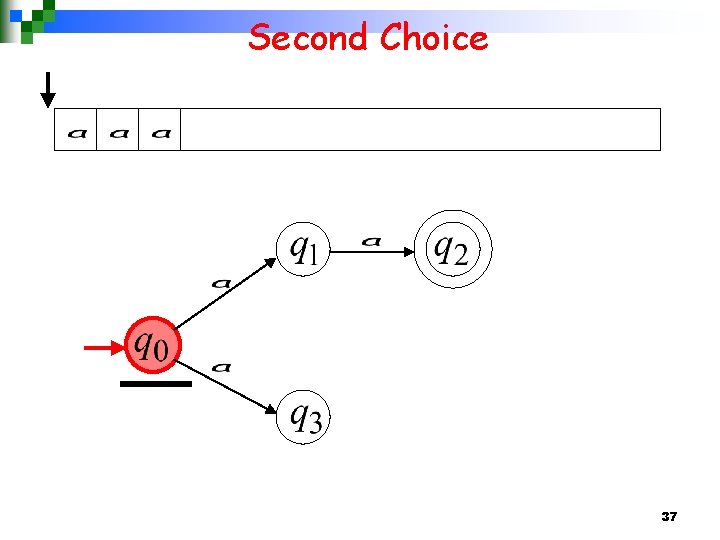
Second Choice 20

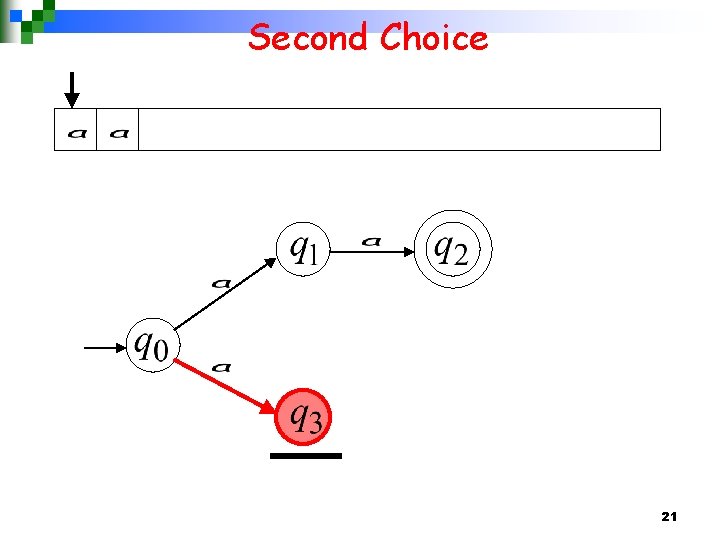
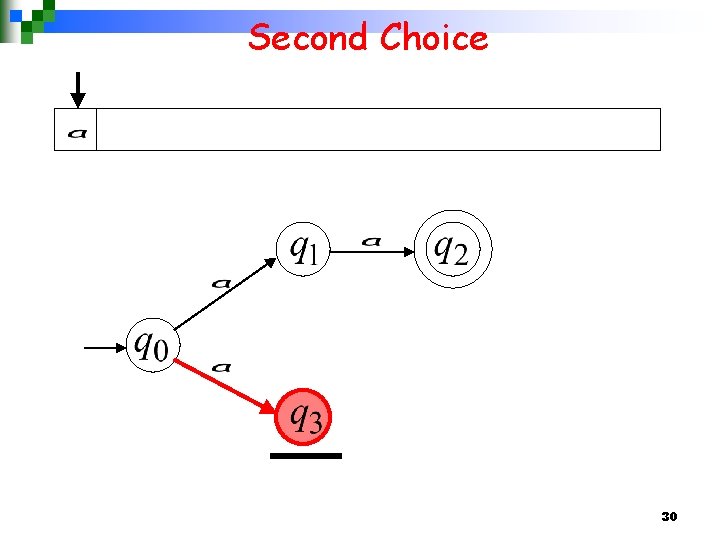
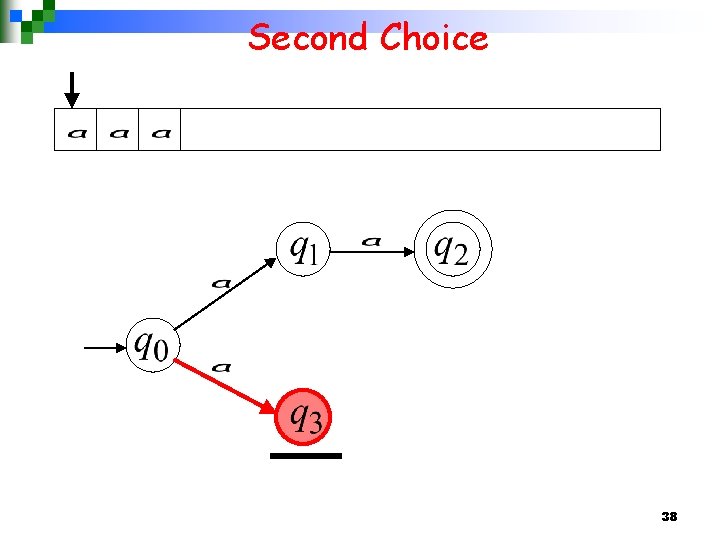
Second Choice 21

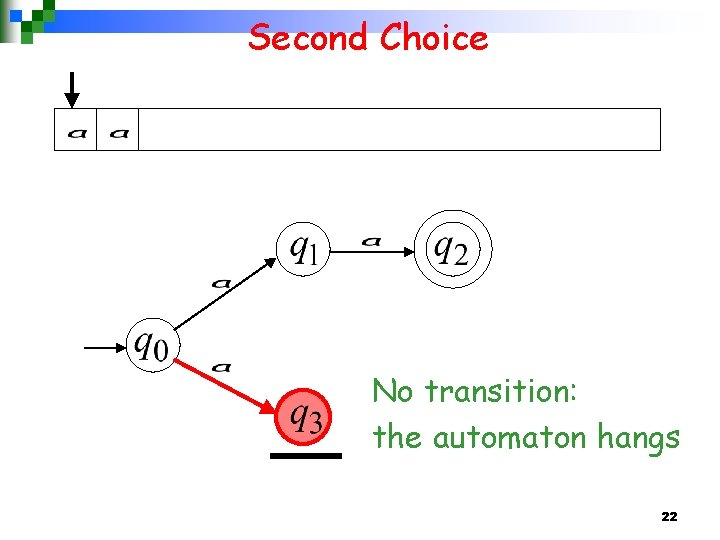
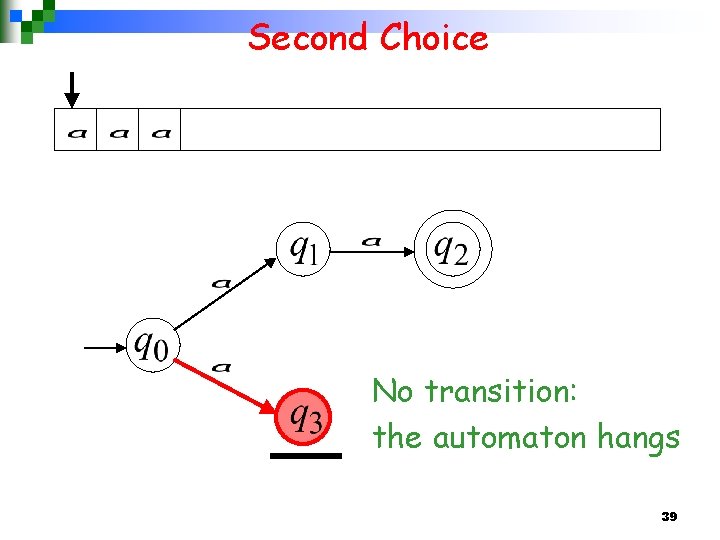
Second Choice No transition: the automaton hangs 22

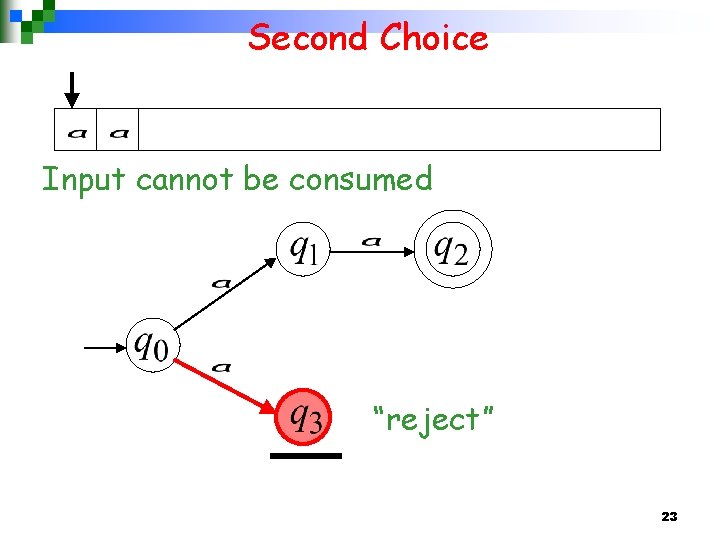
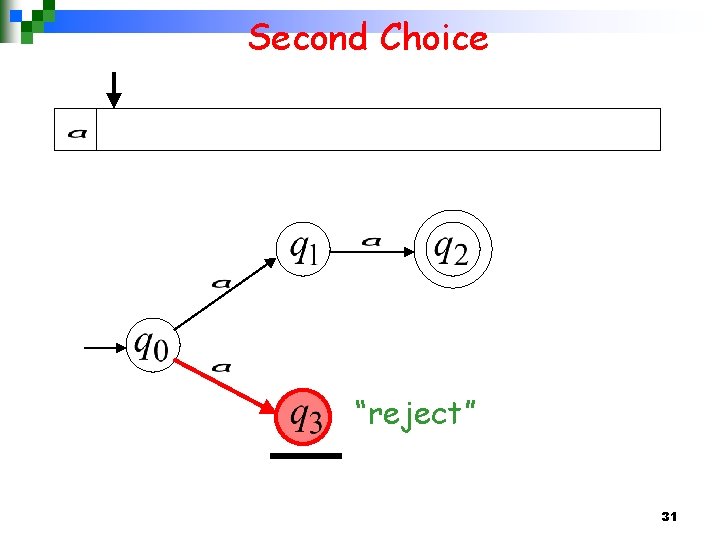
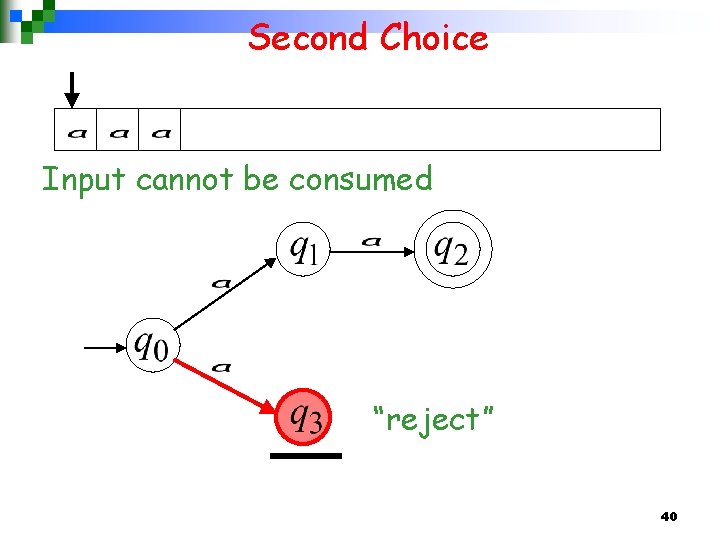
Second Choice Input cannot be consumed “reject” 23

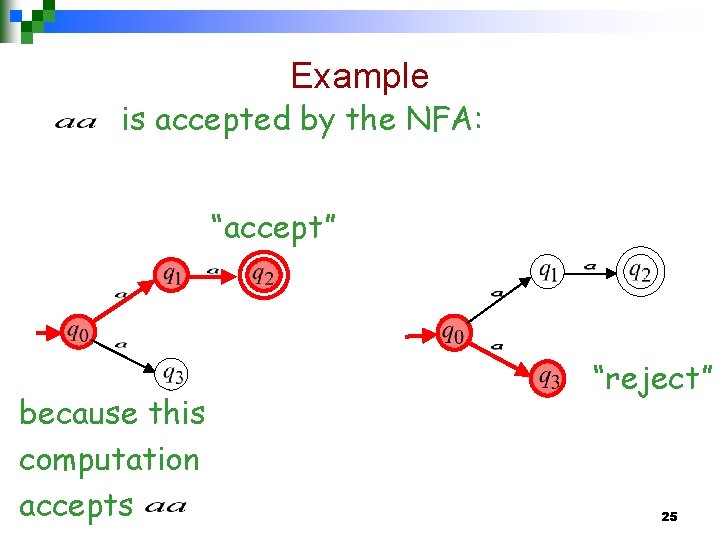
An NFA accepts a string: if there is a computation of the NFA that accepts the string i. e. , all the input is consumed and the automaton is in an accepting state 24

Example is accepted by the NFA: “accept” because this computation accepts “reject” 25

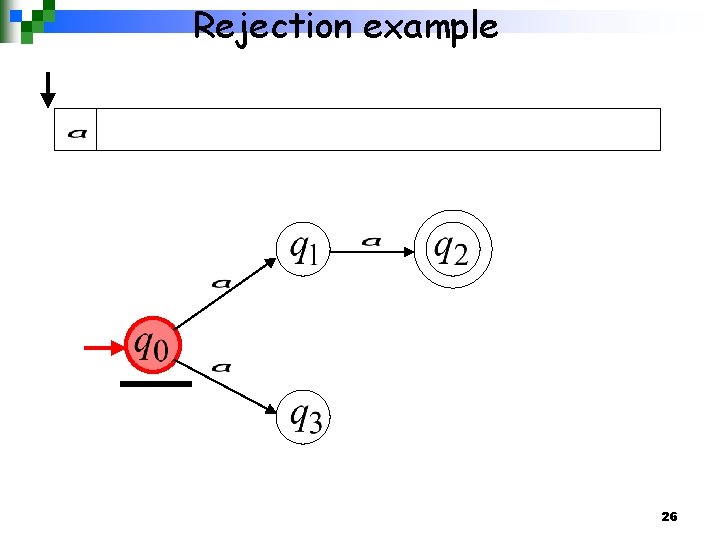
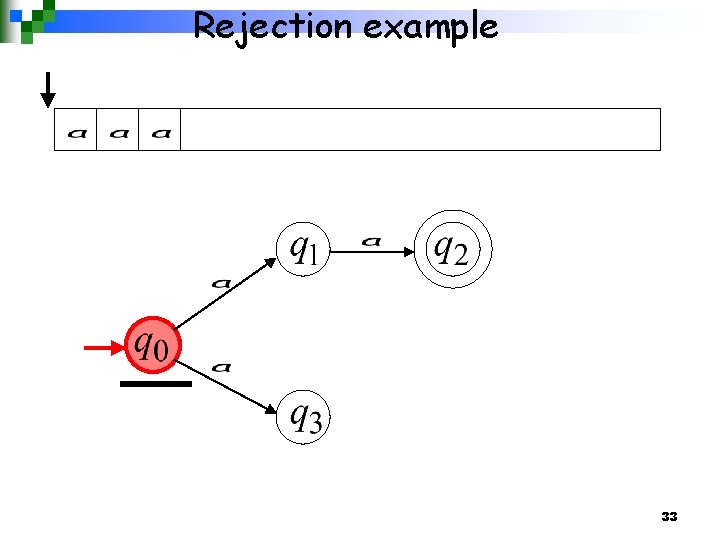
Rejection example 26

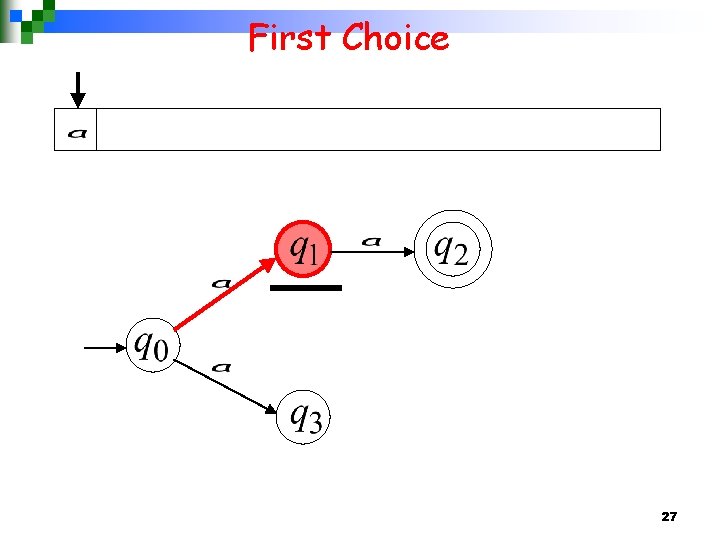
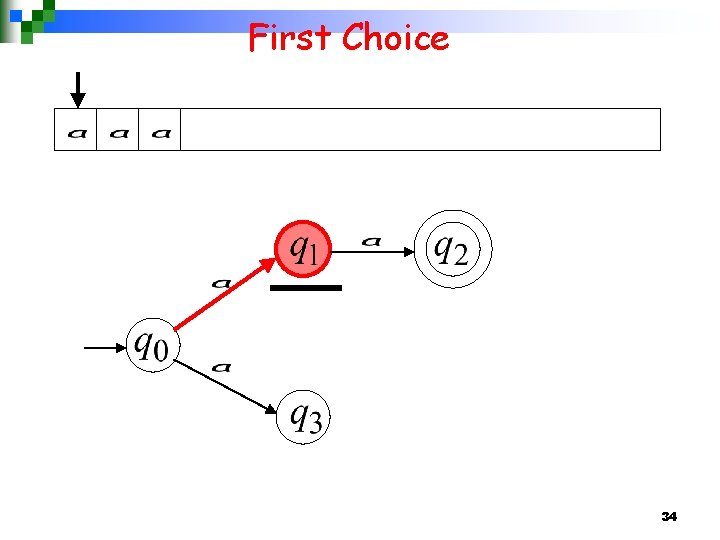
First Choice 27

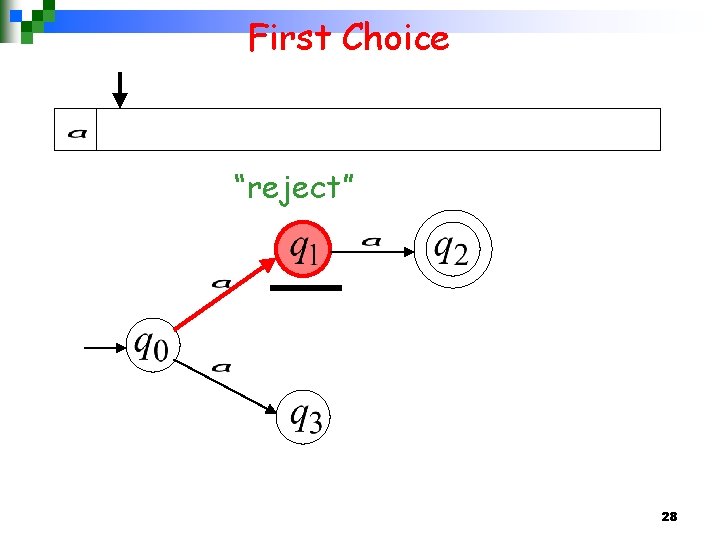
First Choice “reject” 28

Second Choice 29

Second Choice 30

Second Choice “reject” 31

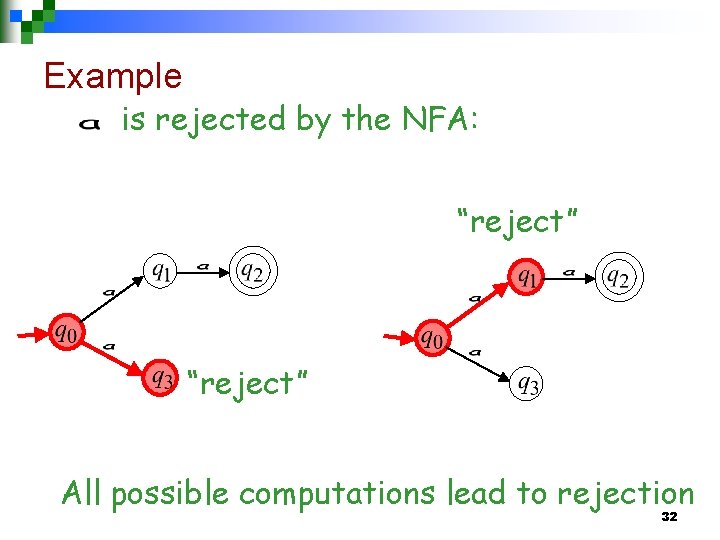
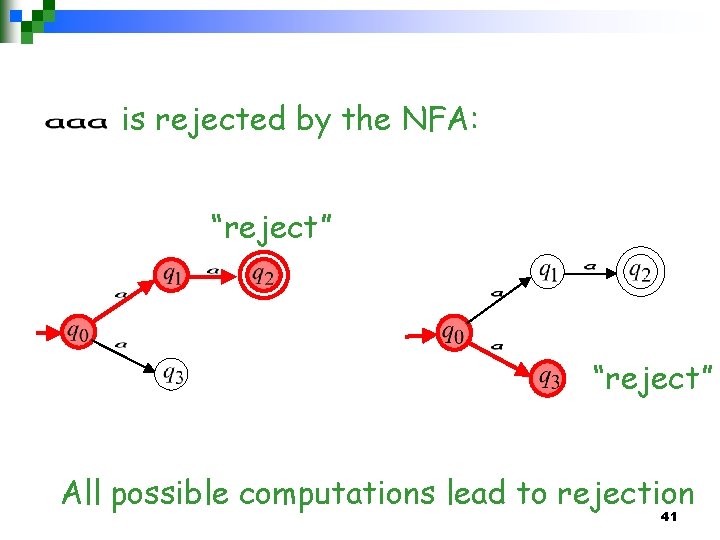
Example is rejected by the NFA: “reject” All possible computations lead to rejection 32

Rejection example 33

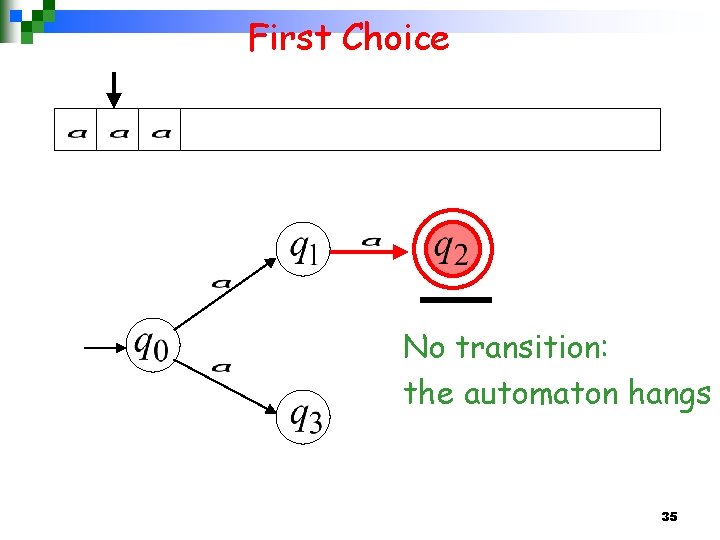
First Choice 34

First Choice No transition: the automaton hangs 35

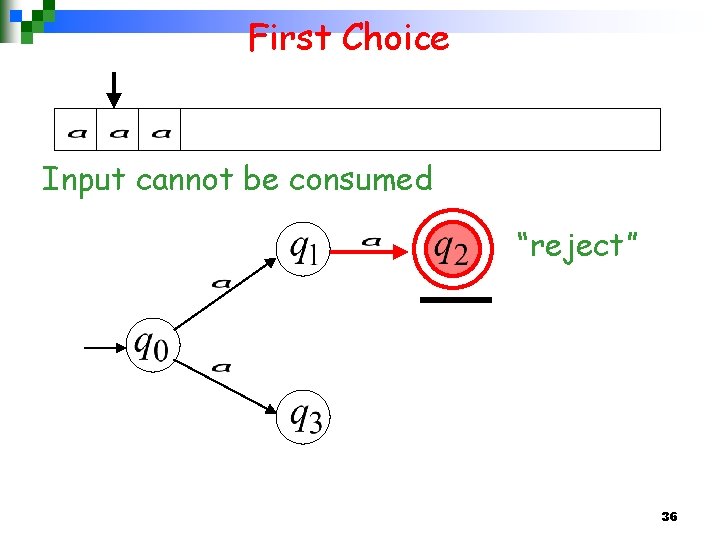
First Choice Input cannot be consumed “reject” 36

Second Choice 37

Second Choice 38

Second Choice No transition: the automaton hangs 39

Second Choice Input cannot be consumed “reject” 40

is rejected by the NFA: “reject” All possible computations lead to rejection 41

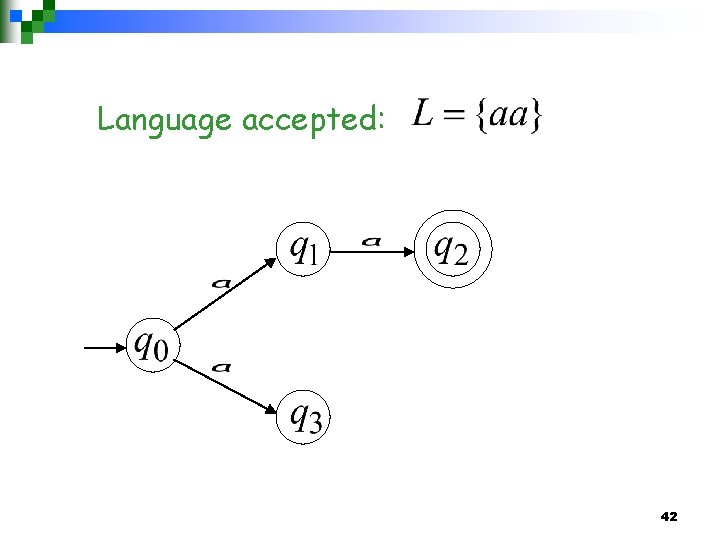
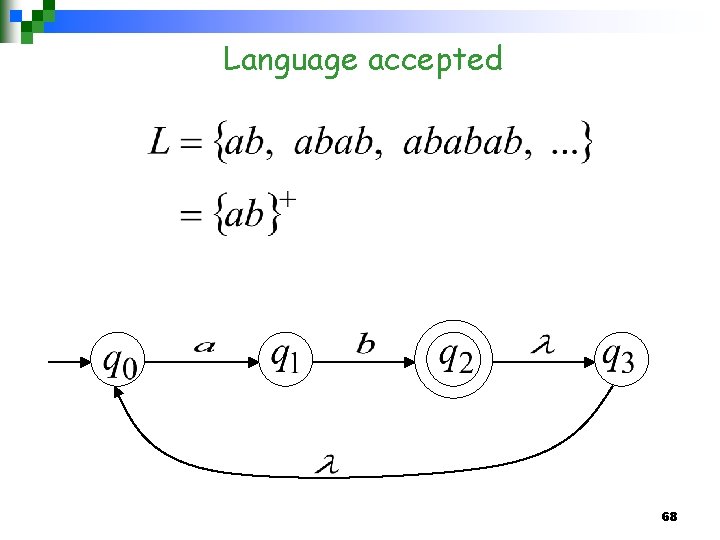
Language accepted: 42

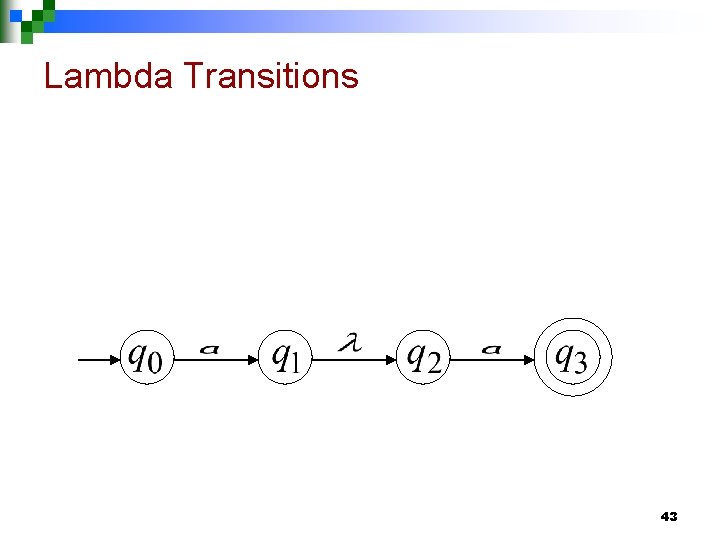
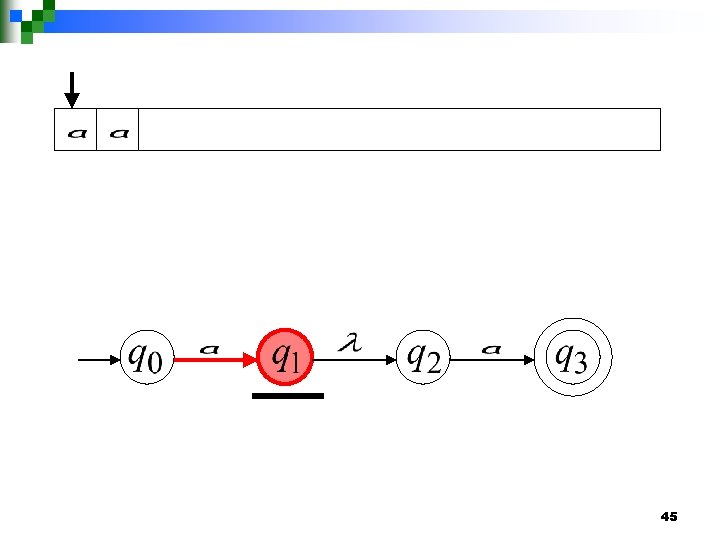
Lambda Transitions 43

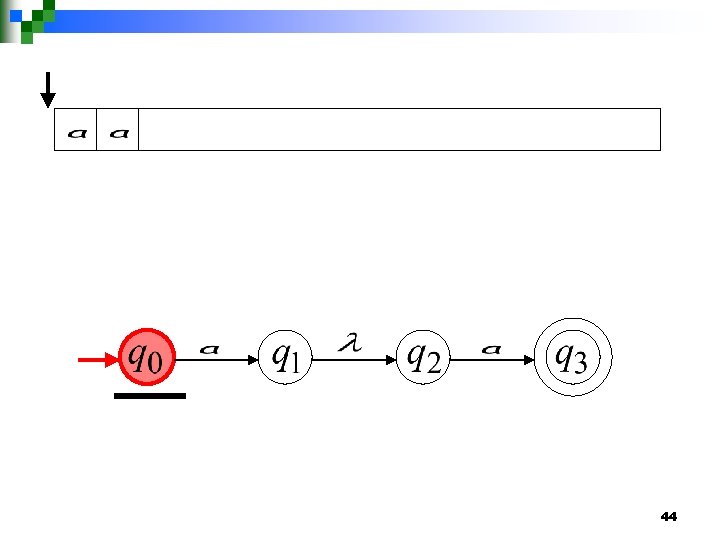
44

45

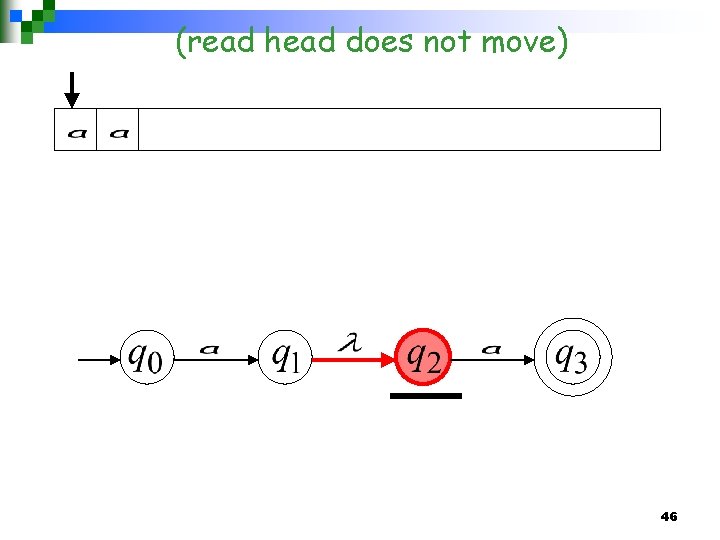
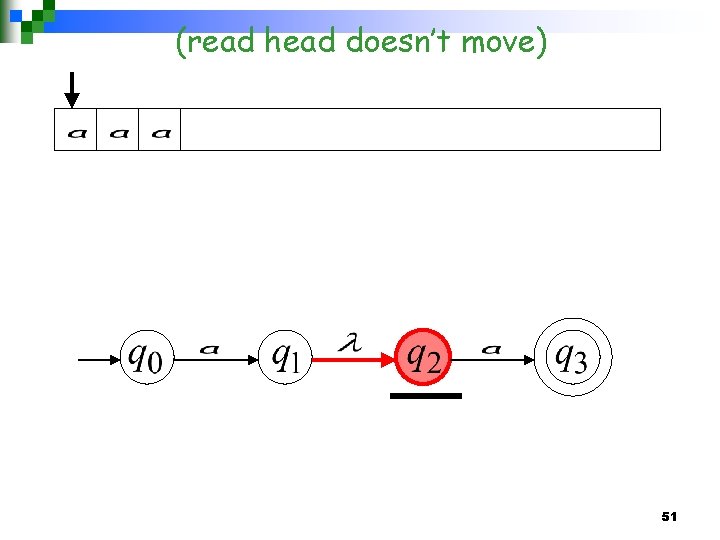
(read head does not move) 46

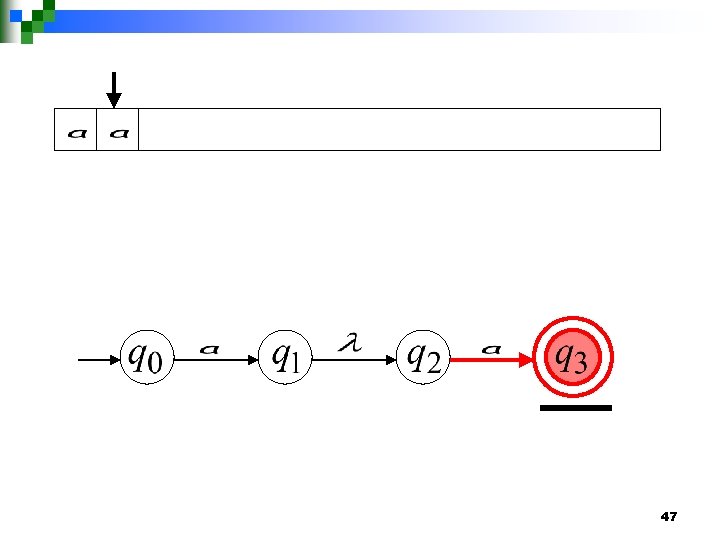
47

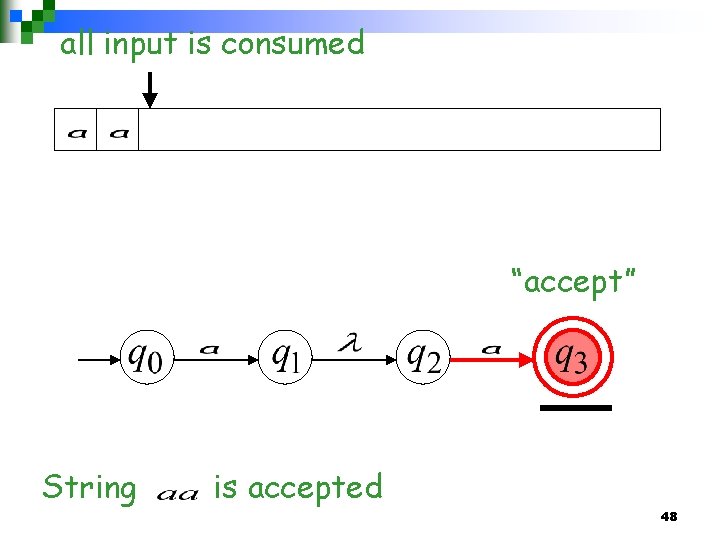
all input is consumed “accept” String is accepted 48

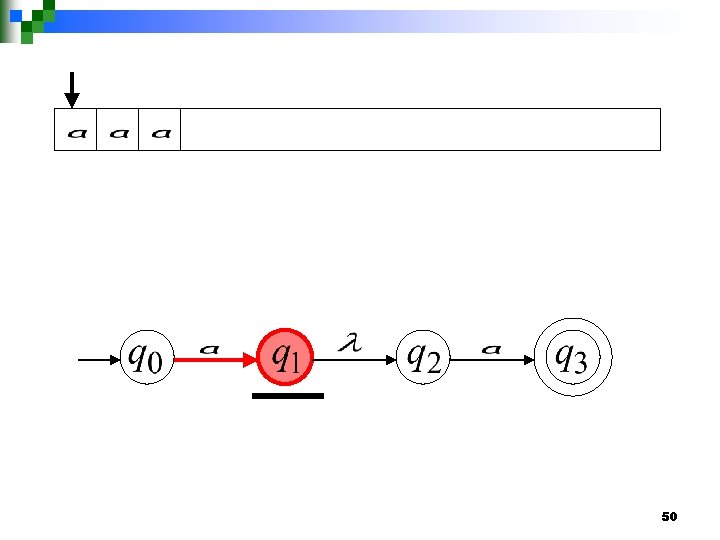
Rejection Example 49

50

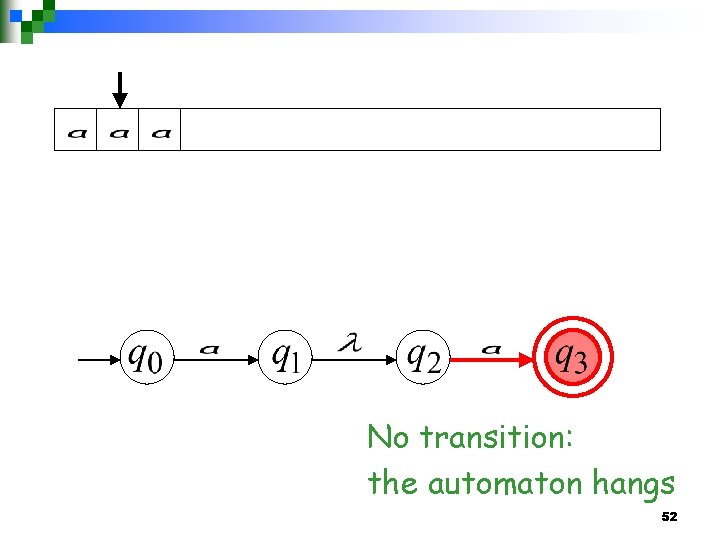
(read head doesn’t move) 51

No transition: the automaton hangs 52

Input cannot be consumed “reject” String is rejected 53

Language accepted: 54

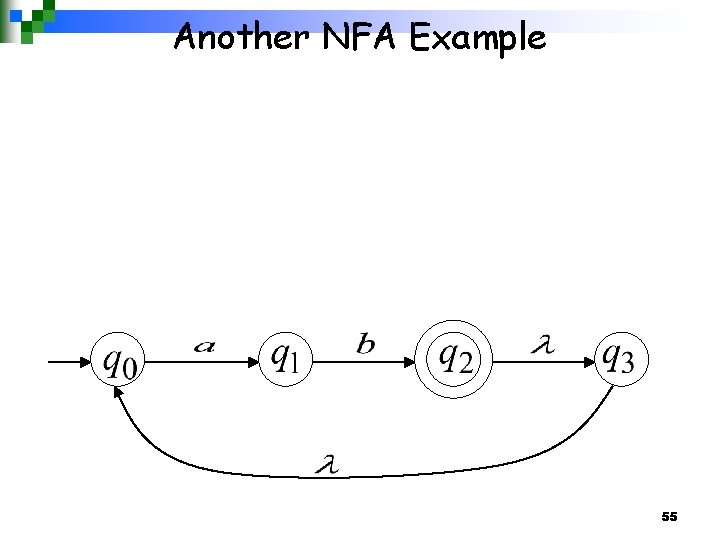
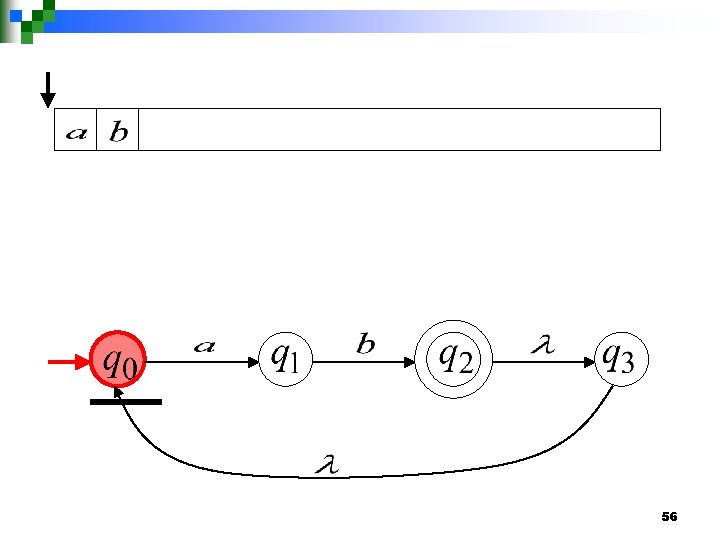
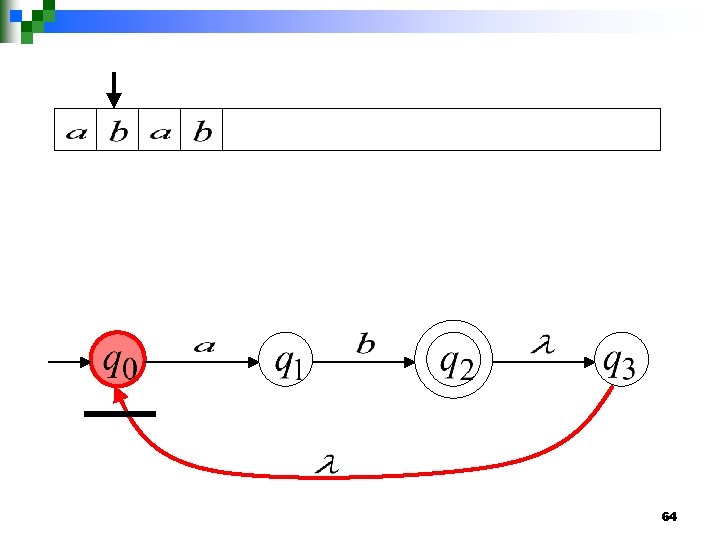
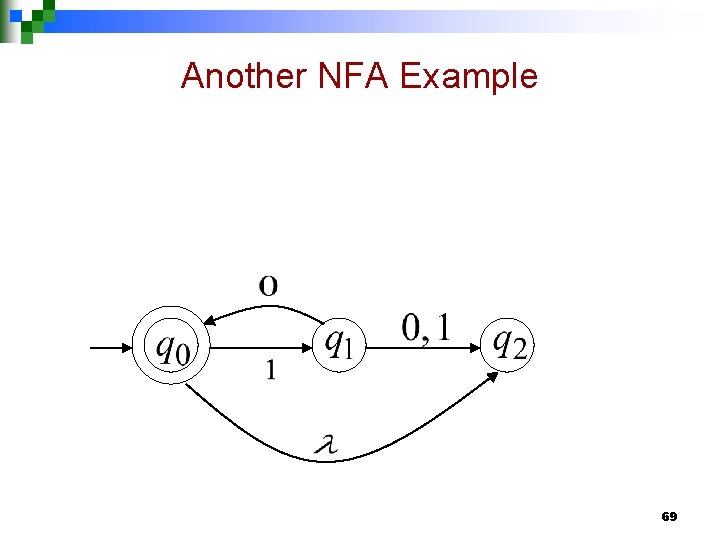
Another NFA Example 55

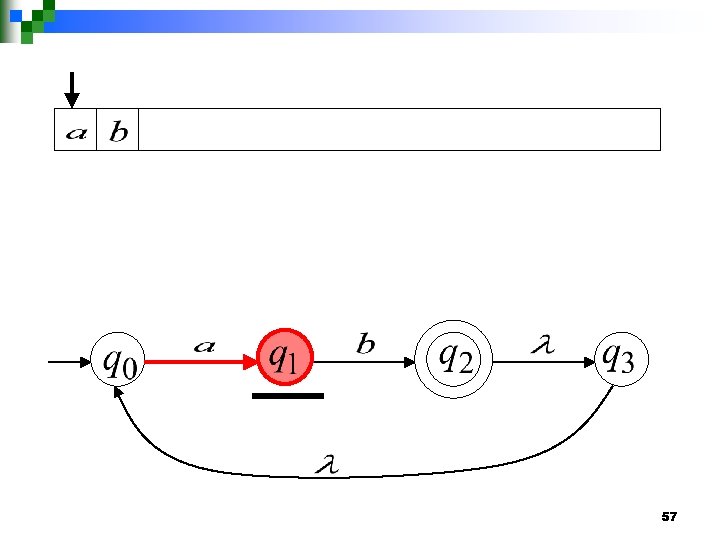
56

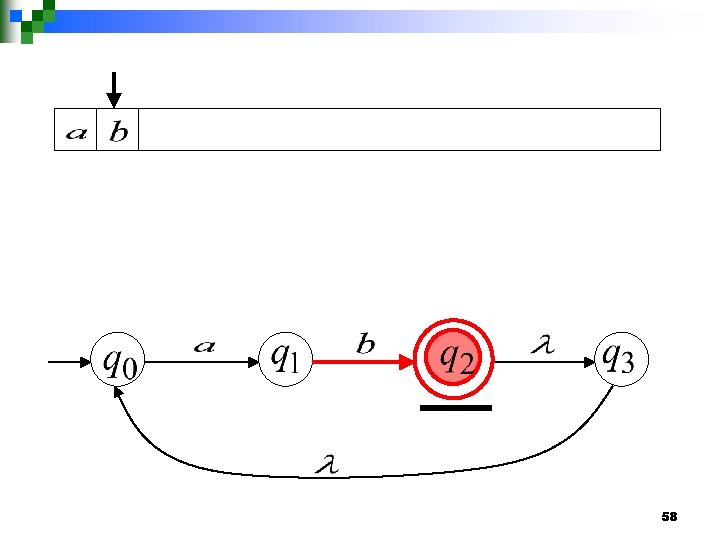
57

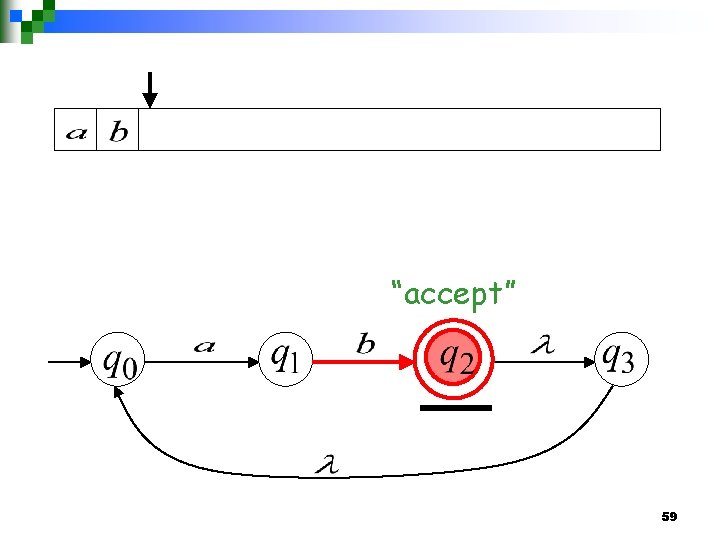
58

“accept” 59

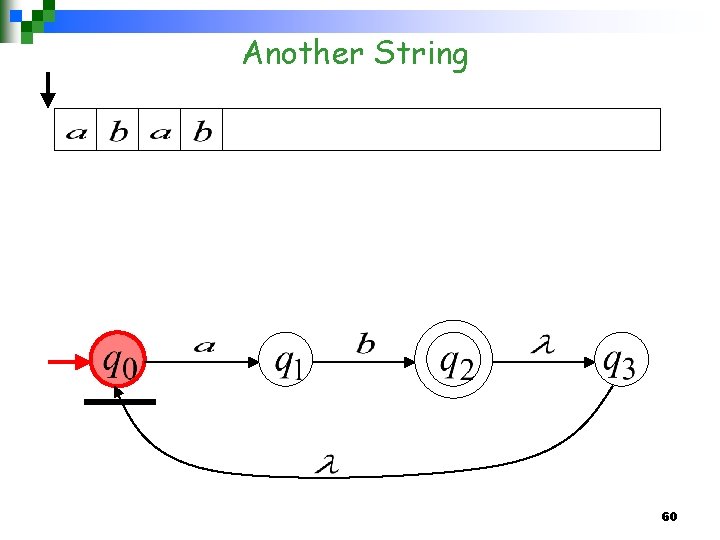
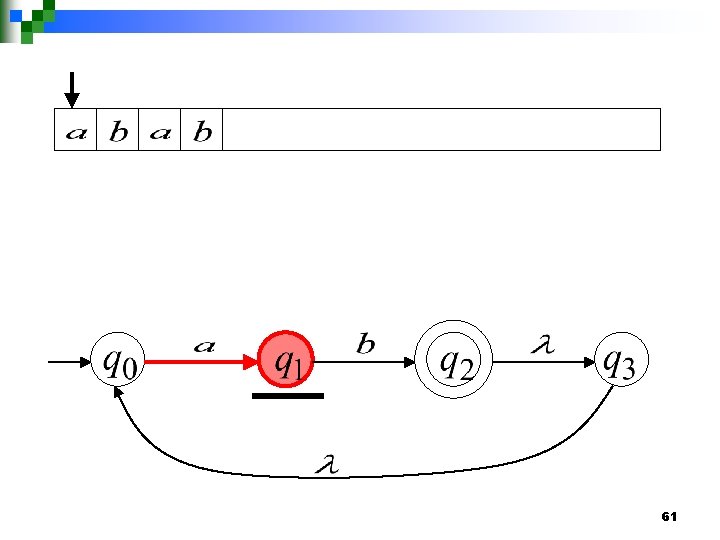
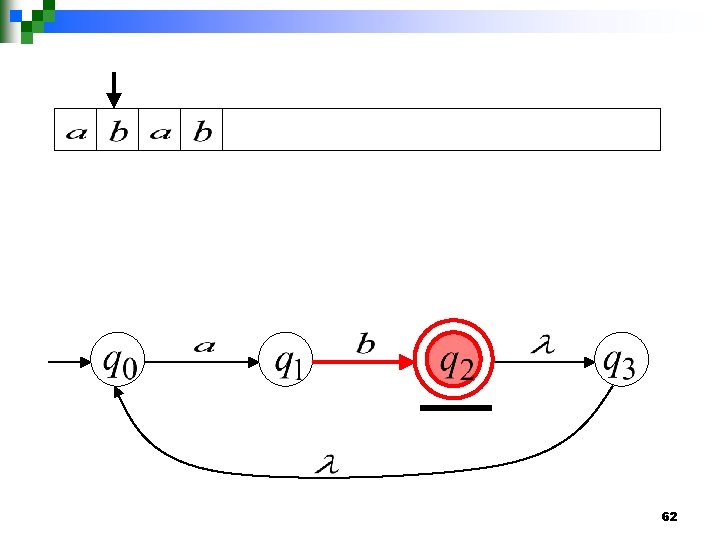
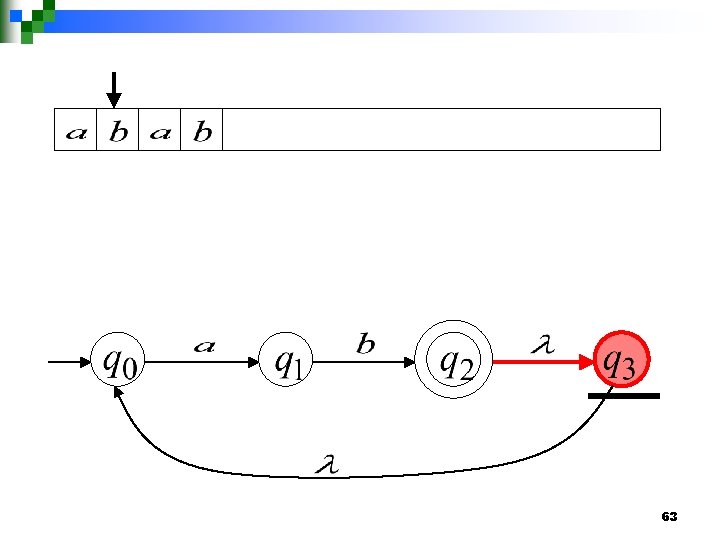
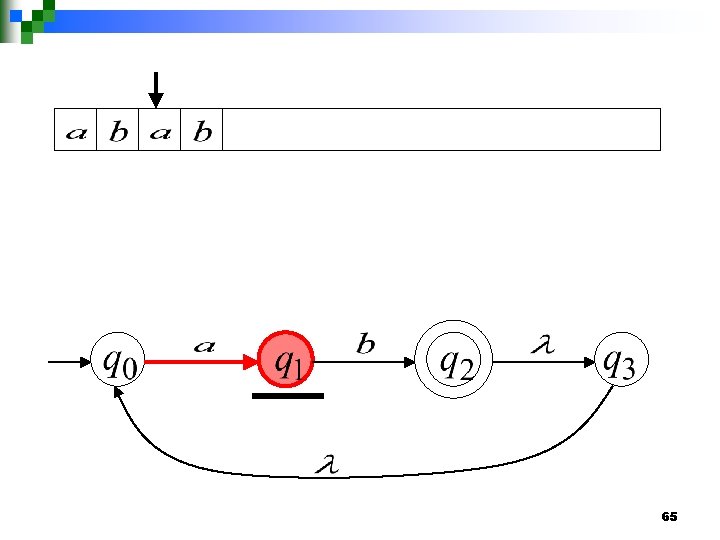
Another String 60

61

62

63

64

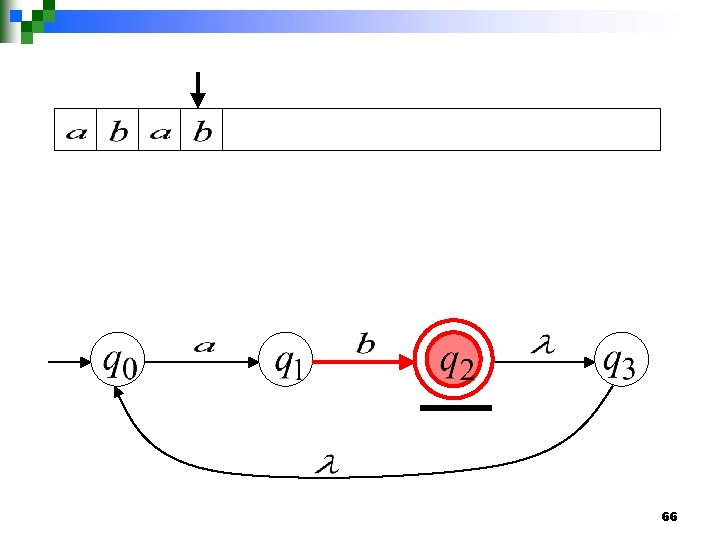
65

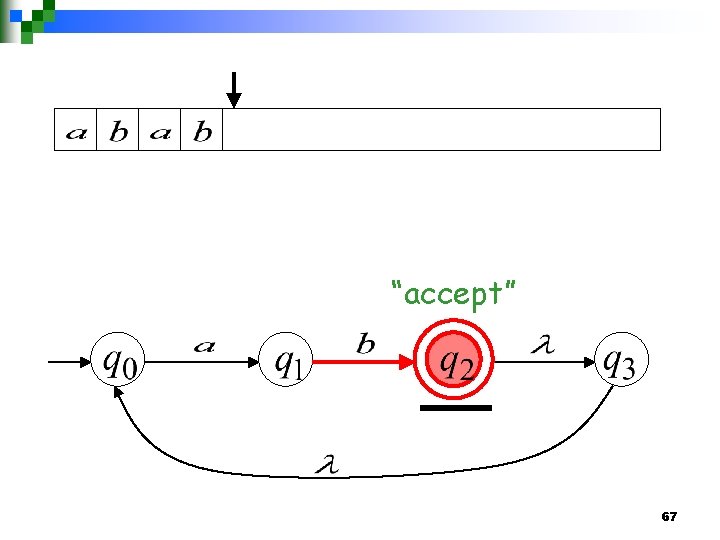
66

“accept” 67

Language accepted 68

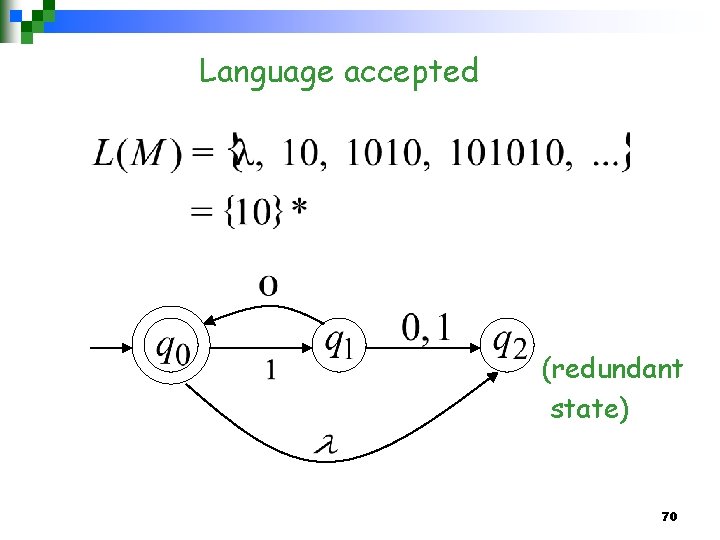
Another NFA Example 69

Language accepted (redundant state) 70

Remarks: • The symbol never appears on the input state • Simple automata: 71

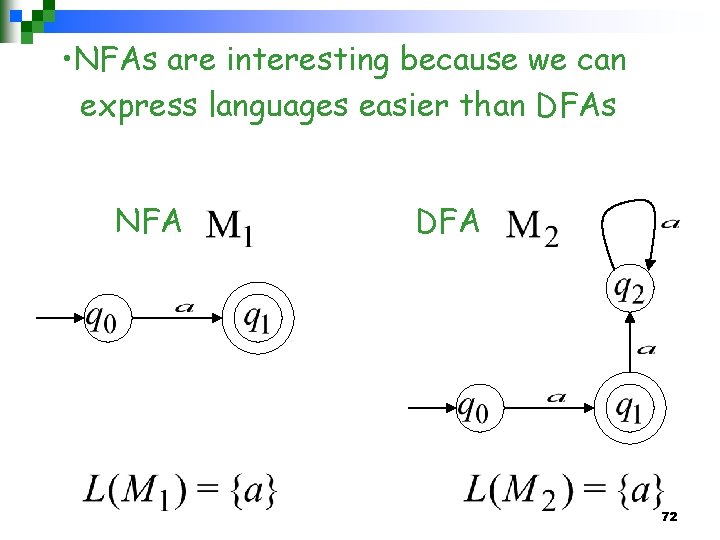
• NFAs are interesting because we can express languages easier than DFAs NFA DFA 72

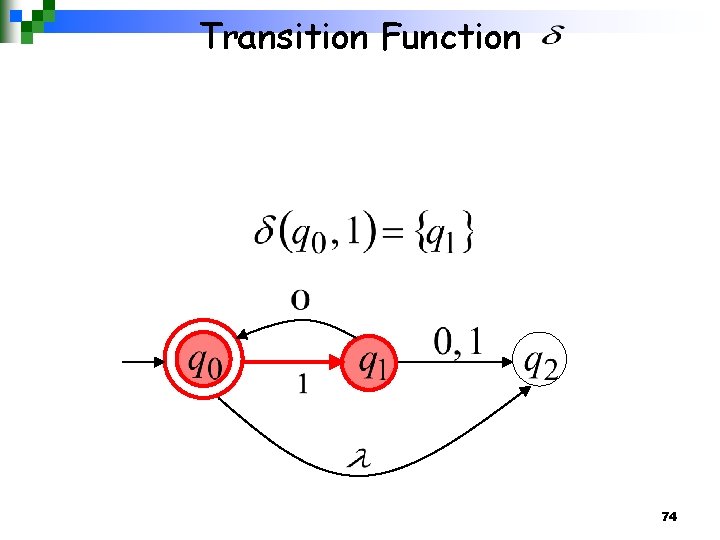
Formal Definition of NFAs n Set of states, i. e. Input aplhabet, i. e. Transition function Initial state Accepting states 73

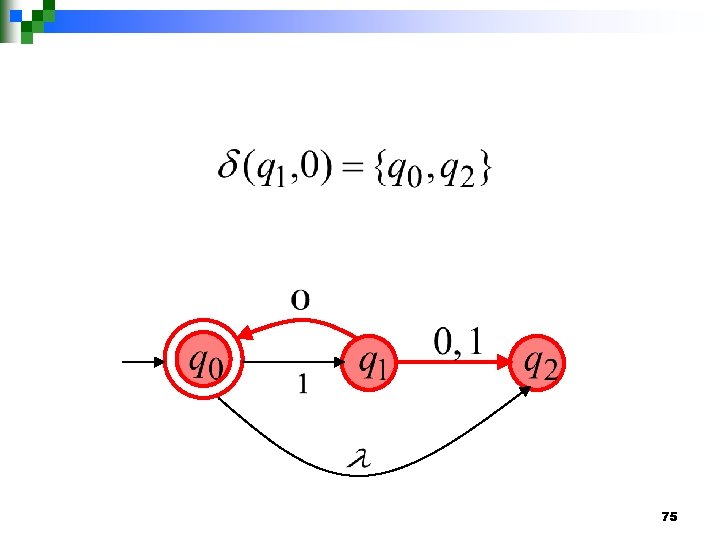
Transition Function 74

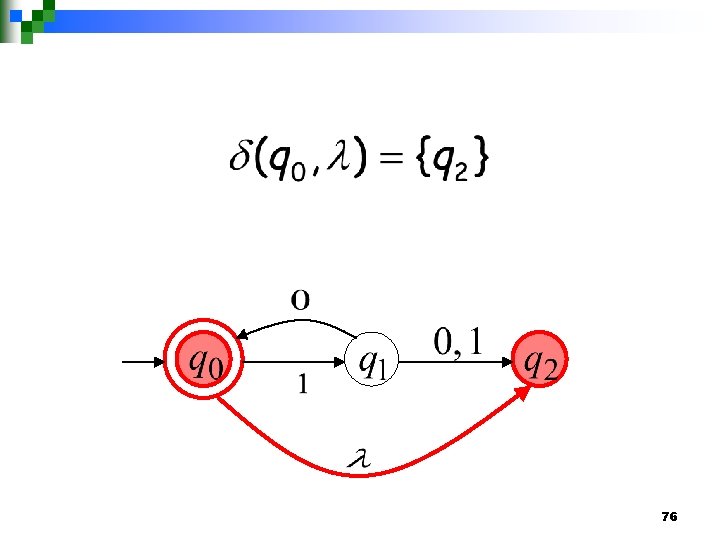
75

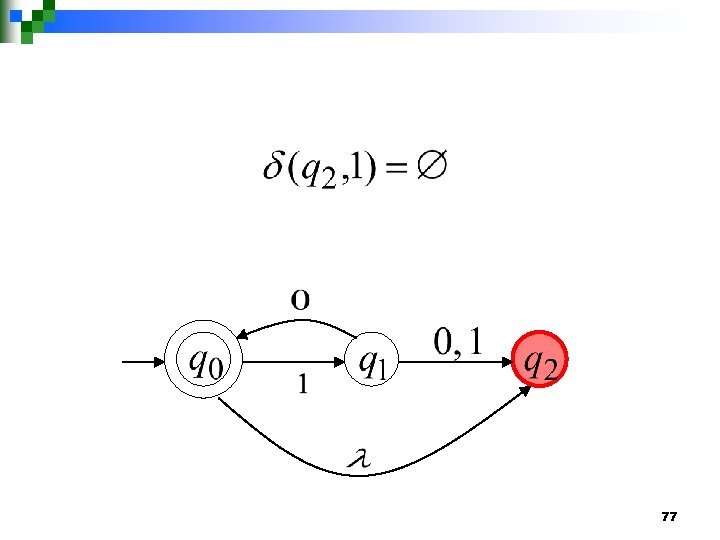
76

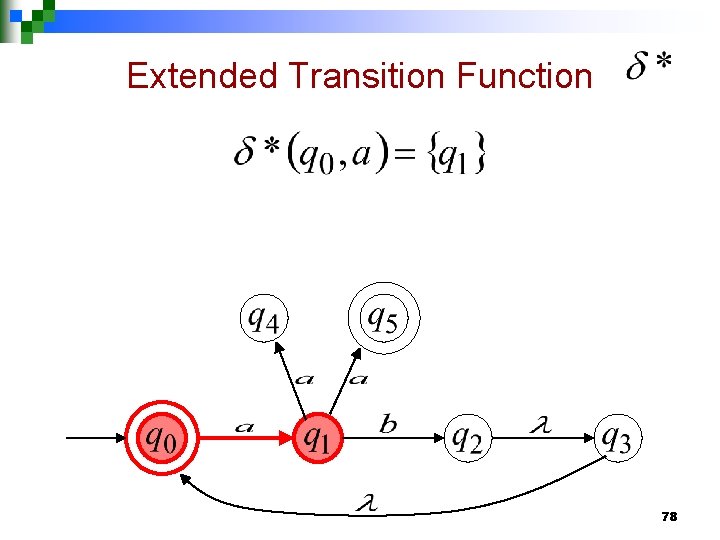
77

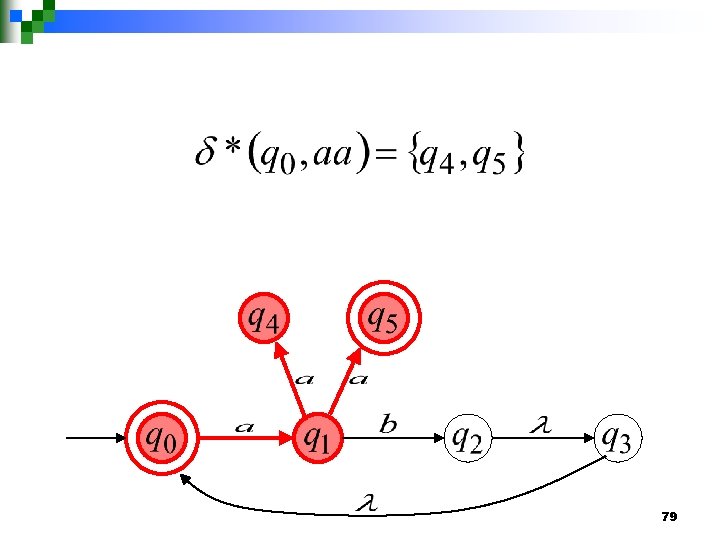
Extended Transition Function 78

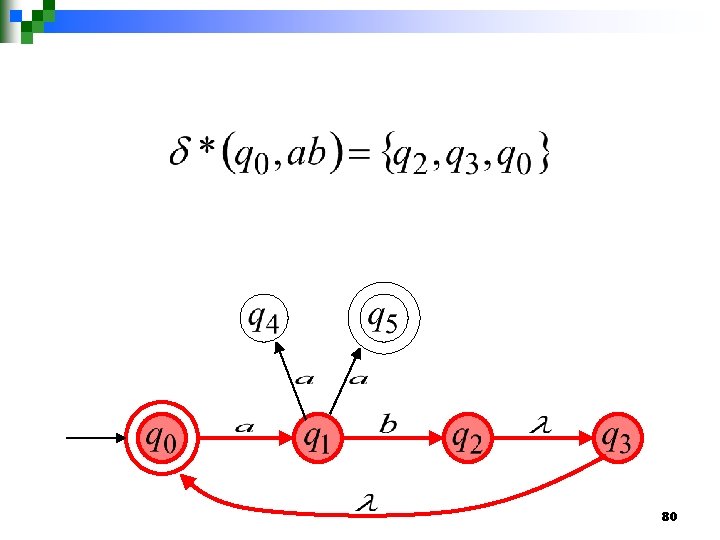
79

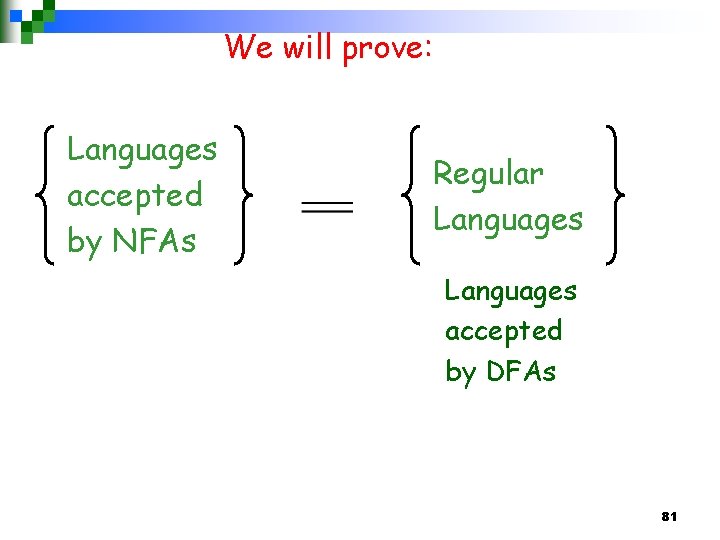
80

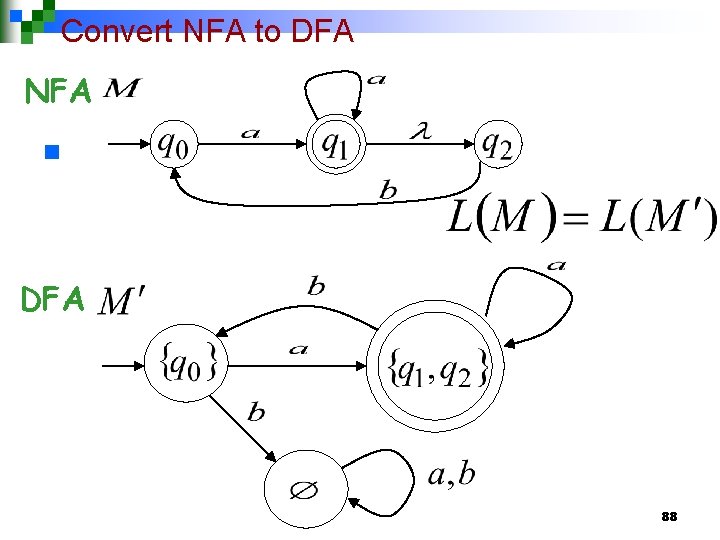
We will prove: Languages accepted by NFAs Regular Languages accepted by DFAs 81

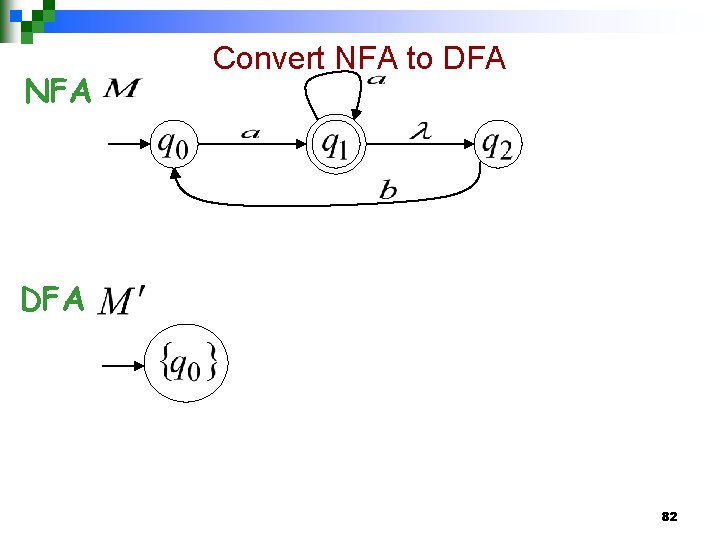
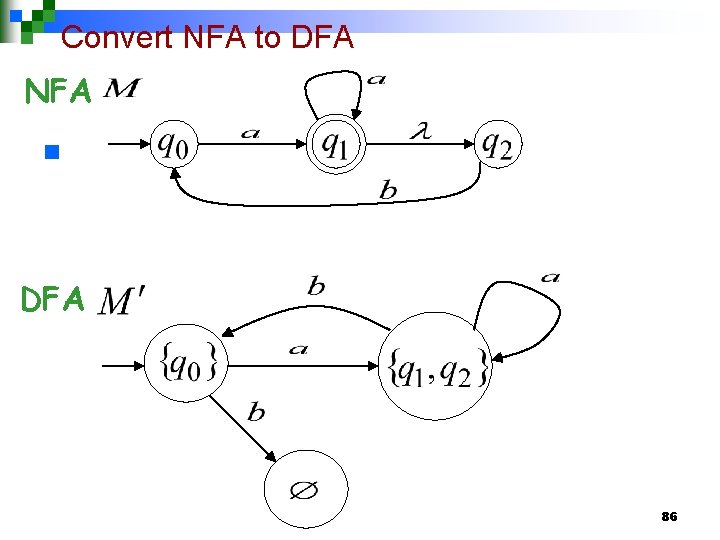
NFA Convert NFA to DFA 82

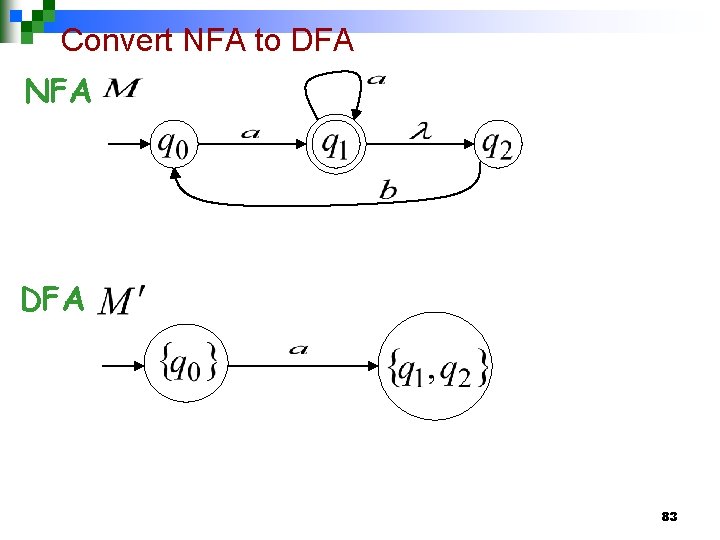
Convert NFA to DFA NFA DFA 83

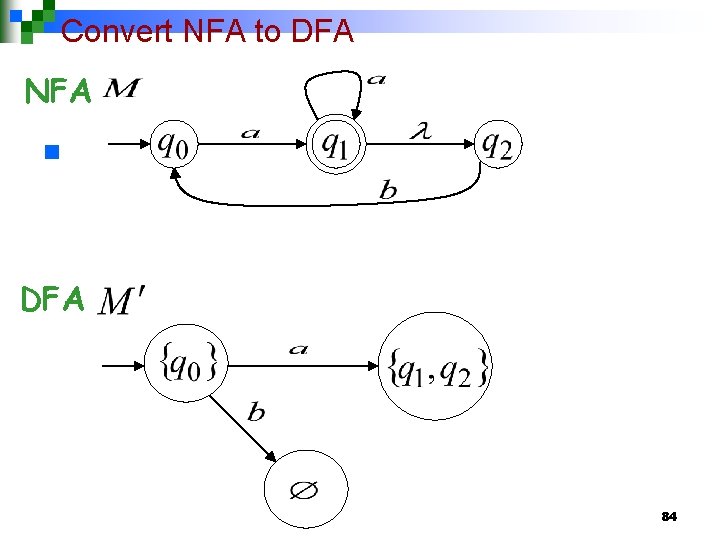
Convert NFA to DFA NFA n DFA 84

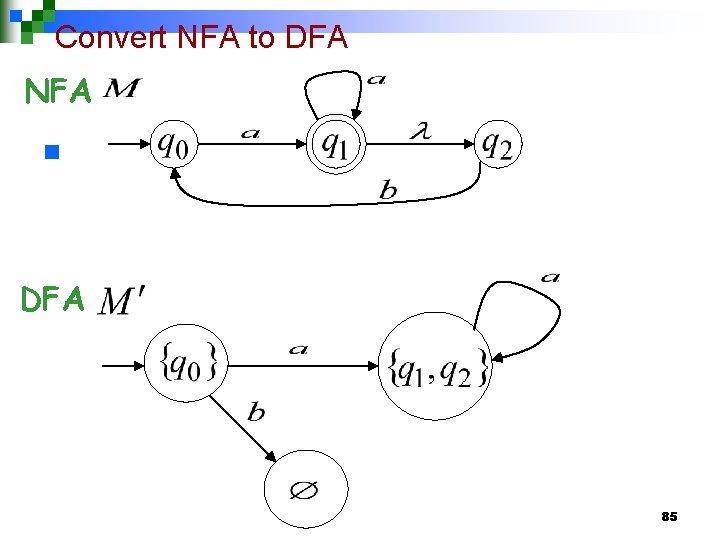
Convert NFA to DFA NFA n DFA 85

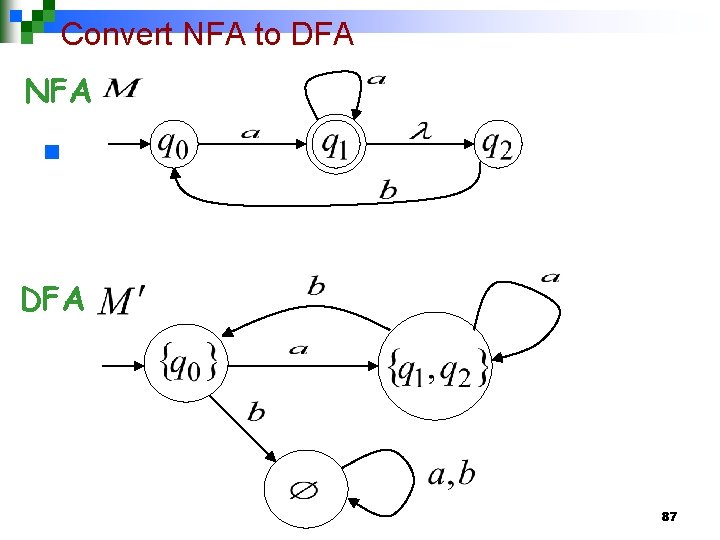
Convert NFA to DFA NFA n DFA 86

Convert NFA to DFA NFA n DFA 87

Convert NFA to DFA NFA n DFA 88

Thank You! 89