TEORIA DAS FILAS Introduo Por que aparecem as

TEORIA DAS FILAS

Introdução � Por que aparecem as filas? � Não é eficiente, nem racional, que cada um disponha de todos os recursos individualmente. Por exemplo: �que cada pessoa disponha do uso exclusivo de uma rua para se movimentar �que cada pessoa tenha um supermercado para o seu abastecimento exclusivo � Recursos limitados devem ser compartilhados.

Introdução � Ao compartilhar recursos, pode acontecer que no momento em que se queira fazer uso de um recurso, esteja ocupado, �necessidade de esperar �aparecem as filas � Exemplo: nos sistemas de fluxo pode acontecer a formação de filas

Sistemas de fluxo Um fluxo é o movimento de alguma entidade através de um ou mais canais de capacidade finita para ir de um ponto a outro. � Capacidade finita significa que o canal só pode satisfazer a demanda a uma taxa finita. � Exemplos: � �fluxo de automóveis (entidades) através de uma rede de caminhos (canais) �transmissão de mensagens telefônicas (entidades) através da rede (canal)

Sistemas de fluxo � Se dividem em duas classes: �Determinísticos: sistemas no qual o comportamento da demanda de serviço é totalmente previsível, isto é, a quantidade de demanda é exatamente conhecida sobre o intervalo de interesse. �Aleatório: não é possível predizer como vai se comportar a demanda de serviço, por exemplo, o instante de chegada de uma demanda é imprevisível.

Sistemas de fluxo � Exemplo de fluxo determinístico: �Seja r a taxa de chegada (constante) de pacotes em uma rede de comutação a um buffer. �Seja c a taxa (constante) com que esses pacotes são processados em cada nó. �Se r > c, o buffer do nó é inundado com pacotes, já que o número de pacotes em espera de serviço crescerá indefinidamente. �Se r < c, se tem um fluxo estável, o número de pacotes em espera de serviço é finito.

Sistemas de fluxo � Exemplo de fluxo aleatório: �Um centro de computação em que as solicitações de impressão podem chegar em instantes imprevisíveis. �Quando um trabalho de impressão chega, pode ser que o servidor esteja atendendo outro e seja necessário esperar. �Se está desocupado, pode atender imediatamente à nova solicitação de impressão até que esta fique completa.

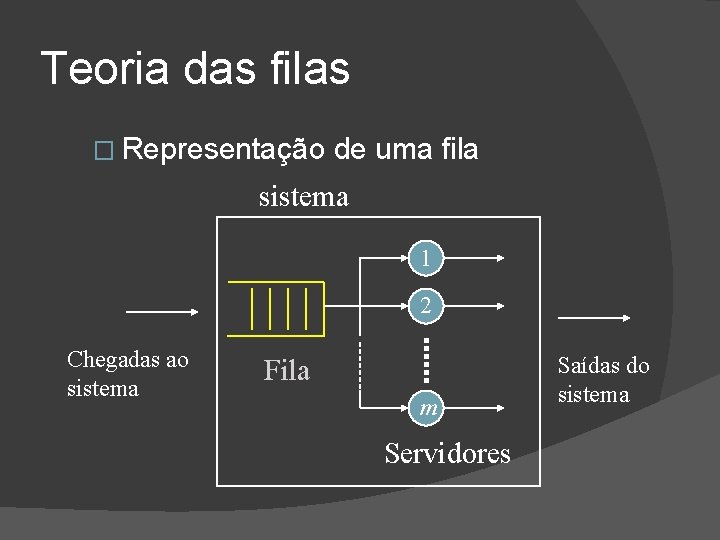
Teoria das filas � Representação de uma fila sistema 1 2 Chegadas ao sistema Fila m Servidores Saídas do sistema

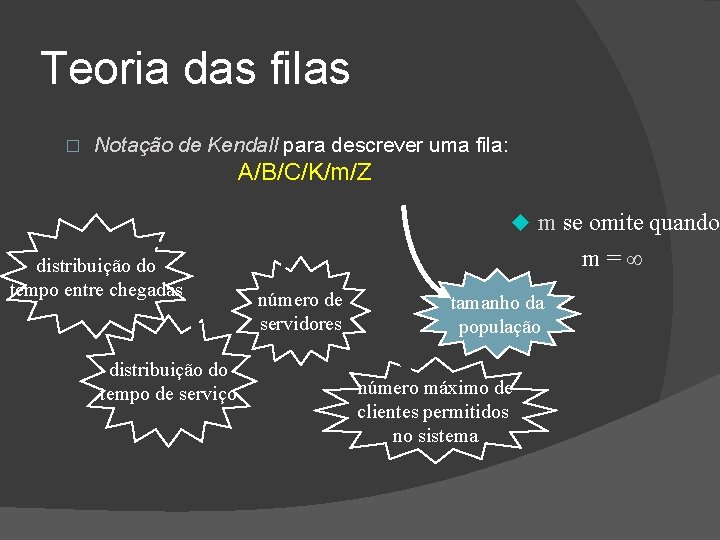
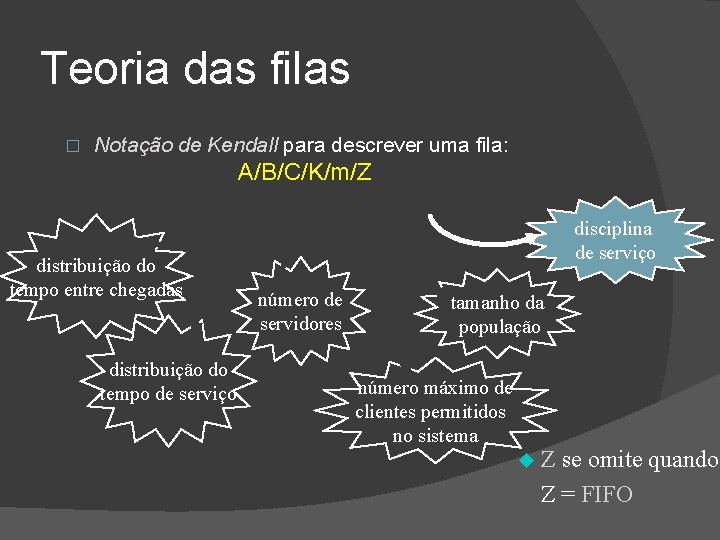
Teoria das filas � Notação de Kendall para descrever uma fila: A/B/C/K/m/Z

Teoria das filas � Notação de Kendall para descrever uma fila: A/B/C/K/m/Z distribuição do tempo entre chegadas u Alguns valores de A mais comuns: M: denota distribuição exponencial equivalente (M provém de Markoviano) G: distribuição geral D: representa um tempo fixo (determinístico)

Teoria das filas � Notação de Kendall para descrever uma fila: A/B/C/K/m/Z distribuição do tempo entre chegadas u distribuição do tempo de serviço Alguns valores de B mais comuns: M: denota distribuição exponencial equivalente (M provém de Markoviano) G: distribuição geral D: representa um tempo fixo (determinístico)

Teoria das filas � Notação de Kendall para descrever uma fila: A/B/C/K/m/Z distribuição do tempo entre chegadas distribuição do tempo de serviço número de servidores

Teoria das filas � Notação de Kendall para descrever uma fila: A/B/C/K/m/Z distribuição do tempo entre chegadas distribuição do tempo de serviço u K é omitido quando: número de servidores K= número máximo de clientes permitidos no sistema

Teoria das filas � Notação de Kendall para descrever uma fila: A/B/C/K/m/Z u m se omite quando: distribuição do tempo entre chegadas distribuição do tempo de serviço m= número de servidores tamanho da população número máximo de clientes permitidos no sistema

Teoria das filas � Notação de Kendall para descrever uma fila: A/B/C/K/m/Z distribuição do tempo entre chegadas distribuição do tempo de serviço disciplina de serviço número de servidores tamanho da população número máximo de clientes permitidos no sistema Z se omite quando: = FIFO u

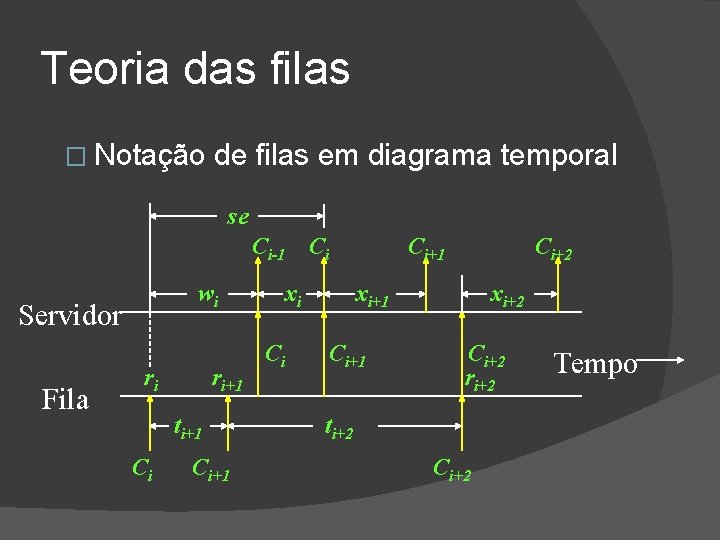
Teoria das filas � Notações usadas nos sistemas de filas: �Ci: i-ésimo usuário que entra ao sistema. �ri: tempo de chegada de Ci �ti: tempo entre as chegadas de Ci-1 e Ci (ti = ri - ri-1) �A(t): distribuição do tempo entre chegadas = P[ti t] �xi: tempo de serviço para Ci �B(x): distribuição do tempo de serviço = P[xi x] �wi: tempo de espera na fila de Ci �se: tempo no sistema (fila mais serviço) de Ci (se = w i + x i)

Teoria das filas � Notação de filas em diagrama temporal se Ci-1 wi Servidor Fila ri ri+1 ti+1 Ci Ci+1 Ci xi Ci Ci+1 Ci+2 xi+1 Ci+1 xi+2 Ci+2 ri+2 ti+2 Ci+2 Tempo

Teoria das filas � Notações usadas nos sistemas de filas (cont. ) �Ek: estado do sistema (normalmente corresponde ao número de usuários no sistema) � k taxa média de chegada dos usuários ao sistema, quando este se encontra no estado k � k: taxa média de serviço quando o sistema se encontra no estado k

Teoria das filas � Outros parâmetros de uma fila: �N(t): número de usuários no sistema no instante t � L = E[k]: número médio de usuários no sistema (em estado estacionário) �LQ: número médio de usuários na fila (em estado estacionário). �T = E[s]: tempo médio de permanência de um usuário no sistema = E[k]/ (fórmula de Little)

CADEIAS DE MARKOV DISCRETAS

Cadeias de Markov discretas � Markov estabeleceu uma simples e útil relação entre as variáveis aleatórias que forman processos estocásticos

Definições � Estado: se Xn= i diz-se que o processo está no estado i no instante n, onde {Xn, n=0, 1, 2. . . } é um processo estocástico que passa por um número finito ou contável de possíveis estados. � Transição: a transição de um estado a outro depende somente do estado atual, e não da história do processo

Observações � No caso das cadeias discretas de Markov, os instantes de tempo nos quais a transição entre um estado e outro acontecem podem asumir apenas valores inteiros 0, 1, 2. . . , n. Em outras palavras, o tempo é discretizado. � Os processos devem permanecer num estado determinado durante um tempo que deve estar geométricamente distribuído.

Observações � Propriedade Markoviana: P{Xn+1 = j | Xn = i, Xn-1= in-1, . . . X 0 = i 0} =P{Xn+1 = j | Xn = i} = Pij 0 � Interpretação (sistema sem memória): A transição de um estado para outro só depende do estado atual, e não da história do processo.

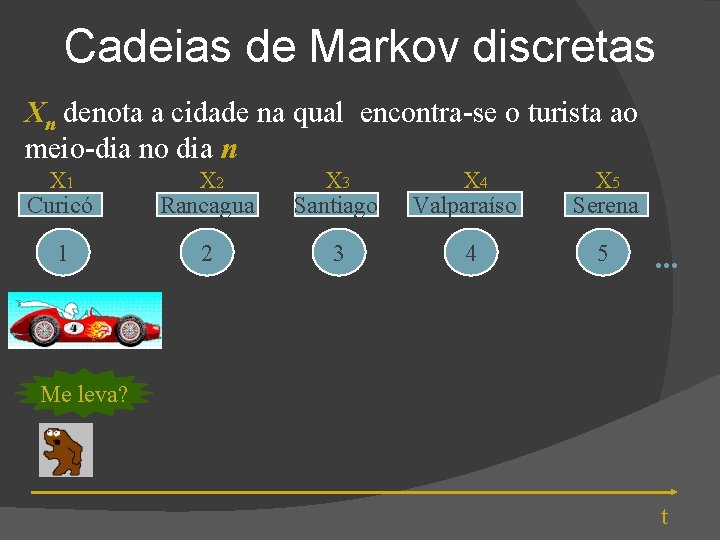
Cadeias de Markov discretas Xn denota a cidade na qual encontra-se o turista ao meio-dia no dia n X 1 Curicó X 2 Rancagua X 3 Santiago X 4 Valparaíso X 5 Serena 1 2 3 4 5 . . . Me leva? t

Cadeias de Markov discretas Curicó Rancagua Santiago Valparaíso Serena 1 2 3 4 5 . . . Me leva? t

Cadeias de Markov discretas Curicó Rancagua Santiago Valparaíso Serena 1 2 3 4 5 . . . Me leva? t

Cadeias de Markov discretas Curicó Rancagua Santiago Valparaíso Serena 1 2 3 4 5 . . . Me leva? t

Cadeias de Markov discretas Curicó Rancagua Santiago Valparaíso Serena 1 2 3 4 5 . . . Continuarei mais ao Norte? t

Cadeias de Markov discretas � Da minha viagem, n posso lhes dizer que: � Nos processos de Markov, o estado atual do sistema e as probabilidades de transição entre os diversos estados caracterizam o comportamento futuro do sistema. � Já que um processo de Markov está num estado determinado, seu comportamento futuro não depende de sua história antes

Definições � Cadeias de Markov são processos estocásticos {X(t)} que satisfazem: � pij: probabilidade de transição do estado i para o estado j depende somente do estado i � P=[pij]: matriz de probabilidade de transição � : tempo em que o processo permanece no estado i, sem memória

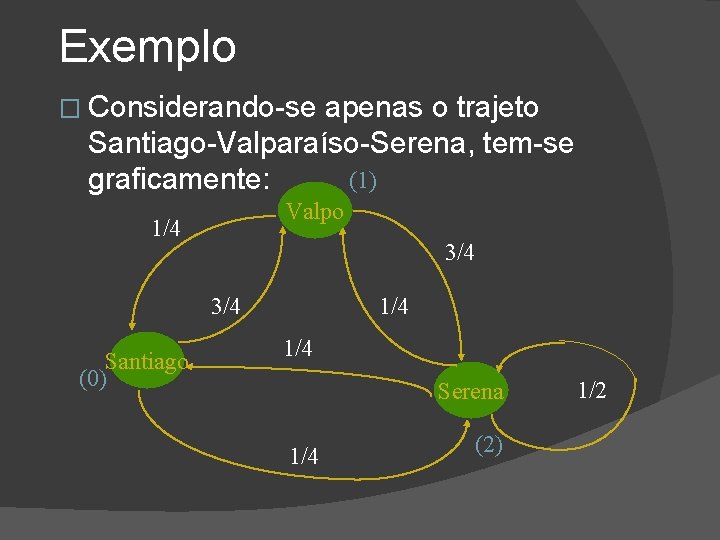
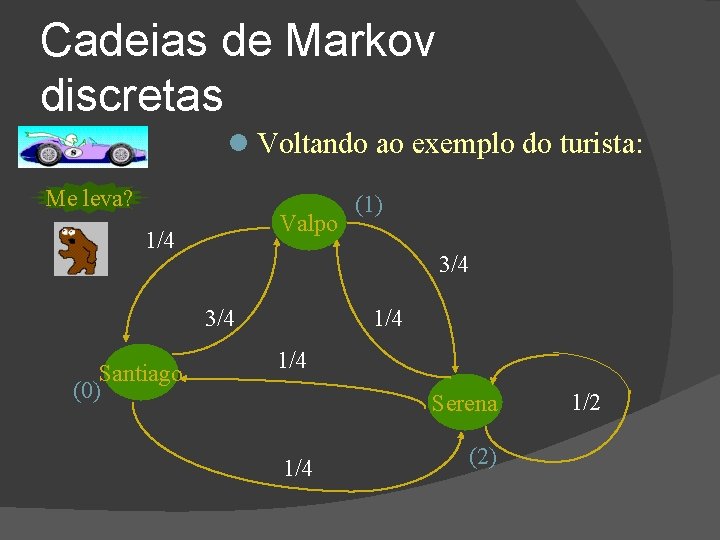
Exemplo � Considerando-se apenas o trajeto Santiago-Valparaíso-Serena, tem-se (1) graficamente: Valpo 1/4 3/4 Santiago (0) 1/4 Serena 1/4 (2) 1/2

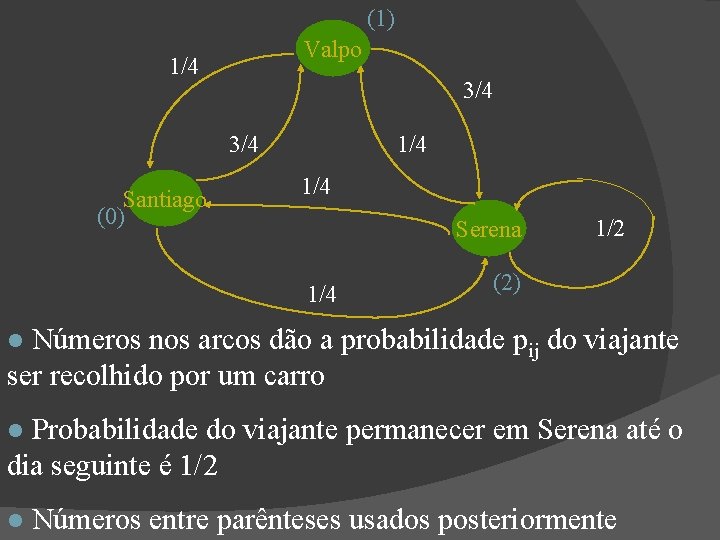
(1) Valpo 1/4 3/4 Santiago (0) 1/4 Serena 1/4 1/2 (2) Números nos arcos dão a probabilidade pij do viajante ser recolhido por um carro Probabilidade do viajante permanecer em Serena até o dia seguinte é 1/2 Números entre parênteses usados posteriormente

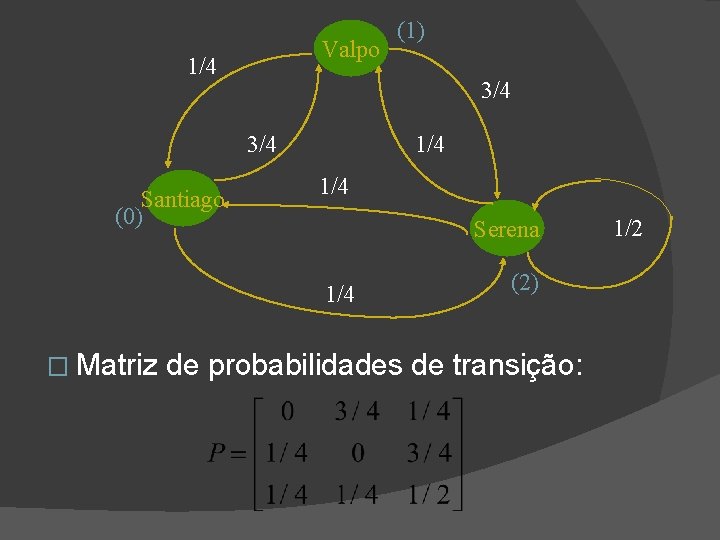
Valpo 1/4 3/4 Santiago (0) 1/4 Serena 1/4 � Matriz (1) (2) de probabilidades de transição: 1/2

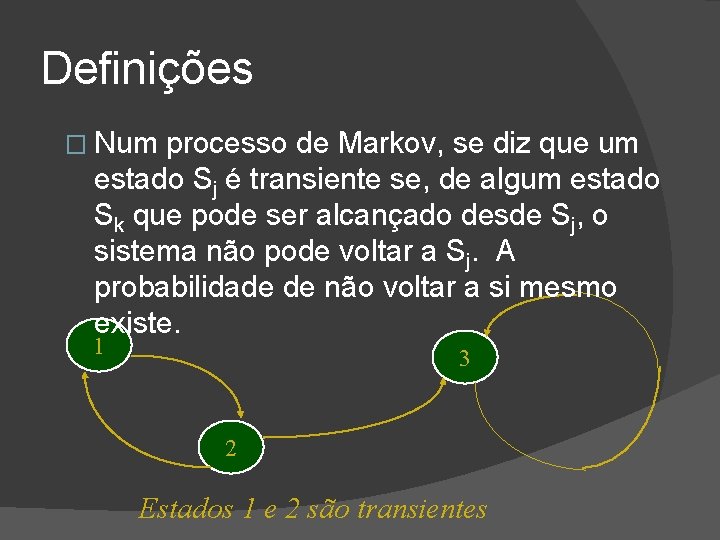
Definições � Num processo de Markov, se diz que um estado Sj é transiente se, de algum estado Sk que pode ser alcançado desde Sj, o sistema não pode voltar a Sj. A probabilidade de não voltar a si mesmo existe. 1 3 2 Estados 1 e 2 são transientes

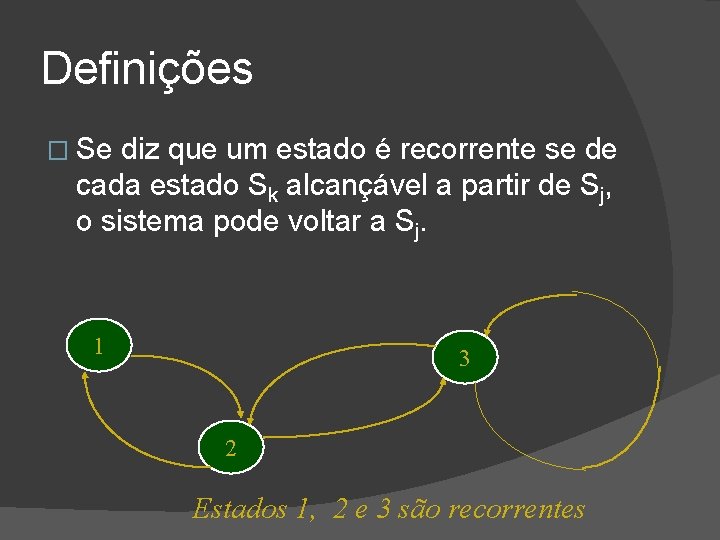
Definições � Se diz que um estado é recorrente se de cada estado Sk alcançável a partir de Sj, o sistema pode voltar a Sj. 1 3 2 Estados 1, 2 e 3 são recorrentes

Cadeias de Markov discretas � Exemplo 1: “predição do tempo” � Dois estados possíveis: 0: chuva 1: não chuva � Hipótese: o tempo amanhã só depende de hoje (processo sem memória) � Chove hoje probabilidade de chover amanhã = � Não chove hoje probabilidade de chover amanhã =

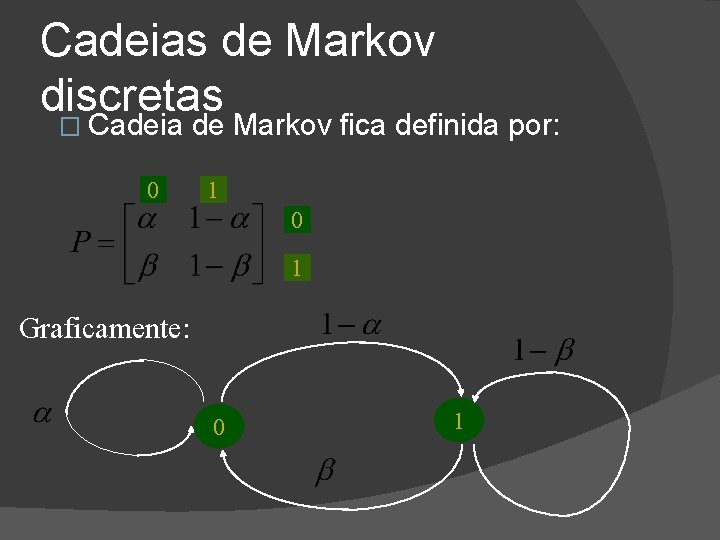
Cadeias de Markov discretas � Cadeia 0 de Markov fica definida por: 1 0 1 Graficamente: 0 1

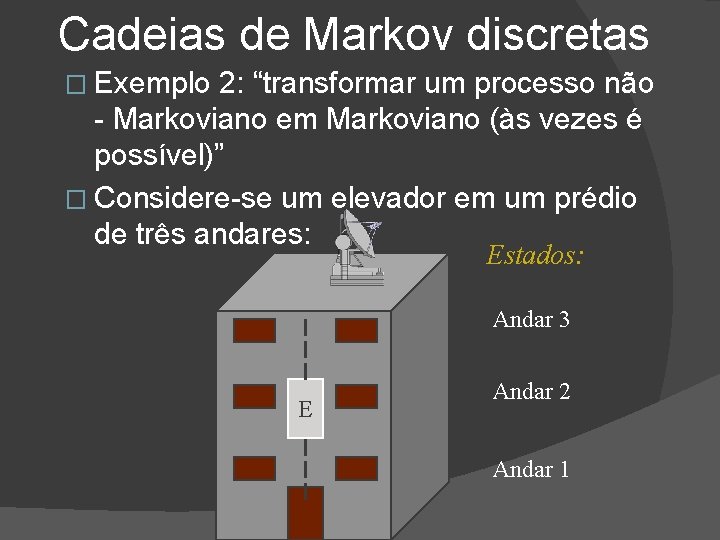
Cadeias de Markov discretas � Exemplo 2: “transformar um processo não - Markoviano em Markoviano (às vezes é possível)” � Considere-se um elevador em um prédio de três andares: Estados: Andar 3 E Andar 2 Andar 1

Cadeias de Markov discretas � Processo não-Markoviano, porque no estado 2 é necessária a informação do estado anterior (1 ou 3) para saber qual será a direção do elevador. � Para que o processo seja Markoviano, se faz necessária uma redefinição dos estados.

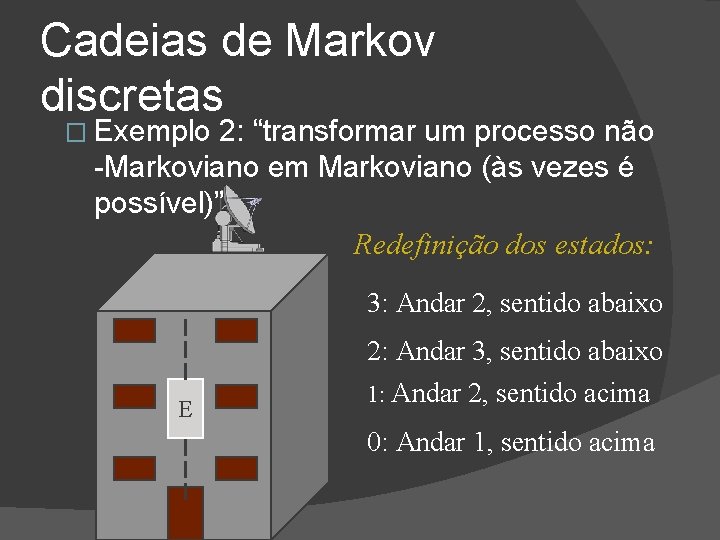
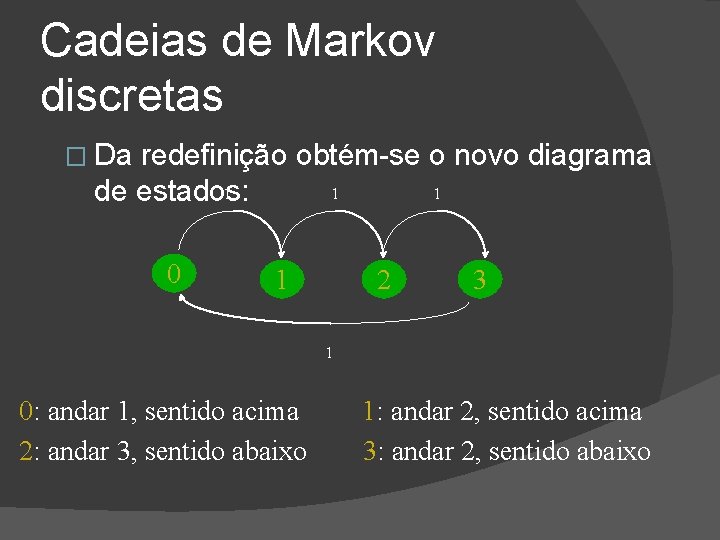
Cadeias de Markov discretas � Exemplo 2: “transformar um processo não -Markoviano em Markoviano (às vezes é possível)” Redefinição dos estados: 3: Andar 2, sentido abaixo E 2: Andar 3, sentido abaixo 1: Andar 2, sentido acima 0: Andar 1, sentido acima

Cadeias de Markov discretas � Da redefinição obtém-se o novo diagrama 1 1 1 de estados: 0 1 2 3 1 0: andar 1, sentido acima 2: andar 3, sentido abaixo 1: andar 2, sentido acima 3: andar 2, sentido abaixo

Cadeias de Markov discretas � Exemplo 2. 1: “transformar um processo não-Markoviano em Markoviano (às vezes é possível)” � Choveu, choveu amanhã choverá: p=0, 7 � Não-choveu, choveu amanhã choverá: p=0, 5 � Choveu, não choveu amanhã choverá: p=0, 4 � Não choveu, não choveu amanhã

Cadeias de Markov discretas � Exemplo 2. 1: “transformar um processo não- Markoviano em Markoviano (às vezes é possível)” � Motivo: há contradição; precisa-se de informação não só do dia presente, mas também do anterior. � Redefinição de estados: se o estado depende do tempo de ontem e hoje então SIM, pode ser Markoviano � Para transformar um processo não. Markoviano em Markoviano (se possível), devem ser redefinidos os estados de

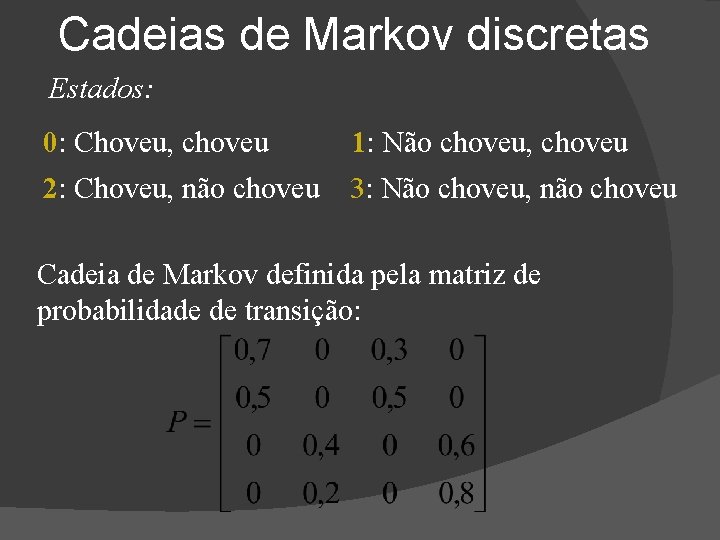
Cadeias de Markov discretas � Exemplo 2. 1: “transformar um processo não- Markoviano em Markoviano (às vezes é possível)” � Portanto, se são redefinidos os seguintes estados: 0: Choveu, choveu 1: Não choveu, choveu 2: Choveu, não choveu 3: Não choveu, não choveu

Cadeias de Markov discretas Estados: 0: Choveu, choveu 1: Não choveu, choveu 2: Choveu, não choveu 3: Não choveu, não choveu Cadeia de Markov definida pela matriz de probabilidade de transição:

Definições � i = probabilidade estacionária de estar no estado i � i(n) = probabilidade de estar no estado I no instante n � i(0) = probabilidade inicial de estar no estado i � =( 0, 1, 2, …, n) � Por definição:

Definições � Exemplo: � Aplicando ou recursivamente:

Definições � Se a cadeia de Markov é irredutível e ergódica, então: existe e é denominada a probabilidade límite de P, ou autovetor esquerdo de P. � Obtenção de :

Cadeias de Markov discretas � Exemplo 3: utilizando o exemplo 1, se a probabilidade de que choverá hoje é 0. 2 e Qual é a probabilidade incondicional de que amanhã choverá?

Cadeias de Markov discretas Aplicando o teorema da probabilidade total: seja a probabilidade incondicional de que choverá amanhã. = P(amanhã choverá | hoje choveu) + P(amanhã choverá | hoje não choveu)

Cadeias de Markov discretas � Exemplo 4: utilizando o exemplo 1 Se e então a probabilidade límite de que choverá é

Cadeias de Markov discretas Voltando ao exemplo do turista: Me leva? Valpo 1/4 3/4 Santiago (0) (1) 1/4 Serena 1/4 (2) 1/2

Cadeias de Markov discretas Do diagrama de estados pode obter-se a matriz de probabilidades de transição definindo-se a matriz de probabilidade como:

Cadeias de Markov discretas Considerando-se a relação obtém-se que com

Cadeias de Markov discretas Resolvendo-se as equações obtém-se as probabilidades em estado de equilíbrio:

CADEIAS DE MARKOV DE TEMPO CONTÍNUO

Cadeias de Markov de tempo contínuo � Definição: uma cadeia de Markov de tempo contínuo é um processo aleatório em que, dado o estado presente, o valor do processo no futuro não depende do passado. �É como uma cadeia de Markov discreta, com a diferença de que o tempo de permanência em um estado é uma variável aleatória com distribuição

Cadeias de Markov de tempo contínuo � Evolução a partir de um estado: : taxa média de saída do estado i para o estado j : taxa média de saída do estado i para o estado k Pij : probabilidade de transitar do estado i ao estado j, no momento da transição

Cadeias de Markov de tempo contínuo � Definição: �tij (tik): tempo de permanência no estado i antes de transitar para j (k), caso passe para j(k). �tij e tik são variáveis aleatórias com distribuição exponencial de parâmetros ij e ik respectivamente. �Seja t o tempo de t = min { tij , tik } permanência no estado i. Do anterior se deduz que : t se distribui exponencialmente com parâmetro ( ij+ ik)

Cadeias de Markov de tempo contínuo � Propriedades: �O tempo de permanência em um estado é Markoviano (processo sem memória) �A escolha do próximo estado se efetua no instante da transição e só depende do estado atual e não do passado, portanto é Markoviano.

Cadeias de Markov de tempo contínuo � Dado que o tempo de permanência em qualquer estado e a escolha do próximo estado são Markovianos, então tem-se uma cadeia de Markov de parâmetro contínuo. � As variáveis aleatórias “tempo de permanência no estado i” e “próximo estado visitado” são independentes.

Cadeias de Markov de tempo contínuo � Definição formal: Um processo aleatório X(t) é uma cadeia de Markov de tempo contínuo se:

Cadeias de Markov de tempo contínuo � Exemplo : processo de Poisson j-i chegadas N(t): estado no instante t N(t): número de chegadas até t

O que é resolver uma cadeia de Markov? �É encontrar as probabilidades de transição de qualquer estado i a qualquer estado j em um dado instante. � Para resolver este problema se utilizará o princípio do balanço global

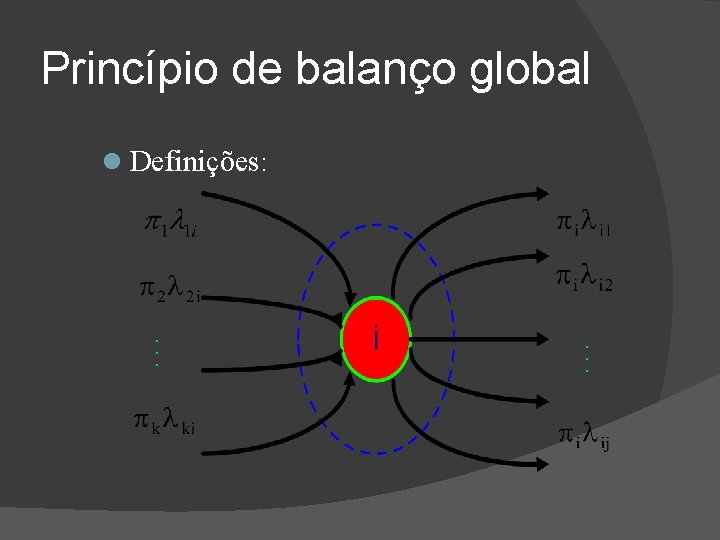
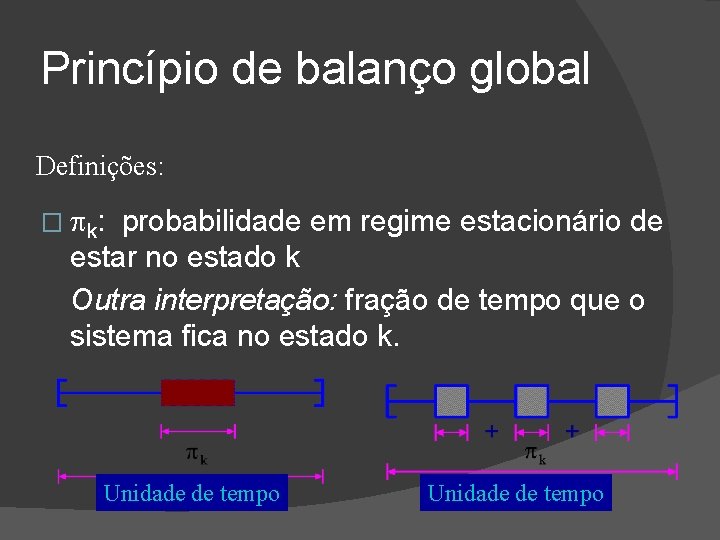
Princípio de balanço global . . . Definições:

Princípio de balanço global Definições: � k: probabilidade em regime estacionário de estar no estado k Outra interpretação: fração de tempo que o sistema fica no estado k. Unidade de tempo

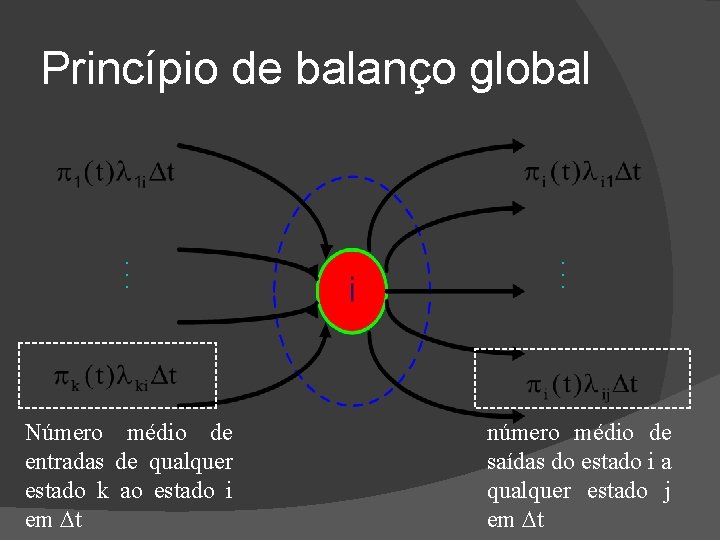
Princípio de balanço global Definições: � k(t): probabilidade de estar no estado k no instante t � ki: taxa média de transição do estado k para o estado i � k· ki: número médio de transições do estado k ao estado i, por unidade

. . . Número médio de entradas de qualquer estado k ao estado i em t . . . Princípio de balanço global número médio de saídas do estado i a qualquer estado j em t

Princípio de balanço global � Número de entradas totais ao estado i em t: � Número de saídas totais desde o estado i em t:

Princípio de balanço global � Balanço de fluxos Entradas líquidas número médio de médias por unidade = entradas totais por - saídas totais por de tempo (EN) unidade de tempo Considerando-se o número de entradas líquidas em um intervalo �t, se tem que:

Princípio de balanço global número de entradas líquidas em t pode ser interpretado como: �O Unidade de tempo

Princípio de balanço global � Usando-se novamente o balanço de fluxos: Variação do tempo de permanência no estado i, por unidade de tempo número de = entradas totais em t número de saídas totais em t Esta variação pode expressar-se em forma da equação de diferenças: (1)

Princípio de balanço global Dividindo por �t em (1): (2) Tomando-se o limite em (2): (3) “ Equação de balanço global para o estado i”

Princípio de balanço global Equação de balanço global para um estado i qualquer: Pode-se reescrever em forma vetorial da seguinte maneira:

Princípio de balanço global Definindo-se:

Equações de balanço global �O conjunto das equações de balanço global pode expressar-se em forma matricial como: Além disso, sempre: “Equações de balanço global”

Equações de balanço global � Em estado estacionário se tem que: fluxo de entrada = fluxo de saída “Equações de balanço global em estado estacionário”

Equações de balanço global � Os conjuntos de equações anteriores servem para resolver tanto a situação transiente como estacionária da cadeia de Markov. Isto é, nos permite encontrar as probabilidades de transição de qualquer estado i a qualquer estado j num intervalo t qualquer (Pij(t)).

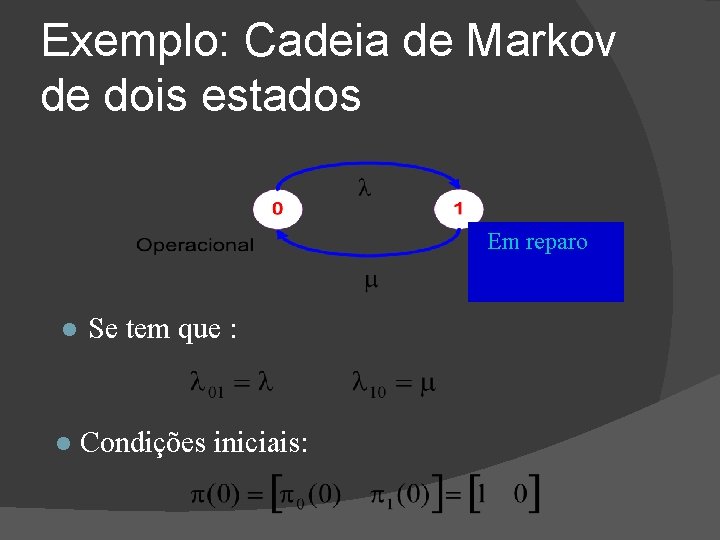
Exemplo: Cadeia de Markov de dois estados � Uma máquina funciona uma quantidade de tempo exponencialmente distribuída com média 1/ Quando falha se repara com a mesma distribuição em um tempo médio 1/. Inicialmente, a máquina encontra-se funcionando. � Deseja-se determinar a probabilidade de que a máquina esteja funcionando em um instante t dado. Inicialmente a máquina se encontra operacional.

Exemplo: Cadeia de Markov de dois estados Em reparo Se tem que : Condições iniciais:

Exemplo: Cadeia de Markov de dois estados � Equações de balanço global estabelecem que: Forma escalar da equação anterior é:

Exemplo: Cadeia de Markov de dois estados � Portanto: (4) (5) (6)

Exemplo: Cadeia de Markov de dois estados Resolvendo (4), (5) e (6), obtém-se:

Exemplo: Cadeia de Markov de dos estados � Resolvendo em estado estacionário, obtém-se: (7) (8) (9)

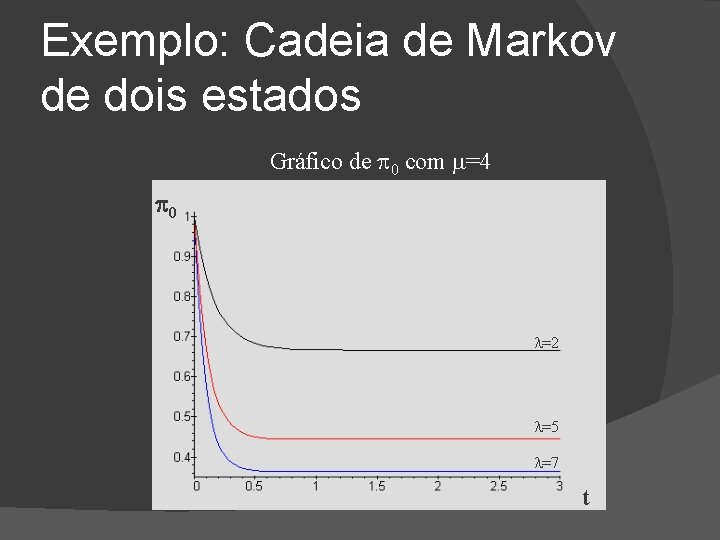
Exemplo: Cadeia de Markov de dois estados � Resolvendo (7), (8) e (9), obtém-se : Observação: Também pode chegar-se a este resultado através das equações em estado transiente, fazendo tender o parâmetro t a infinito.

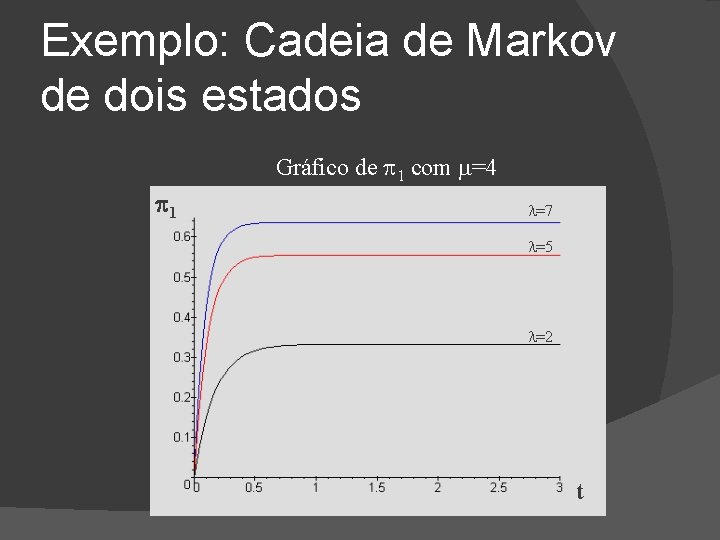
Exemplo: Cadeia de Markov de dois estados Gráfico de 0 com =4 0 =2 =5 =7 t

Exemplo: Cadeia de Markov de dois estados Gráfico de 0 com =4 0 =7 =5 =2 t

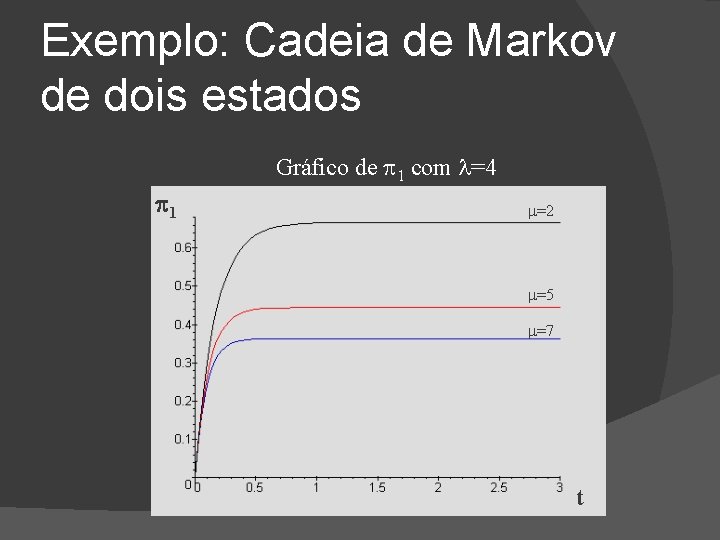
Exemplo: Cadeia de Markov de dois estados Gráfico de 1 com =4 1 =7 =5 =2 t

Exemplo: Cadeia de Markov de dois estados Gráfico de 1 com =4 1 =2 =5 =7 t

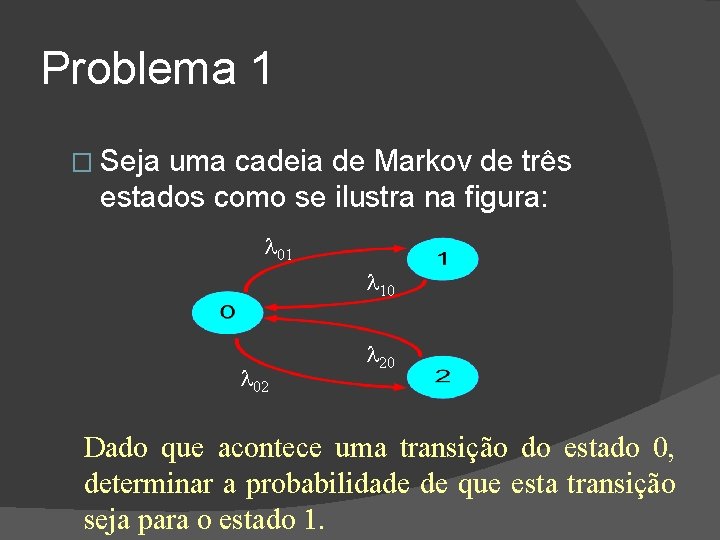
Problema 1 � Seja uma cadeia de Markov de três estados como se ilustra na figura: 01 10 02 20 Dado que acontece uma transição do estado 0, determinar a probabilidade de que esta transição seja para o estado 1.

Problema 1 � Define-se: �t 01: tempo de permanência no estado 0 antes de transitar para o estado 1, caso transite para o estado 1 �t 02: tempo de permanência no estado 0 antes de transitar para o estado 2, caso transite para o estado 2 �A probabilidade pedida é equivalente à probabilidade de que a transição para o estado 1 ocorra antes da transição para o

Problema 1 � Portanto:

Problema 1 � Estendendo o resultado anterior, para qualquer número de estados, se tem que: onde Pij: probabilidade de transitar do estado i para o estado j, dado que acontece uma transição ik: taxa média de saída do estado i para o estado k

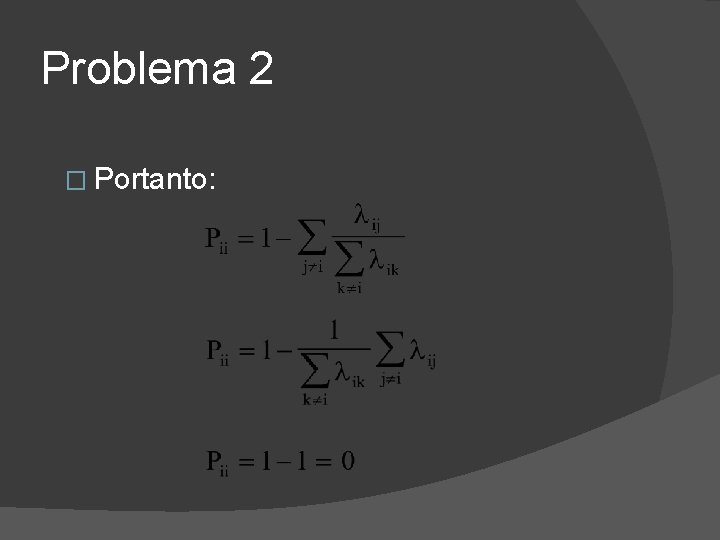
Problema 2 � Dado que aconteceu uma transição do estado i, qual é a probabilidade de que o próximo estado seja i ? Sabe-se que: Além disso:

Problema 2 � Portanto:

Problema 3 � Dado que no instante zero o sistema está no estado i, qual é a probabilidade de permanecer neste estado até o instante t? P{permanecer em estado i até t} = 1 - P{sair do estado i até t} Dado que o tempo de permanência é exponencial: Portanto: P{sair do estado i até t} P{permanecer no estado i até t}