Sveuilite u Splitu Pomorski fakultet Fourierova analiza signala












































- Slides: 57

Sveučilište u Splitu Pomorski fakultet Fourierova analiza signala Joško Šoda

Sažetak izlaganja: • Podjela signala • Fourierov niz • Fourierov integral • Uzorkivanje signala • Frekvencijski odziv kod diskretnih sekvenci • Diskretna Fourierova transformacija • Zaključak

Ciljevi: • predstaviti temeljne vrste signala • predstaviti temelje spektralne analize signala • predstaviti i razlikovati tri vrste spektralne analize signala (Fourierov niz, Fourierov integral i diskretnu fourierovu transformaciju)

Podjela signala

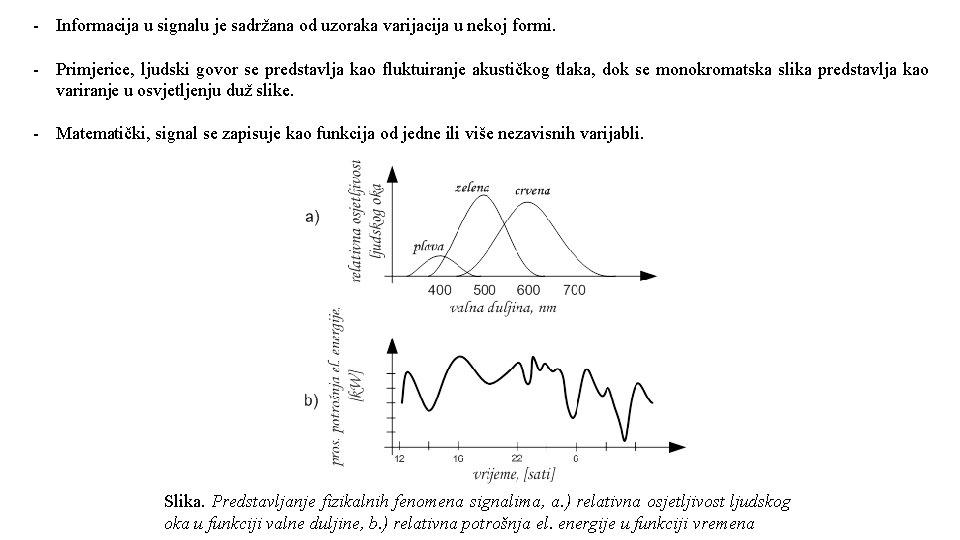
- Informacija u signalu je sadržana od uzoraka varijacija u nekoj formi. - Primjerice, ljudski govor se predstavlja kao fluktuiranje akustičkog tlaka, dok se monokromatska slika predstavlja kao variranje u osvjetljenju duž slike. - Matematički, signal se zapisuje kao funkcija od jedne ili više nezavisnih varijabli. Slika. Predstavljanje fizikalnih fenomena signalima, a. ) relativna osjetljivost ljudskog oka u funkciji valne duljine, b. ) relativna potrošnja el. energije u funkciji vremena

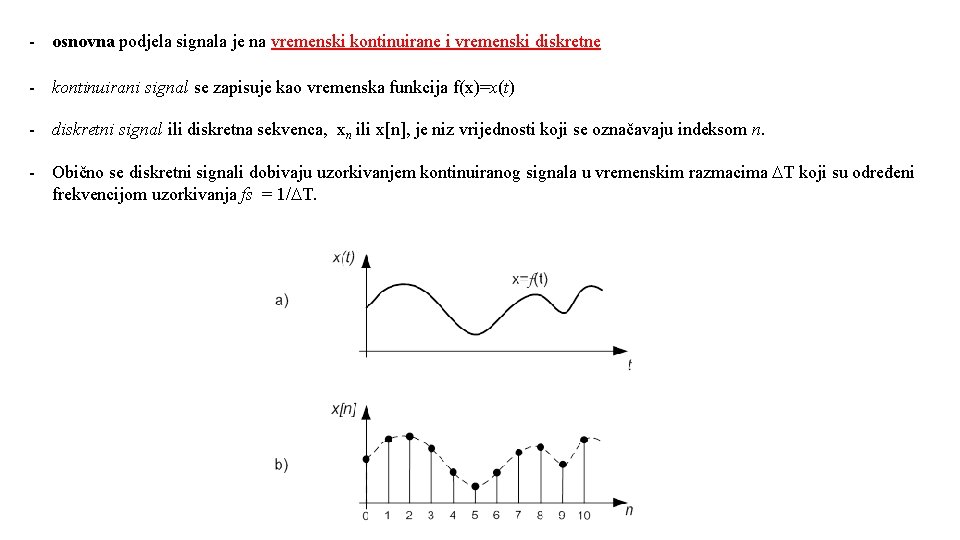
- osnovna podjela signala je na vremenski kontinuirane i vremenski diskretne - kontinuirani signal se zapisuje kao vremenska funkcija f(x)=x(t) - diskretni signal ili diskretna sekvenca, xn ili x[n], je niz vrijednosti koji se označavaju indeksom n. - Obično se diskretni signali dobivaju uzorkivanjem kontinuiranog signala u vremenskim razmacima T koji su određeni frekvencijom uzorkivanja fs = 1/ T.

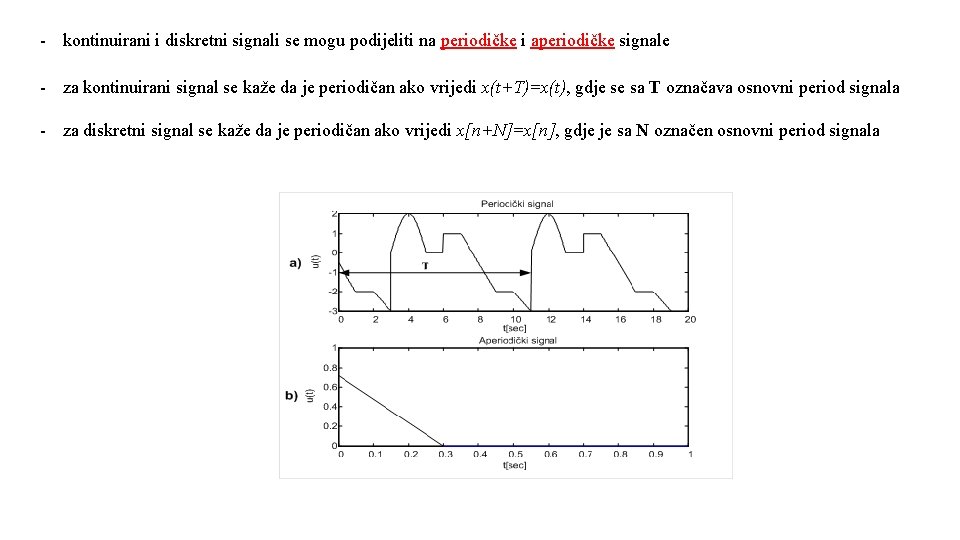
- kontinuirani i diskretni signali se mogu podijeliti na periodičke i aperiodičke signale - za kontinuirani signal se kaže da je periodičan ako vrijedi x(t+T)=x(t), gdje se sa T označava osnovni period signala - za diskretni signal se kaže da je periodičan ako vrijedi x[n+N]=x[n], gdje je sa N označen osnovni period signala

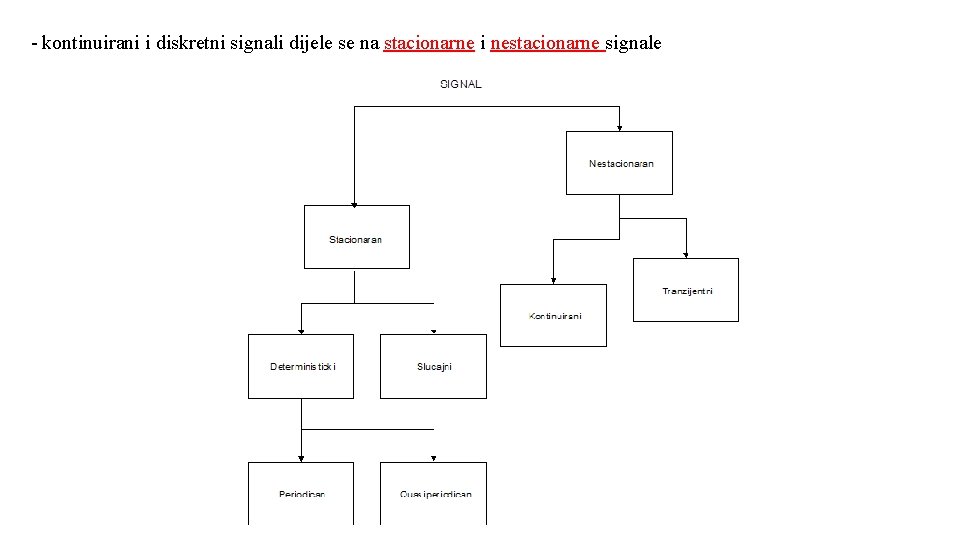
- kontinuirani i diskretni signali dijele se na stacionarne i nestacionarne signale

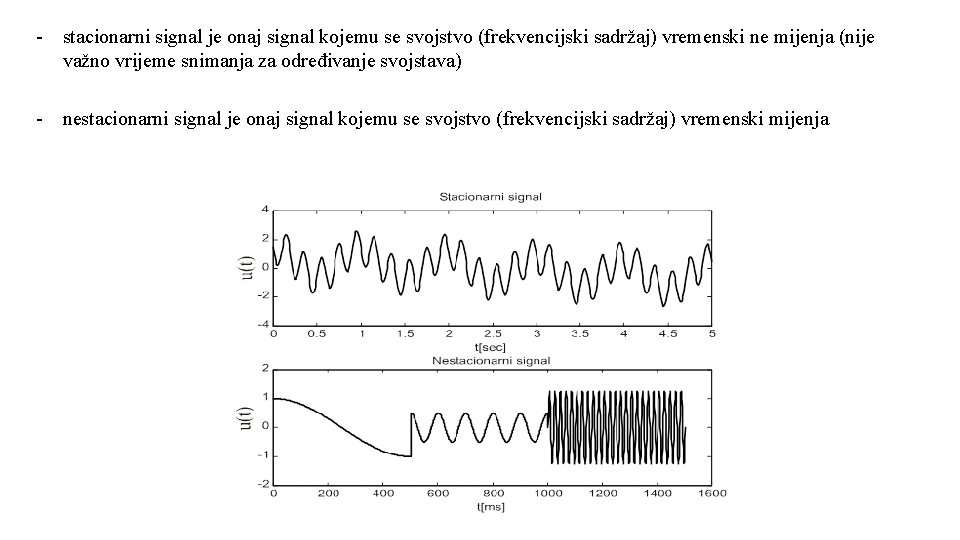
- stacionarni signal je onaj signal kojemu se svojstvo (frekvencijski sadržaj) vremenski ne mijenja (nije važno vrijeme snimanja za određivanje svojstava) - nestacionarni signal je onaj signal kojemu se svojstvo (frekvencijski sadržaj) vremenski mijenja

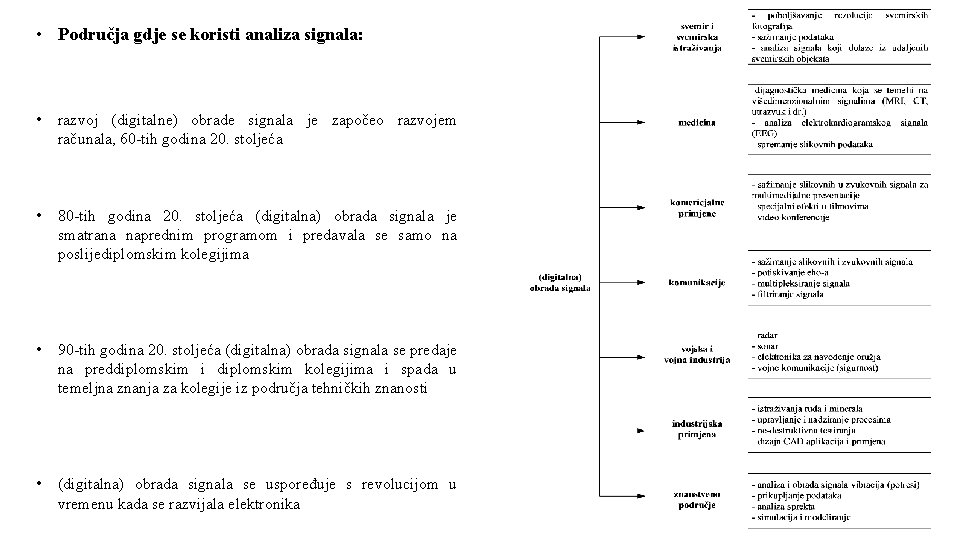
• Područja gdje se koristi analiza signala: • razvoj (digitalne) obrade signala je započeo razvojem računala, 60 -tih godina 20. stoljeća • 80 -tih godina 20. stoljeća (digitalna) obrada signala je smatrana naprednim programom i predavala se samo na poslijediplomskim kolegijima • 90 -tih godina 20. stoljeća (digitalna) obrada signala se predaje na preddiplomskim i diplomskim kolegijima i spada u temeljna znanja za kolegije iz područja tehničkih znanosti • (digitalna) obrada signala se uspoređuje s revolucijom u vremenu kada se razvijala elektronika

Načini analize signala: • vremensko područje (korelacija, autokorelacija i dr. ) • frekvencijsko područje (Fourierov niz, Fourierov integral, Diskretna Fourierova transformacija, FFT) • vremensko – frekvencijsko područje (prozorska Fourierova transformacija, valići, Winger-Villeova transformacija, Huan-Huangova transformacija, kompleksni valići, i dr. ) • statistička obrada signala (slučajne varijable, varijanca, očekivanja, momenti, i dr. ) • Svrha analize signala: dobiti dodatne informacije o proučavanom signalu.

Fourierova analiza

- dobila je ime po francuskom matematičaru i fizičaru Jean Baptiste Joseph Fourier (1768 – 1830) - Fourier je 1807. godine promatrao propagaciju topline, te je predložio da se sinusoidalne (koje se matematički opisuju preko kompleksne eksponencijale) funkcije koriste za opisivanje raspodjele temperature. - Fourier je tvrdio da se bilo koji periodički signal može predstaviti sumom sinusoidalnih funkcija određene frekvencije i njenih višekratnika. - Fourierova analiza jedan je od najznačajnijih alata kod obrade signala i analize sustava!!!

- 1759. J. L. Lagrange je kritizirao ideju korištenja trigonometrijskih funkcija jer je iznio primjedbu da u točkama diskontinuiteta nije moguće točno opisati zadani signal (Gibbsov fenomen) - P. L. Dirichlet (1829. ) je proširio analizu uzimajući u obzir uvjete na granici, te predstavio pravila s kojima se periodički signal može opisati Fourierovim nizom i pod kojim uvjetima (tzv. Dirichletovi uvjeti) - 1822. godine Fourier je napokon predstavio svoj rad (prije nije mogao biti objavljen zbog protivljenja Lagrangea) „Theorie analytique de la chaleur” (eng. „The Analytical Theory of Heat”)

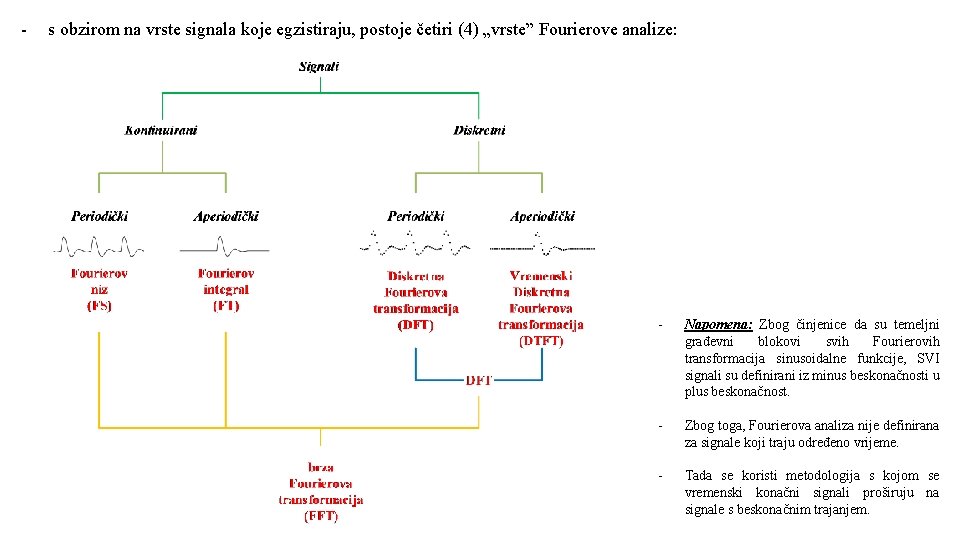
- s obzirom na vrste signala koje egzistiraju, postoje četiri (4) „vrste” Fourierove analize: - Napomena: Zbog činjenice da su temeljni građevni blokovi svih Fourierovih transformacija sinusoidalne funkcije, SVI signali su definirani iz minus beskonačnosti u plus beskonačnost. - Zbog toga, Fourierova analiza nije definirana za signale koji traju određeno vrijeme. - Tada se koristi metodologija s kojom se vremenski konačni signali proširuju na signale s beskonačnim trajanjem.

• Fourierov niz - Hipoteza: svaki periodički signal može se prikazati u frekvencijskom području preko jakosti (magnitude) i faze. - Vrijedi: ako je promatrani signal kontinuiran i periodički u vremenskom području, tada je diskretan u frekvencijskom području i obratno!!! - Svaki periodički signal se može predstaviti jednadžbom: aperiodički signal

- U DSP terminologiji - Upravo navedeno svojstvo se koristi kod DSP procesora, tj. svaki promatrani odsječak signala koji se obrađuje, tretira se kao periodički, te se temeljem toga računaju koeficijenti!!! - koristeći kompleksnu eksponencijalu, periodički signal se može zapisat: se naziva periodičko proširenje od x(t) - koeficijenti

- koristeći matematičke operacije: množenja lijeve i desne strane s kompleksnom eksponencijalom i integriranja te sređivanjem izraza dobiva se izraz za računanje koeficijenata periodičkog signala: - Dakle, tzv. polarni oblik Fourierovog niza, tj. formule analize i sinteze glase: • formule analize • formula sinteze

- općenito radi se o kompleksnom broju koji se može predstaviti kao: - Primjer: Neka je zadan koji je periodičan za: ili


Polarni oblik Fourierovog niza se može prikazati u trigonometrijskom obliku ako se preradi na slijedeći način: uz supstitucije:

Sređivanjem gore navedenih izraza dobiva se trigonometrijski oblik Fourierovog niza ili tzv. Euler ili Euler – Fourierova jednadžba za predstavljanje periodičkih sekvenci koja glasi: Trigonometrijski oblik Fourierovog niza


Konvergencija Fourierovog niza - Postavlja se pitanje za koje sve periodičke signale se može koristiti Fourierov niz? - U praksi može se dogoditi da ima beskonačno mnogo koeficijenta s kojima bi se trebao predstaviti promatrani periodički signal da bude identičan polaznom signalu. - Također, može se dogoditi da iako su svi koeficijenti konačni da razvoj u Fourierov red daje divergenciju, tj. ne teži funkciji x(t). - Postoje dvije klase uvjeta koje periodički signal mora zadovoljiti da bi se mogao prikazati Fourierovim nizom. - Ti uvjeti su poznati pod nazivom Dirichletovi uvjeti.

Dirichletovi uvjeti: 1. Periodički signali moraju imati konačnu energiju u jednom periodu, tj. vrijedi: Ako je gore navedeni uvjet zadovoljen koeficijenti od su konačni. To znači, da ako bi se izračunala energija od x(t) i energija od rekonstruiranog signala, da bi razlika energija težila nuli kada bi broj koeficijenata težio k beskonačnosti. Tj. energije rekonstruiranog i originalnog signala bi bile jednake. 2. U bilo kojem konačnom intervalu ako postoji konačan broj diskontinuiteta, tada se Fourierovim nizom predstavlja originalni signal, osim u točkama diskontinuiteta. U diskontinuitetima se uzima srednja vrijednost kao vrijednost prekida. Valja istaći da signali koji su nedefinirani u nekom periodu, u praksi nisu fizički mogući!

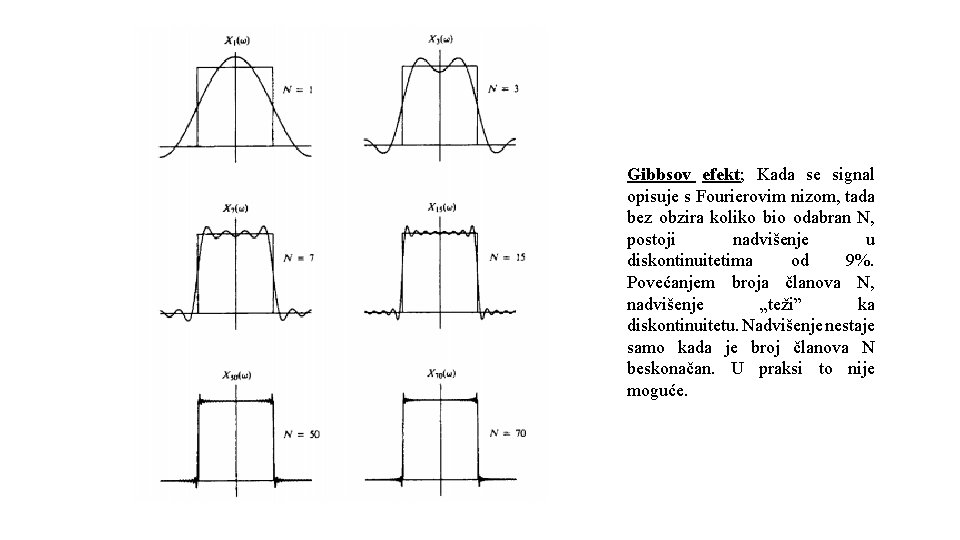
Gibbsov efekt; Kada se signal opisuje s Fourierovim nizom, tada bez obzira koliko bio odabran N, postoji nadvišenje u diskontinuitetima od 9%. Povećanjem broja članova N, nadvišenje „teži” ka diskontinuitetu. Nadvišenje nestaje samo kada je broj članova N beskonačan. U praksi to nije moguće.


Fourierova transformacija ili Fourierov integral • Za aperiodičke signale potrebno je razviti novi alat, tj. novu tehniku analize. • Metodologija razvoja je slijedeća: Aperiodički signal se predstavi kao periodički, dakle, tretira ga se kao periodički signal s osnovnim periodom koji teži u beskonačnost. • Vrijedi zaključak: Ako se primjeni Fourierov red na periodički signal, te se dopusti da transformacija aperiodičkog signala. Također kada je tada vrijedi: i , dobiva se.

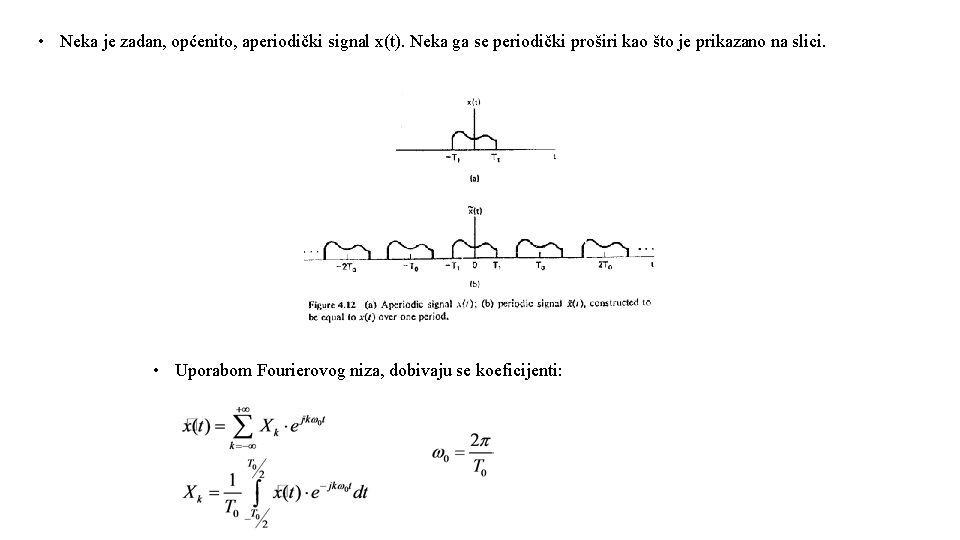
• Neka je zadan, općenito, aperiodički signal x(t). Neka ga se periodički proširi kao što je prikazano na slici. • Uporabom Fourierovog niza, dobivaju se koeficijenti:

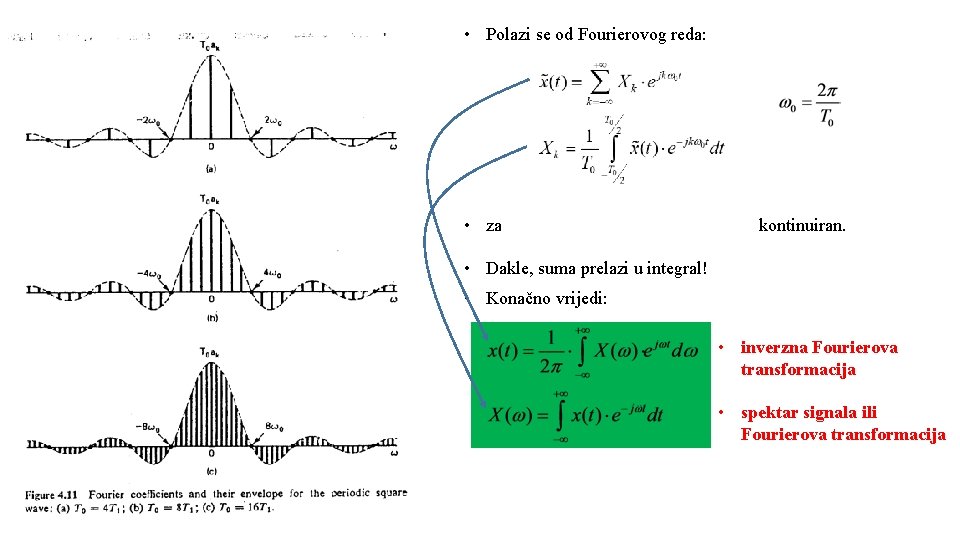
• Polazi se od Fourierovog reda: • za kontinuiran. • Dakle, suma prelazi u integral! • Konačno vrijedi: • inverzna Fourierova transformacija • spektar signala ili Fourierova transformacija

• Svojstva Fourierove transformacije

• Svojstvo simetrije • Ako je x(t) realna funkcija, tada vrijedi: • Dokaz: • Kod realnih funkcija vrijedi: • Dobiva se:

• Gustoća energije kod aperiodičkog signala, Parsevalov teorem • Gustoća energije kod aperiodičkog signala se može izračunati iz općenite formule za energiju signala u vremenskom području: • Energija signala se može predstaviti: • Ako se uvrsti formula za Fourierovu transformaciju tada vrijedi:

• Sređivanjem izraza, dobiva se: • Kod realnih sekvenci, vrijedi: • Parsevalov teorem kaže da se energija signala može računati u vremenskom području kao kvadrat modula koeficijenata signala u vremenu ili kao gustoća energije spektra, odnosno kvadrat modula spektra magnitude signala u frekvencijskom području.

• Svojstvo konvolucije signala u frekvencijskom području • Ako su zadani signal ulaza x(t), prijenosna funkcija sustava h(t) i izlazni signal y(t), tada se izlazni signal y(t) može izračunati prema formuli za konvoluciju signala: • Spektar izlaznog signala se računa prema: • Konvolucija u vremenskom području odgovara množenju spektra signala u frekvencijskom području!!!


• Uzorkivanje signala • Vremensko uzorkivanje je proces pretvaranja vremenski – kontinuiranog signala u vremenski – diskretnu sekvencu. • Razvojem digitalne tehnike razvili su se i A/D pretvarači. • Proces uzorkivanja će biti dobiven uporabom korištenjem Fourierove analize, odnosno spektra signala.

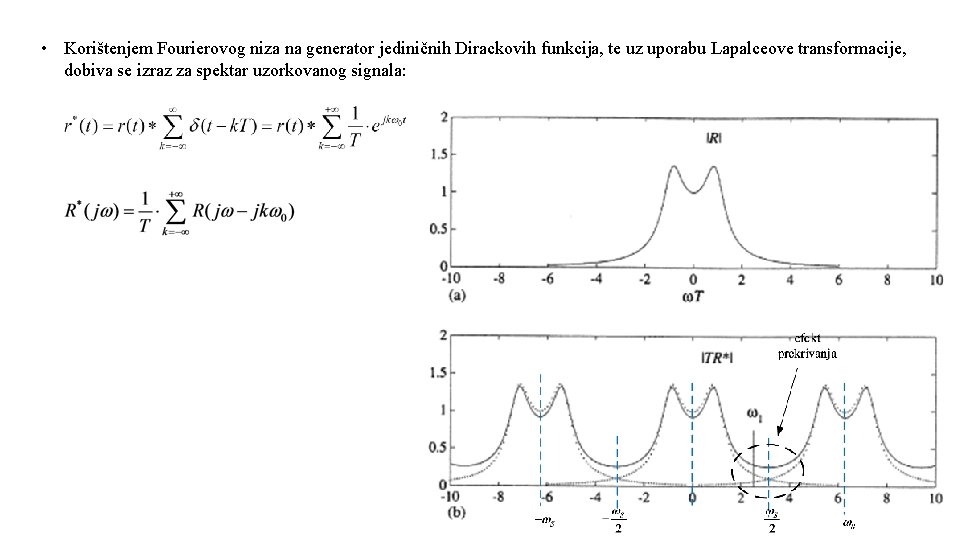
• Korištenjem Fourierovog niza na generator jediničnih Dirackovih funkcija, te uz uporabu Lapalceove transformacije, dobiva se izraz za spektar uzorkovanog signala:

• Dakle, kada se signal r(t) uzorkuje, tada se u spektru na mjestima uzorkivanja pojavi spektar od originalnog signala. • Također, tijekom uzorkivanja posebna pozornost se treba voditi kod izbora frekvencije uzorkivanja. • Ako se frekvencija uzorkivanja ne odabere ispravno može doći do efekta prekrivanja (eng. aliasing). • Također, u praksi je poznato da spektar signala ne mora biti konačan. Zbog toga iako je izabrana ispravna frekvencija uzorkivanja može doći do efekta prekrivanja. Da bi se to izbjeglo, u praksi, se prije uzorkivanja postavi NF pred-filtar s kojim se spektar originalnog signala ogranići.

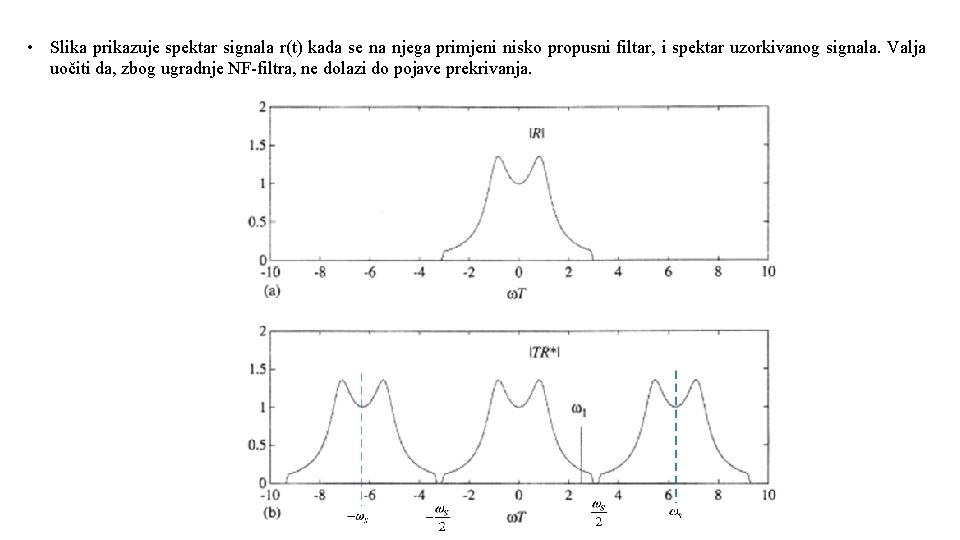
• Slika prikazuje spektar signala r(t) kada se na njega primjeni nisko propusni filtar, i spektar uzorkivanog signala. Valja uočiti da, zbog ugradnje NF-filtra, ne dolazi do pojave prekrivanja.

• Teorem uzorkivanja: Signal r(t) se može obnoviti iz uzoraka ako je frekvencija uzorkivanja barem dva puta veća od najveće frekvencije (gornje granične frekvencije) signala r(t). • Matematički zapis teorema uzorkivanja: Spektar uzorkivanog signala i teorem uzorkivanja

• Frekvencijski odziv kod diskretnih sekvenci (signala) • Važno svojstvo svakog vremenski nezavisnog sustava (LTI sustava) je odziv u ustaljenom stanju ako se na ulazu sustava narine sinusoidalna sekvenca, kao što je prikazano na slici. • Sinusoidalna sekvenca se može prikazati preko kompleksne eksponencijalne sekvence, koristeći Eulerove relacije: - digitalna frekvencija - period kontinuiranog signala - Ponavljanje: - period uzorkivanja

• Uzimajući u obzir da se s kompleksnom eksponencijalom može prikazati i DC komponenta, na način da se digitalna frekvencija postavi na vrijednost nula, kaže se da kompleksna eksponencijala predstavlja karakterističnu funkciju (eng. eigenfunction). • Dakle, s karakterističnom funkcijom se može izračunati odziv sustava u ustaljenom stanju, na način:

• Neka je zadan diskretni sustav kao što je prikazano na slici. • Izlaz y[n] iz sustava se može dobiti primjenom konvolucijske sume

• Ako se na ulaz sustava dovede karakteristična funkcija , za odziv se dobiva: • Ako se na ulaz promatranog sustava narine karakteristična funkcija, na izlazu se dobiva odziv sustava u ustaljenom stanju. • Odziv sustava u ustaljenom stanju je jednak karakterističnoj funkciji pomnoženo s karakterističnom vrijednosti (eng. eigenvaule or characteristic value).

• Karakteristična vrijednost, SUSTAVA. ima značajnu ulogu u obradi signala, te se naziva FREKVENCIJSKI ODZIV • Dakle, ako se na ulaz sustava dovede karakteristična funkcija, na izlazu sustava se dobije odziv sustava u ustaljenom stanju, preko frekvencijskog odziva, kao što je prikazano na slici.

• Svojstva frekvencijskog odziva • Kao što se može vidjeti frekvencijski odziv je kompleksna funkcija te se može pisati: - magnituda - faza ili kut • Dakle, ako se promatraju magnituda i faza kod različitih frekvencija, dobiva se frekvencijski odziv sustava.

• Primjer: Neka je zadan sustav: . Ako se na ulazu narine karakteristična funkcija potrebno je pronaći i nacrtati frekvencijski odziv sustava. • Rješenje:

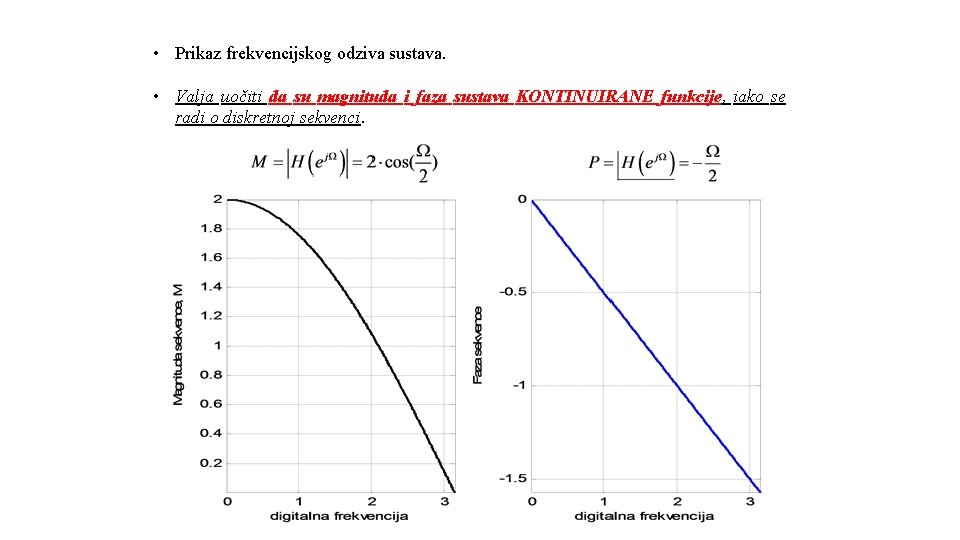
• Prikaz frekvencijskog odziva sustava. • Valja uočiti da su magnituda i faza sustava KONTINUIRANE funkcije, iako se radi o diskretnoj sekvenci.

• Periodičnost • Funkcija je periodička u periodu ! • Dokaz: • Simetričnost • Magnituda od je parna funkcija od digitalne frekvencije, dok je faza od je neparna funkcija od digitalne frekvencije. • Dokaz:

• Zaključak: - parna funkcija - neparna funkcija

• Frekvencijski opseg • Zbog činjenice da je digitalna frekvencija periodička funkcija, i koristeći spoznaje iz teorema uzorkivanja, maksimalna digitalna frekvencija kod koje ne dolazi do tzv. efekta prekrivanja je: • Ako se uvrste vrijednosti za digitalnu frekvenciju, tada vrijedi: • Dakle, maksimalna analogna frekvencija koju se može razlučiti u sustavu, koji je uzorkivan s frekvencijom uzorkivanja, iznosi pola frekvencije uzorkovanja! Dakle, odabir frekvencija uzorkivanja ima značajnu ulogu kod frekvencijskog odziva diskretnih sekvenci.

• Diskretna Fourier-ova transformacija • Polazna točka je da se bilo koja sekvenca može predstaviti kao suma kompleksnih eksponencijala. • Također, konačna sekvenca se može periodički proširiti, te na taj način se polazna točka može primijeniti. • Jednadžbe Diskretne Fourier-ove transformacije, DFT, glase:

• Primjer: Za sekvencu prikazanu na slici potrebno je pronaći DFT transformaciju, te magnitudu i fazu prikazati grafički. • Rješenje:

• Zaključak • Fourierova analiza signala pretvara promatrani signal iz vremenskog područja u frekvencijsko područje (iz amplituda-vrijeme prostora u magnituda-frekvencija prostor) • osim proučavanja signala, s Fourierovom analizom se proučavaju i regulacijski sustavi • kompleksne eksponencijale (sinusna i kosinusna funkcija) su građevni blokovi Fourierove transformacije • brza Fourierova transformacija (FFT) je algoritam koji se danas koristi za računanje spektra i diskretnih i „kontinuiranih” signala


Sveučilište u Splitu Pomorski fakultet Fourierova analiza signala Joško Šoda
 Digitalna obrada signala
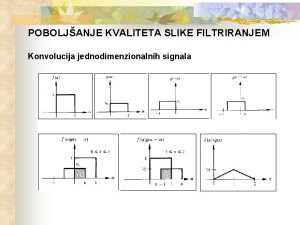
Digitalna obrada signala Konvolucija
Konvolucija Atenski pomorski savez
Atenski pomorski savez Pomorski agent posao
Pomorski agent posao Pomorski azimut
Pomorski azimut Ekonomski fakultet podgorica
Ekonomski fakultet podgorica Grf
Grf Poljoprivredni fakultet predmeti
Poljoprivredni fakultet predmeti Ekonometrija
Ekonometrija Poljoprivredni fakultet zagreb
Poljoprivredni fakultet zagreb Fakultet za računarske nauke i informatiku ljubljana
Fakultet za računarske nauke i informatiku ljubljana Poslovni fakultet
Poslovni fakultet Visoka medicinska skola bitola profesori
Visoka medicinska skola bitola profesori Fakultet za psihologija skopje
Fakultet za psihologija skopje Matematisk naturvitenskapelig fakultet uib
Matematisk naturvitenskapelig fakultet uib Nuklearna fizika fakultet
Nuklearna fizika fakultet Pravni fakultet zagreb socijalni rad
Pravni fakultet zagreb socijalni rad Ekonomski fakultet u tuzli
Ekonomski fakultet u tuzli Filozofski fakultet nikšić
Filozofski fakultet nikšić Slobodan navalusic
Slobodan navalusic Medicinski fakultet banja luka
Medicinski fakultet banja luka Dif fakultet skopje
Dif fakultet skopje Medicinski fakultet zagreb predmeti
Medicinski fakultet zagreb predmeti Ekonomski fakultet banja luka
Ekonomski fakultet banja luka Realfagskonferansen 2021
Realfagskonferansen 2021 Kulometrija
Kulometrija Veterinaren fakultet skopje
Veterinaren fakultet skopje Fakultet za poslovni menadzment
Fakultet za poslovni menadzment Nacionalna olimpijada geografija
Nacionalna olimpijada geografija Fakultet u zrenjaninu
Fakultet u zrenjaninu Ekonomski fakultet zagreb smjerovi
Ekonomski fakultet zagreb smjerovi Poslovni menadzment bar
Poslovni menadzment bar Medicinski fakultet foca
Medicinski fakultet foca Foca medicinski fakultet
Foca medicinski fakultet Pravni fakultet univerziteta u travniku
Pravni fakultet univerziteta u travniku Pravni fakultet podgorica kontakt
Pravni fakultet podgorica kontakt Rimsko pravo katedra
Rimsko pravo katedra Ekonomski fakultet u banja luci
Ekonomski fakultet u banja luci Fakultet za poslovne studije
Fakultet za poslovne studije Ekonomski fakultet podgorica
Ekonomski fakultet podgorica Medicinski fakultet banja luka
Medicinski fakultet banja luka Fakultet za logistiku
Fakultet za logistiku Ups banja luka
Ups banja luka Unverstet
Unverstet Nezavisni fakultet banja luka
Nezavisni fakultet banja luka Slidetodoc
Slidetodoc Kineziologije
Kineziologije Domaci statistika poljoprivredni fakultet
Domaci statistika poljoprivredni fakultet Univerzitet u skoplju
Univerzitet u skoplju Istorija filozofski fakultet
Istorija filozofski fakultet Brodarski institut
Brodarski institut Dodatni bodovi za upis na fakultet djeca branitelja
Dodatni bodovi za upis na fakultet djeca branitelja Sociologija pravni fakultet
Sociologija pravni fakultet Bergen universitet psykologi
Bergen universitet psykologi Industrijski dizajn fakultet
Industrijski dizajn fakultet Singidunum poslovni fakultet
Singidunum poslovni fakultet Medicinski fakultet banja luka
Medicinski fakultet banja luka Poljoprivredni fakultet novi sad
Poljoprivredni fakultet novi sad