Nonlinear LeastSquares Regularized LeastSquares Why nonlinear The model

Non-linear Least-Squares Regularized Least-Squares

Why non-linear? • The model is non-linear (e. g. joints, position, . . ) • The error function is non-linear Regularized Least-Squares

Setup • Let f be a function such that where x is a vector of parameters Regularized Least-Squares

Setup • Let f be a function such that where x is a vector of parameters • Let {ak, bk} be a set of measurements/constraints. We fit f to the data by solving: Regularized Least-Squares

Setup • Let f be a function such that where x is a vector of parameters • Let {ak, bk} be a set of measurements/constraints. We fit f to the data by solving: Regularized Least-Squares

Example Regularized Least-Squares

Overview • • • Existence and uniqueness of minimum Steepest-descent Newton’s method Gauss-Newton’s method Levenberg-Marquardt method Regularized Least-Squares

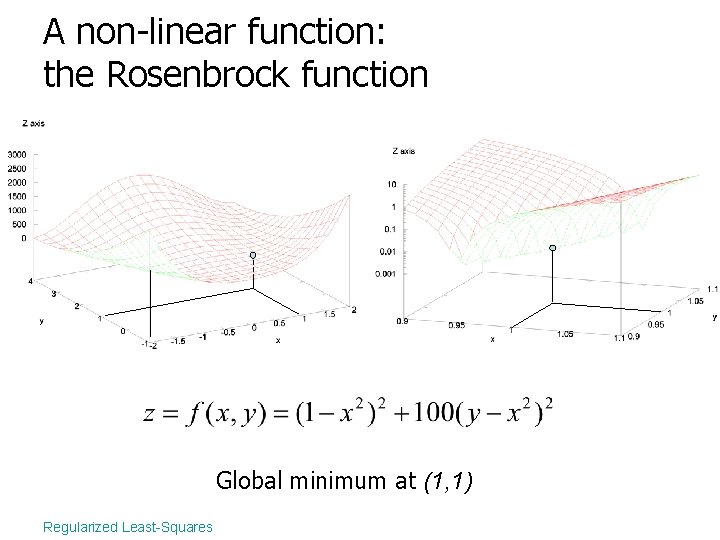
A non-linear function: the Rosenbrock function Global minimum at (1, 1) Regularized Least-Squares

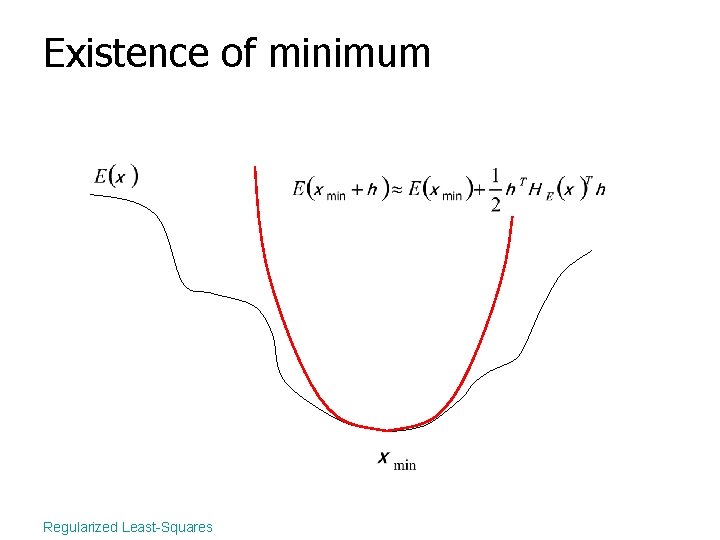
Existence of minimum A local minima is characterized by: 1. 2. Regularized Least-Squares

Existence of minimum Regularized Least-Squares

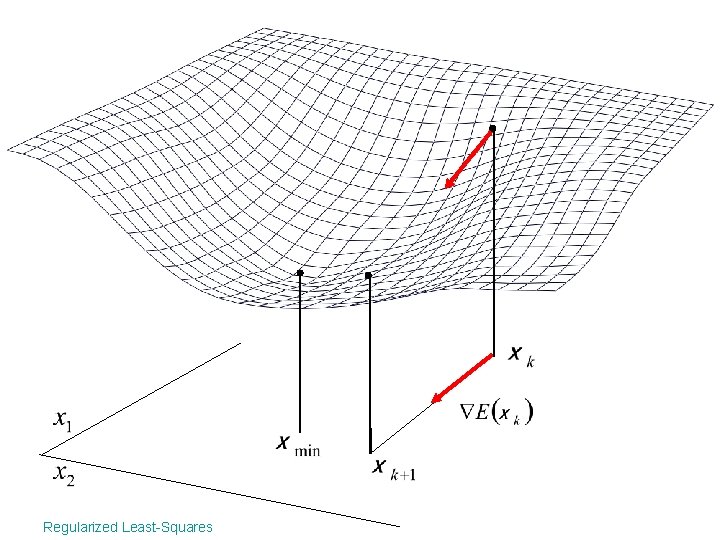
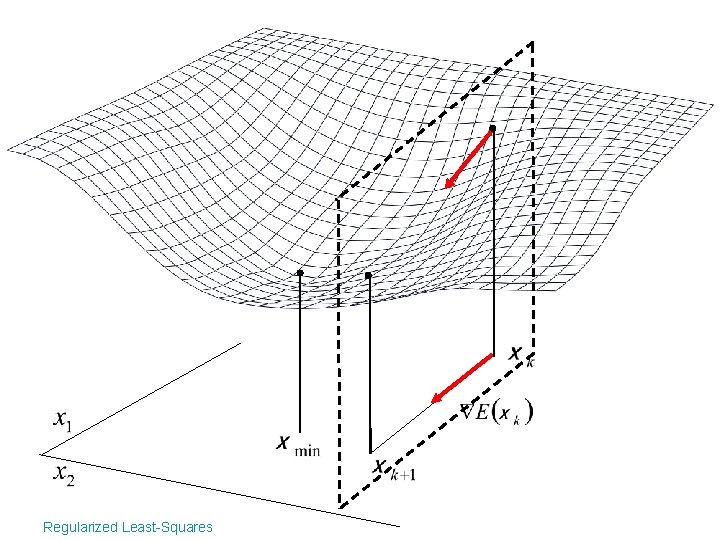
Descent algorithm • Start at an initial position x 0 • Until convergence – Find minimizing step dxk – xk+1=xk+ dxk Produce a sequence x 0, x 1, …, xn such that f(x 0) > f(x 1) > …> f(xn) Regularized Least-Squares

Descent algorithm • Start at an initial position x 0 • Until convergence – Find minimizing step dxk using a local approximation of f – xk+1=xk+ dxk Produce a sequence x 0, x 1, …, xn such that f(x 0) > f(x 1) > …> f(xn) Regularized Least-Squares

Approximation using Taylor series Regularized Least-Squares

Approximation using Taylor series Regularized Least-Squares

Approximation using Taylor series Regularized Least-Squares

Steepest descent Step where is chosen such that: using a line search algorithm: Regularized Least-Squares

Regularized Least-Squares

Regularized Least-Squares

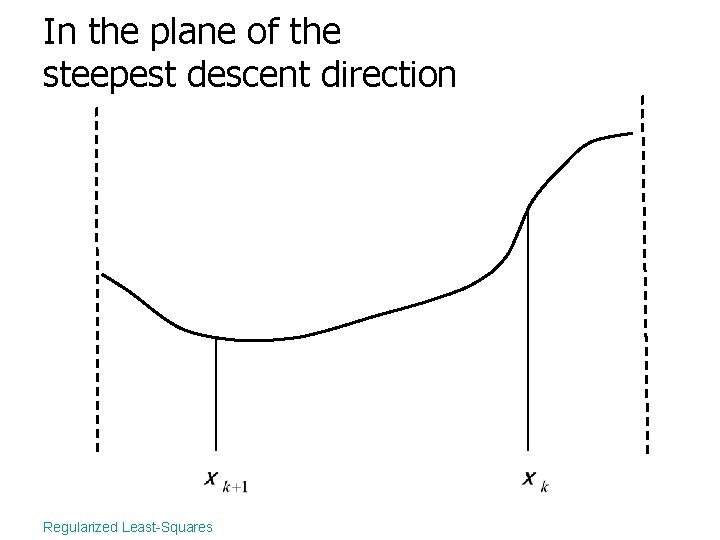
In the plane of the steepest descent direction Regularized Least-Squares

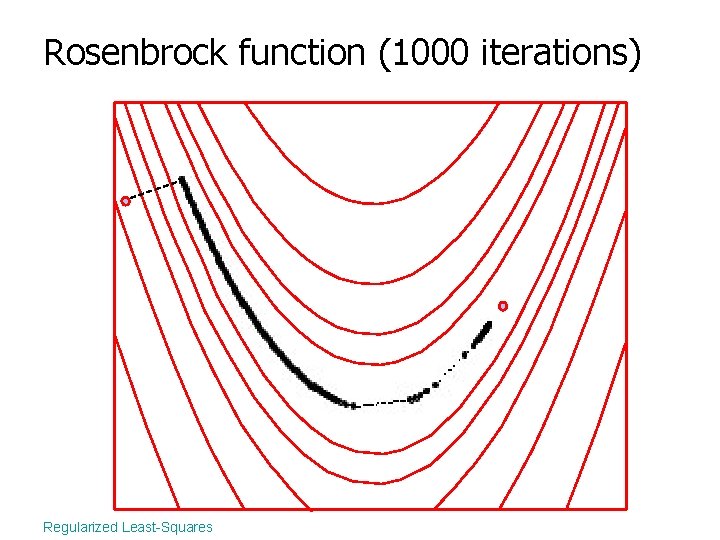
Rosenbrock function (1000 iterations) Regularized Least-Squares

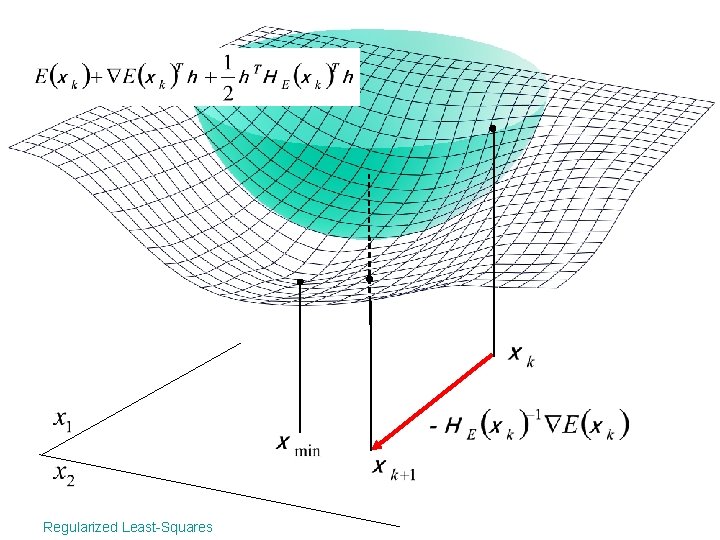
Newton’s method • Step: second order approximation At the minimum of N Regularized Least-Squares

Regularized Least-Squares

Problem • If is not positive semi-definite, then is not a descent direction: the step increases the error function • Uses positive semi-definite approximation of Hessian based on the jacobian (quasi-Newton methods) Regularized Least-Squares

Gauss-Newton method Step: use with the approximate hessian Advantages: • No second order derivatives • is positive semi-definite Regularized Least-Squares

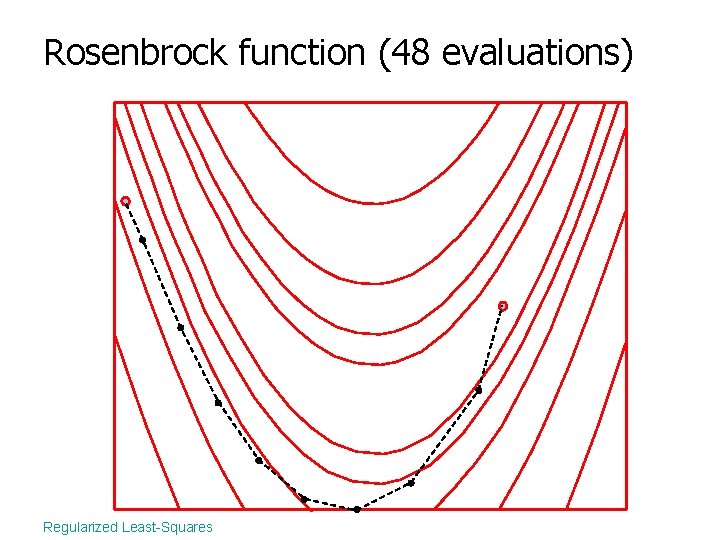
Rosenbrock function (48 evaluations) Regularized Least-Squares

Levenberg-Marquardt algorithm • Blends Steepest descent and Gauss-Newton • At each step solve, for the descent direction Regularized Least-Squares

Managing the damping parameter • General approach: – If step fails, increase damping until step is successful – If step succeeds, decrease damping to take larger step • Improved damping Regularized Least-Squares

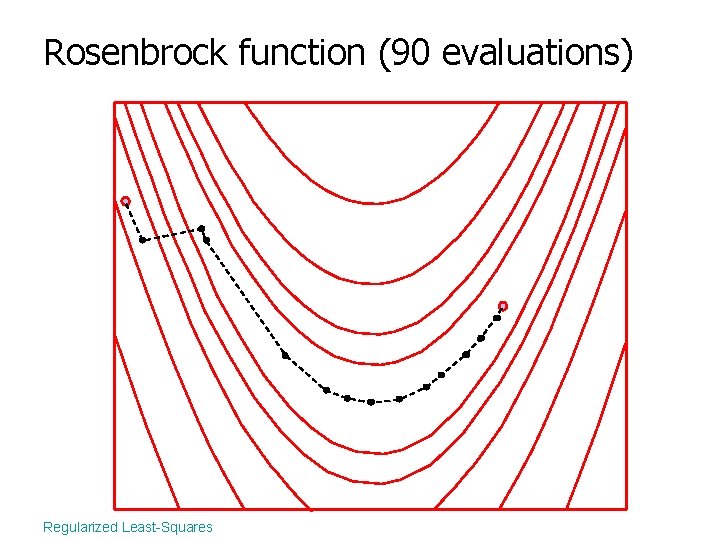
Rosenbrock function (90 evaluations) Regularized Least-Squares

“Resynthesizing Facial Animation through 3 D Model-Based Tracking”, Pighin etal. , + + Video frame Regularized Least-Squares Model

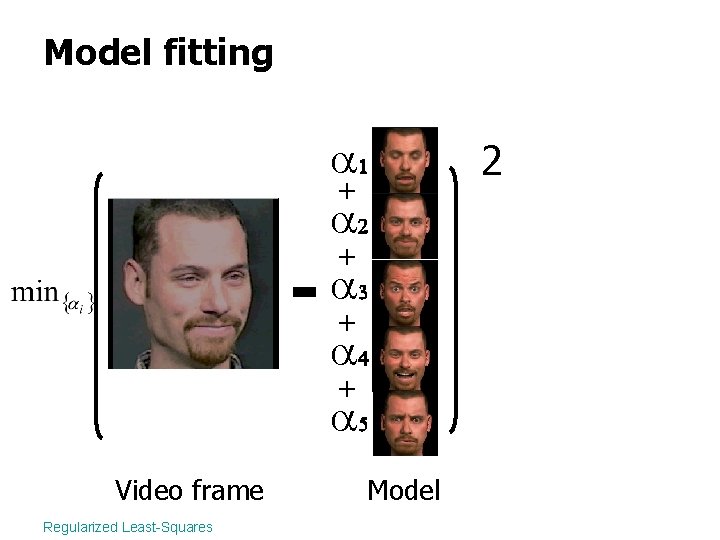
Model fitting + Video frame Regularized Least-Squares + + + Model 2

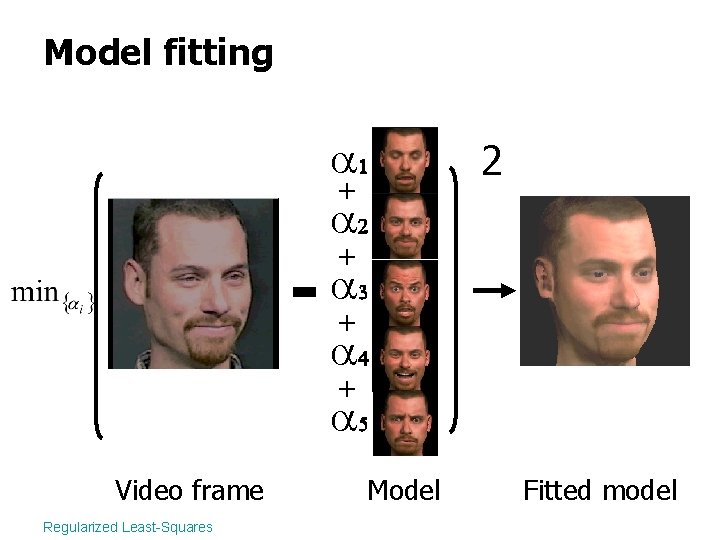
Model fitting + Video frame Regularized Least-Squares 2 + + + Model Fitted model

“Resynthesizing Facial Animation through 3 D Model -Based Tracking”, Pighin etal. , • Facial tracking by fitting face model Regularized Least-Squares

“Resynthesizing Facial Animation through 3 D Model -Based Tracking”, Pighin etal. , • Facial tracking by fitting face model • Problem – Given an image I – A 3 D face model Regularized Least-Squares

“Resynthesizing Facial Animation through 3 D Model -Based Tracking”, Pighin etal. , • Facial tracking by fitting face model • Problem – Given an image I – A 3 D face model Minimize Where And is the image produced by the face model is a regularization term. Regularized Least-Squares

Problem setup Regularized Least-Squares

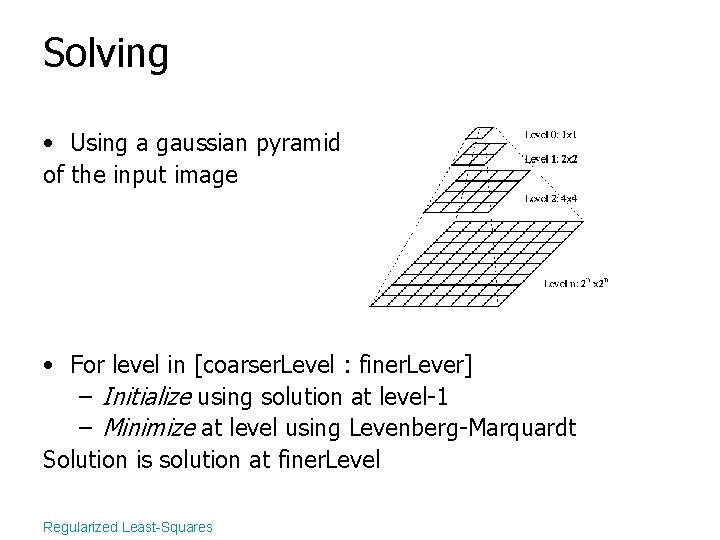
Solving • Using a gaussian pyramid of the input image • For level in [coarser. Level : finer. Lever] – Initialize using solution at level-1 – Minimize at level using Levenberg-Marquardt Solution is solution at finer. Level Regularized Least-Squares

Tracking results Regularized Least-Squares

Conclusion • Get a good initial guess Prediction (temporal/spatial coherency) Partial solve Prior knowledge • Levenberg-Marquardt is your friend Regularized Least-Squares