Lattice regularized diffusion Monte Carlo Michele Casula Claudia

Lattice regularized diffusion Monte Carlo Michele Casula, Claudia Filippi, Sandro Sorella International School for Advanced Studies, Trieste, Italy National Center for Research in Atomistic Simulation

Outline q. Review of Diffusion Monte Carlo and Motivations q. Review of Lattice Green function Monte Carlo q Lattice regularized Hamiltonian q Applications q Conlcusions

Standard DMC stochastic method to solve H with boundary conditions given by the nodes of (fixed node approximation) DIFFUSION WITH DRIFT BRANCHING Imaginary time Schroedinger equation with importance sampling MIXED AVERAGE ESTIMATE computed by DMC “PURE” EXPECTATION VALUE if

Motivations Major drawbacks of the standard Diffusion Monte Carlo • bad scaling of DMC with the atomic number D. M. Ceperley, J. Stat. Phys. 43, 815(1986) A. Ma et al. , to appear in PRA • locality approximation needed in the presence of non local potentials (pseudopotentials) non variational results simulations less stable when pseudo are included great dependence on the guidance wave function used however approximation is exact if guidance is exact

Non local potentials Locality approximation in DMC Mitas et al. J. Chem. Phys. 95, 3467 (1991) Effective Hamiltonian HLA containing the localized potential: • the mixed estimate is not variational since • if is exact, the approximation is exact (in general it will depend on the shape of )

Pseudopotentials q For heavy atoms pseudopotentials are necessary to reduce the computational time q Usually they are non local In QMC angular momentum projection is calculated by using a quadrature rule for the integration S. Fahy, X. W. Wang and Steven G. Louie, PRB 42, 3503 (1990) Natural discretization of the projection Can a lattice scheme be applied?

Lattice GFMC Lattice hamiltonian: Propagator: Hopping: importance sampling transition probability weight For fermions, lattice fixed node approx to have a well defined transition probability

Effective Hamiltonian Hop with sign change replaced by a positive diagonal potential LATTICE UPPER BOUND THEOREM ! D. F. B. ten Haaf et al. PRB 51, 13039 (1995)

Lattice regularization I Kinetic term: discretization of the laplacian One dimension: General case: where hopping term t 1/a 2

Lattice regularization II Double mesh for the discretized laplacian Separation of core and valence dynamics for heavy nuclei two hopping terms in the kinetic part p can depend on the distance from the nucleus Our choice: Moreover, if b is not a multiple of a, the random walk can sample all the space!

Lattice regularized H Definition of lattice regularized Hamiltonian Ø Continuous limit: for a 0, Ha H Ø Local energy of Ha = local energy of H Ø Discretized kinetic energy = continuous kinetic energy Faster convergence in a!

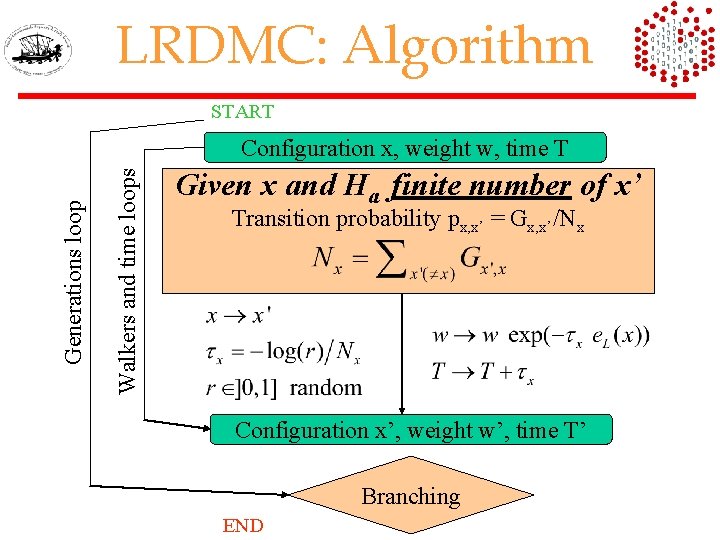
LRDMC: Algorithm START Walkers and time loops Generations loop Configuration x, weight w, time T Given x and Ha finite number of x’ Transition probability px, x’ = Gx, x’/Nx Configuration x’, weight w’, time T’ Branching END

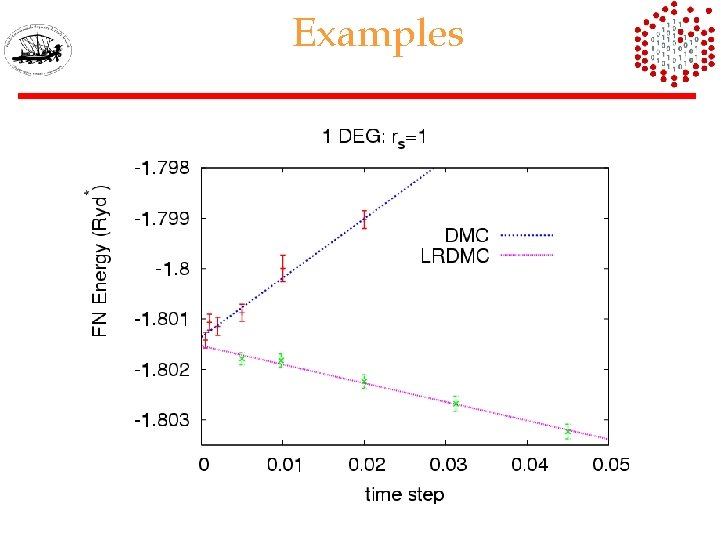
DMC vs LRDMC extrapolation properties same diffusion constant CPU time with two different meshes gain in decorrelation

Examples Carbon atom

LRDMC with pseudo I Off diagonal matrix elements From the discretized Laplacian a and b: translation vectors From the non local pseudopotential c quadrature mesh (rotation around a nucleus)

LRDMC with pseudo II Effective lattice regularized Hamiltonian Now kinetic & pseudo! • Mixed average is variational • Pure expectation value of H can be estimated • Much more stable than the locality approximation (less statistical fluctuations)

Pure energy estimate Hellmann-Feynman theorem Different ways to estimate the derivative: § Finite differences § Correlated sampling Variational due to the convexity of Exact for reachable only with correlated sampling (without losing efficiency)

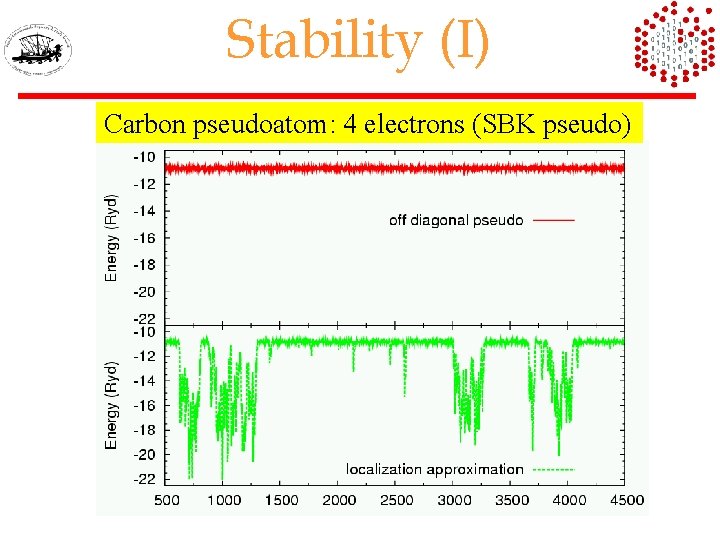
Stability (I) Carbon pseudoatom: 4 electrons (SBK pseudo)

Stability (II) Nodal surface non local move q locality approximation infinitely negative attractive potential close to the nodal surface (It works for good trial functions / small time steps) q non local move escape from nodes

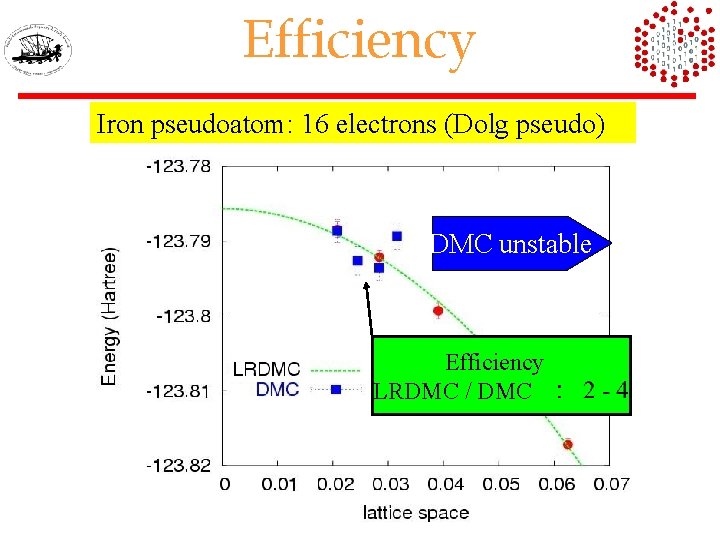
Efficiency Iron pseudoatom: 16 electrons (Dolg pseudo) DMC unstable Efficiency LRDMC / DMC

LRDMC and locality More general effective Hamiltonian off diagonal pseudo (with FN approximation) locality approximation + FN approximation interpolates between two regimes: we can check the quality of the FN state given by the locality approx.

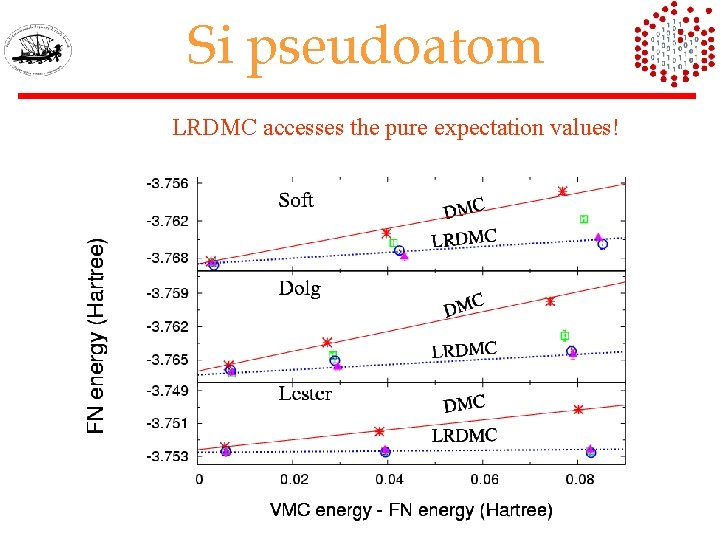
Si pseudoatom LRDMC accesses the pure expectation values!

Scandium 4 s 23 dn 4 s 13 dn+1 excitation energies e. V VMC DMC LRDMC 2 body 1. 099(30) 1. 381(15) 1. 441(25) 3 body 1. 303(29) 1. 436(22) 1. 478(22) Experimental value: 1. 43 e. V LRDMC: two simulations with for and

Iron dimer Ground state LRDMC (Dolg pseudo) gives: MRCI Chemical Physics Letter, 358 (2002) 442 DFT-PP 86 Physical Review B, 66 (2002) 155425

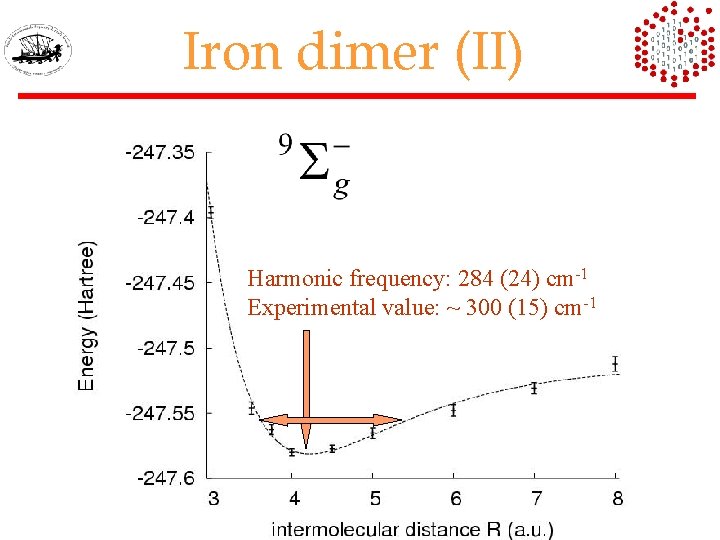
Iron dimer (II) -1 Harmonicequilibrium LRDMC frequency: distance: 284 (24) cm 4. 22(5) Experimental value: ~ 300 3. 8 (15) cm-1

Conclusions ü LRDMC as an alternative variational approach for dealing with non local potentials ü Pure energy expectation values accessible ü The FN energy depends only on the nodes and very weakly on the amplitudes of ü Very stable simulation also for poor wave functions ü Double mesh more efficient for “heavy” nuclei Reference: cond-mat/0502388

Limit L On the continuous, usually H not bounded from above! Green function expansion Probability of leaving x Probabilty of leaving x after k time slices k distributed accordingly to f