Regularized LeastSquares Outline Why regularization Truncated Singular Value

Regularized Least-Squares

Outline • • Why regularization? Truncated Singular Value Decomposition Damped least-squares Quadratic constraints Regularized Least-Squares

Why regularization? • We have seen that Regularized Least-Squares

Why regularization? • We have seen that • But what happens if the system is almost dependent? – The solution becomes very sensitive to the data – Poor conditioning Regularized Least-Squares

The 1 -dimensional case • The 1 -dimensional normal equation Regularized Least-Squares

The 1 -dimensional case • The 1 -dimensional normal equation Regularized Least-Squares

The 1 -dimensional case • The 1 -dimensional normal equation Regularized Least-Squares

Why regularization • Contradiction between data and model Regularized Least-Squares

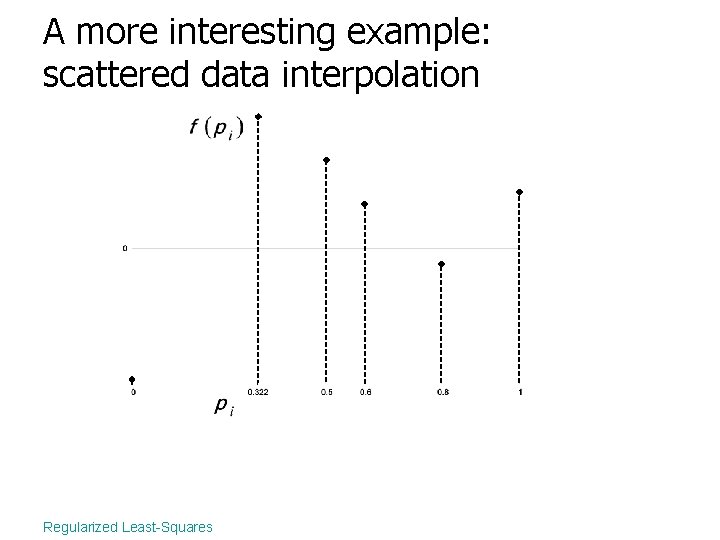
A more interesting example: scattered data interpolation Regularized Least-Squares

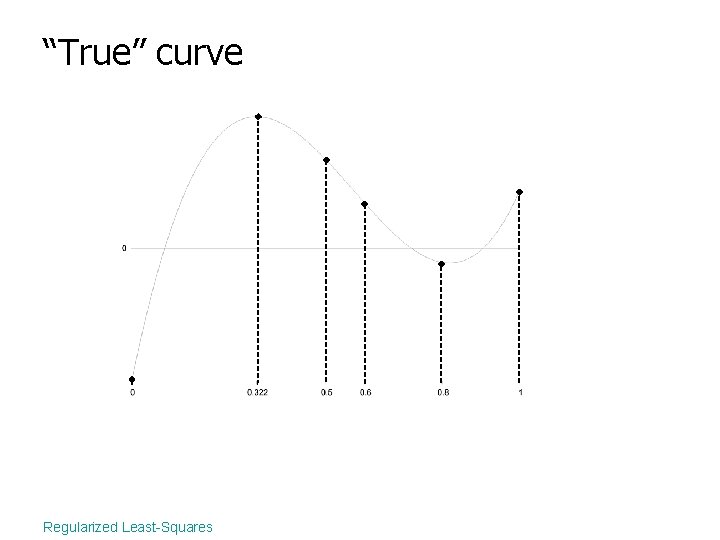
“True” curve Regularized Least-Squares

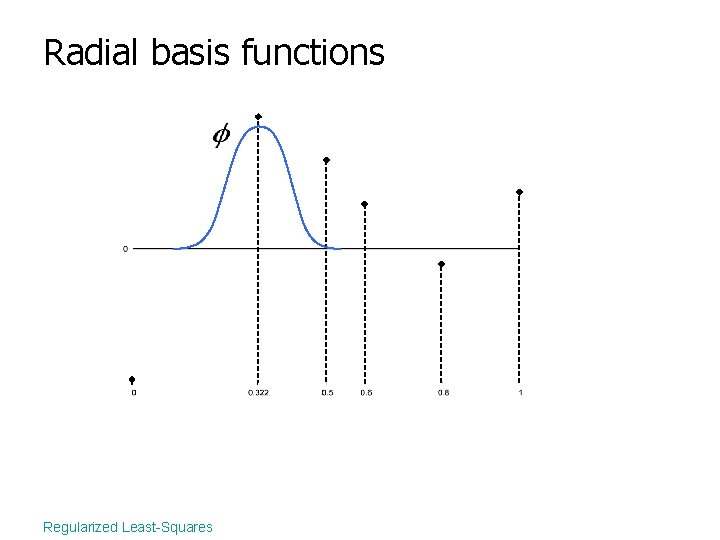
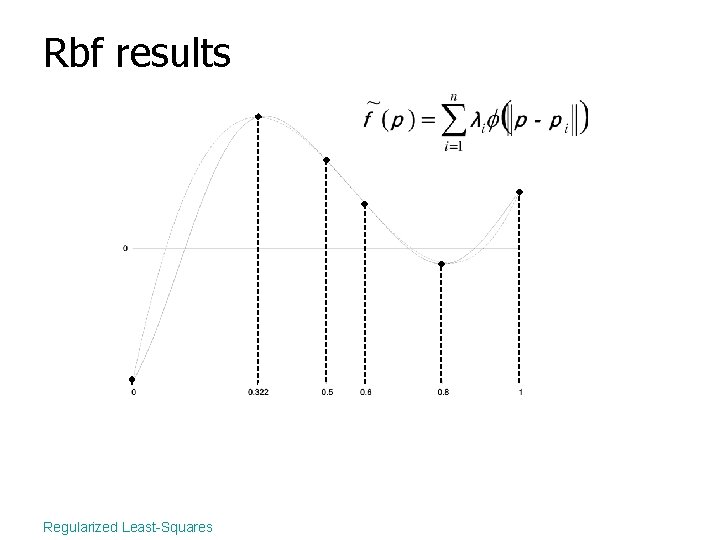
Radial basis functions Regularized Least-Squares

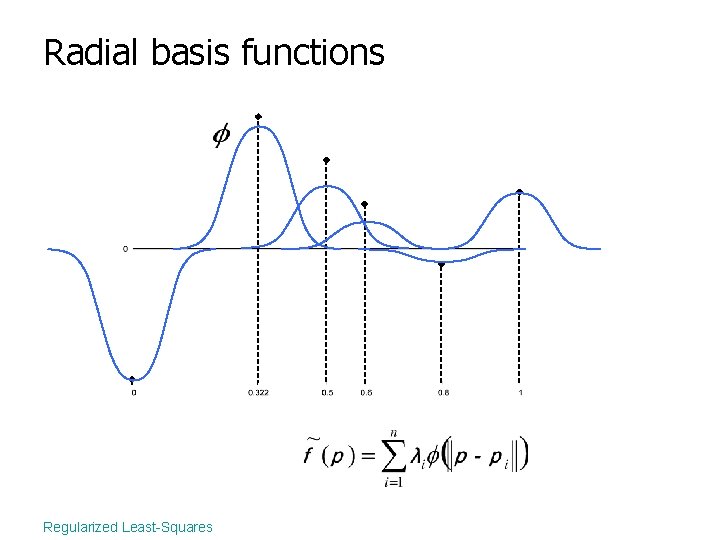
Radial basis functions Regularized Least-Squares

Rbf are popular • Modeling – – J. C. Carr, R. K. Beatson, J. B. Cherrie, T. J. Mitchell, W. R. Fright, B. C. Mc. Callum, and T. R. Evans. Reconstruction and representation of 3 d objects with radial basis functions. In Proceedings of ACM SIGGRAPH 2001, Computer Graphics Proceedings, Annual Conference Series, pages 67– 76, August 2001. G. Turk and J. F. O’Brien. Modelling with implicit surfaces that interpolate. ACM Transactions on Graphics, 21(4): 855– 873, October 2002. • Animation – – J. Noh and U. Neumann. Expression cloning. In Proceedings of ACMSIGGRAPH 2001, Computer Graphics Proceedings, Annual Conference Series, pages 277– 288, August 2001. F. Pighin, J. Hecker, D. Lischinski, R. Szeliski, and D. H. Salesin. Synthesizing realistic facial expressions from photographs. In Proceedings of SIGGRAPH 98, Computer Graphics Proceedings, Annual Conference Series, pages 75– 84, July 1998. Regularized Least-Squares

Radial basis functions • At every point Regularized Least-Squares

Radial basis functions • At every point • Solve the least-squares problem Regularized Least-Squares

Radial basis functions • At every point • Solve the least-squares problem Regularized Least-Squares

Rbf results Regularized Least-Squares

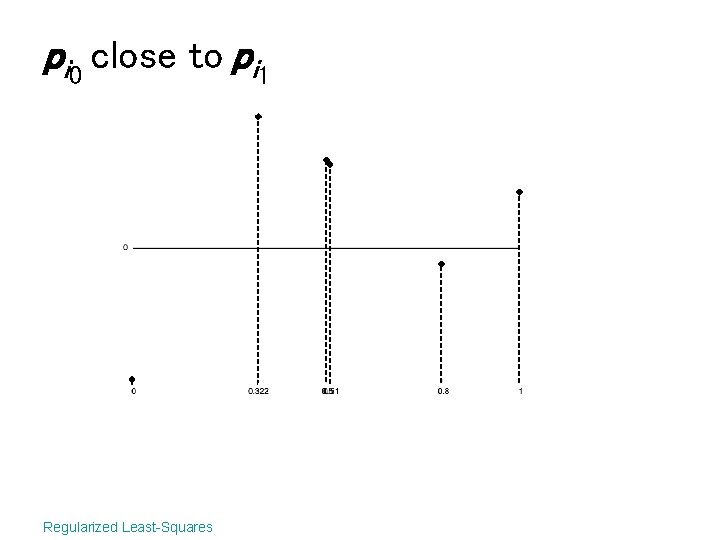
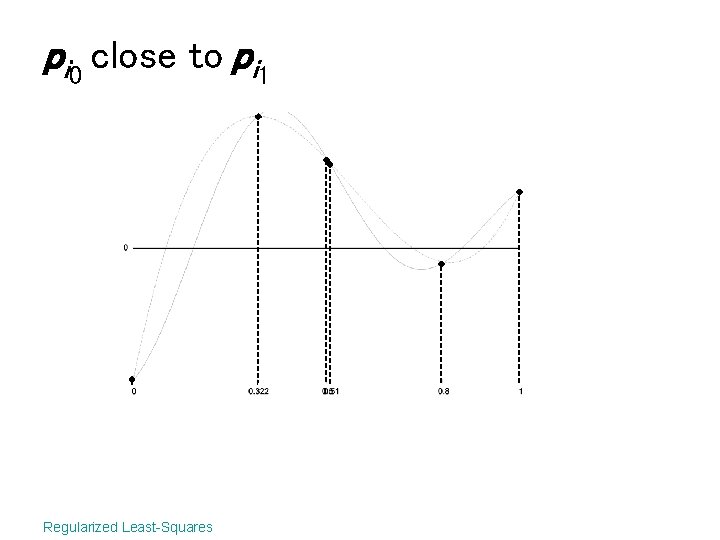
pi 0 close to pi 1 Regularized Least-Squares

Radial basis functions • At every point • Solve the least-squares problem Regularized Least-Squares

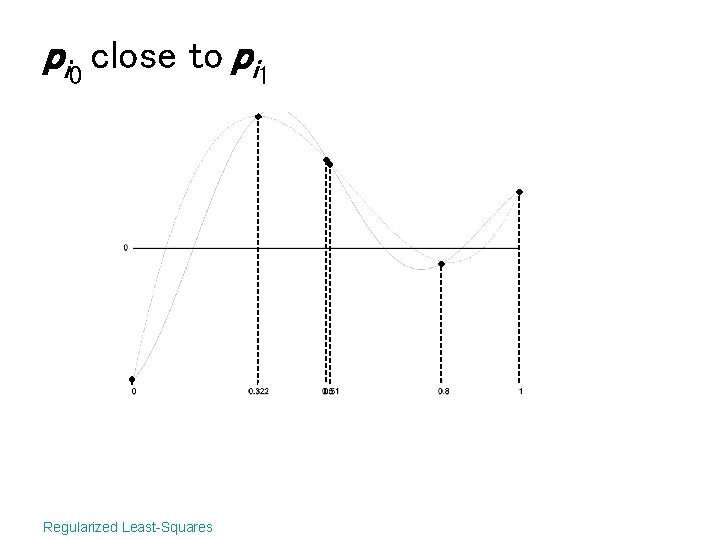
Radial basis functions • At every point • Solve the least-squares problem • If pi 0 close to pi 1, A is near singular Regularized Least-Squares

pi 0 close to pi 1 Regularized Least-Squares

pi 0 close to pi 1 Regularized Least-Squares

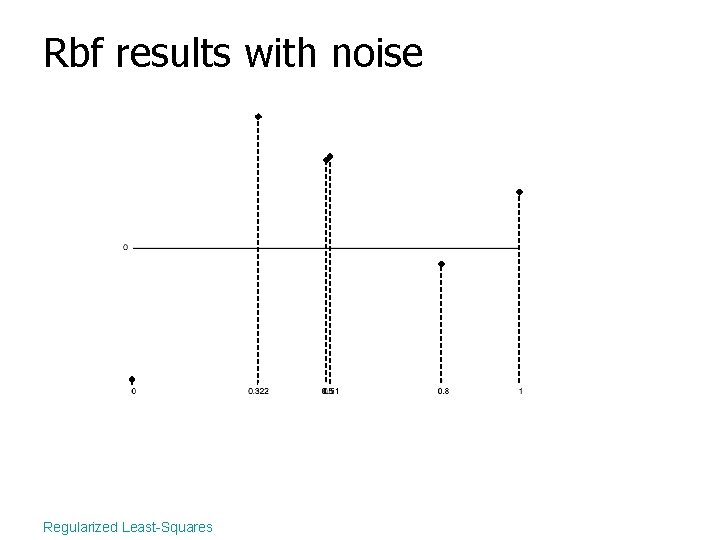
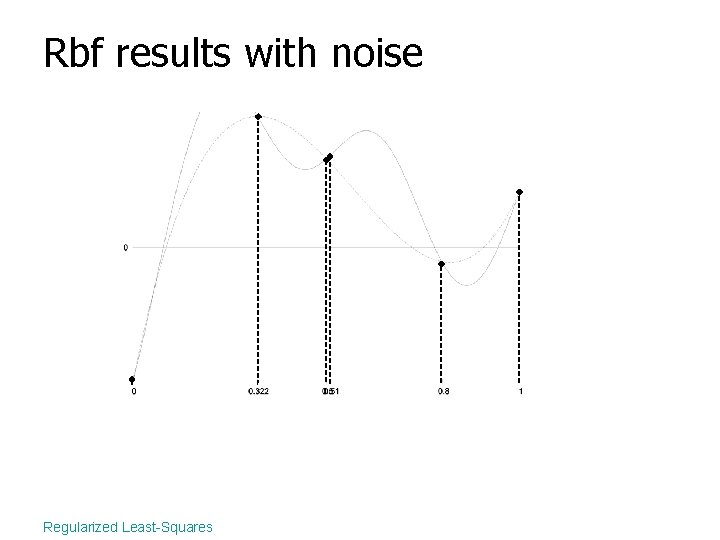
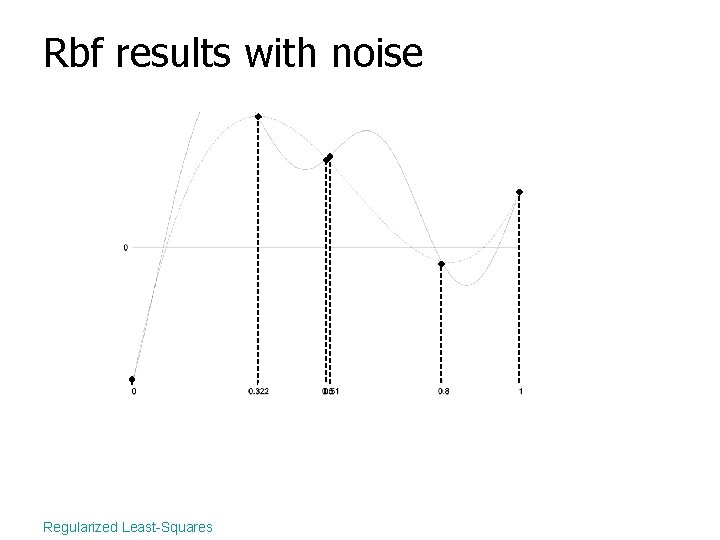
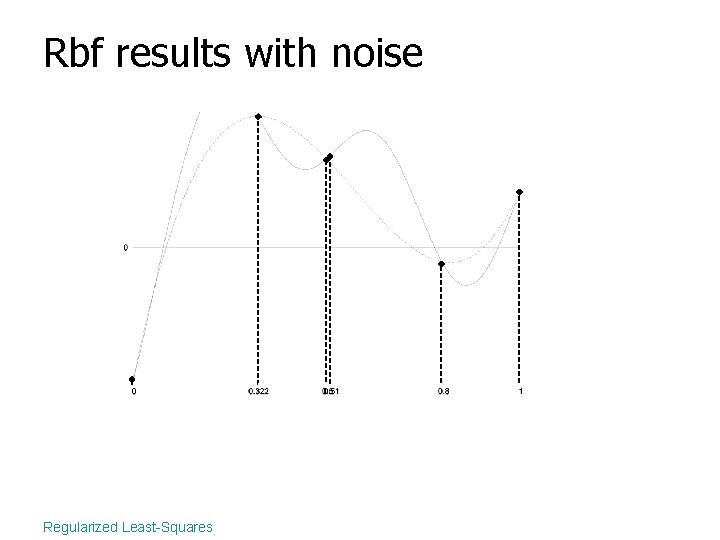
Rbf results with noise Regularized Least-Squares

Rbf results with noise Regularized Least-Squares

The Singular Value Decomposition • Every matrix A (nxm) can be decomposed into: – where • U is an nxn orthogonal matrix • V is an mxm orthogonal matrix • D is an nxm diagonal matrix Regularized Least-Squares

The Singular Value Decomposition • Every matrix A (nxm) can be decomposed into: – where • U is an nxn orthogonal matrix • V is an mxm orthogonal matrix • D is an nxm diagonal matrix Regularized Least-Squares

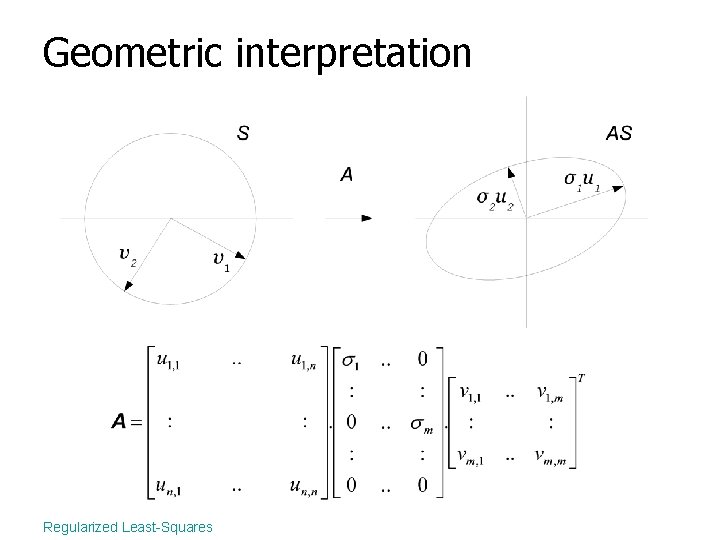
Geometric interpretation Regularized Least-Squares

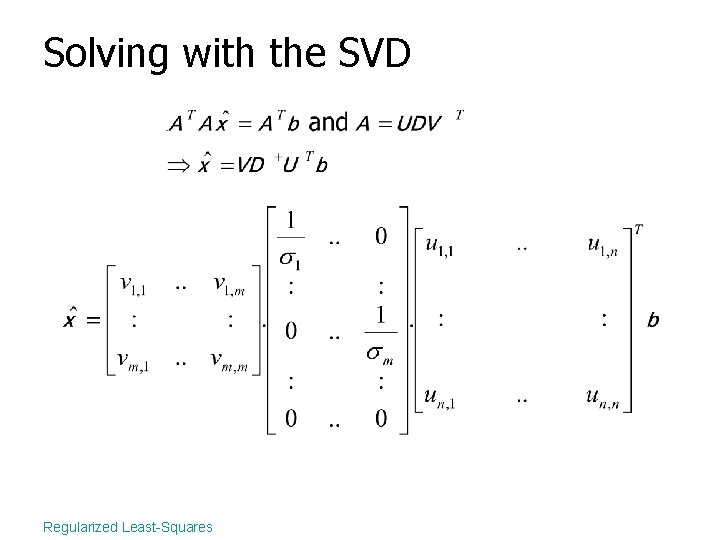
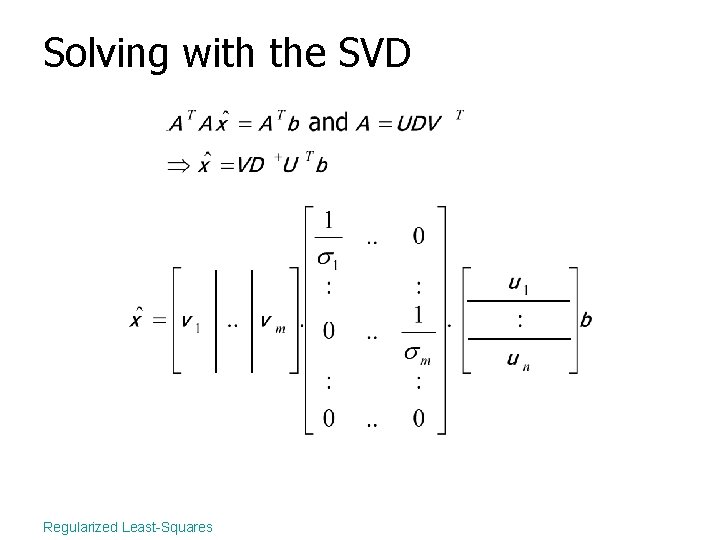
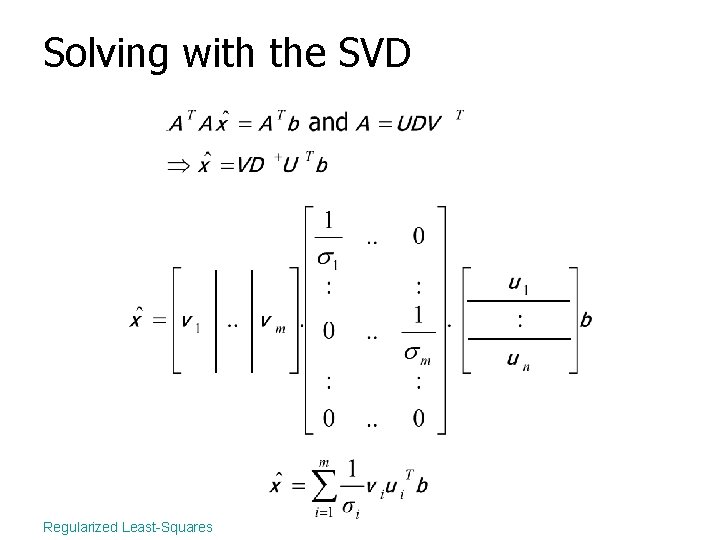
Solving with the SVD Regularized Least-Squares

Solving with the SVD Regularized Least-Squares

Solving with the SVD Regularized Least-Squares

Solving with the SVD Regularized Least-Squares

Solving with the SVD Regularized Least-Squares

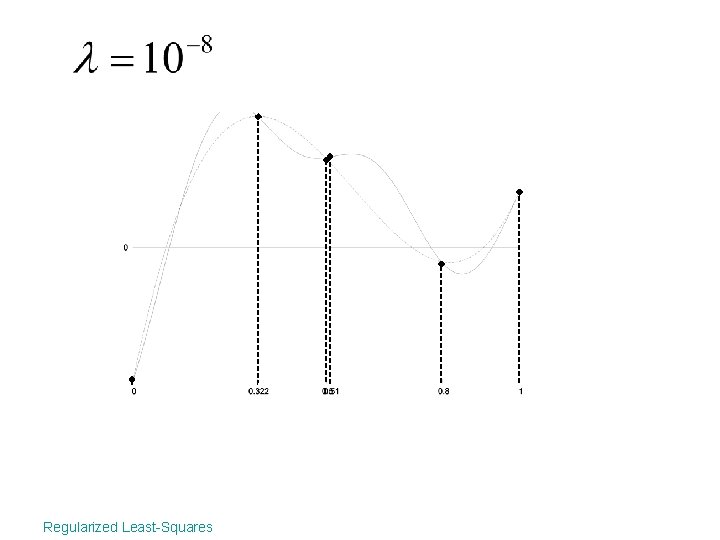
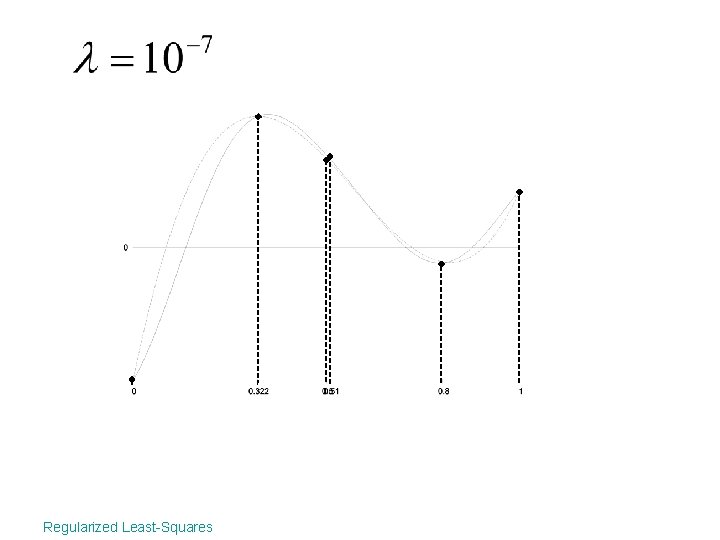
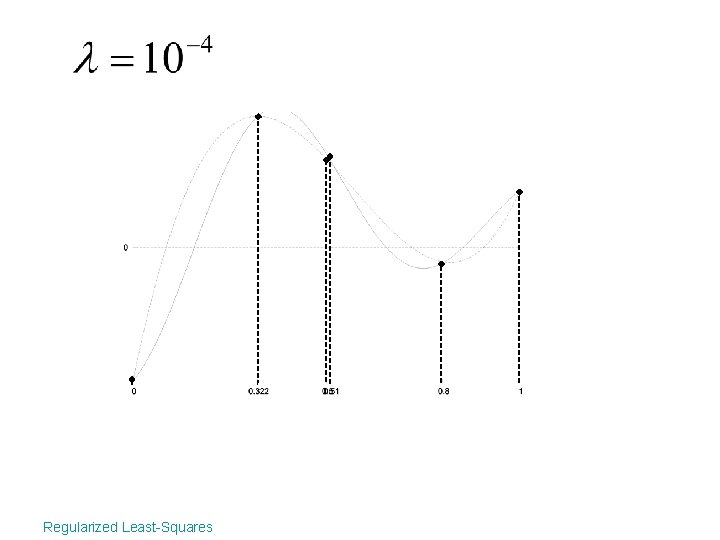
A is nearly rank defficient Regularized Least-Squares

A is nearly rank defficient Regularized Least-Squares

A is nearly rank defficient Regularized Least-Squares

A is nearly rank defficient • A is nearly rank defficient =>some of the are close to 0 Regularized Least-Squares

A is nearly rank defficient • A is nearly rank defficient =>some of the are close to 0 =>some of the are close to Regularized Least-Squares

A is nearly rank defficient • A is nearly rank defficient =>some of the are close to 0 =>some of the are close to • Problem with Regularized Least-Squares

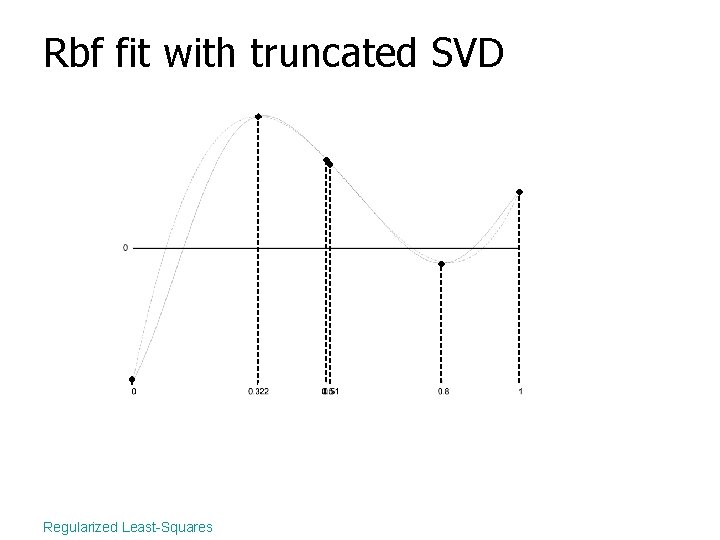
A is nearly rank defficient • A is nearly rank defficient =>some of the are close to 0 =>some of the are close to • Problem with • Truncate the SVD Regularized Least-Squares

pi 0 close to pi 1 Regularized Least-Squares

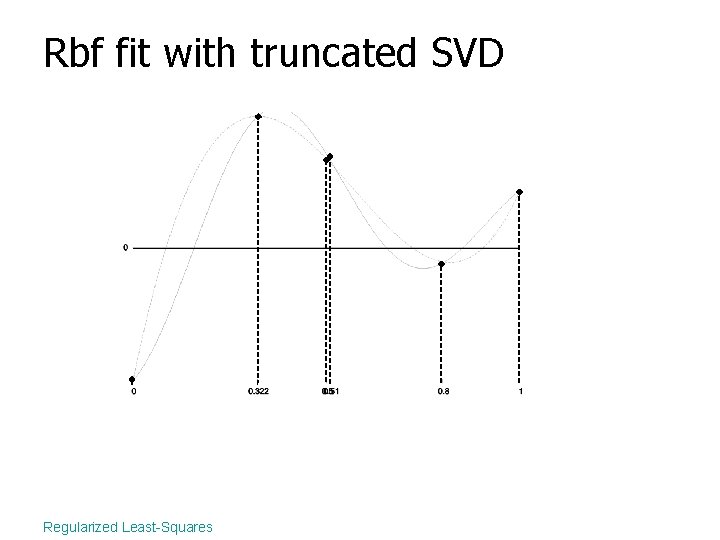
Rbf fit with truncated SVD Regularized Least-Squares

Rbf results with noise Regularized Least-Squares

Rbf fit with truncated SVD Regularized Least-Squares

Choosing cutoff value k • The first k such as Regularized Least-Squares

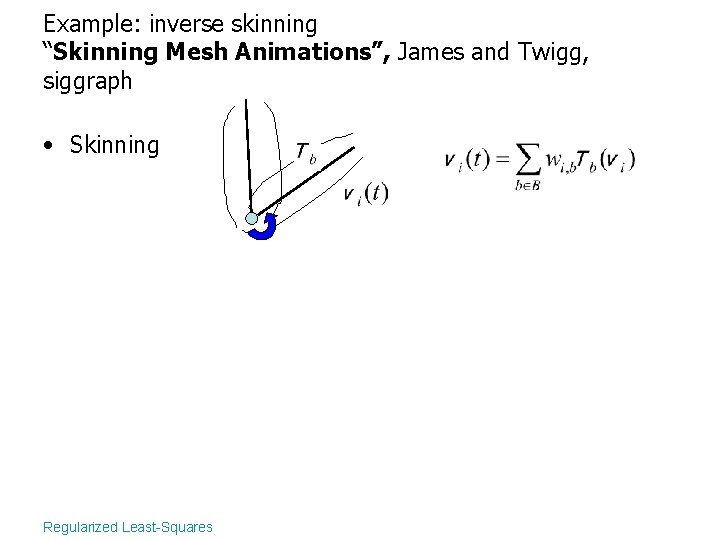
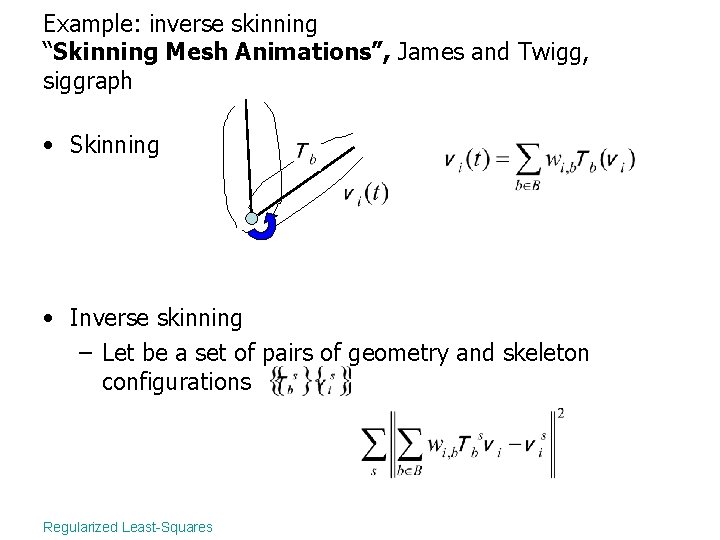
Example: inverse skinning “Skinning Mesh Animations”, James and Twigg, siggraph • Skinning Regularized Least-Squares

Example: inverse skinning “Skinning Mesh Animations”, James and Twigg, siggraph • Skinning ? Regularized Least-Squares

Example: inverse skinning “Skinning Mesh Animations”, James and Twigg, siggraph • Skinning Regularized Least-Squares

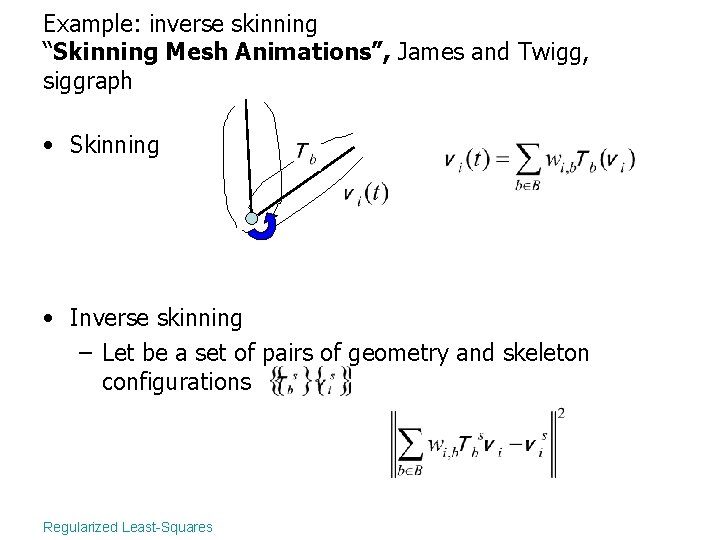
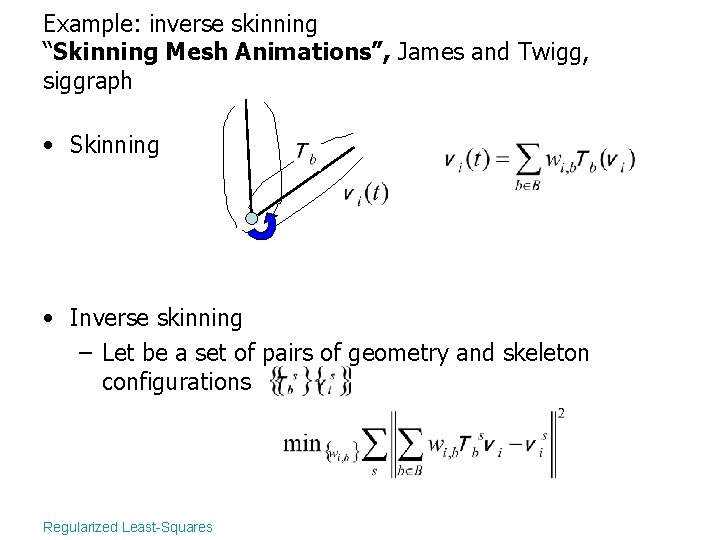
Example: inverse skinning “Skinning Mesh Animations”, James and Twigg, siggraph • Skinning • Inverse skinning – Let be a set of pairs of geometry and skeleton configurations Regularized Least-Squares

Example: inverse skinning “Skinning Mesh Animations”, James and Twigg, siggraph • Skinning • Inverse skinning – Let be a set of pairs of geometry and skeleton configurations Regularized Least-Squares

Example: inverse skinning “Skinning Mesh Animations”, James and Twigg, siggraph • Skinning • Inverse skinning – Let be a set of pairs of geometry and skeleton configurations Regularized Least-Squares

Example: inverse skinning “Skinning Mesh Animations”, James and Twigg, siggraph • Skinning • Inverse skinning – Let be a set of pairs of geometry and skeleton configurations Regularized Least-Squares

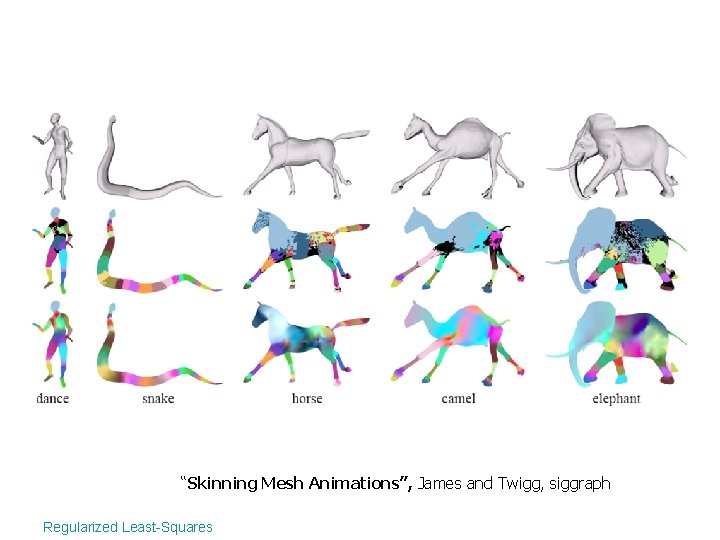
“Skinning Mesh Animations”, James and Twigg, siggraph Regularized Least-Squares

Problem with the TSVD • We have to compute the SVD of A, and O() process: impractical for large marices • Little control over regularization Regularized Least-Squares

Damped least-squares • Replace by where is a scalar and L is a matrix Regularized Least-Squares

Damped least-squares • Replace by where is a scalar and L is a matrix The solution verifies Regularized Least-Squares

Examples of L Diagonal Limit scale Regularized Least-Squares Differential Enforce smoothness

Rbf results with noise Regularized Least-Squares

Regularized Least-Squares

Regularized Least-Squares

Regularized Least-Squares

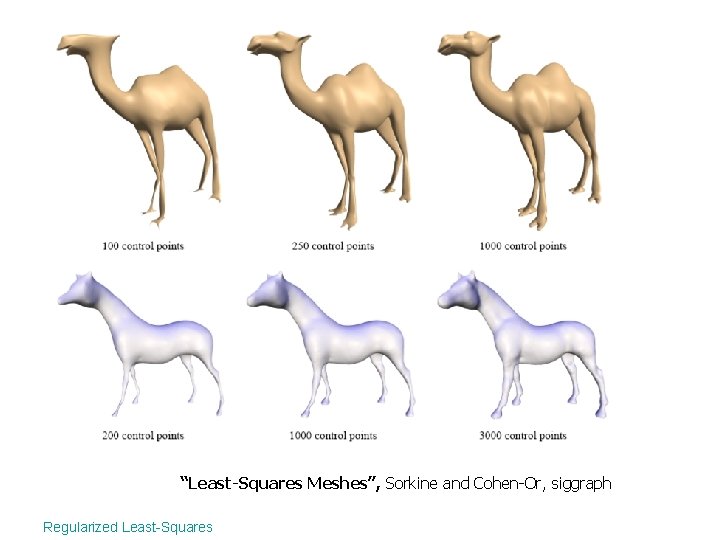
Example: “Least-Squares Meshes”, Sorkin and Cohen-Or, siggaph • Reconstruct a mesh given – Control points – Connectivity (planar mesh) Regularized Least-Squares

Example: “Least-Squares Meshes”, Sorkin and Cohen-Or, siggaph • Reconstruct a mesh given – Control points – Connectivity (planar mesh) • Smooth reconstruction Regularized Least-Squares

Example: “Least-Squares Meshes”, Sorkin and Cohen-Or, siggaph • Reconstruct a mesh given – Control points – Connectivity (planar mesh) • Smooth reconstruction • In matrix form Regularized Least-Squares

Reconstruction • Minimize reconstruction error where Regularized Least-Squares

“Least-Squares Meshes”, Sorkine and Cohen-Or, siggraph Regularized Least-Squares

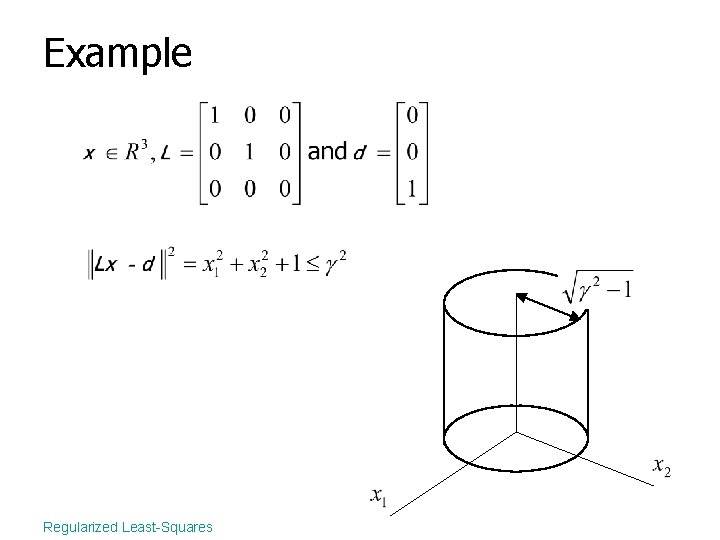
Quadratic constraints • Solve or Regularized Least-Squares

Quadratic constraints • Solve or Regularized Least-Squares

Example Regularized Least-Squares

Example Regularized Least-Squares

Example Regularized Least-Squares

Discussion • If no x for which Regularized Least-Squares , there is no solution (since there is )

Discussion • If no x for which , there is no solution (since there is ) • If , the solution exists and is unique Regularized Least-Squares

Discussion • If no x for which , there is no solution (since there is ) • If , the solution exists and is unique – Either the solution of feasible set Regularized Least-Squares is in the

Discussion • If no x for which , there is no solution (since there is ) • If , the solution exists and is unique – Either the solution of feasible set – or the solution is at the boundary Solve Regularized Least-Squares is in the

Discussion Solve where is a Lagrange multiplier Regularized Least-Squares

Conclusion • TSVD really useful if you need an SVD Regularized Least-Squares

Conclusion • TSVD really useful if you need an SVD • Regularization constrains the solution: – Value, differential operator, other properties – Soft (damping) or hard constraint (quadratic) – Linear or non-linear Regularized Least-Squares

Conclusion • TSVD really useful if you need an SVD • Regularization constrains the solution: – Value, differential operator, other properties – Soft (damping) or hard constraint (quadratic) – Linear or non-linear • Danger of over-damping or constraining Regularized Least-Squares

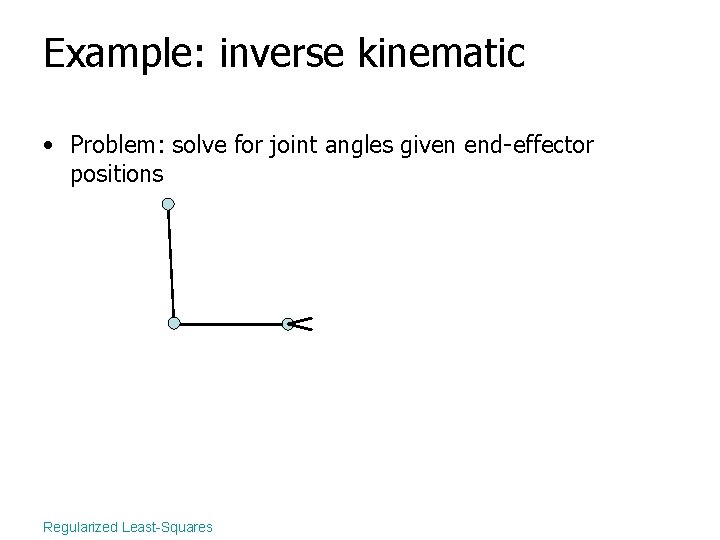
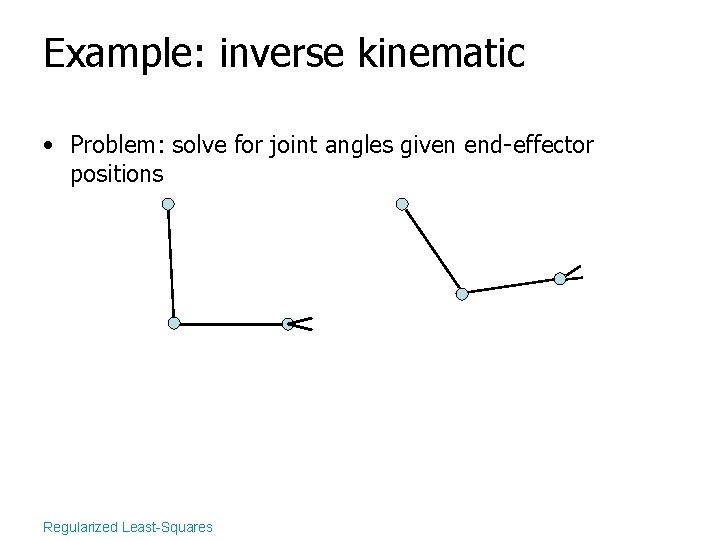
Example: inverse kinematic • Problem: solve for joint angles given end-effector positions Regularized Least-Squares

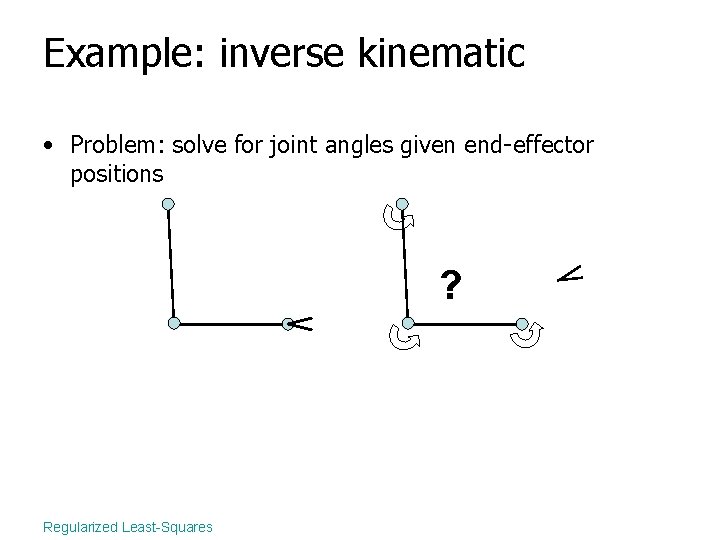
Example: inverse kinematic • Problem: solve for joint angles given end-effector positions ? Regularized Least-Squares

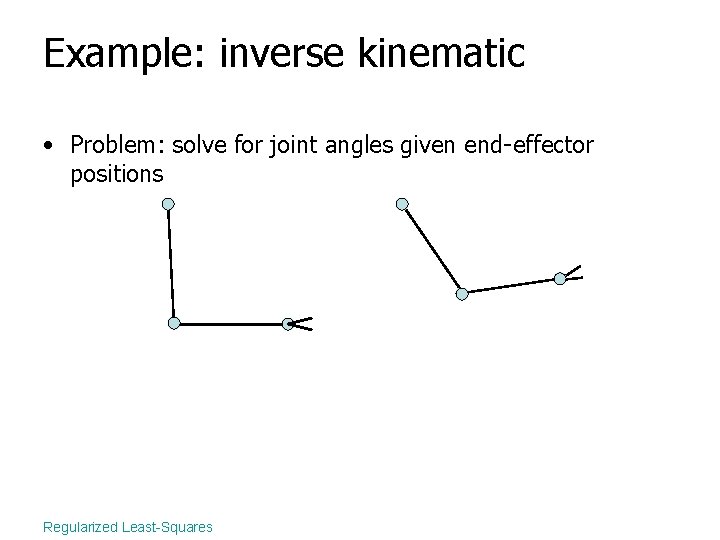
Example: inverse kinematic • Problem: solve for joint angles given end-effector positions Regularized Least-Squares

Example: inverse kinematic • Problem: solve for joint angles given end-effector positions Regularized Least-Squares