Calculate Present or Future Value of Cash Flows































- Slides: 50

Calculate Present or Future Value of Cash Flows Principles of Cost Analysis and Management © Dale R. Geiger 2011 1

Time Value of Money Concepts • Is $1 received today worth the same as $1 to be received one year from today? • Is $1 received today worth the same as $1 to be received one hundred years from today? • Why or why not? © Dale R. Geiger 2011 2

Terminal Learning Objective • Action: Calculate Present Or Future Value Of A Variety Of Cash Flow Scenarios • Condition: You are a cost advisor technician with access to all regulations/course handouts, and awareness of Operational Environment (OE)/Contemporary Operational Environment (COE) variables and actors • Standard: with at least 80% accuracy • Identify and enter relevant report data to solve Present and Future Value equations using macro enabled cash flow templates © Dale R. Geiger 2011 3

Time Value of Money Concepts Money received Today: Money received in the Future: • Can be invested Today to earn interest • Has not yet begun to earn interest • Can be spent Today at Today’s prices • Can be spent in the Future at inflated prices © Dale R. Geiger 2011 4

Simple Interest • Interest earned on Principal only Principal * Annual Interest Rate * Time in Years • Invest $1 today at 10% interest for 3 years Interest = $1 *. 10 * 3 = $. 30 • $1 grows to $1. 30 over 3 years © Dale R. Geiger 2011 5

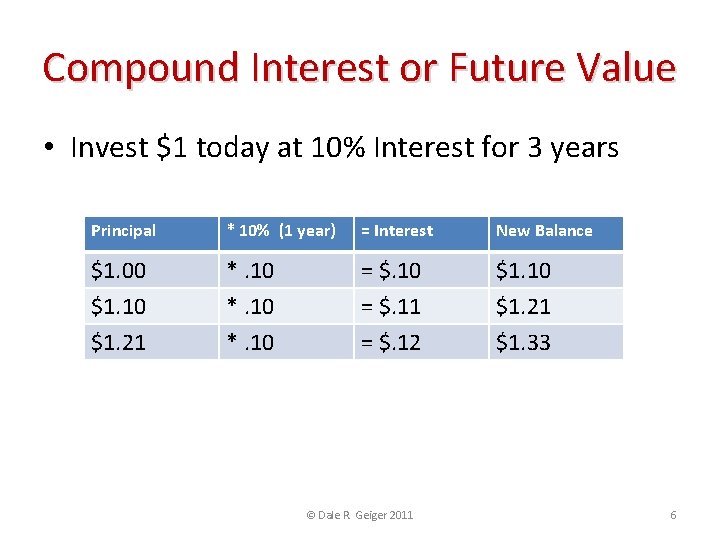
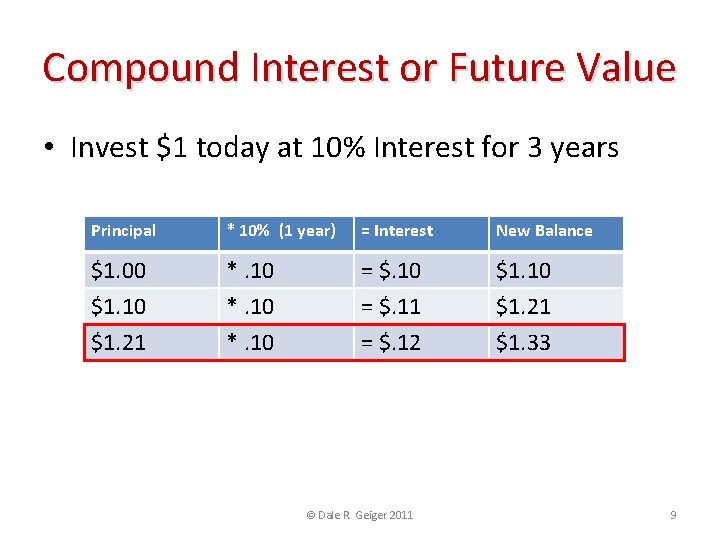
Compound Interest or Future Value • Invest $1 today at 10% Interest for 3 years Principal * 10% (1 year) = Interest New Balance $1. 00 $1. 10 $1. 21 *. 10 = $. 11 = $. 12 $1. 10 $1. 21 $1. 33 • This relationship can be expressed as: Principal * (1 + Annual Interest Rate)Time in Years $1*(1+. 10)3 = $1. 33 © Dale R. Geiger 2011 6

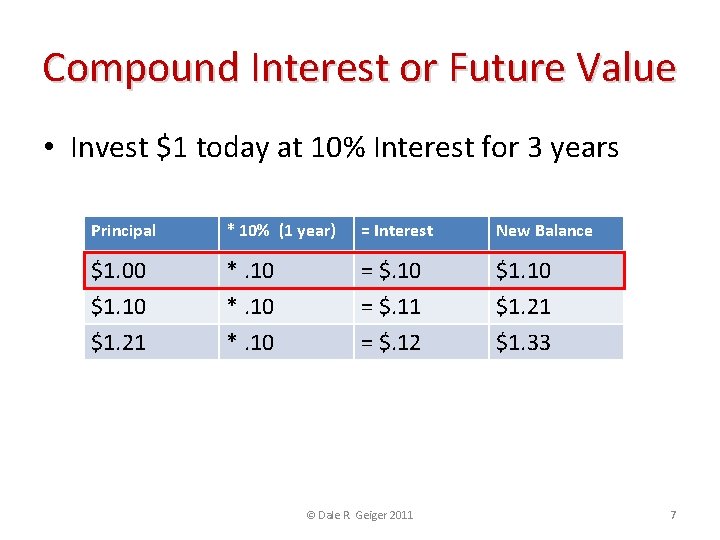
Compound Interest or Future Value • Invest $1 today at 10% Interest for 3 years Principal * 10% (1 year) = Interest New Balance $1. 00 $1. 10 $1. 21 *. 10 = $. 11 = $. 12 $1. 10 $1. 21 $1. 33 • This relationship can be expressed as: Principal * (1 + Annual Interest Rate)Time in Years $1*(1+. 10)3 = $1. 33 © Dale R. Geiger 2011 7

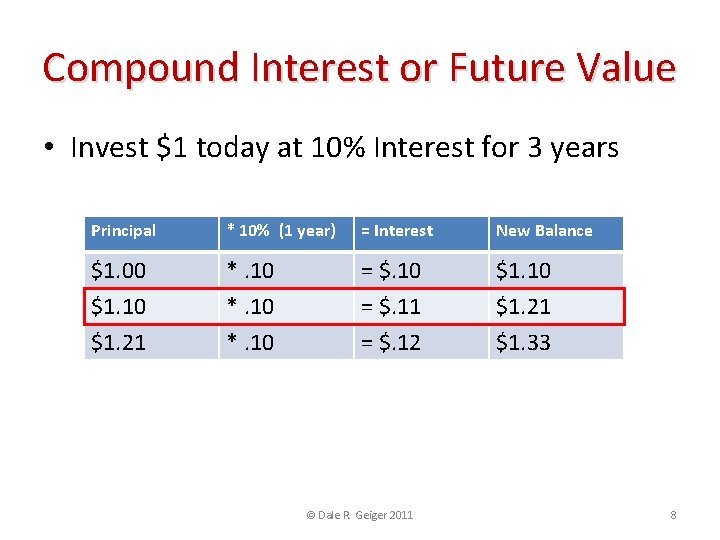
Compound Interest or Future Value • Invest $1 today at 10% Interest for 3 years Principal * 10% (1 year) = Interest New Balance $1. 00 $1. 10 $1. 21 *. 10 = $. 11 = $. 12 $1. 10 $1. 21 $1. 33 • This relationship can be expressed as: Principal * (1 + Annual Interest Rate)Time in Years $1*(1+. 10)3 = $1. 33 © Dale R. Geiger 2011 8

Compound Interest or Future Value • Invest $1 today at 10% Interest for 3 years Principal * 10% (1 year) = Interest New Balance $1. 00 $1. 10 $1. 21 *. 10 = $. 11 = $. 12 $1. 10 $1. 21 $1. 33 • This relationship can be expressed as: Principal * (1 + Annual Interest Rate)Time in Years $1*(1+. 10)3 = $1. 33 © Dale R. Geiger 2011 9

Compound Interest or Future Value • Invest $1 today at 10% Interest for 3 years Principal * 10% (1 year) = Interest New Balance $1. 00 $1. 10 $1. 21 *. 10 = $. 11 = $. 12 $1. 10 $1. 21 $1. 33 • This relationship can be expressed as: Principal * (1 + Annual Interest Rate)Time in Years $1*(1+. 10)3 = $1. 33 © Dale R. Geiger 2011 10

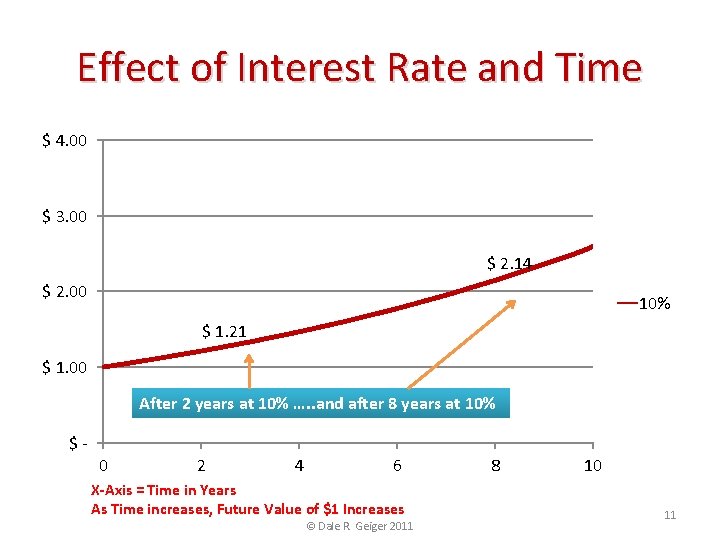
Effect of Interest Rate and Time $ 4. 00 $ 3. 00 $ 2. 14 $ 2. 00 10% $ 1. 21 $ 1. 00 After 2 years at 10% …. . and after 8 years at 10% $- 0 2 4 6 X-Axis = Time in Years As Time increases, Future Value of $1 Increases © Dale R. Geiger 2011 8 10 11

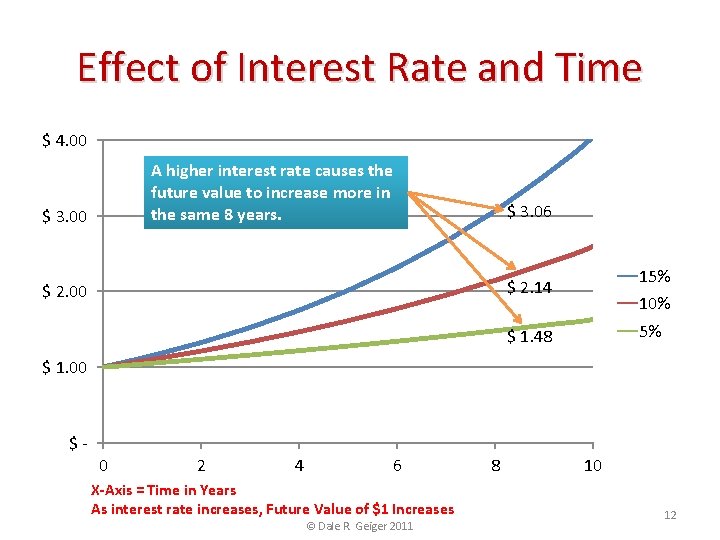
Effect of Interest Rate and Time $ 4. 00 A higher interest rate causes the future value to increase more in the same 8 years. $ 3. 00 $ 3. 06 15% $ 2. 14 $ 2. 00 10% 5% $ 1. 48 $ 1. 00 $- 0 2 4 6 X-Axis = Time in Years As interest rate increases, Future Value of $1 Increases © Dale R. Geiger 2011 8 10 12

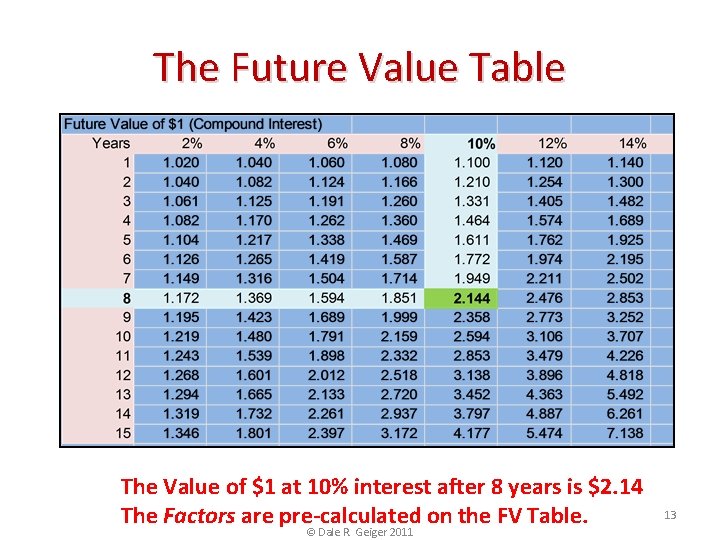
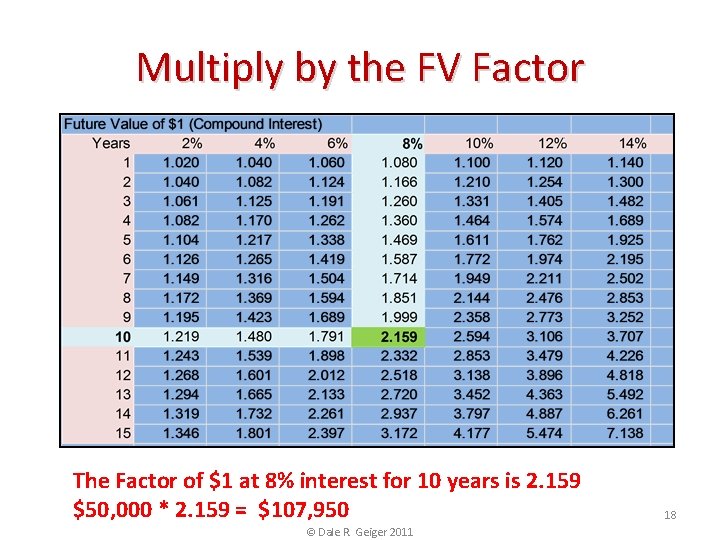
The Future Value Table The Value of $1 at 10% interest after 8 years is $2. 14 The Factors are pre-calculated on the FV Table. © Dale R. Geiger 2011 13

Check on Learning • How does compound interest differ from simple interest? • How does number of years affect the future value of an investment? © Dale R. Geiger 2011 14

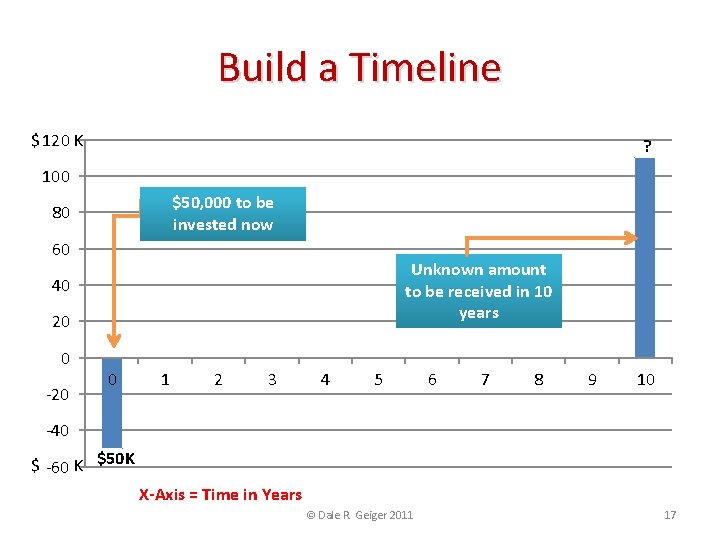
Demonstration Problem • If I invest $50, 000 today at 8%, what will it be worth in 10 years? • Steps: 1. Identify the key variables • Cash flow • Interest rate • Time in years 2. Build a timeline 3. Multiply cash flow by FV factor from the Table © Dale R. Geiger 2011 15

Identify Key Variables • Cash Flows • $50, 000 to be paid now • Cash Payments are negative numbers • Some unknown amount to be received ten years in the future • Cash Receipts are positive numbers • Interest Rate = 8% • Time in Years = 10 © Dale R. Geiger 2011 16

Build a Timeline $ 120 K ? 100 $50, 000 to be invested now 80 60 Unknown amount to be received in 10 years 40 20 0 -20 0 1 2 3 4 5 6 7 8 9 10 -40 $ -60 K $50 K X-Axis = Time in Years © Dale R. Geiger 2011 17

Multiply by the FV Factor The Factor of $1 at 8% interest for 10 years is 2. 159 $50, 000 * 2. 159 = $107, 950 © Dale R. Geiger 2011 18

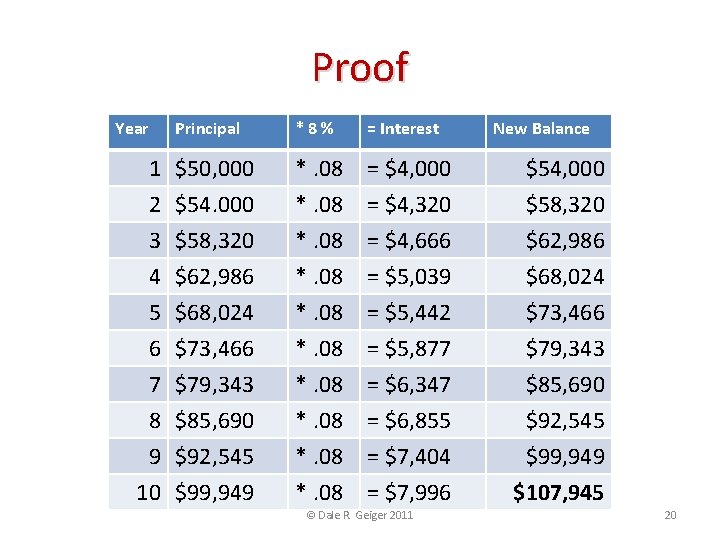
Using the Formula • The formula proves that the answer from the table is correct: $50, 000 * (1 +. 08)10 = $107, 946 • The difference of $4 is caused by rounding in the table © Dale R. Geiger 2011 19

Proof Year Principal 1 $50, 000 2 $54. 000 3 $58, 320 4 5 6 7 8 9 10 $62, 986 $68, 024 $73, 466 $79, 343 $85, 690 $92, 545 $99, 949 *8% = Interest *. 08 = $4, 000 = $4, 320 = $4, 666 $54, 000 $58, 320 $62, 986 *. 08 *. 08 = $5, 039 = $5, 442 = $5, 877 = $6, 347 = $6, 855 = $7, 404 = $7, 996 $68, 024 $73, 466 $79, 343 $85, 690 $92, 545 $99, 949 $107, 945 © Dale R. Geiger 2011 New Balance 20

Check on Learning • What is the first step in solving a future value problem? • How are cash payments represented in the timeline? © Dale R. Geiger 2011 21

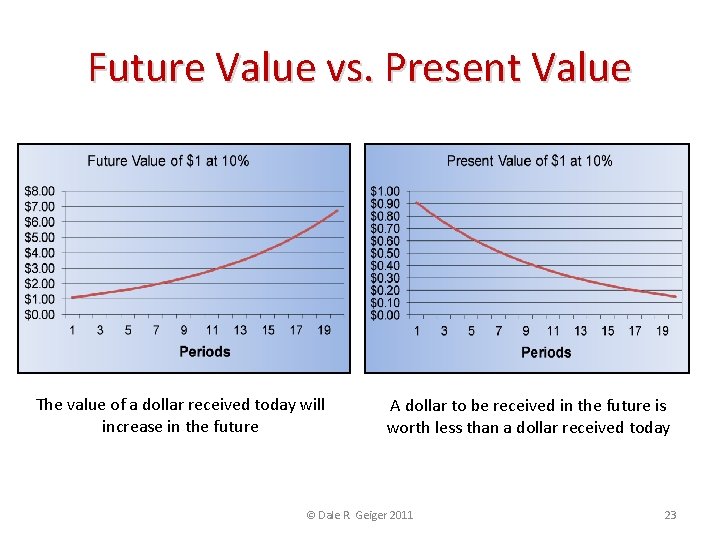
Future Value vs. Present Value • Future Value answers the question: • To what value will $1 grow in the Future? • Present Value answers the question: • What is the value Today of $1 to be received in the Future? -or • How much must be invested today to achieve $1 in the Future? © Dale R. Geiger 2011 22

Future Value vs. Present Value The value of a dollar received today will increase in the future A dollar to be received in the future is worth less than a dollar received today © Dale R. Geiger 2011 23

Present Value Concepts • What is the value Today of $1 to be received one year in the Future? • How much must be invested Today to grow to $1 one year from Today? • The answer to these two questions is the same! © Dale R. Geiger 2011 24

Present Value Concepts • Discount Rate represents interest or inflation • Assume a rate of 10% • What is the cost expression for this relationship? $Investment Today + Interest = $1. 00 -or$Investment + ($Investment *. 10) = $1. 00 $Investment * (1+. 10) = $1. 00 $Investment = $1/(1. 10) $Investment = $. 91 © Dale R. Geiger 2011 25

Present Value Concepts • Discount Rate represents interest or inflation • Assume a rate of 10% • What is the cost expression for this relationship? $Investment Today + Interest = $1. 00 -or$Investment + ($Investment *. 10) = $1. 00 $Investment * (1+. 10) = $1. 00 $Investment = $1/(1. 10) $Investment = $. 91 © Dale R. Geiger 2011 26

Present Value Concepts • Discount Rate represents interest or inflation • Assume a rate of 10% • What is the cost expression for this relationship? $Investment Today + Interest = $1. 00 -or$Investment + ($Investment *. 10) = $1. 00 $Investment * (1+. 10) = $1. 00 $Investment = $1/(1. 10) $Investment = $. 91 © Dale R. Geiger 2011 27

Present Value Concepts • Discount Rate represents interest or inflation • Assume a rate of 10% • What is the cost expression for this relationship? $Investment Today + Interest = $1. 00 -or$Investment + ($Investment *. 10) = $1. 00 $Investment * (1+. 10) = $1. 00 $Investment = $1/(1. 10) $Investment = $. 91 © Dale R. Geiger 2011 28

Present Value Concepts • Discount Rate represents interest or inflation • Assume a rate of 10% • What is the cost expression for this relationship? $Investment Today + Interest = $1. 00 -or$Investment + ($Investment *. 10) = $1. 00 $Investment * (1+. 10) = $1. 00 $Investment = $1/(1. 10) $Investment = $. 91 © Dale R. Geiger 2011 29

Proof • Plug $. 91 in to the original equation: $. 91 + ($. 91 *. 10) = $1. 00 $. 91 +. 09 = $1. 00 • This relationship is fairly simple for one period, but what about multiple periods? © Dale R. Geiger 2011 30

Present Value Concepts • How much must be invested today to achieve $1. 00 three years from today? • What is the cost expression for this relationship? $Investment * (1 + Rate) #Years = $Future Value $Investment = $Future Value / (1 + Rate) #Years -or$Investment * (1+. 10) 3 = $1. 00 $Investment = $1. 00 / (1+. 10) 3 $Investment = $. 75 © Dale R. Geiger 2011 31

Present Value Concepts • How much must be invested today to achieve $1. 00 three years from today? • What is the cost expression for this relationship? $Investment * (1 + Rate) #Years = $Future Value $Investment = $Future Value / (1 + Rate) #Years -or$Investment * (1+. 10) 3 = $1. 00 $Investment = $1. 00 / (1+. 10) 3 $Investment = $. 75 © Dale R. Geiger 2011 32

Present Value Concepts • How much must be invested today to achieve $1. 00 three years from today? • What is the cost expression for this relationship? $Investment * (1 + Rate) #Years = $Future Value $Investment = $Future Value / (1 + Rate) #Years -or$Investment * (1+. 10) 3 = $1. 00 $Investment = $1. 00 / (1+. 10) 3 $Investment = $. 75 © Dale R. Geiger 2011 33

Present Value Concepts • The Investment amount is known as the Present Value • The Present Value relationship is expressed in the formula: Future Cash Flow * 1/(1 + Rate) #Years -or$1 * 1/(1. 10)3 = $. 75 © Dale R. Geiger 2011 34

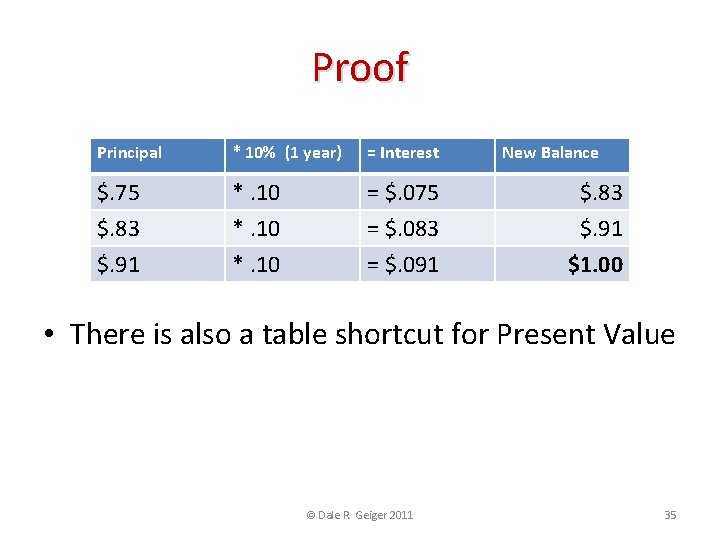
Proof Principal * 10% (1 year) = Interest $. 75 $. 83 $. 91 *. 10 = $. 075 = $. 083 = $. 091 New Balance $. 83 $. 91 $1. 00 • There is also a table shortcut for Present Value © Dale R. Geiger 2011 35

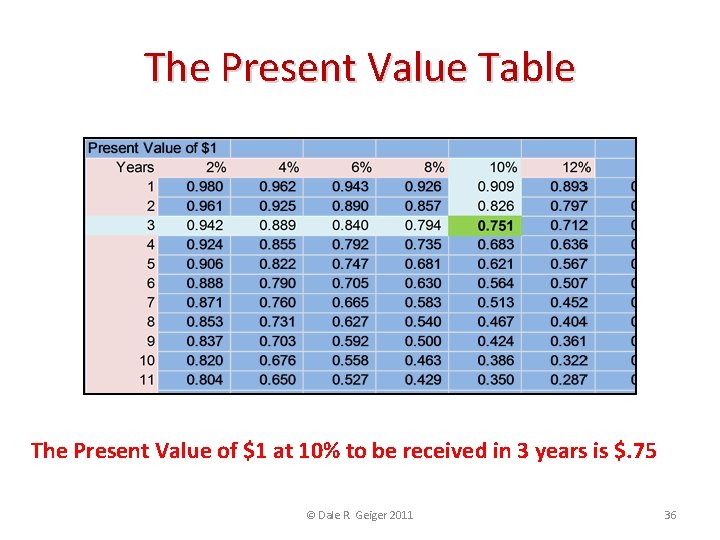
The Present Value Table The Present Value of $1 at 10% to be received in 3 years is $. 75 © Dale R. Geiger 2011 36

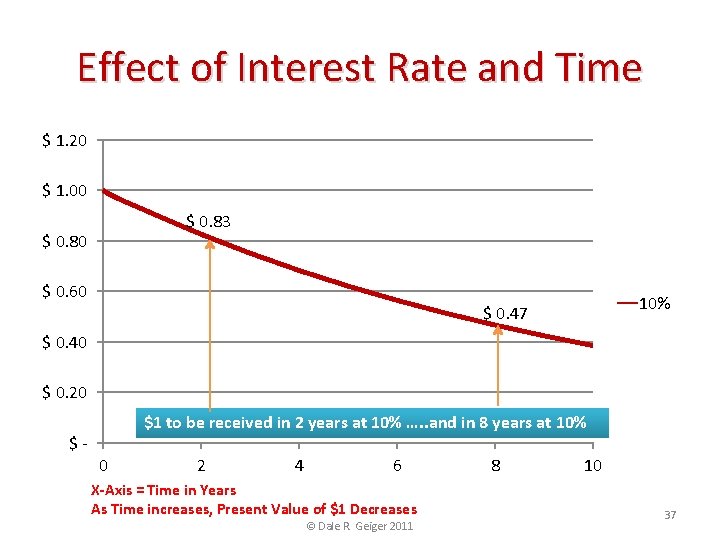
Effect of Interest Rate and Time $ 1. 20 $ 1. 00 $ 0. 83 $ 0. 80 $ 0. 60 10% $ 0. 47 $ 0. 40 $ 0. 20 $- $1 to be received in 2 years at 10% …. . and in 8 years at 10% 0 2 4 6 X-Axis = Time in Years As Time increases, Present Value of $1 Decreases © Dale R. Geiger 2011 8 10 37

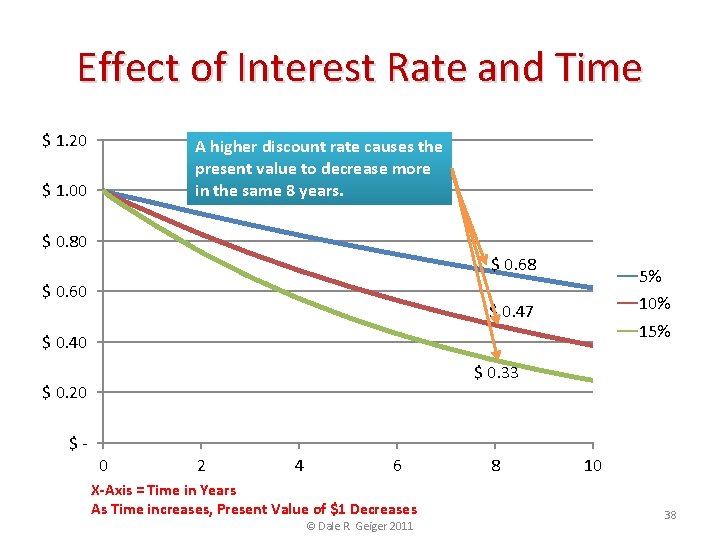
Effect of Interest Rate and Time $ 1. 20 A higher discount rate causes the present value to decrease more in the same 8 years. $ 1. 00 $ 0. 80 $ 0. 68 $ 0. 60 5% 10% $ 0. 47 15% $ 0. 40 $ 0. 33 $ 0. 20 $- 0 2 4 6 X-Axis = Time in Years As Time increases, Present Value of $1 Decreases © Dale R. Geiger 2011 8 10 38

Check on Learning • What does Present Value represent? • How does the Present Value table differ from the Future Value table? © Dale R. Geiger 2011 39

Demonstration Problem • What is the Present Value of a $60, 000 cash flow to be received 6 years from today assuming 12% discount rate? • Steps: 1. Identify the key variables • Cash flow • Discount rate • Time in years 2. Build a timeline 3. Multiply cash flow by the Factor from the PV Table © Dale R. Geiger 2011 40

Identify Key Variables • Cash Flow • $60, 000 to be received in the Future • Is equal to some unknown amount Today • Discount Rate = 12% • Time in Years = 6 © Dale R. Geiger 2011 41

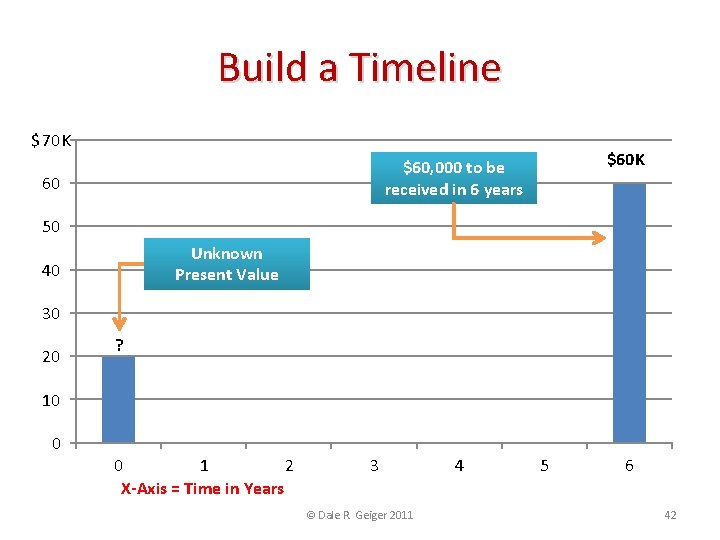
Build a Timeline $ 70 K $60, 000 to be received in 6 years 60 50 Unknown Present Value 40 30 20 ? 10 0 0 1 2 X-Axis = Time in Years 3 © Dale R. Geiger 2011 4 5 6 42

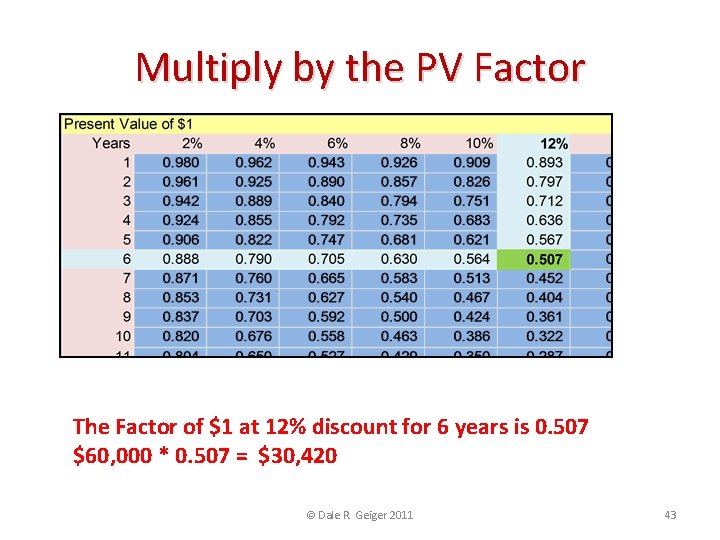
Multiply by the PV Factor The Factor of $1 at 12% discount for 6 years is 0. 507 $60, 000 * 0. 507 = $30, 420 © Dale R. Geiger 2011 43

Using the Formula • The formula proves that the answer from the table is correct: $60, 000 * 1/(1 +. 12)6 = $30, 398 • The difference of $22 is caused by rounding in the table © Dale R. Geiger 2011 44

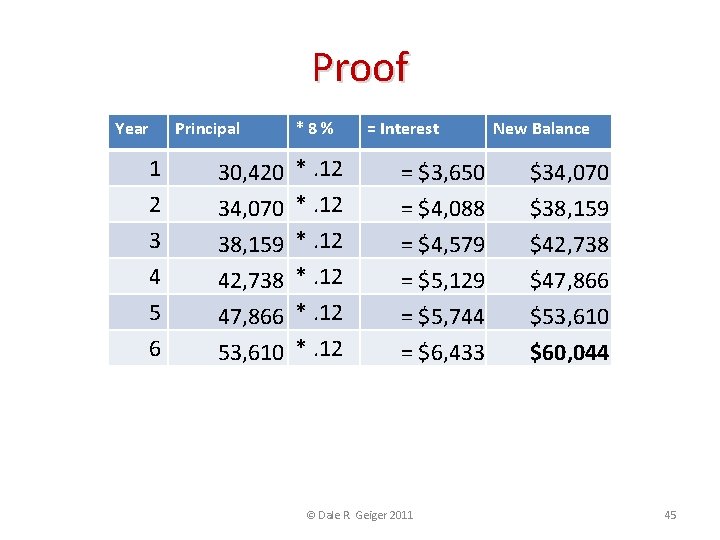
Proof Year 1 2 3 4 5 6 Principal 30, 420 34, 070 38, 159 42, 738 47, 866 53, 610 *8% *. 12 = Interest = $3, 650 = $4, 088 = $4, 579 = $5, 129 = $5, 744 = $6, 433 © Dale R. Geiger 2011 New Balance $34, 070 $38, 159 $42, 738 $47, 866 $53, 610 $60, 044 45

Check on Learning • How does time affect the present value of a cash flow? • How does the discount rate affect the present value of a cash flow? © Dale R. Geiger 2011 46

Practical Exercise © Dale R. Geiger 2011 47

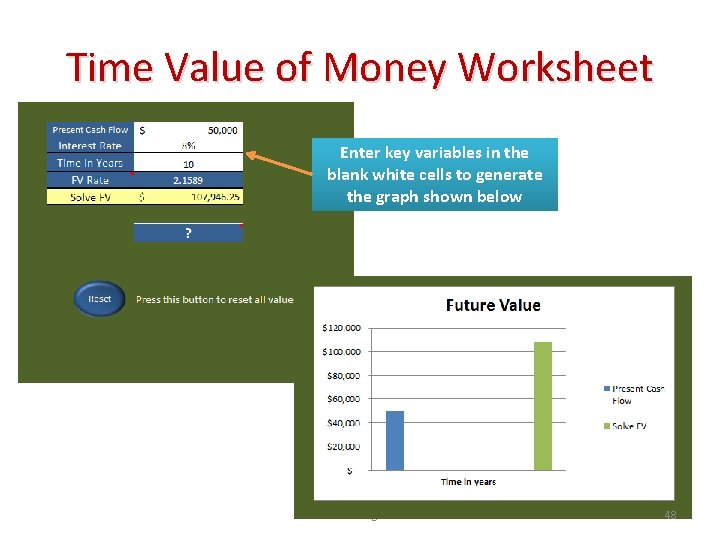
Time Value of Money Worksheet Enter key variables in the blank white cells to generate the graph shown below © Dale R. Geiger 2011 48

Time Value of Money Worksheet The spreadsheet tool also calculates Present Value © Dale R. Geiger 2011 49

Practical Exercise © Dale R. Geiger 2011 50
 Future value of multiple cash flows example
Future value of multiple cash flows example Future value of multiple cash flows example
Future value of multiple cash flows example Raw materials budget example
Raw materials budget example Incremental cash flow
Incremental cash flow How to calculate incremental cash flows
How to calculate incremental cash flows Future value of $1
Future value of $1 Diferencia entre future perfect y future perfect continuous
Diferencia entre future perfect y future perfect continuous Future perfect simple continuous
Future perfect simple continuous How to calculate future value of money
How to calculate future value of money Pv of cash flows formula
Pv of cash flows formula Incremental cash flow
Incremental cash flow Payback method formula
Payback method formula Cash flow indirect method
Cash flow indirect method Incremental cash flow
Incremental cash flow Examples of incremental cash flows
Examples of incremental cash flows Statement of cash flows order
Statement of cash flows order What are plant assets
What are plant assets Cash flow pro forma
Cash flow pro forma Prepaid expenses statement of cash flows
Prepaid expenses statement of cash flows The statement of cash flows reports
The statement of cash flows reports Capital budgeting
Capital budgeting Cash is current asset or not
Cash is current asset or not What are the cash flows from granting credit
What are the cash flows from granting credit Chapter 23 statement of cash flows
Chapter 23 statement of cash flows Relevant cash flows definition
Relevant cash flows definition The statement of cash flows classifies items as
The statement of cash flows classifies items as Chapter 13 statement of cash flows
Chapter 13 statement of cash flows Flow chapter 13
Flow chapter 13 Statement of cash flows partial
Statement of cash flows partial Relevant cash flow
Relevant cash flow Destiny corporation is preparing its
Destiny corporation is preparing its Incremental cash flows example
Incremental cash flows example Managing operating exposure
Managing operating exposure Intermediate cash flows
Intermediate cash flows What is effective rate of interest
What is effective rate of interest Cash received from customers
Cash received from customers The statement of cash flows helps users
The statement of cash flows helps users Intermediate accounting chapter 23
Intermediate accounting chapter 23 Profitability index
Profitability index Present value of perpetuity
Present value of perpetuity Value creation value delivery value capture
Value creation value delivery value capture Present and future value of money
Present and future value of money Cash to cash cycle time
Cash to cash cycle time Cash to cash cycle time
Cash to cash cycle time Cash-in cash-out
Cash-in cash-out Paid cash to replenish the petty cash fund
Paid cash to replenish the petty cash fund A computerized cash payments system that transfers funds
A computerized cash payments system that transfers funds Present simple present continuous past simple
Present simple present continuous past simple Present simple timetables
Present simple timetables Past simple future
Past simple future Past simple future simple present simple
Past simple future simple present simple