Topics Covered Future Values Present Values Multiple Cash



































- Slides: 37

Topics Covered • • • Future Values Present Values Multiple Cash Flows Perpetuities and Annuities Inflation & Time Value

Future Values Example - Simple Interest earned at a rate of 6% for five years on a principal balance of £ 100. Today Interest Earned Value 100 1 6 106 Future Years 2 3 4 5 6 6 112 118 124 130 Value at the end of Year 5 = £ 130

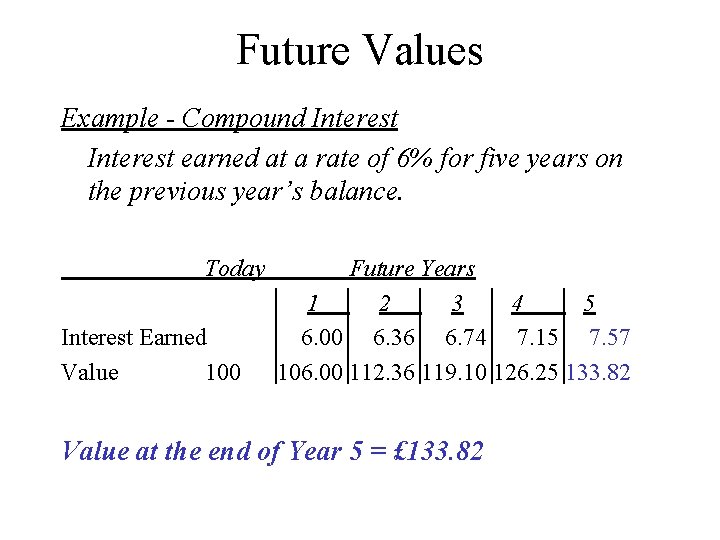
Future Values Example - Compound Interest earned at a rate of 6% for five years on the previous year’s balance. Today Interest Earned Value 100 Future Years 1 2 3 4 5 6. 00 6. 36 6. 74 7. 15 7. 57 106. 00 112. 36 119. 10 126. 25 133. 82 Value at the end of Year 5 = £ 133. 82

Future Values Example - FV What is the future value of £ 100 if interest is compounded annually at a rate of 6% for five years?

Manhattan Island Sale Peter Minuit bought Manhattan Island for £ 16 in 1626. Was this a good deal? To answer, determine £ 16 is worth in the year 2001, compounded at 8% and 5%.

Present Values • Present Value: Value today of a future cash flow • Discount Rate: Interest used to calculate value of future cash flows.

Present Values

Present Values Example You just bought a new computer for $3, 000. The payment terms are 2 years same as cash. If you can earn 8% on your money, how much money should you set aside today in order to make the payment when due in two years?

Time Value of Money (applications) • The PV formula has many applications. Given any variables in the equation, you can solve for the remaining variable.

PV of Multiple Cash Flows Example Your auto dealer gives you the choice to pay $15, 500 cash now, or make three payments: $8, 000 now and $4, 000 at the end of the following two years. If your cost of money is 8%, which do you prefer?

PV of Multiple Cash Flows • PVs can be added together to evaluate multiple cash flows.

Perpetuities & Annuities Perpetuity A stream of level cash payments that never ends. Annuity Equally spaced level stream of cash flows for a limited period of time.

Perpetuities & Annuities Example - Perpetuity In order to create an endowment, which pays £ 100, 000 per year, forever, how much money must be set aside today in the rate of interest is 10%?

Perpetuities & Annuities Example - Perpetuity In order to create an endowment, which pays £ 100, 000 per year, forever, how much money must be set aside today in the rate of interest is 10%?

Perpetuities & Annuities PV of Annuity Formula C = cash payment r = interest rate t = Number of years cash payment is received

Arbitrage • You are given the following prices Pt today for receiving risk free £ 1 payments t periods from now. T= Pt = 1 0. 95 2 0. 9 3 0. 95 • How would you make a lot of money?

Compounding • Natwest is offering loans at 10% interest compounded quarterly. • Barclays is offering loans at 10. 5% interest compounded annually. • Which would you take?

Compounding Formula • General Formula is • Continuous is Why? Look at % increase (slope/value) • What is continuous rate for 10% annual? • How long would it take to double your money?

Mortgage payments • You want to buy a home for £ 100, 000. • Natwest offers you a mortgage: 0 down, 10% a year for 25 years. • How much must you pay per year?

Save and Retire. • You plan to save £ 4, 000 every year for 20 years and then retire. Given a 10% rate of interest, what will be the FV of your retirement account?

Growth and Perpetuities • What is the present value of a perpetuity whose payment grows at a rate of (1+g) per year?

Inflation - Rate at which prices as a whole are increasing. Nominal Interest Rate - Rate at which money invested grows. Real Interest Rate - Rate at which the purchasing power of an investment increases.

Inflation approximation formula

Bonds Terminology • Bond - Security that obligates the issuer to make specified payments to the bondholder. • Coupon - The interest payments made to the bondholder. • Face Value (Par Value or Maturity Value) - Payment at the maturity of the bond. • Coupon Rate - Annual interest payment, as a percentage of face value.

Bonds WARNING The coupon rate IS NOT the discount rate used in the Present Value calculations. The coupon rate merely tells us what cash flow the bond will produce. Since the coupon rate is listed as a %, this misconception is quite common.

Bond Pricing The price of a bond is the Present Value of all cash flows generated by the bond (i. e. coupons and face value) discounted at the required rate of return.

Bond Sensitivity • A zero coupon bond pays £ 10000 in 10 years time. • What is the PV of the bond if interest is 10% annual? • What is the PV of the bond if interest falls to 9% annual?

Bond Pricing The price of a bond is the Present Value of all cash flows generated by the bond (i. e. coupons and face value) discounted at the required rate of return.

Bond Pricing • What is the price of a 6 % annual coupon bond, with a $1, 000 face value, which matures in 3 years? Assume a required return of 5%. • What is the price if the return is 6%

Bond Yields • Current Yield - Annual coupon payments divided by bond price. • Yield To Maturity - Interest rate for which the present value of the bond’s payments equal the price.

Bond Yields Calculating Yield to Maturity (YTM=r) If you are given the price of a bond (PV) and the coupon rate, the yield to maturity can be found by solving for r.

Interest Rate Risk Premium Bond Discount Bond

Interest Rate Risk 30 yr bond 3 yr bond

Default Risk • • Credit risk Default premium Investment grade Junk bonds

Default Risk

Corporate Bonds • Zero coupons • Floating rate bonds • Convertible bonds

The Yield Curve Term Structure of Interest Rates - A listing of bond maturity dates and the interest rates that correspond with each date. Yield Curve - Graph of the term structure. Question: If you knew interest rates won’t change from now until one year from now, what would that mean about the yield curve of US treasury bonds?