Zefry Darmawan ST MT Program Studi Teknik Industri

Zefry Darmawan, ST, MT Program Studi Teknik Industri Universitas Brawijaya Malang 2012 MATRIKS NONSINGULAR

Definisi Matriks singular Sebuah matriks A adalah matriks persegi dengan ketentuan AB = In = BA Matriks B adalah invers dari matriks A, jika matriks A tidak memiliki invers maka disebut matriks singular.

Aturan invers Jika matriks A memiliki invers berupa matriks B dan C, kemudian B = C, maka AB = In = BA dan AC = In = CA Kemudian B(AC) = BIn = B dan (BA)C = In. C = C Maka berlaku: 1. AA-1 = In = A-1 A 2. (A-1)-1 = A 3. (AB)-1 = B-1 A-1

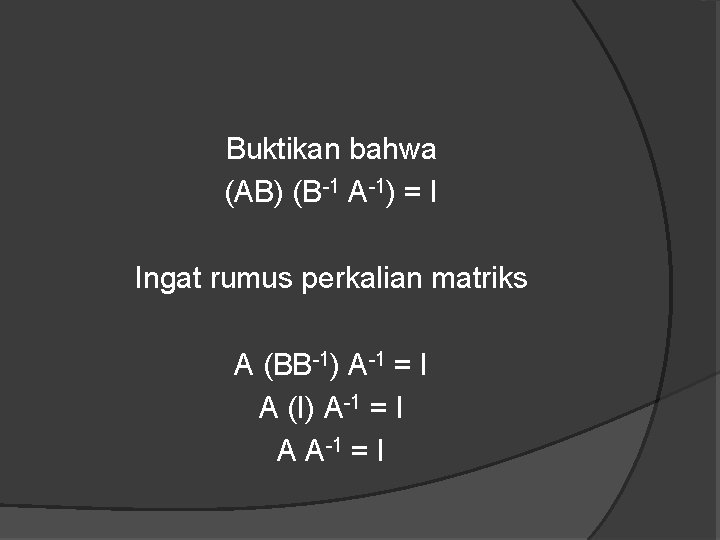
Buktikan bahwa (AB) (B-1 A-1) = I Ingat rumus perkalian matriks A (BB-1) A-1 = I A (I) A-1 = I A A-1 = I

Teorema 1 Jika

Teorema 2 Jika AX = B, maka X = A-1 B Dengan asumsi matriks A memiliki invers, maka penyelesaian : 1. Uniqueness AX = B (A-1 A) X = A-1 B In X = A-1 B 2. Existence jika X = A-1 B, maka AX = A(A-1 B) (A A-1) B = In B = B

Teori Cramer ax + by = e cx + dy = f Jika ada 2 persamaan dengan banyak variabel tidak diketahui nilainya, dan jika maka dimana

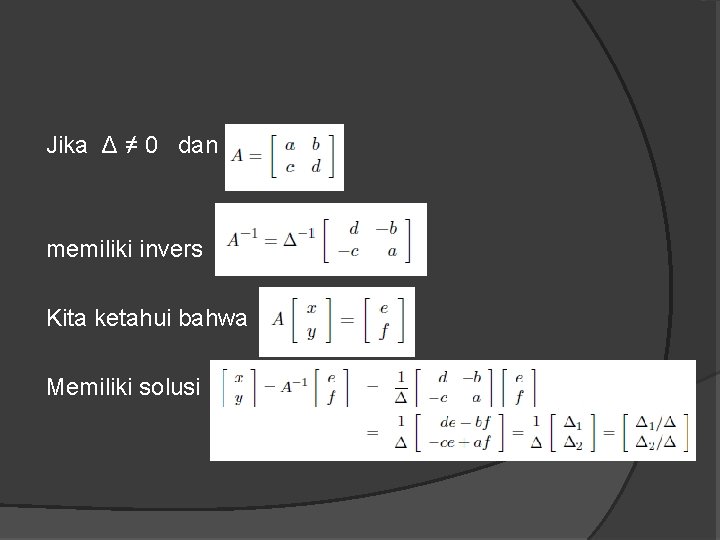
Jika Δ ≠ 0 dan memiliki invers Kita ketahui bahwa Memiliki solusi

Contoh soal 7 x + 8 y = 100 2 x – 9 y = 10 Memiliki penyelesaian Sehingga x = -980/-79 = 980/79 y = -130/-79 = 130/79

Jika A adalah matriks non singular dan AX = 0 hanya akan memiliki satu trivial solution, maka akan sama dengan Jika AX = 0 , tidak memiliki trivial solution maka A adalah matriks singular Bukti Jika A non singular, dan AX = 0, maka X = A-1 0 = 0

Matriks Baris Elementer Ada 3 jenis baris elementer: 1. Eij (i ≠ j) diperoleh dari matriks identitas I dengan menukar baris i dan kolom j secara bergantian. 2. Ei (t), (t ≠ 0) diperoleh dengan mengalikan baris ke-i dari matriks I dengan ( t ). 3. Eij (t), (i ≠ j) diperoleh dari matriks I dengan menambahkan sebanyak t-kali pada kolom ke-j matriks I ke baris ke-i.

Jenis-jenis baris elementer Baris elementer non singular terdiri dari: 1. Ei j-1 = Ei j 2. (Ei (t))-1 = Ei(t-1) 3. (Ei j(t))-1 = Ei j (-t) Pembuktian -1

Contoh soal Tentukan matriks A = E 3(5)E 23(2)E 12 Tentukan pula A-1 Mencari A-1

2 Matriks ekuivalen baris A dan B adalah matriks ekuivalen baris, jika matriks B diperoleh dari matriks A dengan melakukan proses transformasi baris. Dan jika E 1. . . Er adalah elemen-elemen baris yang saling berkorespondensi. Maka: B = Er (. . . (E 2(E 1 A)). . . ) = (Er. . . E 1)A = PA Dimana P = Er. . . E 1 adalah non singular

Operasi Baris Elementer Jika A adalah matriks berordo nxn dan sehingga apabila A adalah ekuivalen baris terhadap matriks I dan A adalah matriks non singular. Maka A-1 dapat diperoleh melalui Operasi baris matriks A yang dirubah menjadi matriks I Er. . . E 1 A = I B = Er. . . E 1 adalah non singular B-1 (BA) = B-1 I sehingga A = B-1 Tentu saja jika A-1 = (B-1)-1 = B = Er((. . . (E 1 I). . . ) sehingga A-1 akan diperoleh dari I dengan melakukan proses transformasi baris elementer untuk mengubah A menjadi I

Contoh soal baris elementer Jika matriks non singular tentukan A-1 Menggunakan operasi baris elementer Solusi :

Transpose Matriks Jika A adalah matriks berordo mxn , sehingga AT adalah transpose dari matriks A dengan cara menukar elemen baris menjadi elemen kolom A = [aij] sehingga (AT)ji = aij Sifat transpose matriks: 1. (AT)T = A 2. (A ± B)T = AT ± BT jika A dan B berordo mxn 3. (s A)T = s AT, dengan a adalah skalar 4. (AB)T = BT AT jika A berordo mxn dan B nxp 5. (AT)-1 = (A-1)T, jika A dan AT non singular

Matriks simetris Matriks A dikatakan simetris jika AT = A aji = aij Matriks A merupakan matriks persegi berordo (nxn) Contoh:

Matriks Skew-Simetris Matriks A disebut skew-simetris jika AT = -A aji = -aij Matriks A merupakan matriks persegi berordo (nxn) Contoh :

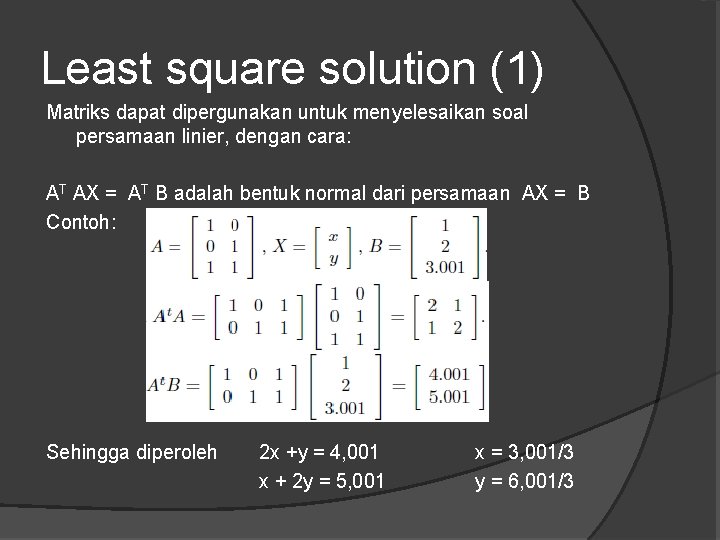
Least square solution (1) Matriks dapat dipergunakan untuk menyelesaikan soal persamaan linier, dengan cara: AT AX = AT B adalah bentuk normal dari persamaan AX = B Contoh: Sehingga diperoleh 2 x +y = 4, 001 x + 2 y = 5, 001 x = 3, 001/3 y = 6, 001/3

Least square solution (2) Jika terdapat titik (x 1, y 1), . . . , (xn, yn) dan titik-titik tersebut terletak pada persamaan garis y = mx + c Maka dengan metode least square diperoleh: Ax = B, dimana Dengan persamaan normal berbentuk (AT A)X = AT B

Least square solution (3) Dengan bentuk dari

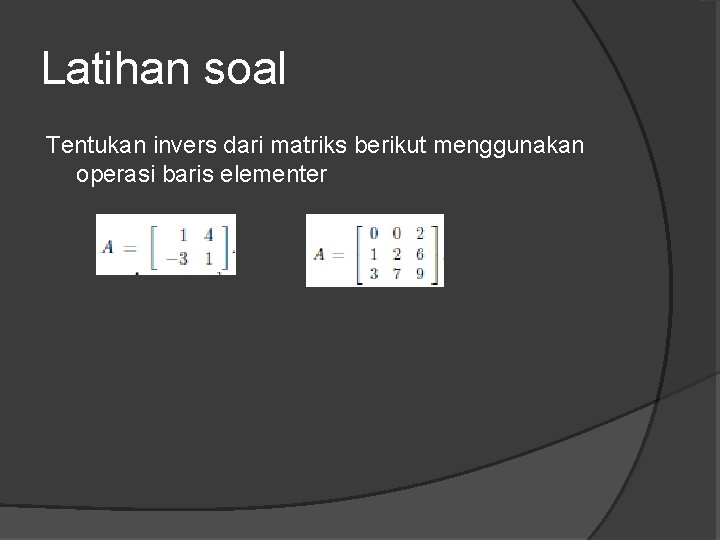
Latihan soal Tentukan invers dari matriks berikut menggunakan operasi baris elementer