LowPower Design of Digital VLSI Circuits GateLevel Power

Low-Power Design of Digital VLSI Circuits Gate-Level Power Analysis Vishwani D. Agrawal James J. Danaher Professor Dept. of Electrical and Computer Engineering Auburn University, Auburn, AL 36849 vagrawal@eng. auburn. edu http: //www. eng. auburn. edu/~vagrawal Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 1

Power Analysis l Motivation: l Specification l Optimization l Reliability l Applications l Design analysis and optimization l Physical design l Packaging l Test Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 2

Abstraction, Complexity, Accuracy Abstraction level Algorithm Computing resources Analysis accuracy Least Worst Most Best Software and system Hardware behavior Register transfer Logic Circuit Device Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 3

Spice l Circuit/device level analysis Circuit modeled as network of transistors, capacitors, resistors and voltage/current sources. l Node current equations using Kirchhoff’s current law. l Average and instantaneous power computed from supply voltage and device current. l l Analysis is accurate but expensive l l Used to characterize parts of a larger circuit. Original references: L. W. Nagel and D. O. Pederson, “SPICE – Simulation Program With Integrated Circuit Emphasis, ” Memo ERL-M 382, EECS Dept. , University of California, Berkeley, Apr. 1973. l L. W. Nagel, SPICE 2, A Computer program to Simulate Semiconductor Circuits, Ph. D Dissertation, University of California, Berkeley, May 1975. l Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 4

Logic Model of MOS Circuit p. MOS FETs a b VDD Ca Cc Cb n. MOS FETs Cd Ca , Cb , Cc and Cd are node capacitances Copyright Agrawal, 2007 c a Da b Db c Dc Da and Db are interconnect or propagation delays Dc is inertial delay of gate Lectures 5 -8: Power Analysis 5

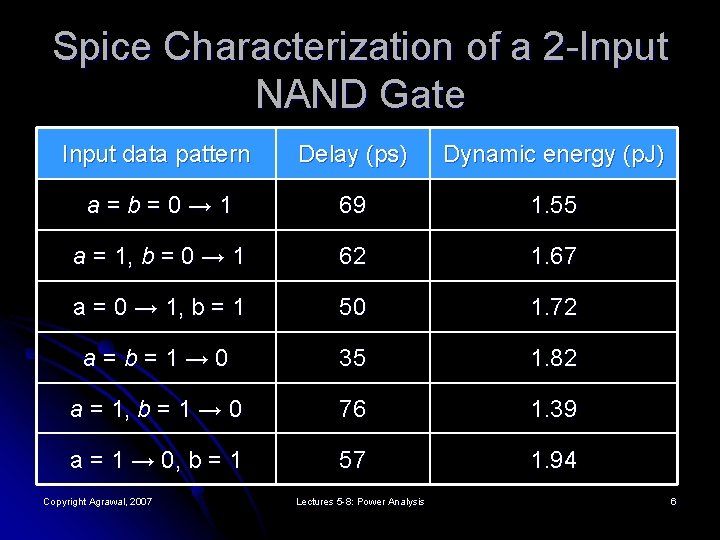
Spice Characterization of a 2 -Input NAND Gate Input data pattern Delay (ps) Dynamic energy (p. J) a=b=0→ 1 69 1. 55 a = 1, b = 0 → 1 62 1. 67 a = 0 → 1, b = 1 50 1. 72 a=b=1→ 0 35 1. 82 a = 1, b = 1 → 0 76 1. 39 a = 1 → 0, b = 1 57 1. 94 Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 6

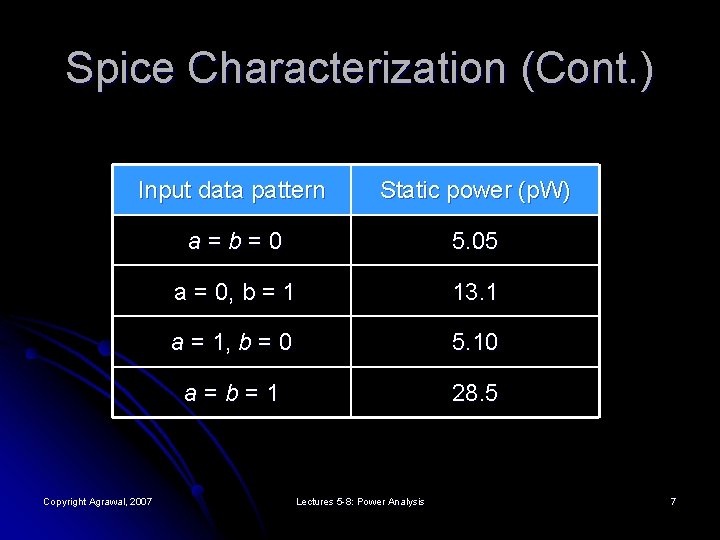
Spice Characterization (Cont. ) Input data pattern Static power (p. W) a=b=0 5. 05 a = 0, b = 1 13. 1 a = 1, b = 0 5. 10 a=b=1 28. 5 Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 7

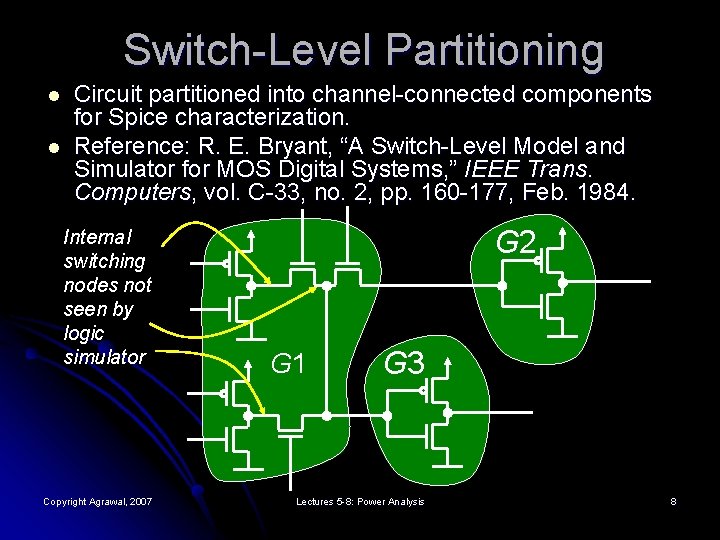
Switch-Level Partitioning l l Circuit partitioned into channel-connected components for Spice characterization. Reference: R. E. Bryant, “A Switch-Level Model and Simulator for MOS Digital Systems, ” IEEE Trans. Computers, vol. C-33, no. 2, pp. 160 -177, Feb. 1984. Internal switching nodes not seen by logic simulator Copyright Agrawal, 2007 G 2 G 1 G 3 Lectures 5 -8: Power Analysis 8

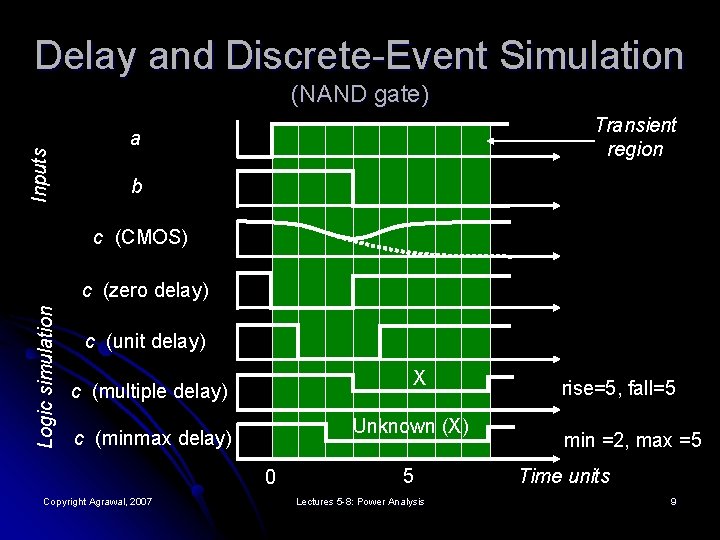
Delay and Discrete-Event Simulation Inputs (NAND gate) Transient region a b c (CMOS) Logic simulation c (zero delay) c (unit delay) X c (multiple delay) Unknown (X) c (minmax delay) 0 Copyright Agrawal, 2007 5 Lectures 5 -8: Power Analysis rise=5, fall=5 min =2, max =5 Time units 9

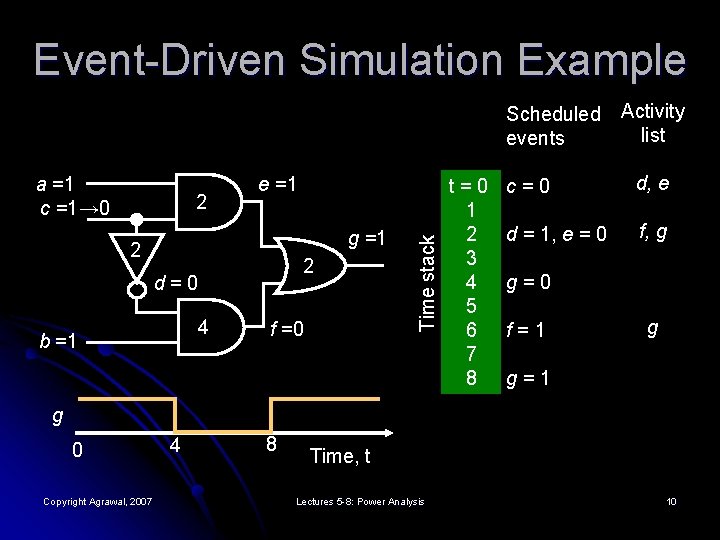
Event-Driven Simulation Example Scheduled events 2 e =1 g =1 2 2 d=0 4 b =1 f =0 Time stack a =1 c =1→ 0 t=0 1 2 3 4 5 6 7 8 Activity list c=0 d, e d = 1, e = 0 f, g g=0 f=1 g g=1 g 0 Copyright Agrawal, 2007 4 8 Time, t Lectures 5 -8: Power Analysis 10

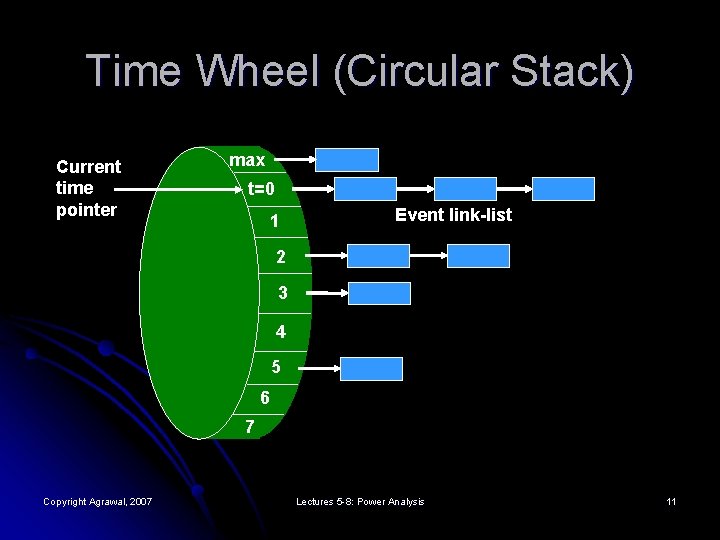
Time Wheel (Circular Stack) Current time pointer max t=0 1 Event link-list 2 3 4 5 6 7 Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 11

Gate-Level Power Analysis l Pre-simulation analysis: l Partition circuit into channel connected components. l Determine node capacitances from layout analysis (accurate) or from wire-load model* (approximate). l Determine dynamic and static power from Spice for each gate. l Determine gate delays using Spice or Elmore delay model. * Wire-load model estimates capacitance of a net by its pin-count. See Yeap, p. 39. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 12

Elmore Delay Model l W. Elmore, “The Transient Response of Damped Linear Networks with Particular Regard to Wideband Amplifiers, ” J. Appl. Phys. , vol. 19, no. 1, pp. 55 -63, Jan. 1948. 2 R 2 C 2 1 R 1 s 4 R 4 C 1 Shared resistance: C 4 R 3 3 C 3 R 45 = R 1 + R 3 R 15 = R 1 R 34 = R 1 + R 3 Copyright Agrawal, 2007 R 5 5 C 5 Lectures 5 -8: Power Analysis 13

Elmore Delay Formula N Delay at node k = 0. 69 Σ Cj × Rjk j=1 where N = number of capacitive nodes in the network Example: Delay at node 5 = 0. 69[R 1 C 1 + R 1 C 2 + (R 1+R 3)C 3 + (R 1+R 3)C 4 + (R 1+R 3+R 5)C 5] Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 14

Gate-Level Power Analysis (Cont. ) l l Run discrete-event (event-driven) logic simulation with a set of input vectors. Monitor the toggle count of each net and obtain capacitive component of power dissipation: Pcap = Σ Ck V 2 f all nodes k l Where: Ck is the total node capacitance being switched, as determined by the simulator. l V is the supply voltage. l f is the clock frequency, i. e. , the number of vectors applied per unit time l Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 15

Gate-Level Power Analysis (Cont. ) l Monitor dynamic energy events at the input of each gate and obtain internal switching (short circuit) power dissipation: Pint = Σ Σ E(g, e) F(g, e) gates g events e l Where l E(g, e) = energy of event e of gate g, pre-computed short-circuit power from Spice. l F(g, e) = occurrence frequency of the event e at gate g, observed by logic simulation. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 16

Gate-Level Power Analysis (Cont. ) l Monitor the static power dissipation state of each gate and obtain the static power dissipation: Pstat = Σ gates g l Σ P(g, s) T(g, s)/ T states s Where P(g, s) = static power dissipation of gate g for state s, obtained from Spice. l T(g, s) = duration of state s at gate g, obtained from logic simulation. l T = number of vectors × vector period. l Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 17

Gate-Level Power Analysis l Sum up all three components of power: l P = Pcap + Pint + Pstat References: A. Deng, “Power Analysis for CMOS/Bi. CMOS Circuits, ” Proc. International Workshop Low Power Design, 1994. l J. Benkoski, A. C. Deng, C. X. Huang, S. Napper and J. Tuan, “Simulation Algorithms, Power Estimation and Diagnostics in Power. Mill, ” Proc. PATMOS, 1995. l C. X. Huang, B. Zhang, A. C. Deng and B. Swirski, “The Design and Implementation of Power. Mill, ” Proc. International Symp. Low Power Design, 1995, pp. 105 -109. l Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 18

Probabilistic Analysis l View signals as a random processes Prob{s(t) = 1} = p 1 p 0 = 1 – p 1 C 0→ 1 transition probability = (1 – p 1) p 1 Power, P = (1 – p 1) p 1 CV 2 fck Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 19

Source of Inaccuracy p 1 = 0. 5 P = 0. 5 CV 2 fck 1/fck p 1 = 0. 5 P = 0. 33 CV 2 fck p 1 = 0. 5 P = 0. 167 CV 2 fck Observe that the formula, Power, P = (1 – p 1) p 1 C V 2 fck = 0. 25 C V 2 fck is not correct. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 20

Switching Frequency Number of transitions per unit time: T = N(t) ─── t For a continuous signal: T = lim t→∞ N(t) ─── t T is defined as transition density. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 21

Static Signal Probabilities l Observe signal for interval t 0 + t 1 l Signal is 1 for duration t 1 l Signal is 0 for duration t 0 l Signal probabilities: l l p 1 = t 1/(t 0 + t 1) p 0 = t 0/(t 0 + t 1) = 1 – p 1 Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 22

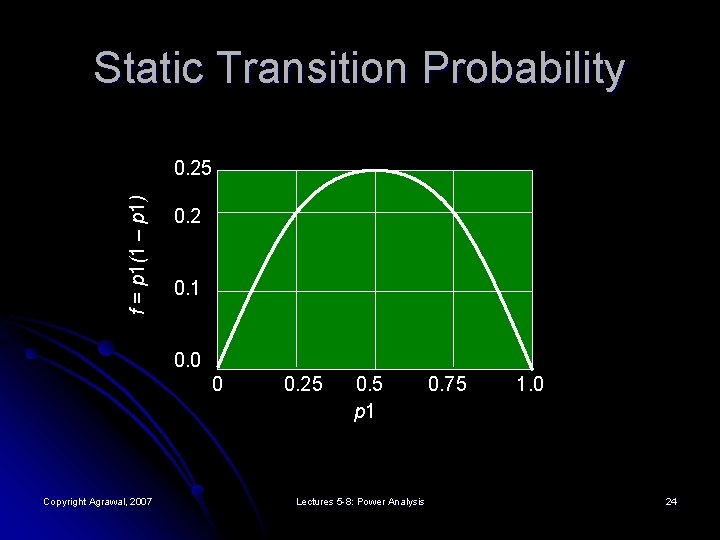
Static Transition Probabilities l Transition probabilities: l l l T 01 = p 0 Prob{signal is 1 | signal was 0} = p 0 p 1 T 10 = p 1 Prob{signal is 0 | signal was 1} = p 1 p 0 T = T 01 + T 10 = 2 p 0 p 1 = 2 p 1 (1 – p 1) Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 23

Static Transition Probability f = p 1(1 – p 1) 0. 25 0. 2 0. 1 0. 0 0 Copyright Agrawal, 2007 0. 25 0. 5 p 1 Lectures 5 -8: Power Analysis 0. 75 1. 0 24

Inaccuracy in Transition Probability p 1 = 0. 5 T = 1. 0 1/fck p 1 = 0. 5 T = 4/6 p 1 = 0. 5 T = 1/6 Observe that the formula, T = 2 p 1 (1 – p 1), is not correct. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 25

Cause for Error and Correction Probability of transition is not independent of the present state of the signal. l Determine probability p 01 of a 0→ 1 transition. l Recognize p 01 ≠ p 0 × p 1 l We obtain p 1 = (1 – p 1) p 01 + p 11 p 01 p 1 = ───── 1 – p 11 + p 01 l Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 26

Correction (Cont. ) Since p 11 + p 10 = 1, i. e. , given that the signal was previously 1, its present value can be either 1 or 0. l Therefore, p 01 p 1 = ────── p 10 + p 01 This uniquely gives signal probability as a function of transition probabilities. l Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 27

Transition and Signal Probabilities p 01 = p 10 = 1. 0 p 00 = p 11 = 0. 0 p 1 = 0. 5 1/fck p 01 = p 10 = 2/3 p 00 = p 11 = 1/3 p 1 = 0. 5 p 01 = p 10 = 1/4 p 00 = p 11 = 3/4 Copyright Agrawal, 2007 p 1 = 0. 5 Lectures 5 -8: Power Analysis 28

Probabilities: p 0, p 1, p 00, p 01, p 10, p 11 l l l p 01 + p 00 = 1 p 11 + p 10 = 1 p 0=1–p 1 p 01 p 1 = ─────── p 10 + p 01 Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 29

Transition Density l T = 2 p 1 (1 – p 1) = p 01 + p 10 = 2 p 10 p 01 / (p 10 + p 01) = 2 p 10 = 2 p 01 Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 30

Power Calculation Power can be estimated if transition density is known for all signals. l Calculation of transition density requires l l Signal probabilities l Transition densities for primary inputs; computed from vector statistics Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 31

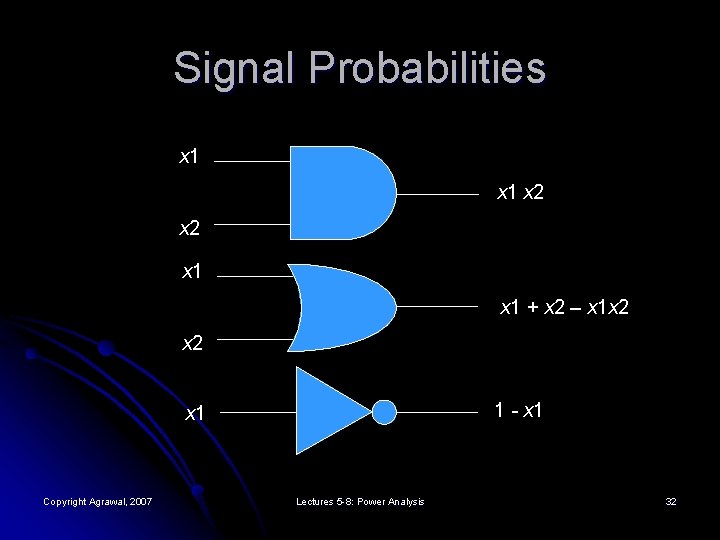
Signal Probabilities x 1 x 2 x 1 + x 2 – x 1 x 2 1 - x 1 Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 32

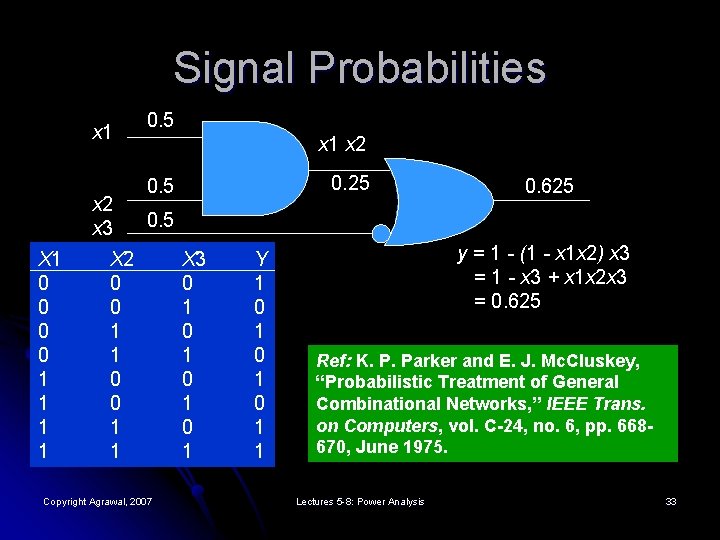
Signal Probabilities x 1 x 2 x 3 X 1 0 0 1 1 0. 5 x 1 x 2 0. 25 0. 625 0. 5 X 2 0 0 1 1 Copyright Agrawal, 2007 X 3 0 1 0 1 Y 1 0 1 0 1 1 y = 1 - (1 - x 1 x 2) x 3 = 1 - x 3 + x 1 x 2 x 3 = 0. 625 Ref: K. P. Parker and E. J. Mc. Cluskey, “Probabilistic Treatment of General Combinational Networks, ” IEEE Trans. on Computers, vol. C-24, no. 6, pp. 668670, June 1975. Lectures 5 -8: Power Analysis 33

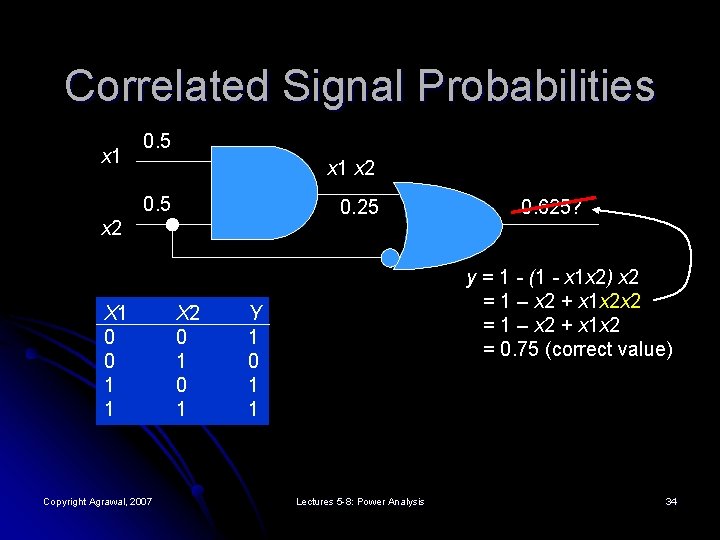
Correlated Signal Probabilities x 1 0. 5 x 1 x 2 0. 5 0. 25 x 2 X 1 0 0 1 1 Copyright Agrawal, 2007 X 2 0 1 0. 625? y = 1 - (1 - x 1 x 2) x 2 = 1 – x 2 + x 1 x 2 = 0. 75 (correct value) Y 1 0 1 1 Lectures 5 -8: Power Analysis 34

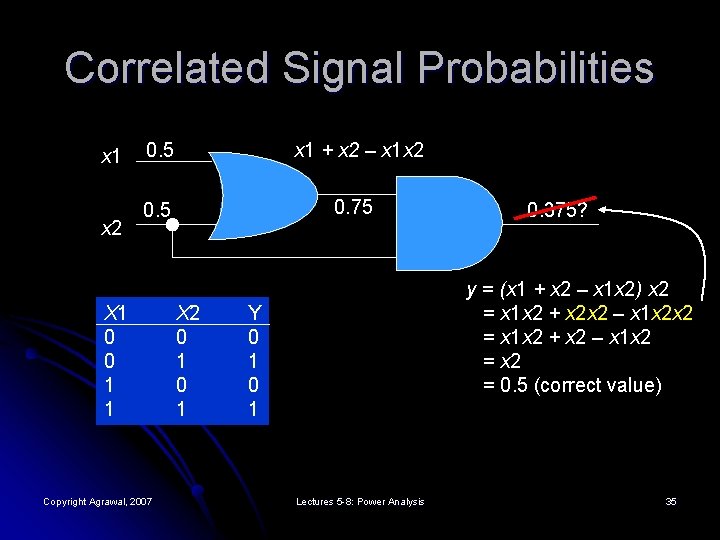
Correlated Signal Probabilities x 1 x 2 0. 5 x 1 + x 2 – x 1 x 2 0. 5 0. 75 X 1 0 0 1 1 Copyright Agrawal, 2007 X 2 0 1 0. 375? y = (x 1 + x 2 – x 1 x 2) x 2 = x 1 x 2 + x 2 x 2 – x 1 x 2 x 2 = x 1 x 2 + x 2 – x 1 x 2 = 0. 5 (correct value) Y 0 1 Lectures 5 -8: Power Analysis 35

Observation l Numerical computation of signal probabilities is accurate for fanout-free circuits. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 36

Remedies Use Shannon’s expansion theorem to compute signal probabilities. l Use Boolean difference formula to compute transition densities. l Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 37

Shannon’s Expansion Theorem l l C. E. Shannon, “A Symbolic Analysis of Relay and Switching Circuits, ” Trans. AIEE, vol. 57, pp. 713 -723, 1938. Consider: Boolean variables, X 1, X 2, . . . , Xn l Boolean function, F(X 1, X 2, . . . , Xn) l l l Then F = Xi F(Xi=1) + Xi’ F(Xi=0) Where Xi’ is complement of X 1 l Cofactors, F(Xi=j) = F(X 1, X 2, . . , Xi=j, . . , Xn), j = 0 or 1 l Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 38

Expansion About Two Inputs F = Xi. Xj F(Xi=1, Xj=1) + Xi. Xj’ F(Xi=1, Xj=0) + Xi’Xj F(Xi=0, Xj=1) + Xi’Xj’ F(Xi=0, Xj=0) l In general, a Boolean function can be expanded about any number of input variables. l Expansion about k variables will have 2 k terms. l Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 39

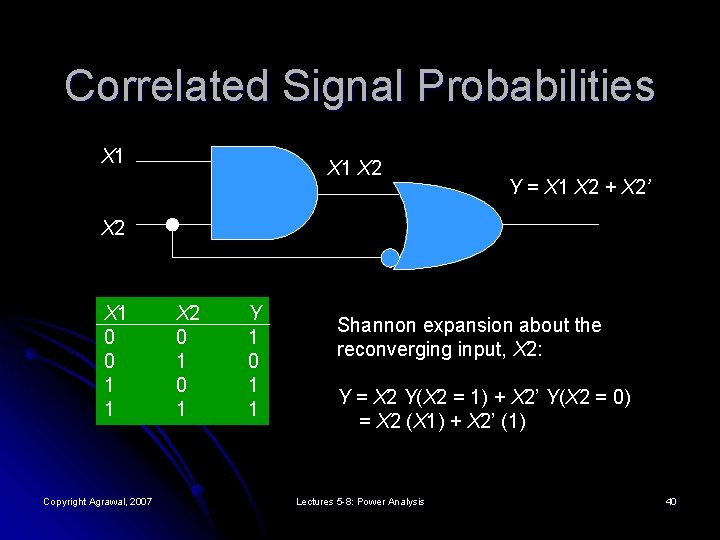
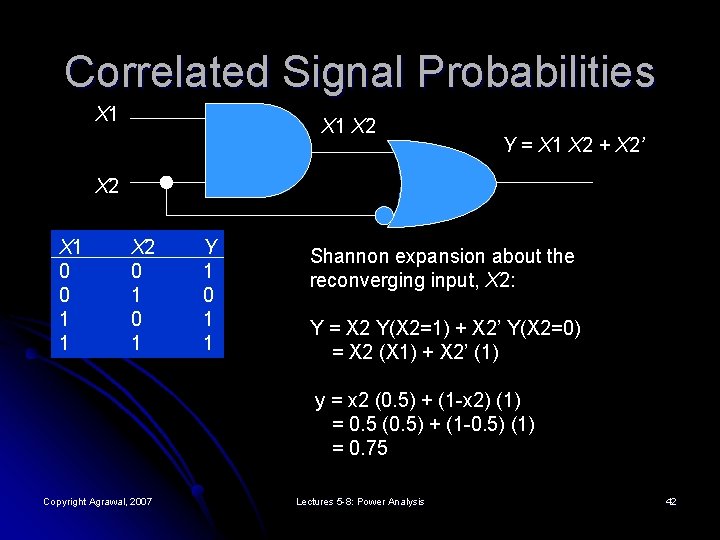
Correlated Signal Probabilities X 1 X 2 Y = X 1 X 2 + X 2’ X 2 X 1 0 0 1 1 Copyright Agrawal, 2007 X 2 0 1 Y 1 0 1 1 Shannon expansion about the reconverging input, X 2: Y = X 2 Y(X 2 = 1) + X 2’ Y(X 2 = 0) = X 2 (X 1) + X 2’ (1) Lectures 5 -8: Power Analysis 40

Correlated Signals l When the output function is expanded about all reconverging input variables, All cofactors correspond to fanout-free circuits. l Signal probabilities for cofactor outputs can be calculated without error. l A weighted sum of cofactor probabilities gives the correct probability of the output. l l For two reconverging inputs: f = xixj f(Xi=1, Xj=1) + xi(1 -xj) f(Xi=1, Xj=0) + (1 -xi)xj f(Xi=0, Xj=1) + (1 -xi)(1 -xj) f(Xi=0, Xj=0) Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 41

Correlated Signal Probabilities X 1 X 2 Y = X 1 X 2 + X 2’ X 2 X 1 0 0 1 1 X 2 0 1 Y 1 0 1 1 Shannon expansion about the reconverging input, X 2: Y = X 2 Y(X 2=1) + X 2’ Y(X 2=0) = X 2 (X 1) + X 2’ (1) y = x 2 (0. 5) + (1 -x 2) (1) = 0. 5 (0. 5) + (1 -0. 5) (1) = 0. 75 Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 42

Example 0. 5 1 0 0. 5 Reconv. signal Supergate 0. 25 0. 0 Point of reconv. 0. 0 0. 5 1. 0 0. 375 Signal probability for supergate output = 0. 5 Prob{rec. signal = 1} + 1. 0 Prob{rec. signal = 0} = 0. 5 × 0. 5 + 1. 0 × 0. 5 = 0. 75 S. C. Seth and V. D. Agrawal, “A New Model for Computation of Probabilistic Testability in Combinational Circuits, ” Integration, the VLSI Journal, vol. 7, no. 1, pp. 49 -75, April 1989. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 43

Probability Calculation Algorithm l Partition circuit into supergates. l l l Definition: A supergate is a circuit partition with a single output such that all fanouts that reconverge at the output are contained within the supergate. Identify reconverging and non-reconverging inputs of each supergate. Compute signal probabilities from PI to PO: l For a supergate whose input probabilities are known Enumerate reconverging input states l For each input state do gate by gate probability computation l Sum up corresponding signal probabilities, weighted by state probabilities l Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 44

Calculating Transition Density . . . x 1, T 1 xn, Tn Copyright Agrawal, 2007 1 Boolean function y, T(Y) = ? n Lectures 5 -8: Power Analysis 45

Boolean Difference Boolean diff(Y, Xi) = l ∂Y ── = Y(Xi=1) ⊕ Y(Xi=0) ∂Xi Boolean diff(Y, Xi) = 1 means that a path is sensitized from input Xi to output Y. l Prob(Boolean diff(Y, Xi) = 1) is the probability of transmitting a toggle from Xi to Y. l Probability of Boolean difference is determined from the probabilities of cofactors of Y with respect to Xi. F. F. Sellers, M. Y. Hsiao and L. W. Bearnson, “Analyzing Errors with the Boolean Difference, ” IEEE Trans. on Computers, vol. C-17, no. 7, pp. 676 -683, July 1968. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 46

Transition Density n T(y) = Σ T(Xi) Prob(Boolean diff(Y, Xi) = 1) i=1 F. Najm, “Transition Density: A New Measure of Activity in Digital Circuits, ” IEEE Trans. CAD, vol. 12, pp. 310 -323, Feb. 1993. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 47

Power Computation l l l For each primary input, determine signal probability and transition density for given vectors. For each internal node and primary output Y, find the transition density T(Y), using supergate partitioning and the Boolean difference formula. Compute power, P= Σ 0. 5 CY V 2 T(Y) all Y where CY is the capacitance of node Y and V is supply voltage. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 48

Transition Density and Power X 1 X 2 X 3 0. 2, 1 0. 3, 2 0. 06, 0. 7 0. 436, 3. 24 Ci Y 0. 4, 3 CY Transition density Signal probability Power = 0. 5 V 2 (0. 7 Ci + 3. 24 CY) Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 49

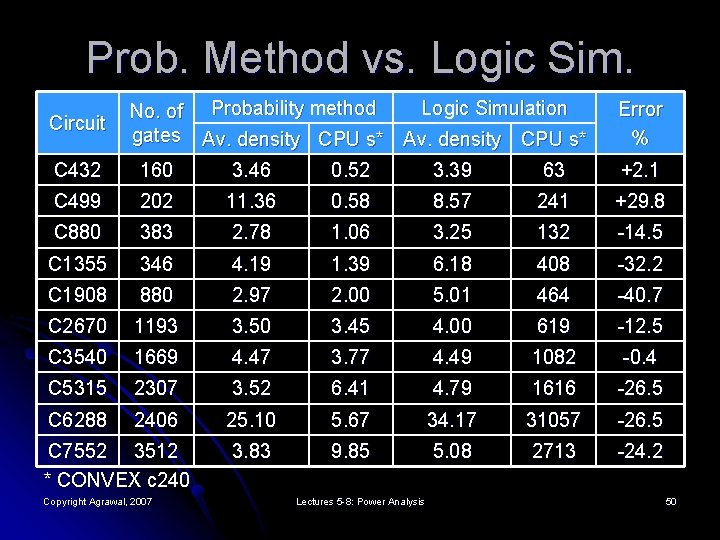
Prob. Method vs. Logic Sim. Circuit Logic Simulation No. of Probability method gates Av. density CPU s* Error % C 432 160 3. 46 0. 52 3. 39 63 +2. 1 C 499 202 11. 36 0. 58 8. 57 241 +29. 8 C 880 383 2. 78 1. 06 3. 25 132 -14. 5 C 1355 346 4. 19 1. 39 6. 18 408 -32. 2 C 1908 880 2. 97 2. 00 5. 01 464 -40. 7 C 2670 1193 3. 50 3. 45 4. 00 619 -12. 5 C 3540 1669 4. 47 3. 77 4. 49 1082 -0. 4 C 5315 2307 3. 52 6. 41 4. 79 1616 -26. 5 C 6288 2406 25. 10 5. 67 34. 17 31057 -26. 5 3. 83 9. 85 5. 08 2713 -24. 2 C 7552 3512 * CONVEX c 240 Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 50

Probability Waveform Methods l l F. Najm, R. Burch, P. Yang and I. Hajj, “CREST – A Current Estimator for CMOS Circuits, ” Proc. IEEE Int. Conf. on CAD, Nov. 1988, pp. 204 -207. C. -S. Ding, et al. , “Gate-Level Power Estimation using Tagged Probabilistic Simulation, ” IEEE Trans. on CAD, vol. 17, no. 11, pp. 1099 -1107, Nov. 1998. F. Hu and V. D. Agrawal, “Dual-Transition Glitch Filtering in Probabilistic Waveform Power Estimation, ” Proc. IEEE Great Lakes Symp. VLSI, Apr. 2005, pp. 357 -360. F. Hu and V. D. Agrawal, “Enhanced Dual-Transition Probabilistic Power Estimation with Selective Supergate Analysis, ” Proc. IEEE Int. Conf. Computer Design, Oct. 2005. pp. 366 -369. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 51

Problem 1 For equiprobable inputs analyze the 0→ 1 transition probabilities of all gates in the two implementations of a four-input AND gate shown below. Assuming that the gates have zero delays, which implementation will consume less average dynamic power? E A B C D F G A B C D G F Tree structure Chain structure Copyright Agrawal, 2007 E Lectures 5 -8: Power Analysis 52

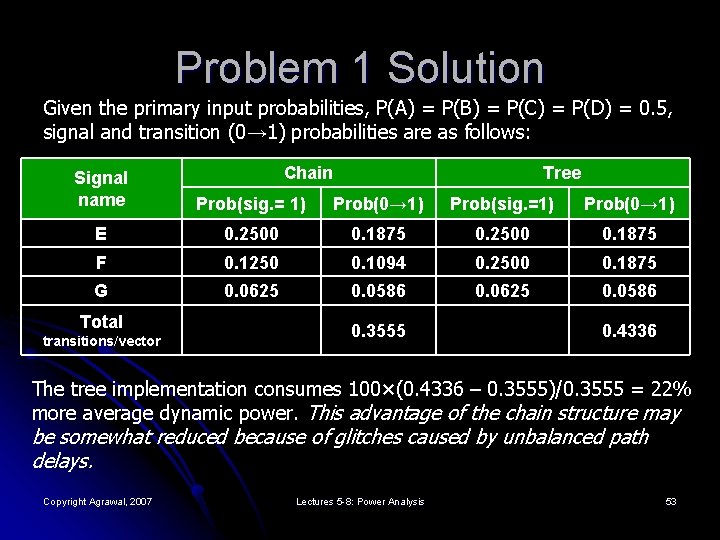
Problem 1 Solution Given the primary input probabilities, P(A) = P(B) = P(C) = P(D) = 0. 5, signal and transition (0→ 1) probabilities are as follows: Chain Tree Signal name Prob(sig. = 1) Prob(0→ 1) Prob(sig. =1) Prob(0→ 1) E 0. 2500 0. 1875 F 0. 1250 0. 1094 0. 2500 0. 1875 G 0. 0625 0. 0586 Total transitions/vector 0. 3555 0. 4336 The tree implementation consumes 100×(0. 4336 – 0. 3555)/0. 3555 = 22% more average dynamic power. This advantage of the chain structure may be somewhat reduced because of glitches caused by unbalanced path delays. Copyright Agrawal, 2007 Lectures 5 -8: Power Analysis 53

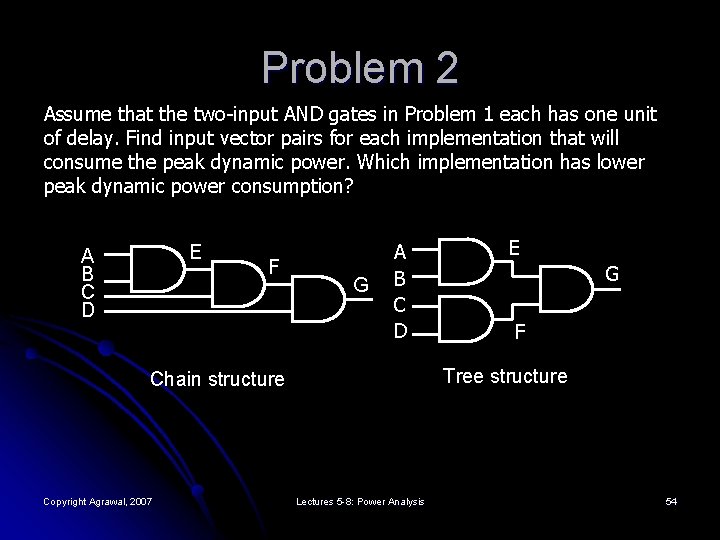
Problem 2 Assume that the two-input AND gates in Problem 1 each has one unit of delay. Find input vector pairs for each implementation that will consume the peak dynamic power. Which implementation has lower peak dynamic power consumption? E A B C D F G A B C D G F Tree structure Chain structure Copyright Agrawal, 2007 E Lectures 5 -8: Power Analysis 54

Problem 2 Solution For the chain structure, a vector pair {A B C D} = {1110}, {1011} will produce four gate transitions as shown below. A E F B C D G A=11 B=10 E=10 C=11 F=10 D=01 G=00 0 Copyright Agrawal, 2007 1 2 3 Lectures 5 -8: Power Analysis Time units 55

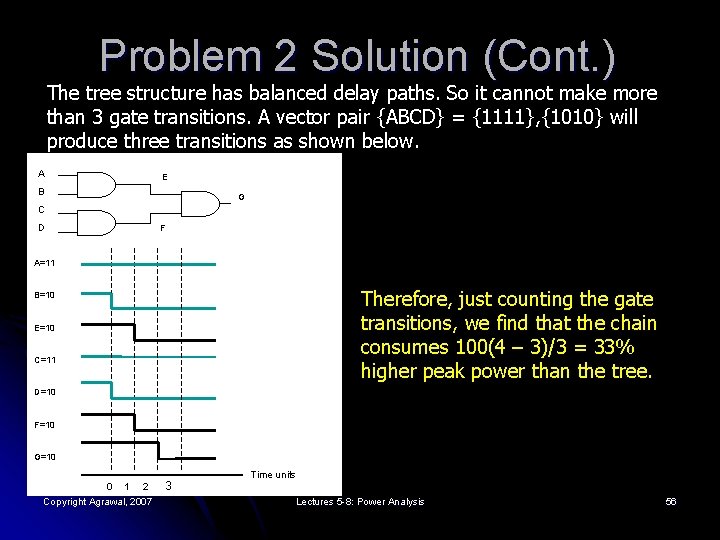
Problem 2 Solution (Cont. ) The tree structure has balanced delay paths. So it cannot make more than 3 gate transitions. A vector pair {ABCD} = {1111}, {1010} will produce three transitions as shown below. A E B G C D F A=11 Therefore, just counting the gate transitions, we find that the chain consumes 100(4 – 3)/3 = 33% higher peak power than the tree. B=10 E=10 C=11 D=10 F=10 G=10 0 1 2 Copyright Agrawal, 2007 3 Time units Lectures 5 -8: Power Analysis 56