Digital Logic Design GateLevel Minimization 4 Introduction Gatelevel

Digital Logic Design Gate-Level Minimization 4

Introduction Gate-level minimization refers to the design task of finding an optimal gate-level implementation of Boolean functions describing a digital circuit. 5

Introduction of K-Map (Karnaugh Map) In many digital circuits and practical problems we need to find expression with minimum variables. We can minimize Boolean expressions of 3, 4 variables very easily using K-map without using any Boolean algebra theorems. 6

K-map can take two forms Sum of Product (SOP) and Product of Sum (POS) according to the need of problem. K-map is table like representation but it gives more information than TRUTH TABLE. We fill grid of K-map with 0’s and 1’s then solve it by making groups. March 3, 2021 7

Steps to solve expression using K-map 1. Select K-map according to the number of variables. 2. Identify minterms or maxterms as given in problem. 3. For SOP put 1’s in blocks of K-map respective to the minterms (0’s elsewhere). 4. For POS put 0’s in blocks of K-map respective to the maxterms(1’s elsewhere). 5. Make rectangular groups containing total terms in power of two like 2, 4, 8. . (except 1) and try to cover as many elements as you can in one group. 6. From the groups made in step 5 find the product terms and sum them up for SOP form. 8

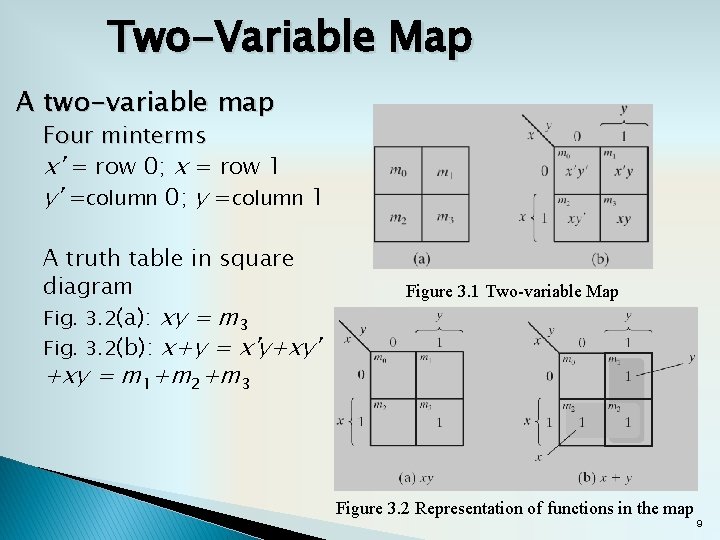
Two-Variable Map A two-variable map Four minterms x' = row 0; x = row 1 y' =column 0; y =column 1 A truth table in square diagram Fig. 3. 2(a): xy = m 3 Fig. 3. 2(b): x+y = x'y+xy' Figure 3. 1 Two-variable Map +xy = m 1+m 2+m 3 Figure 3. 2 Representation of functions in the map 9

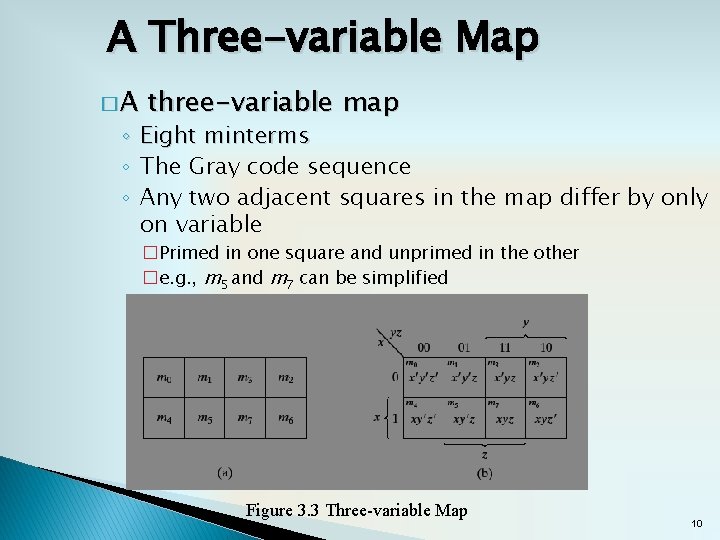
A Three-variable Map �A ◦ ◦ ◦ three-variable map Eight minterms The Gray code sequence Any two adjacent squares in the map differ by only on variable �Primed in one square and unprimed in the other �e. g. , m 5 and m 7 can be simplified �m 5+ m 7 = xy'z + xyz = xz (y'+y) = xz Figure 3. 3 Three-variable Map 10

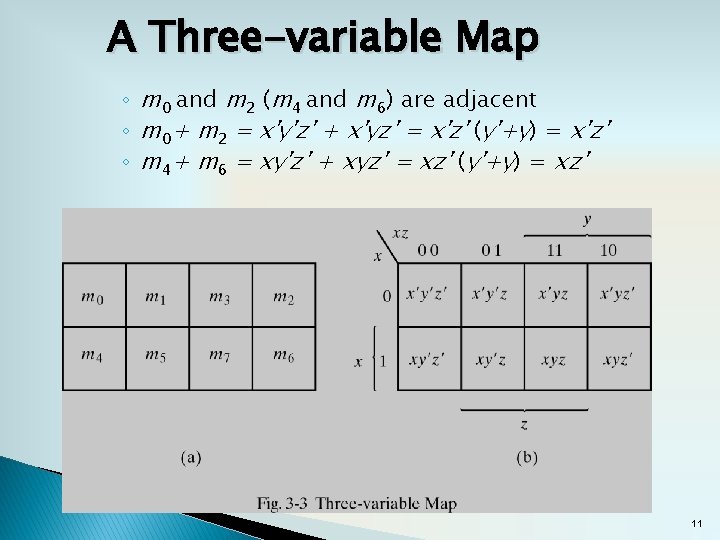
A Three-variable Map ◦ m 0 and m 2 (m 4 and m 6) are adjacent ◦ m 0+ m 2 = x'y'z' + x'yz' = x'z' (y'+y) = x'z' ◦ m 4+ m 6 = xy'z' + xyz' = xz' (y'+y) = xz' 11

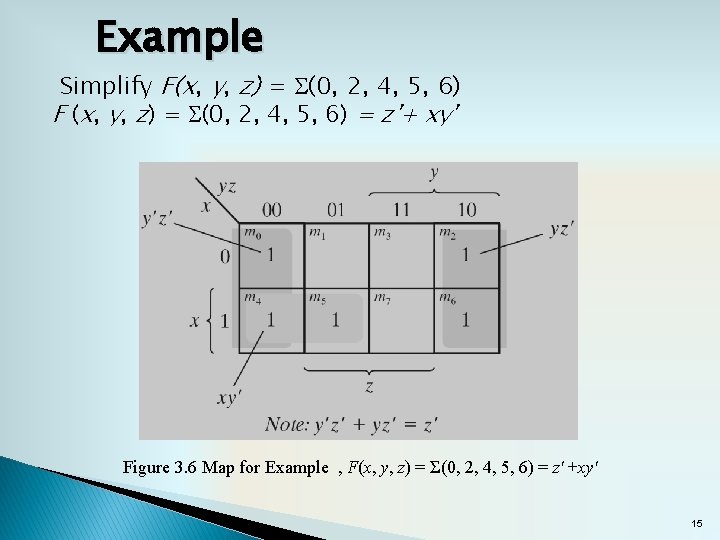
Example � simplify the Boolean function F(x, y, z) = S(2, 3, 4, 5) ◦ F(x, y, z) = S(2, 3, 4, 5) = x'y + xy' Figure 3. 4 Map for Example , F(x, y, z) = Σ(2, 3, 4, 5) = x'y + xy' 12

Example � simplify F(x, y, z) = S(3, 4, 6, 7) ◦ F(x, y, z) = S(3, 4, 6, 7) = yz+ xz' Figure 3. 5 Map for Example ; F(x, y, z) = Σ(3, 4, 6, 7) = yz + xz' 13

Four adjacent Squares � Consider four adjacent squares ◦ 2, 4, and 8 squares ◦ m 0+m 2+m 4+m 6 = x'y'z'+x'yz'+xy'z'+xyz' = x'z'(y'+y) +xz'(y'+y) = x'z' + xz‘ = z' ◦ m 1+m 3+m 5+m 7 = x'y'z+x'yz+xy'z+xyz =x'z(y'+y) + xz(y'+y) =x'z + xz = z Three-variable Map 14

Example Simplify F(x, y, z) = S(0, 2, 4, 5, 6) F (x, y, z) = S(0, 2, 4, 5, 6) = z'+ xy' Figure 3. 6 Map for Example , F(x, y, z) = Σ(0, 2, 4, 5, 6) = z' +xy' 15

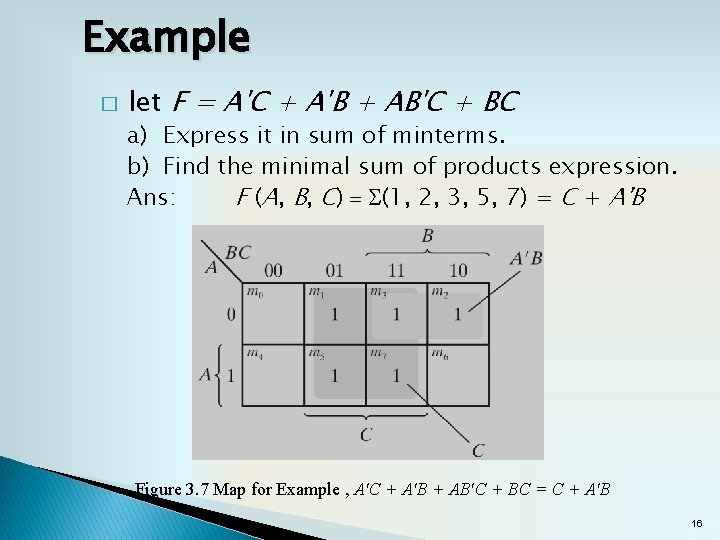
Example � let F = A'C + A'B + AB'C + BC a) Express it in sum of minterms. b) Find the minimal sum of products expression. Ans: F (A, B, C) = S(1, 2, 3, 5, 7) = C + A'B Figure 3. 7 Map for Example , A'C + A'B + AB'C + BC = C + A'B 16

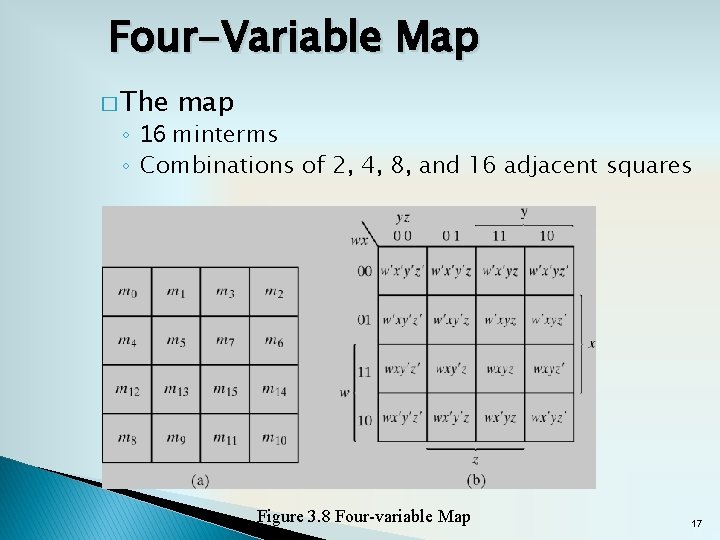
Four-Variable Map � The map ◦ 16 minterms ◦ Combinations of 2, 4, 8, and 16 adjacent squares Figure 3. 8 Four-variable Map 17

Example Simplify F (w, x, y, z) = S(0, 1, 2, 4, 5, 6, 8, 9, 12, 13, 14) F = y'+w'z'+xz' Figure 3. 9 Map F(w, x, y, z) = Σ(0, 1, 2, 4, 5, 6, 8, 9, 12, 13, 14) = y' + w' z' +xz' 18

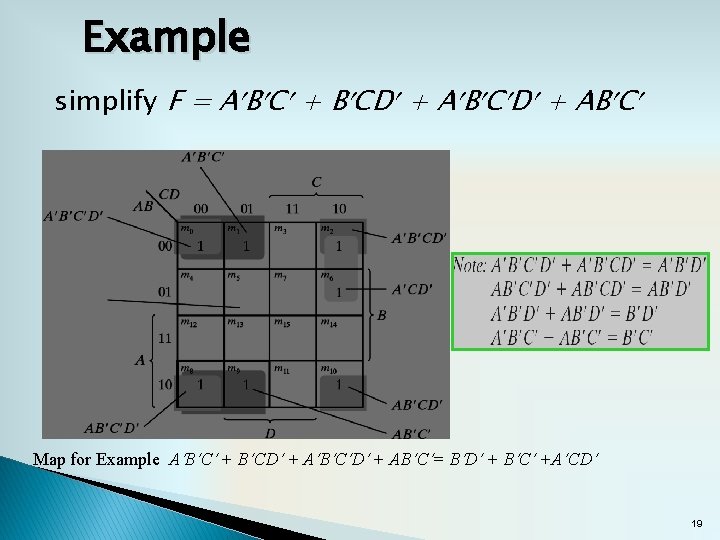
Example simplify F = A B C + B CD + A B C D + AB C Map for Example A B C + B CD + A B C D + AB C = B D + B C +A CD 19

Prime Implicants � Consider F(A, B, C, D) = Σ(0, 2, 3, 5, 7, 8, 9, 10, 11, 13, 15) ◦ The simplified expression may not be unique ◦ F = BD+B'D'+CD+AD = BD+B'D'+CD+AB' = BD+B'D'+B'C+AD = BD+B'D'+B'C+AB' 20

Product of Sums Simplification � Approach #1 � Approach #2: duality ◦ Simplified F' in the form of sum of products ◦ Apply De. Morgan's theorem F = (F‘ )' ◦ F‘ : sum of products → F: product of sums ◦ Combinations of maxterms (it was minterms) ◦ M 0 M 1 = (A+B+C+D)(A+B+C+D') = (A+B+C)+(DD‘ ) = CD A+B+C AB 00 01 11 10 00 M 1 M 3 M 2 M 13 M 15 M 14 01 11 10 M 4 M 8 M 5 M 9 M 7 M 11 M 6 M 10 21

Example simplify F = S(0, 1, 2, 5, 8, 9, 10) into (a) sum-of-products form, and (b) product-of-sums form: a) F(A, B, C, D)= S(0, 1, 2, 5, 8, 9, 10) = B'D'+B'C'+A'C'D b) F' = AB+CD+BD' Apply De. Morgan's theorem; F=(A'+B')(C'+D')(B'+D) » Or think in terms of maxterms » Figure Map for Example F(A, B, C, D)= S(0, 1, 2, 5, 8, 9, 10) = B'D'+B'C'+A'C'D 22

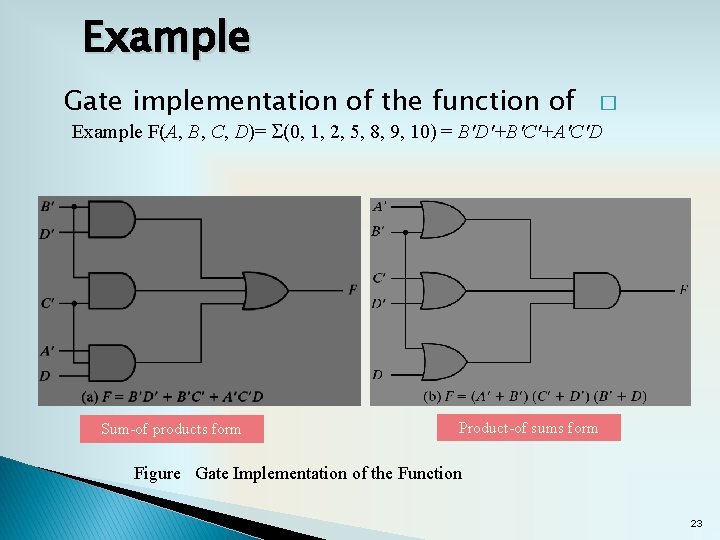
Example Gate implementation of the function of � Example F(A, B, C, D)= S(0, 1, 2, 5, 8, 9, 10) = B'D'+B'C'+A'C'D Sum-of products form Product-of sums form Figure Gate Implementation of the Function 23

Sum-of-Minterm Procedure Consider the function defined in Table � In sum-of-minterm: ◦ In sum-of-maxterm � Taking the complement of F ◦ 24

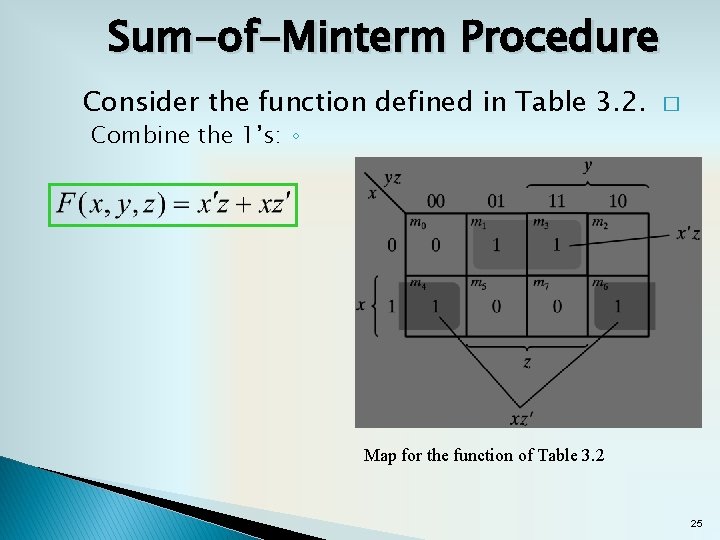
Sum-of-Minterm Procedure Consider the function defined in Table 3. 2. � Combine the 1’s: ◦ Combine the 0’s : ◦ Map for the function of Table 3. 2 25

26