CICLO TRIGONOMTRICO PROFESSORA TELMA CASTRO SILVA Medidas de

CICLO TRIGONOMÉTRICO PROFESSORA TELMA CASTRO SILVA

Medidas de Arcos As unidades mais usadas são o grau (°) e o radiano (rad). Grau: é quando dividimos uma circunferência em 360 partes congruentes, sendo cada uma dessas partes correspondentes a um arco de um grau (1 o).

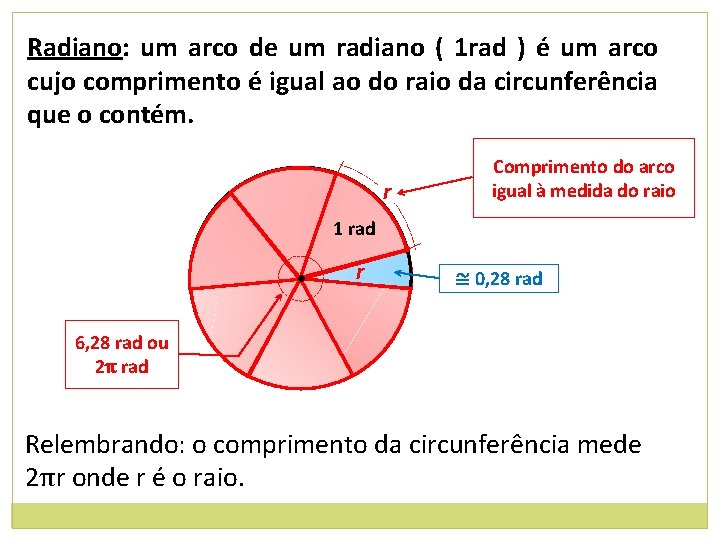
Radiano: um arco de um radiano ( 1 rad ) é um arco cujo comprimento é igual ao do raio da circunferência que o contém. Comprimento do arco igual à medida do raio r 1 rad • r • ≅ 0, 28 rad 6, 28 rad ou 2π rad Relembrando: o comprimento da circunferência mede 2πr onde r é o raio.

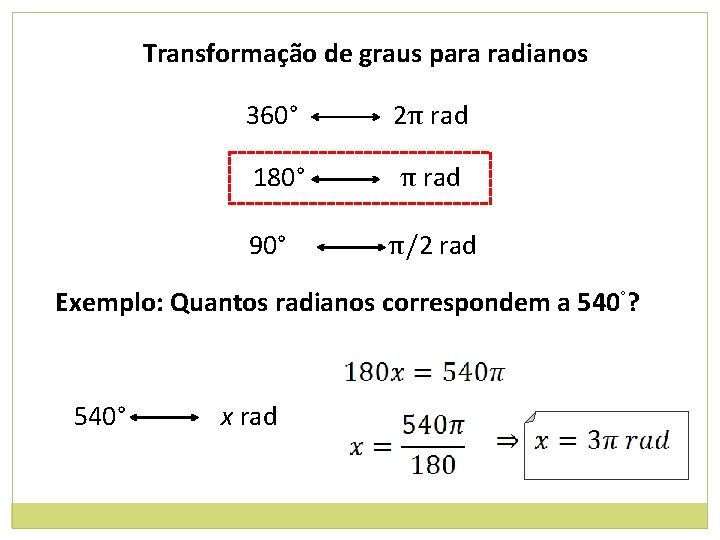
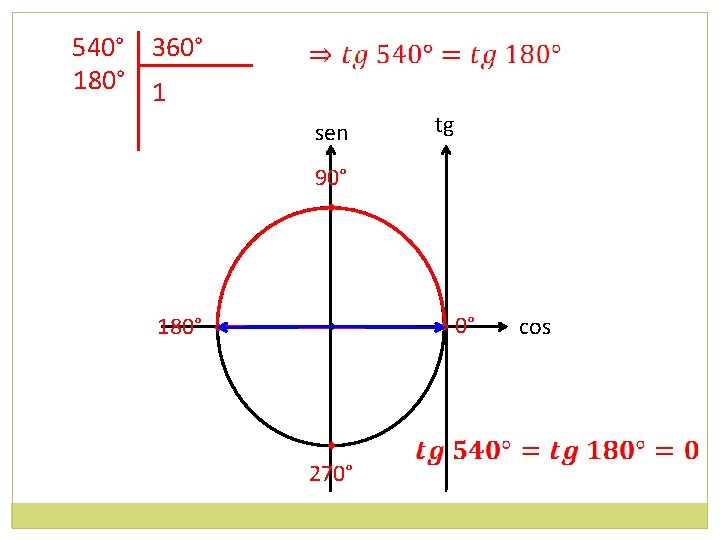
Transformação de graus para radianos 360° 2π rad 180° π rad 90° π/2 rad Exemplo: Quantos radianos correspondem a 540°? 540° x rad

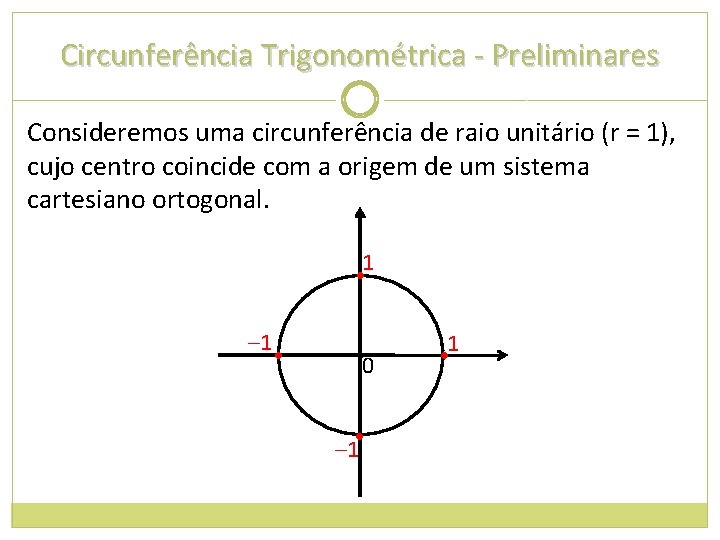
Circunferência Trigonométrica - Preliminares Consideremos uma circunferência de raio unitário (r = 1), cujo centro coincide com a origem de um sistema cartesiano ortogonal. 1 • – 1 • • 0 • – 1 • 1

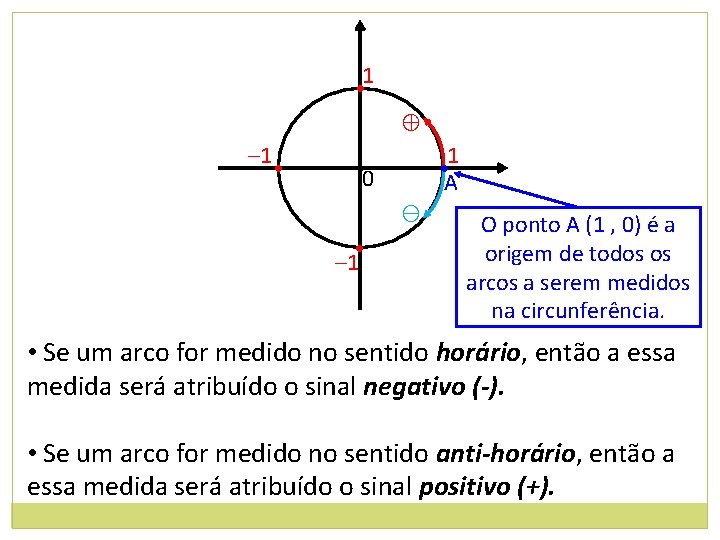
1 • ⊕ – 1 • • 1 A • 0 ⊖ • – 1 O ponto A (1 , 0) é a origem de todos os arcos a serem medidos na circunferência. • Se um arco for medido no sentido horário, então a essa medida será atribuído o sinal negativo (-). • Se um arco for medido no sentido anti-horário, então a essa medida será atribuído o sinal positivo (+).

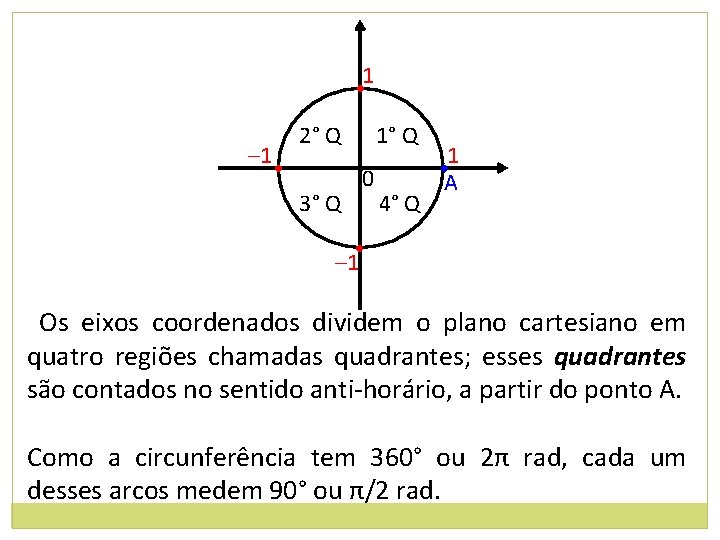
1 • – 1 • 2° Q 3° Q 1° Q • 0 4° Q • 1 A • – 1 Os eixos coordenados dividem o plano cartesiano em quatro regiões chamadas quadrantes; esses quadrantes são contados no sentido anti-horário, a partir do ponto A. Como a circunferência tem 360° ou 2π rad, cada um desses arcos medem 90° ou π/2 rad.

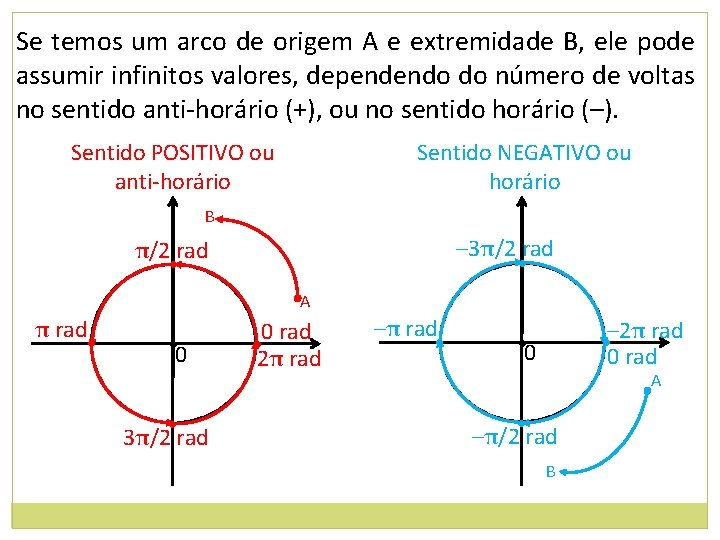
Se temos um arco de origem A e extremidade B, ele pode assumir infinitos valores, dependendo do número de voltas no sentido anti-horário (+), ou no sentido horário (–). Sentido POSITIVO ou anti-horário Sentido NEGATIVO ou horário B – 3π/2 rad • A π rad • • 0 • 3π/2 rad • 0 rad 2π rad –π rad • • – 2π rad 0 rad • 0 A • –π/2 rad B

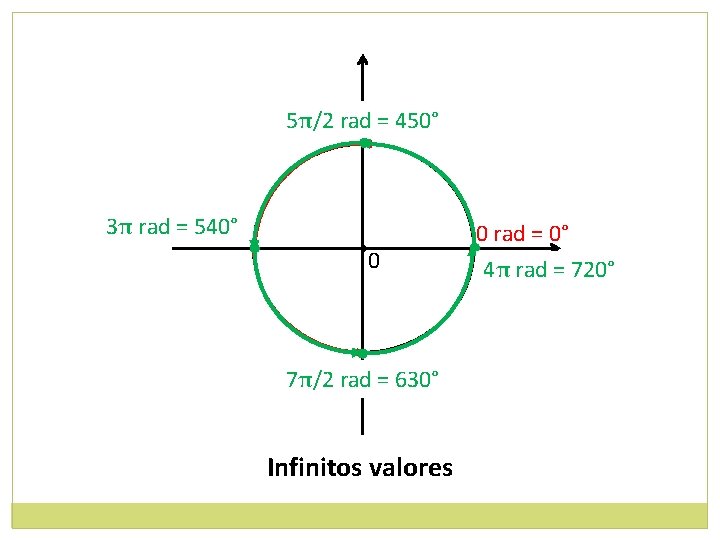
5π/2 rad==90° 450° π/2 rad • 3ππrad rad==540° 180° • • 0 • 3π/2 7π/2 rad rad==270° 630° Infinitos valores • 0 rad = 0° 2π 4πrad rad==360° 720°

Exercícios ARCOS E NGULOS

1. Expresse em graus: a) b) c) d) e)

Solução: Esse cálculo também poderia ser realizado pela regra de três, mas outra forma é substituir π rad pelo seu correspondente em graus, 180º, e simplificar a fração. 20 a) 1 b) 45 clicar 2

Solução: Esse cálculo também poderia ser realizado pela regra de três, mas outra forma é substituir π rad pelo seu correspondente em graus, 180º, e simplificar a fração. 20 a) 1 45 b) 20 9 2 d) c) 1 60 e) 1 1

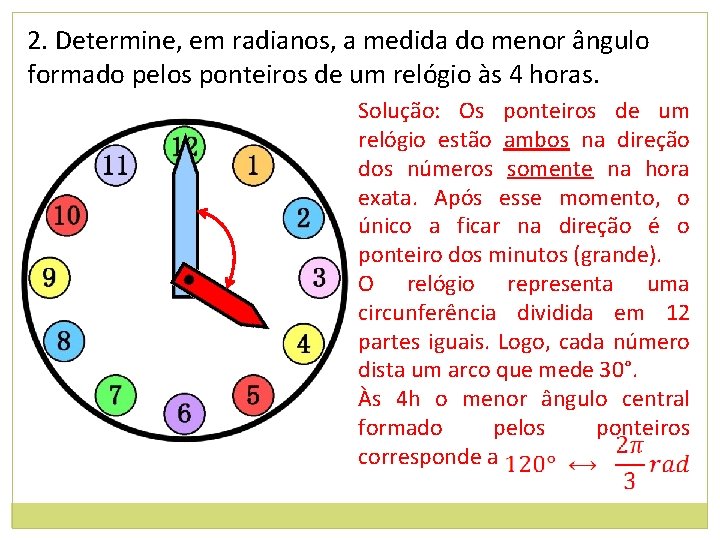
2. Determine, em radianos, a medida do menor ângulo formado pelos ponteiros de um relógio às 4 horas. Solução: Os ponteiros de um relógio estão ambos na direção dos números somente na hora exata. Após esse momento, o único a ficar na direção é o ponteiro dos minutos (grande). O relógio representa uma circunferência dividida em 12 partes iguais. Logo, cada número dista um arco que mede 30°. Às 4 h o menor ângulo central formado pelos ponteiros corresponde a

3. Se o ponteiro menor de um relógio percorre um arco de ( π/12) radianos, que arco ponteiro maior percorre? Solução: Em graus a medida percorrida pelo menor corresponde a 15°. Esse valor corresponde à metade da distância entre dois números consecutivos. O tempo para percorrer essa distância pelo menor é de meia hora. Enquanto isso o ponteiro maior dá meia volta completa, isto é, 180°. Logo, o ponteiro maior percorre π rad.

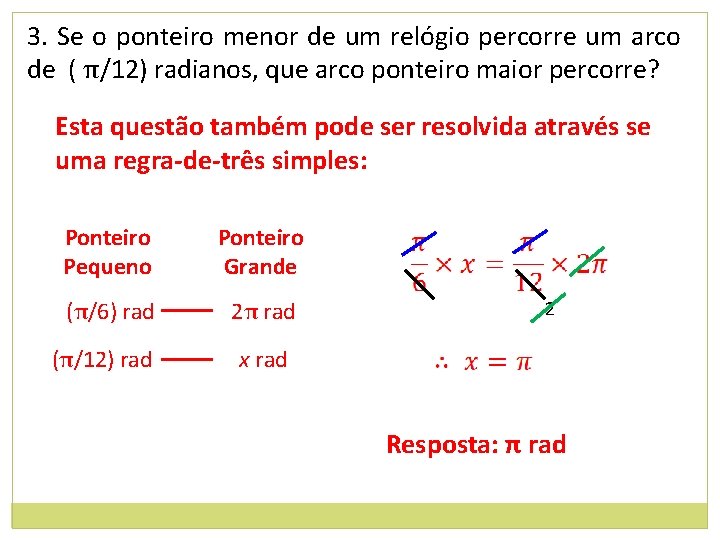
3. Se o ponteiro menor de um relógio percorre um arco de ( π/12) radianos, que arco ponteiro maior percorre? Esta questão também pode ser resolvida através se uma regra-de-três simples: Ponteiro Pequeno Ponteiro Grande (π/6) rad 2π rad (π/12) rad 2 x rad Resposta: π rad

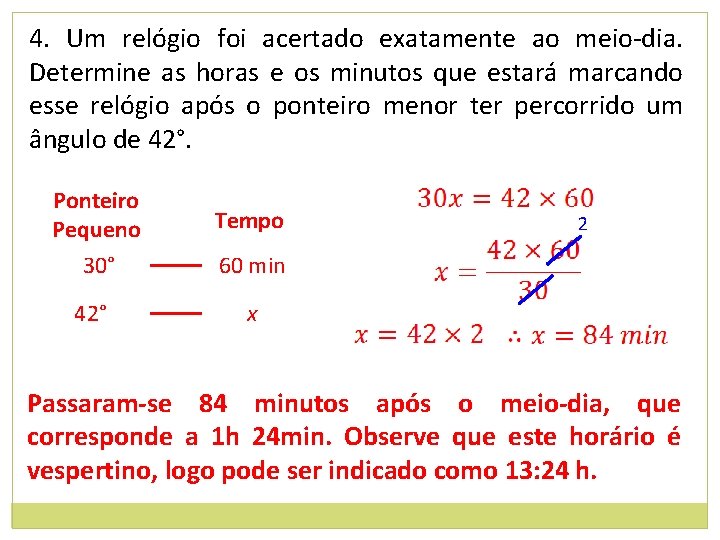
4. Um relógio foi acertado exatamente ao meio-dia. Determine as horas e os minutos que estará marcando esse relógio após o ponteiro menor ter percorrido um ângulo de 42°. Ponteiro Pequeno Tempo 30° 60 min 42° 2 x Passaram-se 84 minutos após o meio-dia, que corresponde a 1 h 24 min. Observe que este horário é vespertino, logo pode ser indicado como 13: 24 h.

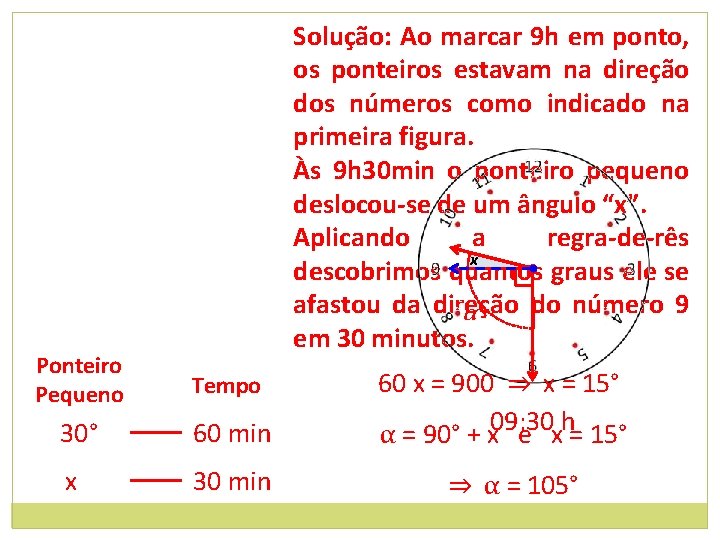
5. Qual a medida, em graus, do menor ângulo central formado pelos ponteiros de um relógio que está marcando 9 h 30 min? x α 09: 00 h 09: 30 h

Solução: Ao marcar 9 h em ponto, os ponteiros estavam na direção dos números como indicado na primeira figura. Às 9 h 30 min o ponteiro pequeno deslocou-se de um ângulo “x”. Aplicando a regra-de-rês x descobrimos quantos graus ele se afastou da direção do número 9 α em 30 minutos. Ponteiro Pequeno Tempo 30° 60 min x 30 min 60 x = 900 ⇒ x = 15° α = 90° + x 09: 30 e xh= 15° ⇒ α = 105°

6. Determine: a) o comprimento de um arco de circunferência (em cm), sabendo que ela tem 12 cm de raio e o ângulo central correspondente mede 20°. b) o ângulo central (em radianos) correspondente a um arco de 15 cm de comprimento, sabendo que ela tem raio de 20 cm. c) a medida do raio de uma circunferência (em cm), sabendo que nela um ângulo central de 15° corresponde a um arco de 30 cm.

a) o comprimento de um arco de circunferência (em cm), sabendo que ela tem 12 cm de raio e o ângulo central correspondente mede 20°. ⇒

b) o ângulo central (em radianos) correspondente a um arco de 15 cm de comprimento, sabendo que ela tem raio de 20 cm. ⇒

c) a medida do raio de uma circunferência (em cm), sabendo que nela um ângulo central de 15° corresponde a um arco de 30 cm. ⇒

7. A roda dianteira de uma bicicleta tem 40 cm de raio. Quantos metros ela percorre ao dar 5. 000 voltas? Quantas voltas ela deve dar para percorrer 9420 m? 40 cm = 0, 4 m ⇒ C = 2π × 0, 4 m ∴ C ≅ 2, 5 m 1 volta = 2, 5 m ⇒ 5000 voltas = 5000 × 2, 5 m = 12. 500 m 1 volta = 2, 5 m ⇒ x voltas = 2, 5 x = 9. 420 m

8. As rodas de um automóvel têm 70 cm de diâmetro. Determine o número de voltas efetuadas pelas rodas quando o automóvel percorre 9. 891 km. Adote π = 3, 14. d = 70 cm ∴ r = 35 cm 1 volta = C = 2π × 35 = 70π cm = 219, 8 cm = 2, 198 m Percurso = 9. 891 km = 9. 891. 000 m x voltas = 2, 198. x = 9891000 ∴ x = 4. 500. 000 voltas

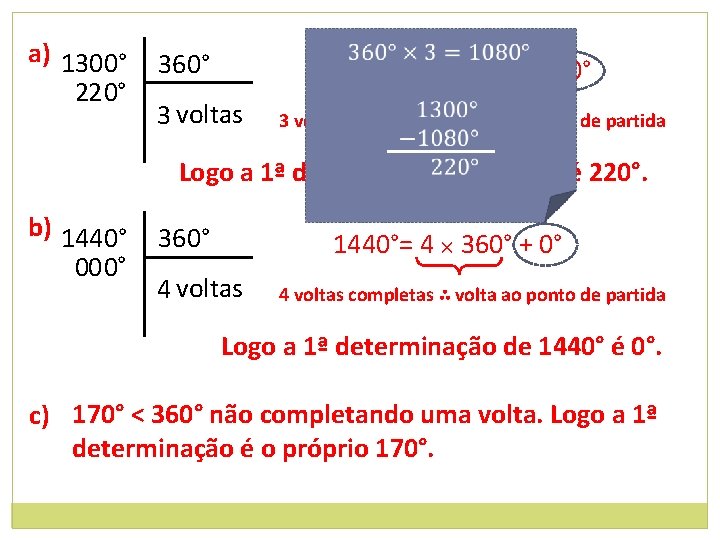
9. Obtenha as menores determinações não negativas dos arcos. a) 1300° b) 1440° c) 170° d) Solução: Encontra-se o número de voltas completas que é múltiplo de 360° ou de 2π. As menores determinações não negativas serão os arcos encontrados nos restos e) percorridos no sentido positivo. f) – 1200° São chamadas 1ªs determinações.

a) 1300° 22 0° 360° 1300°= 3 × 360° + 220° 3 voltas completas ∴ volta ao ponto de partida Logo a 1ª determinação de 1300° é 220°. b) 1440° 00 0° 360° 1440°= 4 × 360° + 0° 4 voltas completas ∴ volta ao ponto de partida Logo a 1ª determinação de 1440° é 0°. c) 170° < 360° não completando uma volta. Logo a 1ª determinação é o próprio 170°.

d) Vamos dividir o arco por 2π rad Sabemos que: mais ¾ de volta. ou seja, 2 voltas ¾ de uma volta, em radianos, serão: 1 2

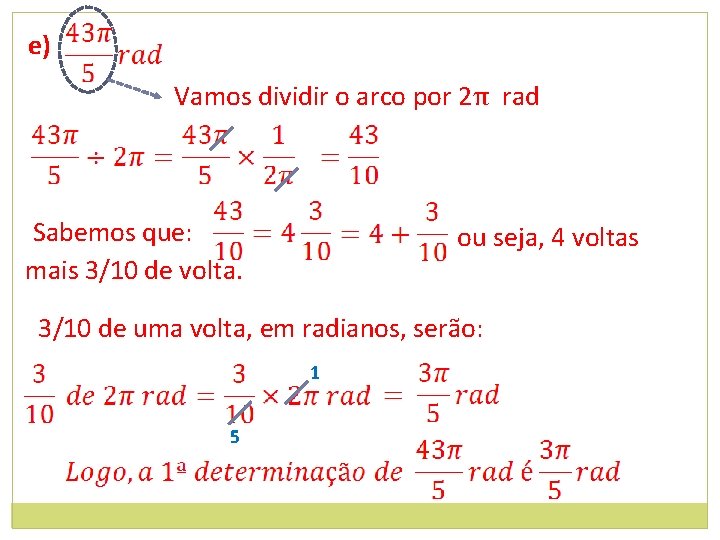
e) Vamos dividir o arco por 2π rad Sabemos que: mais 3/10 de volta. ou seja, 4 voltas 3/10 de uma volta, em radianos, serão: 1 5

f) – 1200° – 1 2 0° 360° – 3 voltas – 1300°= – 3 × 360° – 120° 3 voltas completas no sentido horário (negativo) ∴ volta ao ponto de partida – 120° é a 1ª determinação negativa de – 1200°. Para encontrar a 1ª determinação positiva, devemos somar 360° a – 120° + 360° = 240° Logo a 1ª determinação negativa de – 1200° é 240° (sentido positivo).

Visualização de determinações positiva e negativa: 90° • • 0° 180° • +240° ≡ – 120° • • 270°

10. Dê as expressões gerais dos arcos côngruos a: a) 1700° Solução: A expressão geral será b) – 700° dada pela 1ª determinação dos c) ângulos adicionadas a múltiplos de d) e) 360° ou 2π, positivos ou negativos.

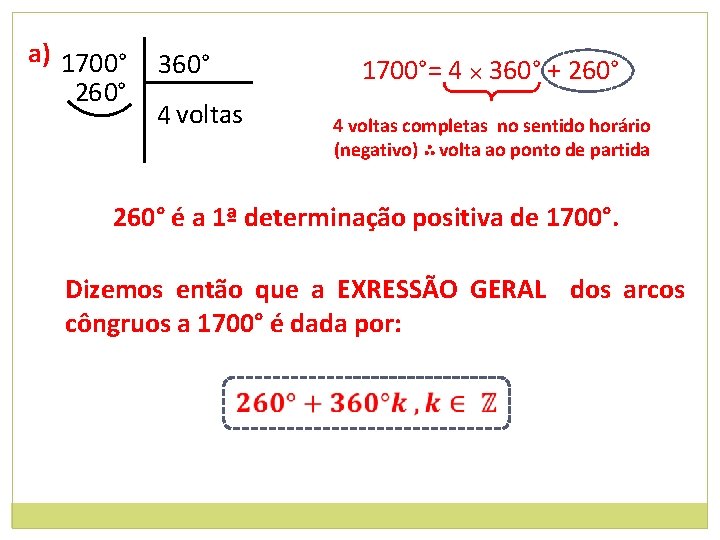
a) 1700° 26 0° 360° 4 voltas 1700°= 4 × 360° + 260° 4 voltas completas no sentido horário (negativo) ∴ volta ao ponto de partida 260° é a 1ª determinação positiva de 1700°. Dizemos então que a EXRESSÃO GERAL dos arcos côngruos a 1700° é dada por:

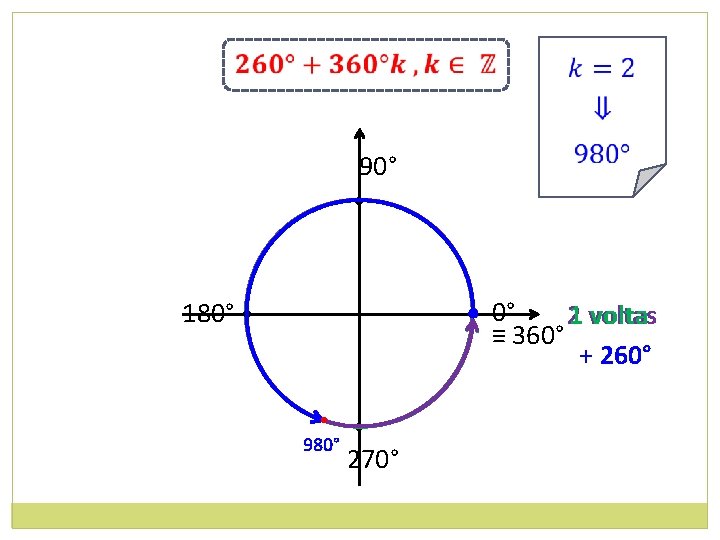
a) 1700° 26 0° 360° 4 voltas Sendo k um número inteiro, ao escrevermos 360°k, queremos expressar um número qualquer de voltas completas em qualquer sentido – positivo ou negativo. Ao somarmos 260°, dizemos que, depois de voltar ao ponto de partida – não importando quantas voltas foram dadas antes – percorremos mais 260° e chegamos sempre ao mesmo ponto.

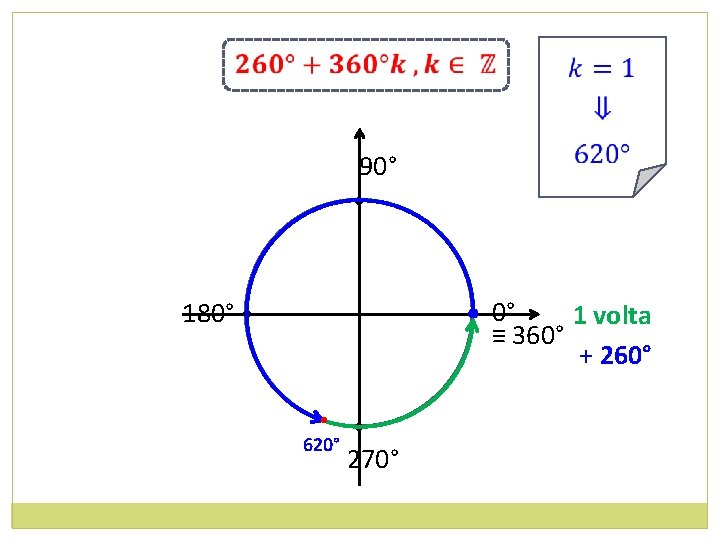
90° • • 0° 1 volta ≡ 360° + 260° 180° • • 620° • 270°

90° • • 0° volta 21 voltas ≡ 360° + 260° 180° • • 980° • 270°

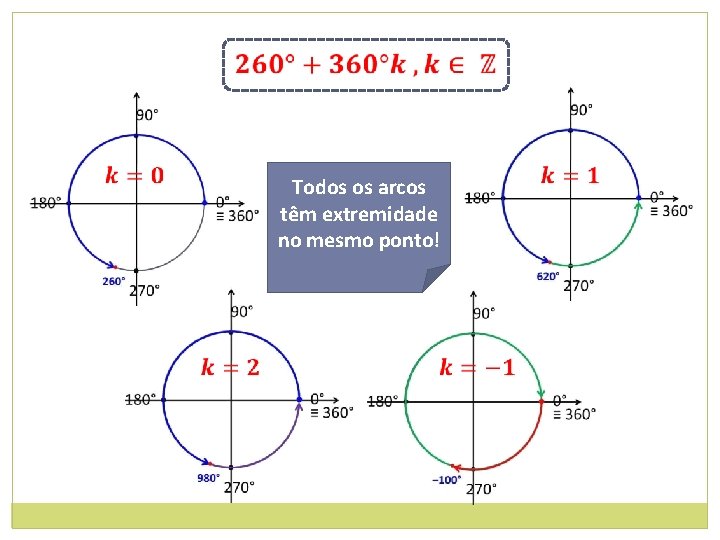
Todos os arcos têm extremidade no mesmo ponto!

b) ⇒ 1ª determinação positiva de – 700° = 360° – 340° = 20° Logo a expressão geral é c) Logo a expressão geral é

d) Logo a expressão geral é e) – 2 voltas significa duas voltas no sentido horário (negativo) A 1ª determinação positiva será Logo a expressão geral é

11. Assinale com “X” os pares que representam arcos côngruos. Solução: ( ) 740° e 1460° Para que representem arcos ( ) 400° e 940° côngruos, suas extremidades ( ) deverão ser as mesmas. Isto pode comparando ser verificado as primeiras determinações de cada par.

11. Assinale com “X” os pares que representam arcos côngruos. ( ) 740° e 1460° ⊠ ( ) 400° e 940° ( ) ⊠ ( )

12. Os arcos da forma , extremidades em que quadrantes? , k ∈ ℤ , têm Solução: Atribuindo alguns valores para “k”, observa-se a regularidade dos quadrantes: Observa-se que, para valores ÍMPARES de k, a extremidade do arco pertence ao 2º quadrante e, para valores PARES, ao 1º quadrante. Logo, a resposta é 1º e 2º quadrantes.

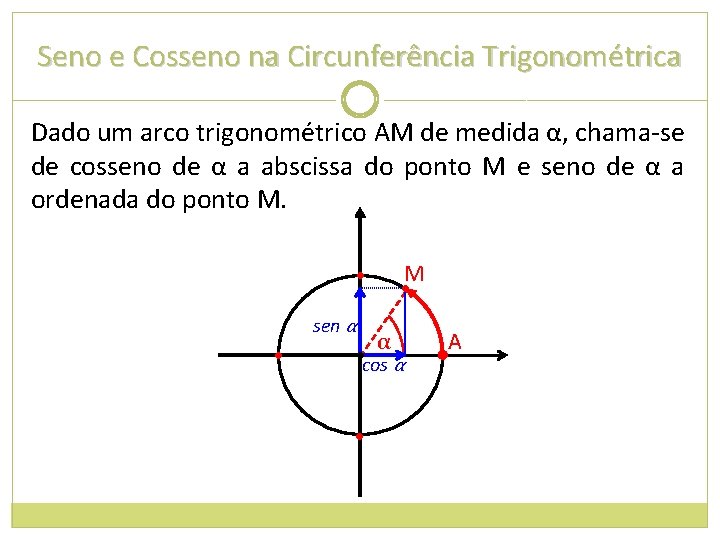
Seno e Cosseno na Circunferência Trigonométrica Dado um arco trigonométrico AM de medida α, chama-se de cosseno de α a abscissa do ponto M e seno de α a ordenada do ponto M. • sen α • M • α • cos α • A •

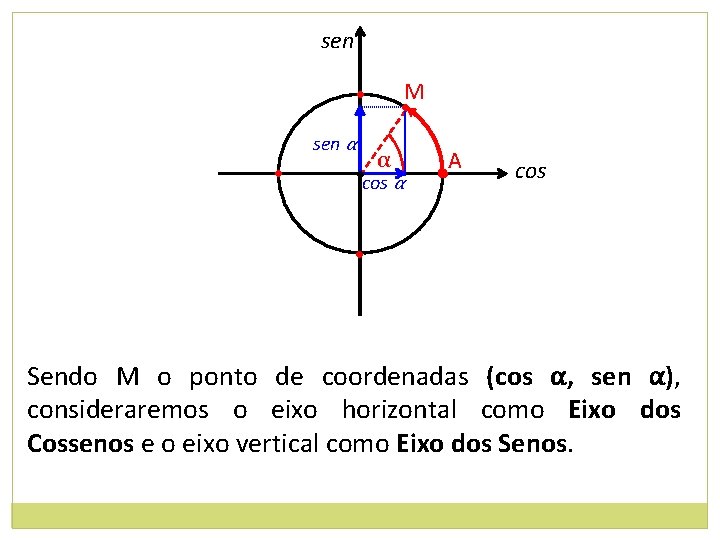
sen M • • sen α • cos α A • cos • Sendo M o ponto de coordenadas (cos α, sen α), consideraremos o eixo horizontal como Eixo dos Cossenos e o eixo vertical como Eixo dos Senos.

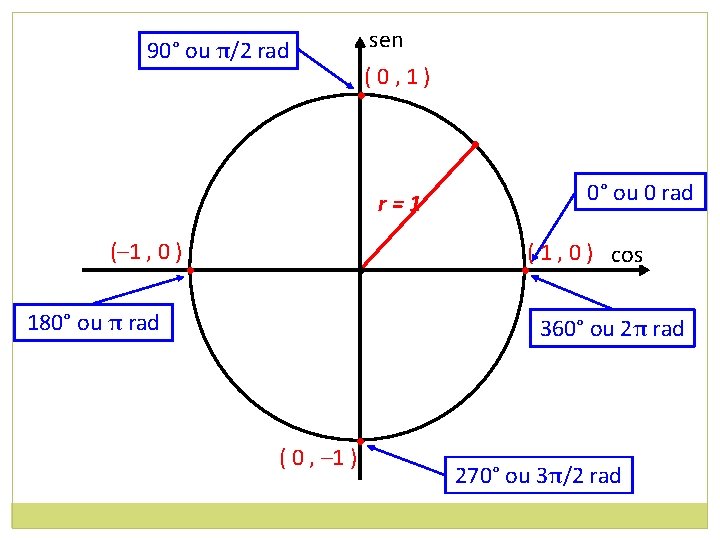
90° ou π/2 rad sen (0, 1) • • r=1 (– 1 , 0 ) • • 180° ou π rad 0° ou 0 rad ( 1 , 0 ) cos • 360° ou 2π rad • ( 0 , – 1 ) 270° ou 3π/2 rad

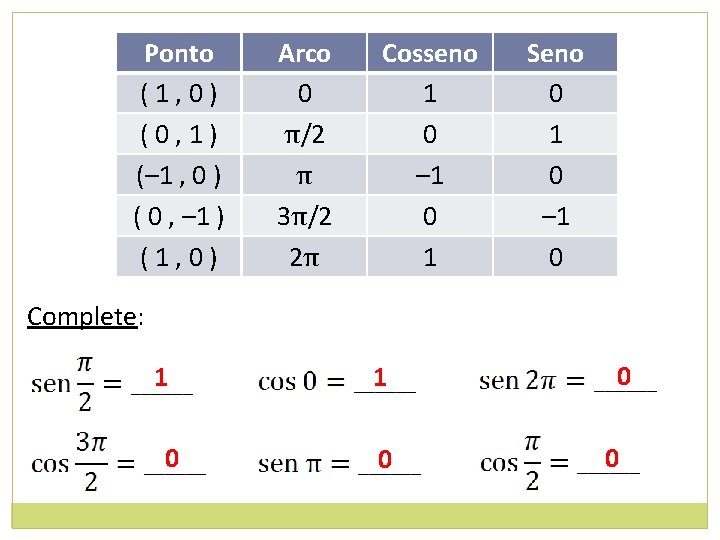
Ponto (1, 0) (0, 1) (– 1 , 0 ) ( 0 , – 1 ) (1, 0) Arco 0 π/2 π 3π/2 2π Cosseno 1 0 – 1 0 1 Seno 0 1 0 – 1 0 Complete: 1 0 0 0

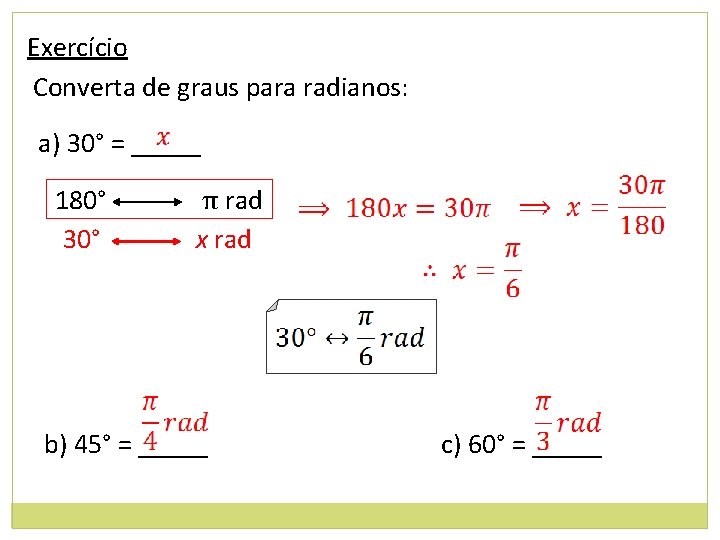
Exercício Converta de graus para radianos: a) 30° = _____ 180° 30° π rad x rad b) 45° = _____ c) 60° = _____

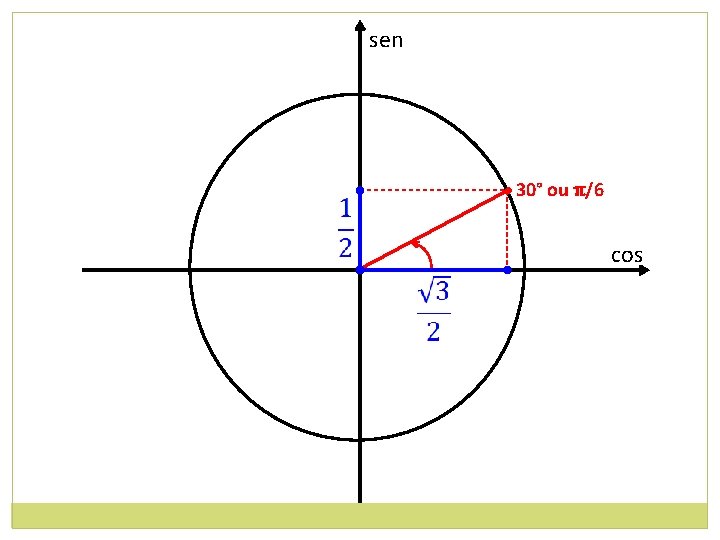
sen • 30° ou π/6 • cos

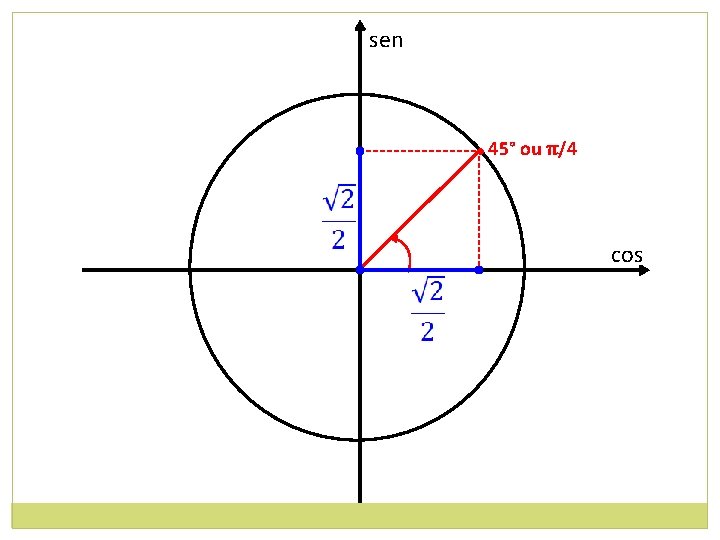
sen • 45° ou π/4 • cos

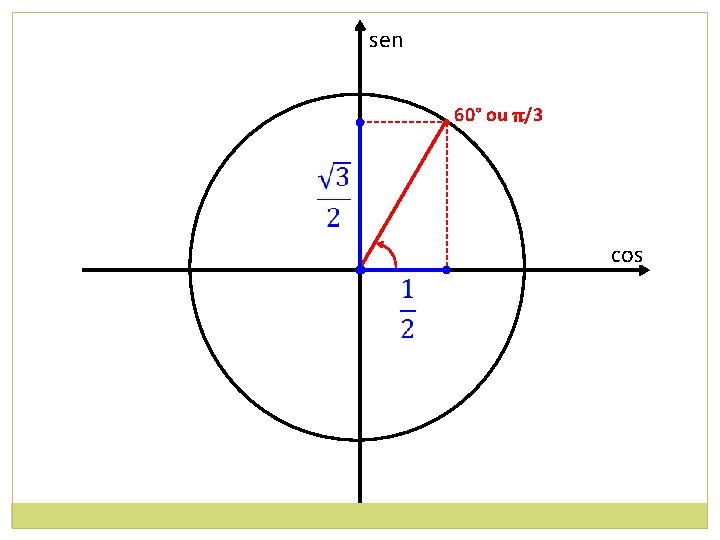
sen • 60° ou π/3 • cos

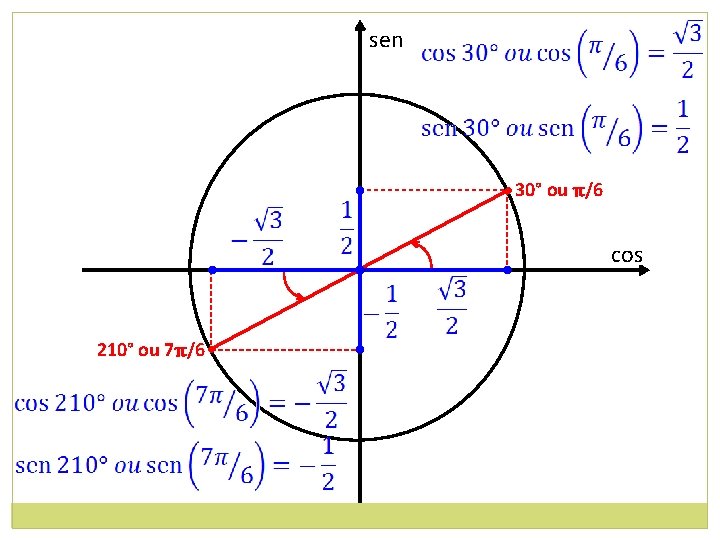
sen • 30° ou π/6 • 210° ou 7π/6 • cos

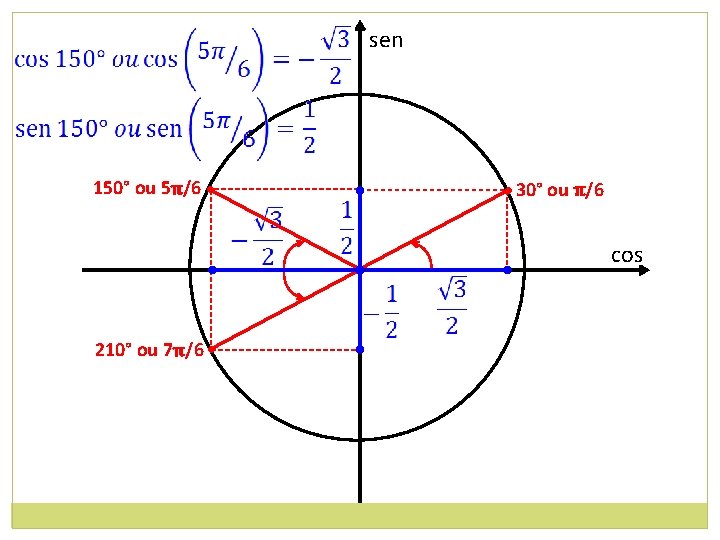
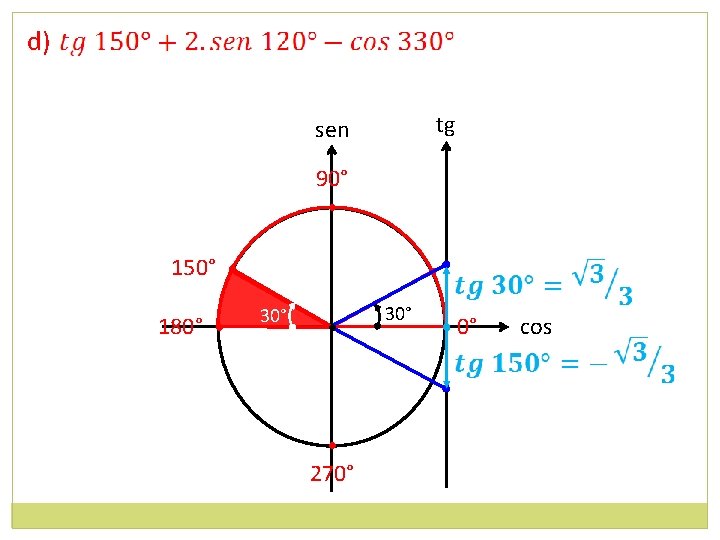
sen 150° ou 5π/6 • • 30° ou π/6 • 210° ou 7π/6 • cos

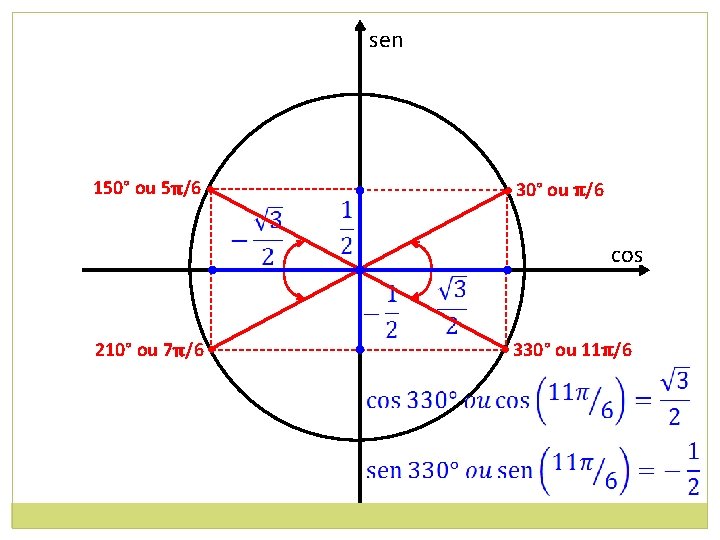
sen 150° ou 5π/6 • • 30° ou π/6 • 210° ou 7π/6 • cos • 330° ou 11π/6

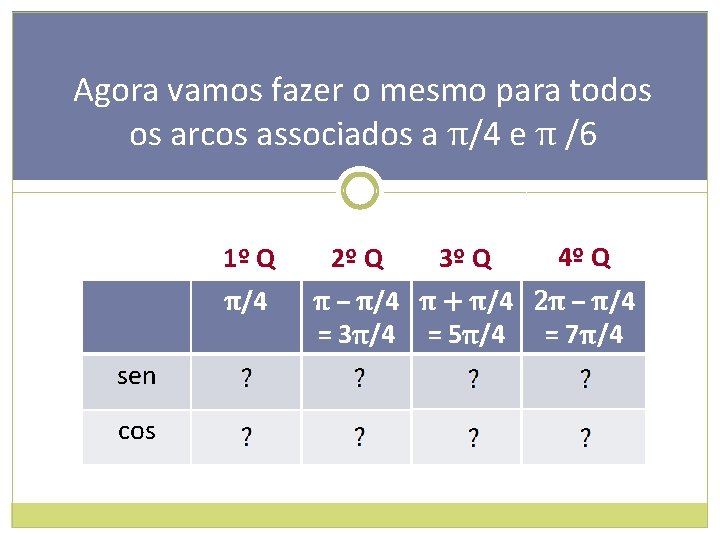
Agora vamos fazer o mesmo para todos os arcos associados a π/4 e π /6 1º Q π/4 sen cos 2º Q 3º Q 4º Q π – π/4 π + π/4 2π – π/4 = 3π/4 = 5π/4 = 7π/4

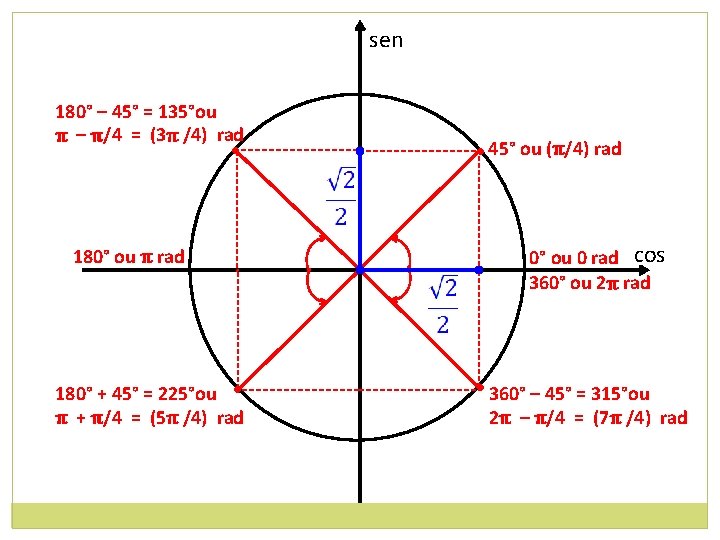
sen 180° – 45° = 135°ou π – π/4 = (3π /4) rad • 45° ou (π/4) rad • 180° ou π rad 0° ou 0 rad cos 360° ou 2π rad • • • 180° + 45° = 225°ou π + π/4 = (5π /4) rad 360° – 45° = 315°ou 2π – π/4 = (7π /4) rad

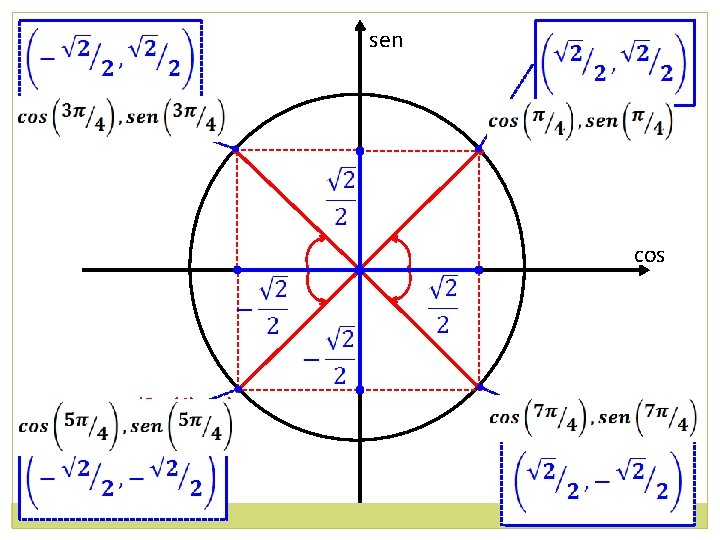
sen (3π /4) rad • • (π/4) rad cos • • • (5π /4) rad (7π /4) rad

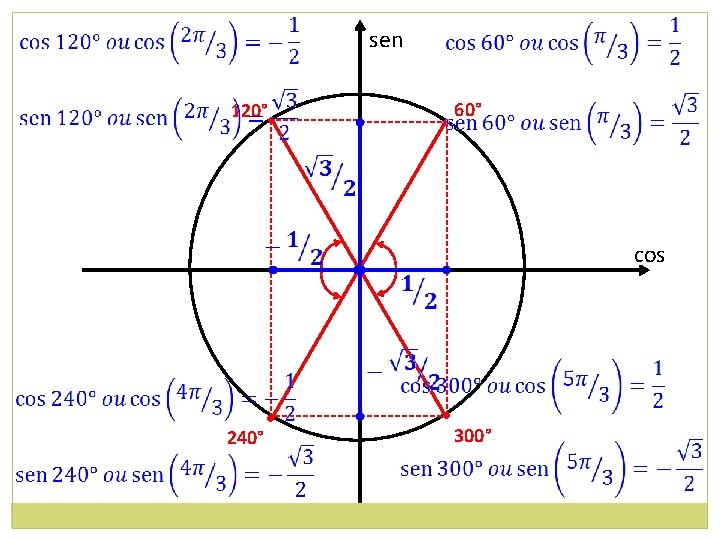
sen 180° ou π rad 0° ou 0 rad cos 360° ou 2π rad • • 180° + 60° = 240°ou π + π/3 = (4π /3) rad • 60° ou (π/3) rad • • 180° – 60° = 120°ou π – π/3 = (2π /3) rad 360° – 60° = 300°ou 2π – π/3 = (5π /3) rad

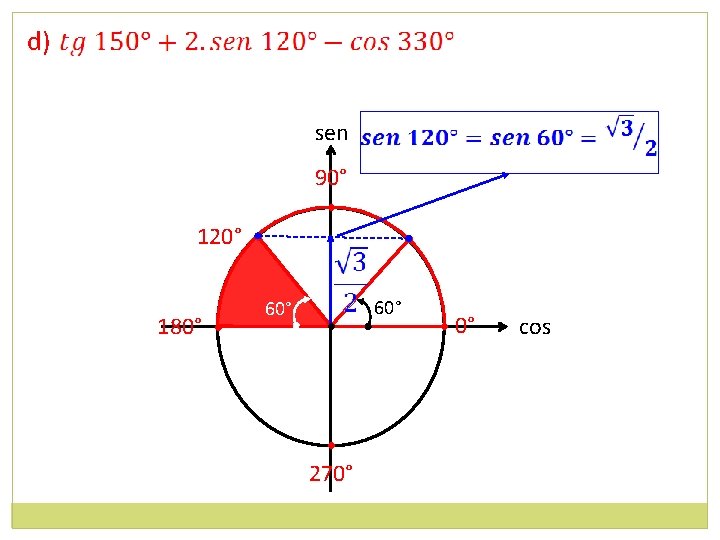
sen 120° • • 60° cos • • • 240° 300°

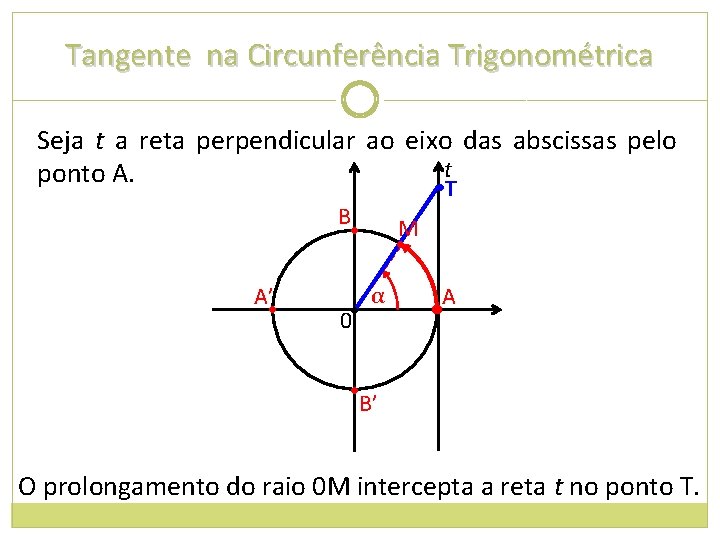
Tangente na Circunferência Trigonométrica Seja t a reta perpendicular ao eixo das abscissas pelo t ponto A. • T B • A’ • 0 • M • α A • • B’ O prolongamento do raio 0 M intercepta a reta t no ponto T.

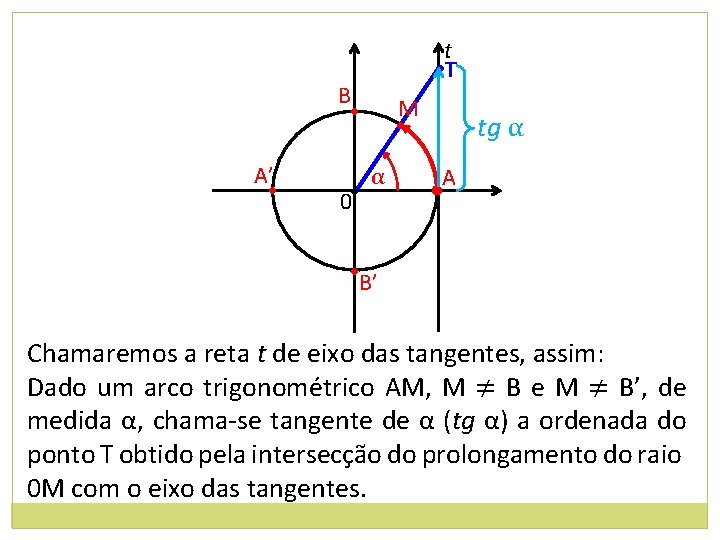
t • T B • A’ • 0 • M • α tg α A • • B’ Chamaremos a reta t de eixo das tangentes, assim: Dado um arco trigonométrico AM, M ≠ B e M ≠ B’, de medida α, chama-se tangente de α (tg α) a ordenada do ponto T obtido pela intersecção do prolongamento do raio 0 M com o eixo das tangentes.

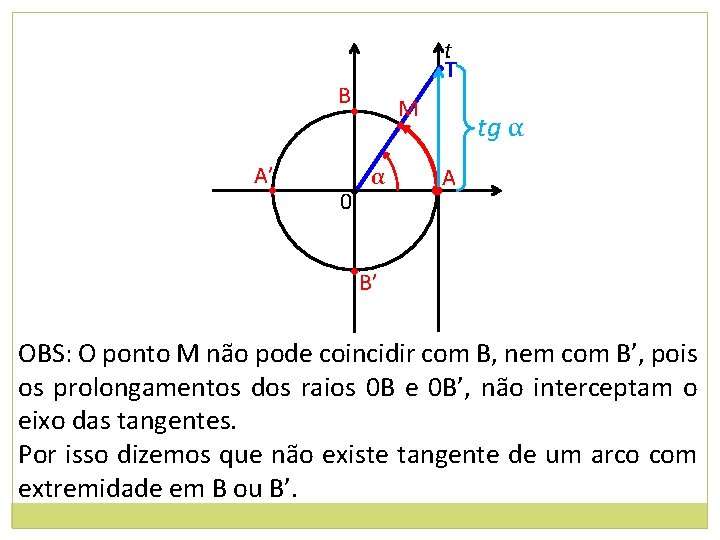
t • T B • A’ • 0 • M • α tg α A • • B’ OBS: O ponto M não pode coincidir com B, nem com B’, pois os prolongamentos dos raios 0 B e 0 B’, não interceptam o eixo das tangentes. Por isso dizemos que não existe tangente de um arco com extremidade em B ou B’.

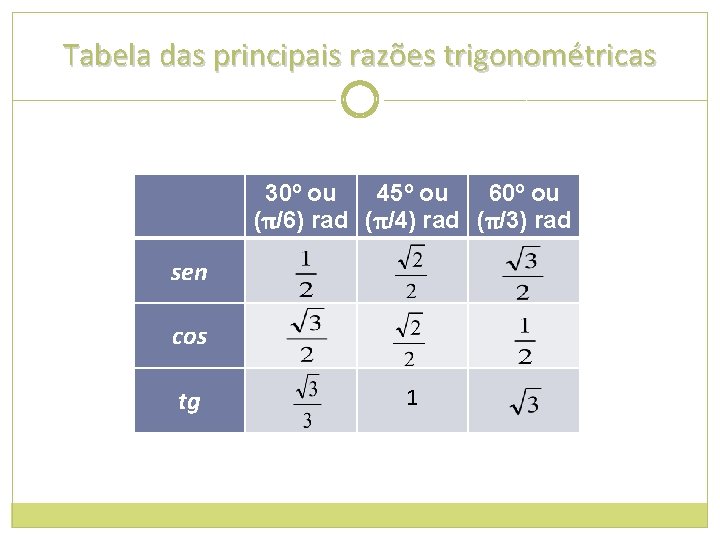
Tabela das principais razões trigonométricas 30º ou 45º ou 60º ou (π/6) rad (π/4) rad (π/3) rad sen cos tg 1

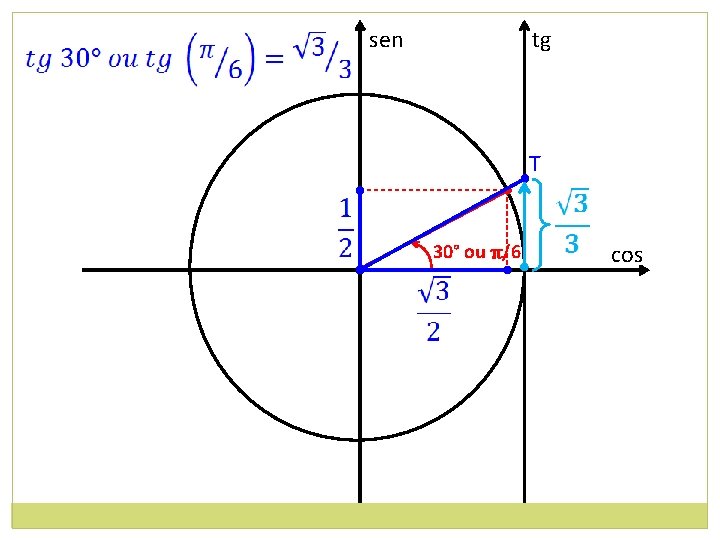
sen tg T • • 30° ou π/6 cos

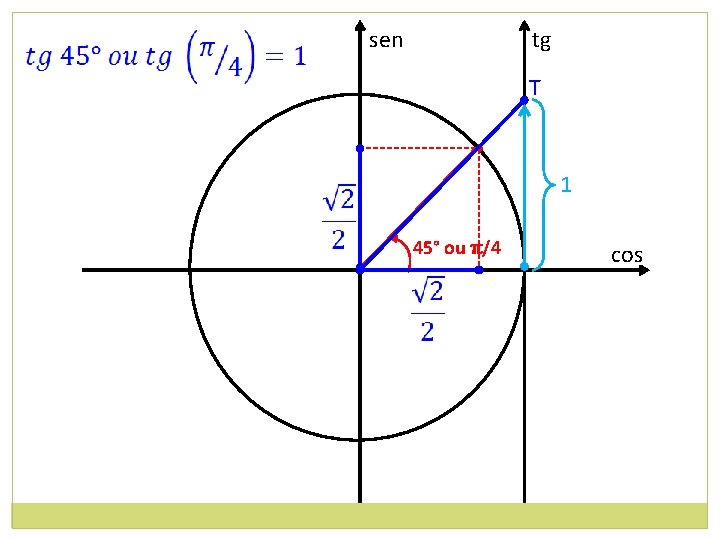
sen tg T • 1 • 45° ou π/4 cos

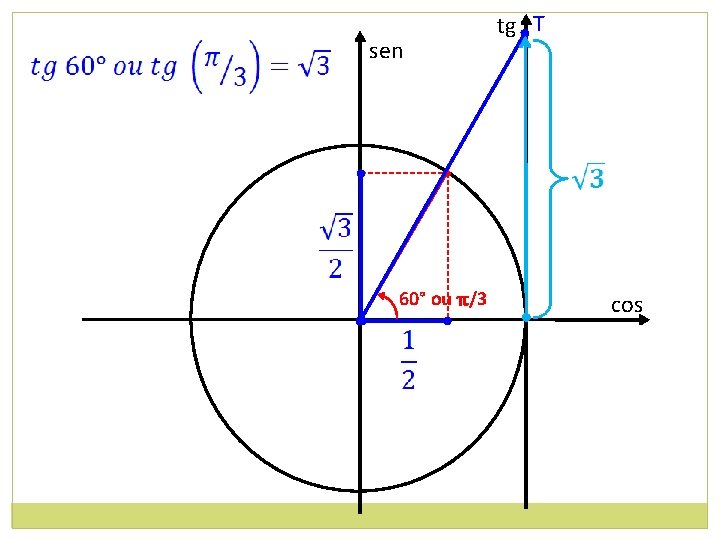
tg T sen • • 60° ou π/3 cos

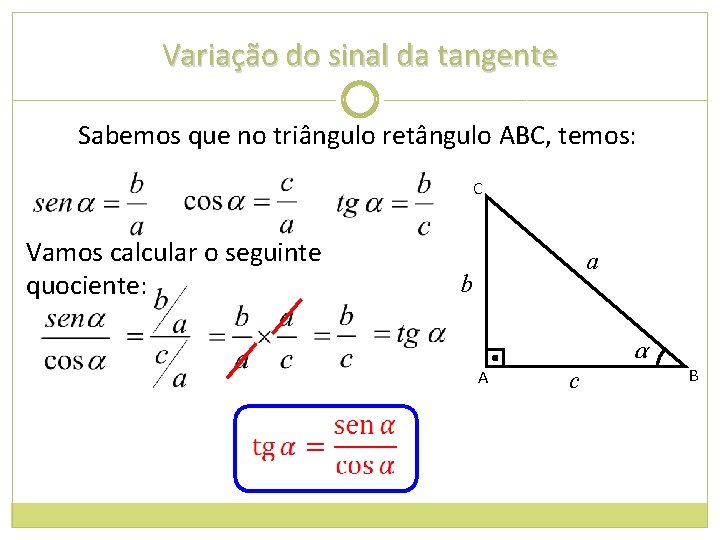
Variação do sinal da tangente Sabemos que no triângulo retângulo ABC, temos: C Vamos calcular o seguinte quociente: a b α A c B

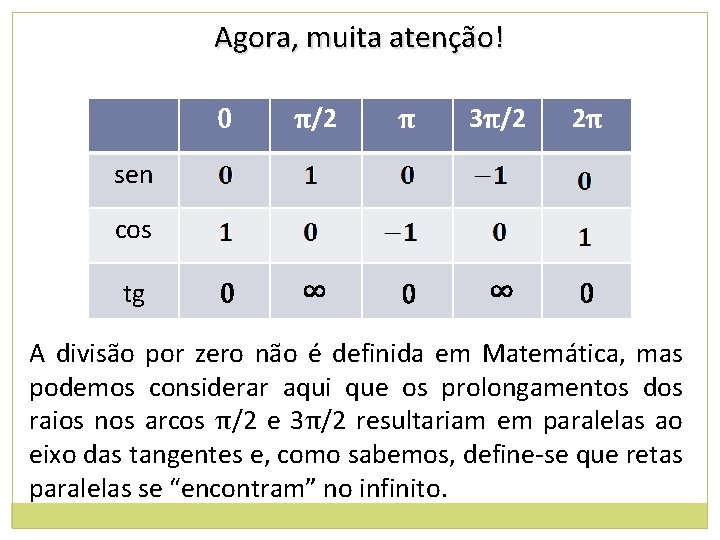
Agora, muita atenção! 0 π/2 π 3π/2 2π 0 ∞ 0 sen cos tg A divisão por zero não é definida em Matemática, mas podemos considerar aqui que os prolongamentos dos raios nos arcos π/2 e 3π/2 resultariam em paralelas ao eixo das tangentes e, como sabemos, define-se que retas paralelas se “encontram” no infinito.

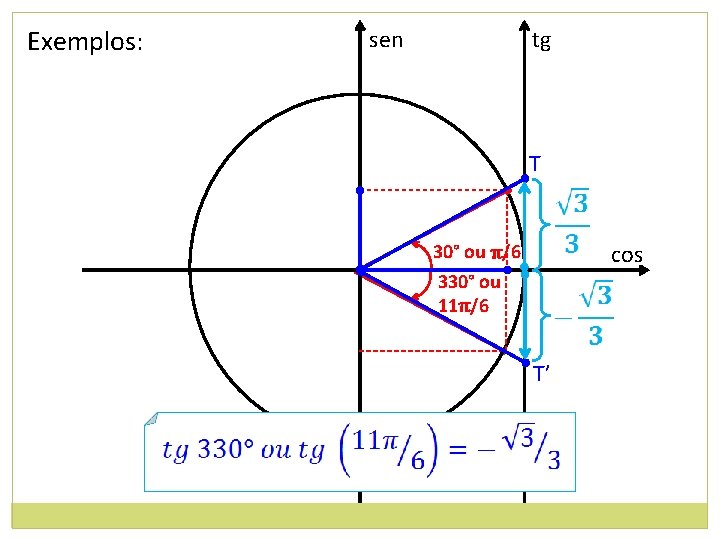
Exemplos: sen tg T • • • cos 30° ou π/6 330° ou 11π/6 T’

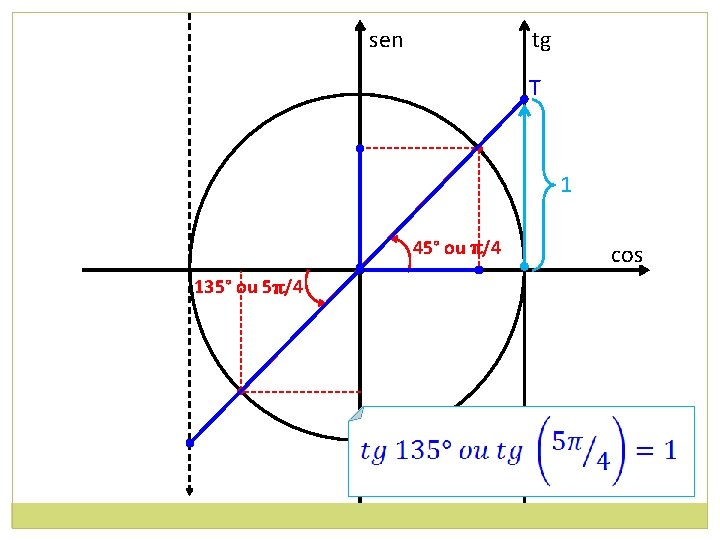
sen tg T • 1 135° ou 5π/4 • 45° ou π/4 cos •

tg T sen • • 120° ou 2π/3 • 60° ou π/3 cos

Exercícios CONTINUAÇÃO

13. Determine os valores de: a) b) Solução: Encontram-se os arcos côngruos, reduzindo ao 1° quadrante para determinações dos valores das funções e atribuindo seus respectivos sinais de acordo com os quadrantes.

a) b)

14. Determine os valores máximos e mínimos das expressões: a) b) c) Solução: As funções seno e cosseno variam no intervalo [ – 1 , 1] onde (– 1) é mínimo e (1) é máximo. No caso das funções estarem ao quadrado, o valor mínimo passa a ser (0), pois nenhum número ao quadrado pode ser negativo.

ATENÇÃO! a)

b) c)

15. Que valores de m satisfarão a ambas as condições: Solução: Aplicando a relação fundamental relacionando senos e cossenos, temos: ou

16. Sendo x um arco do 2° quadrante e , determine: a) cos x b) tg x Solução: No 2° quadrante o cosseno é negativo e a tangente também é negativa. Aplicando as relações fundamentais, temos:

a) b)

17. Relacione as colunas: Solução: Encontrando o arco côngruo correspondente, avalia-se o sinal da função.

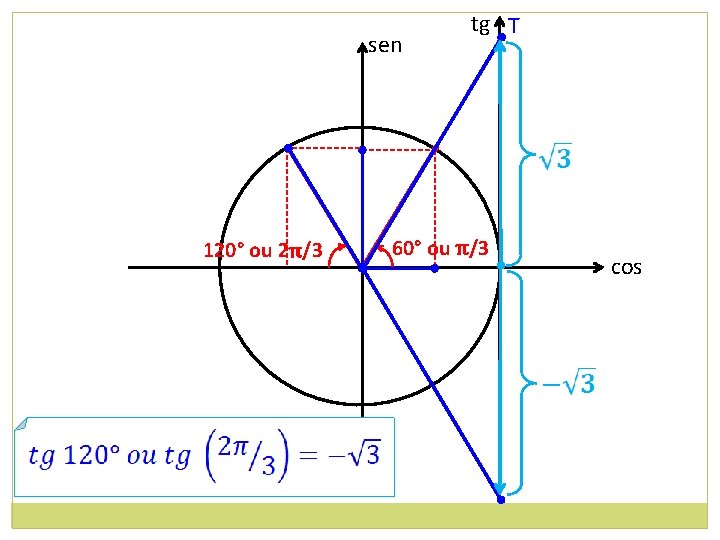
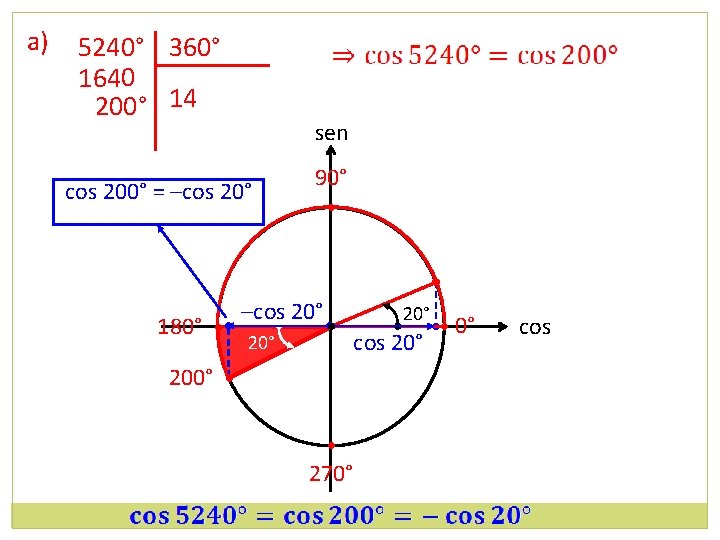
a) 5240° 360° 1640 200° 14 sen cos 200° = –cos 20° 180° • 90° • –cos 20° • 200° • • 270° 20° cos 20° • 0° cos

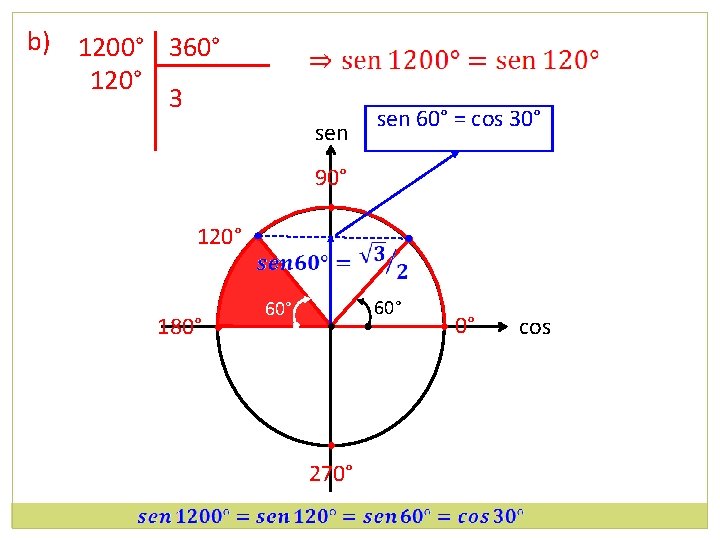
b) 1200° 360° 120° 3 sen 60° = cos 30° 90° • 120° • 180° • 60° • • 270° 60° • 0° cos

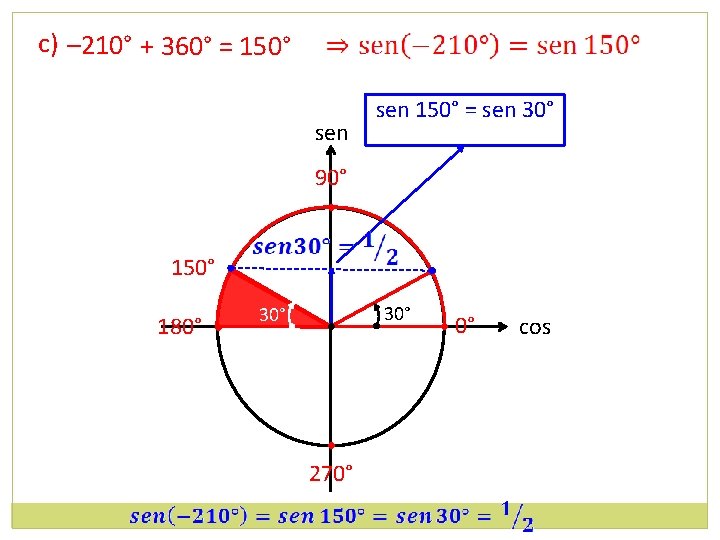
c) – 210° + 360° = 150° sen 150° = sen 30° 90° • 150° • 180° • 30° • • 270° 30° • 0° cos

d) tg sen 90° • 150° • 180° • 30° • • 270° 30° • 0° cos

d) sen 90° • 120° • 180° • 60° • • 270° 60° • 0° cos

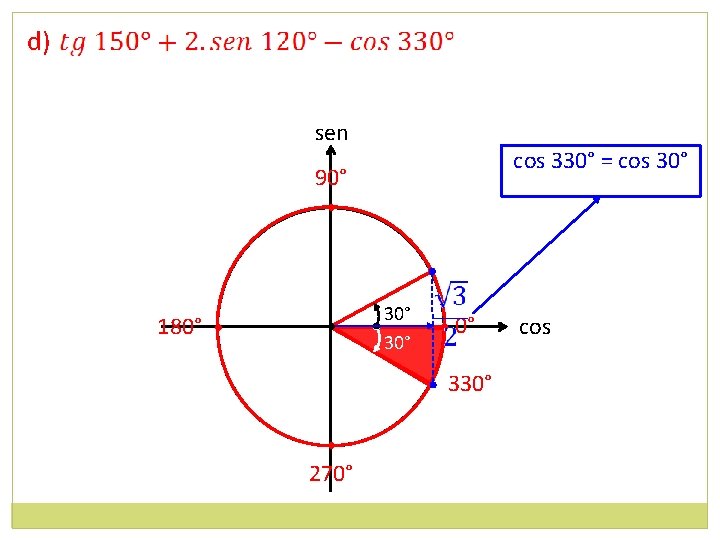
d) sen cos 330° = cos 30° 90° • 180° • • 30° • 0° • 330° • 270° cos

d)

17. Relacione as colunas:

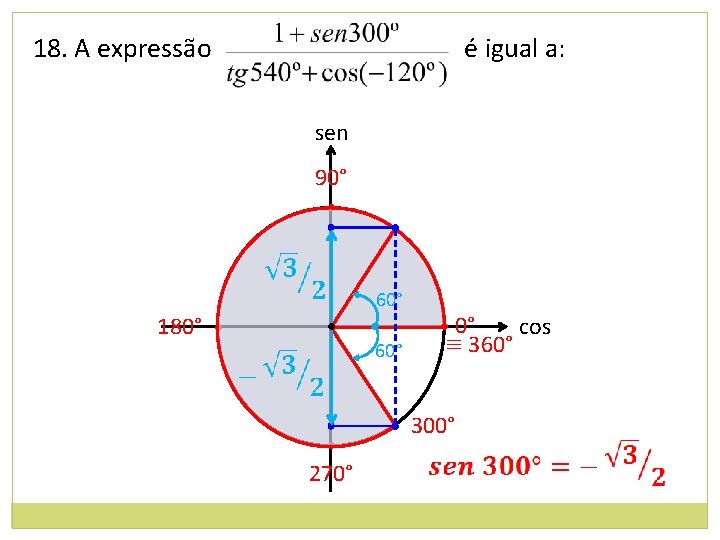
18. A expressão é igual a: sen 90° • 180° • 60° • • 270° 60° • 0° cos ≡ 360° • 300°

540° 360° 180° 1 sen tg 90° • 180° • • • 270° • 0° cos

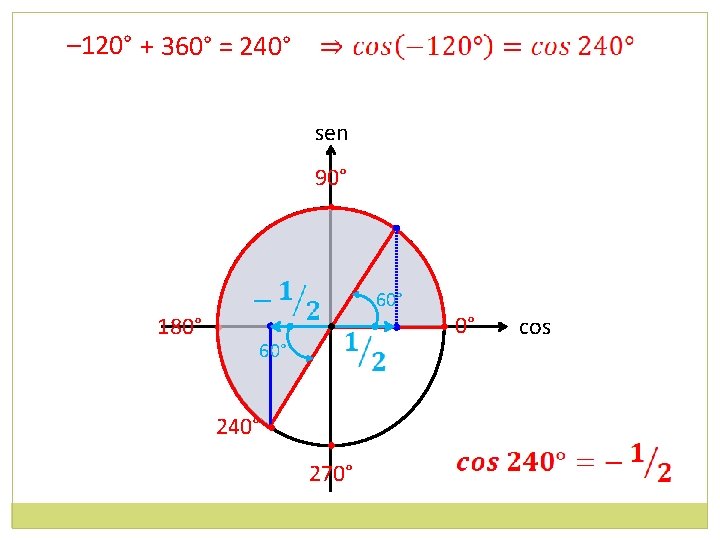
– 120° + 360° = 240° sen 90° • 180° • 60° 240° • • • 270° • 0° cos

ISERJ – 2011 Fontes: Trabalho da Professora Gertrudes, PUC-RS e http: //professorwaltertadeu. mat. br/