Chapter 2 Firstorder Differential Equations Chapter 1 Introduction































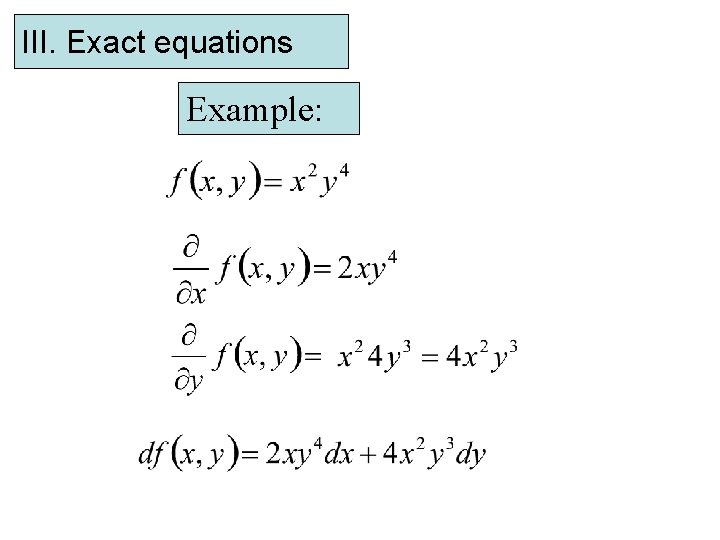













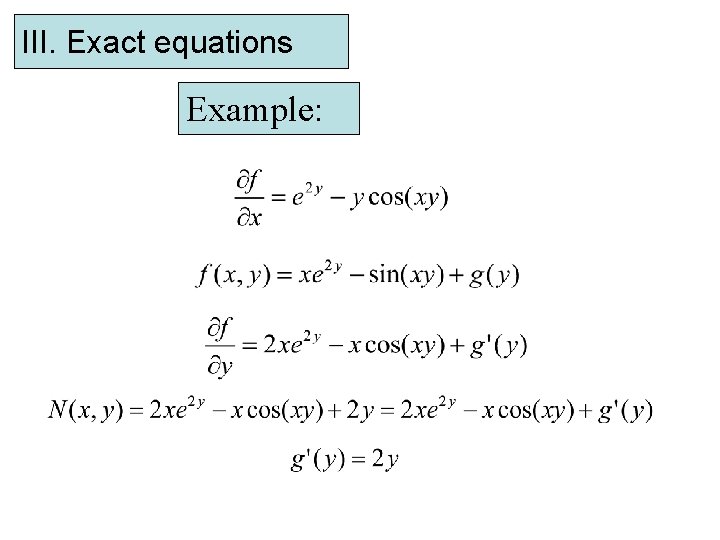


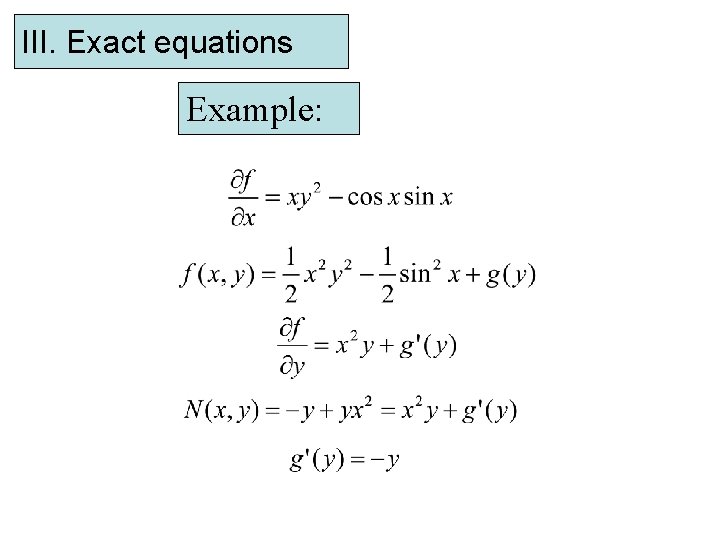
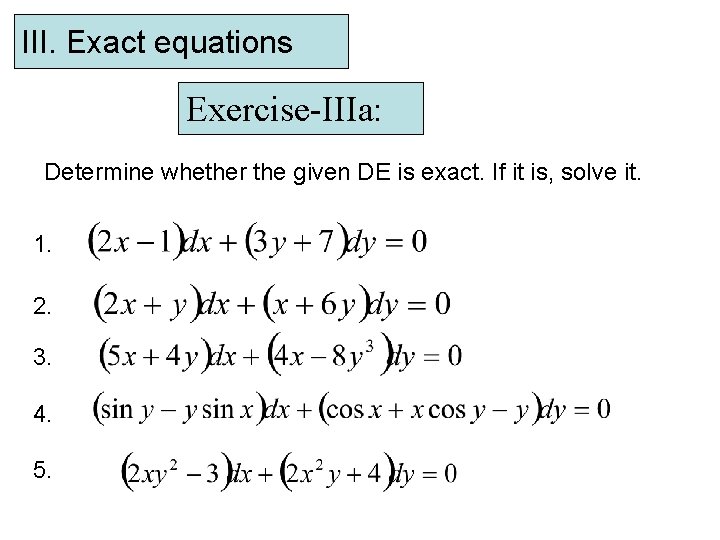

























- Slides: 84

Chapter 2 First-order Differential Equations

Chapter 1: Introduction to Differential Equations Overview I. Separable variables II. Linear equations III. Exact Equations IV. Solution by substitutions

I. Separable variables Learning Objective At the end of this section you should be able to identify and solve a separable DE.

I. Separable variables Definition A first-order DE of the form is said to be separable or to have separable variables.

I. Separable variables Examples: is separable Indeed, is not separable Indeed, it cannot be put on the product form

I. Separable variables Remark: By dividing by , the separable DE, can be written in the form: where

I. Separable variables Method of solution: From the form : we have to integrated both sides. to obtain One-parameter family of implicit or explicit solutions.

I. Separable variables Examples:

I. Separable variables Examples:

I. Separable variables Examples: . So, the solution of the IVP:

I. Separable variables Examples: .

I. Separable variables Examples: Solution of IVP: .

I. Separable variables Exercise I: Solve the following DE by separation of variables: .

II. Linear equations Learning Objective At the end of this section you should be able to identify and solve a linear DE.

II. Linear Equations Definition A first-order DE of the form is said to be linear equation in the dependent variable .

II. Linear Equations Remark By dividing both sides by written in the standard form: , a linear equation can be

II. Linear Equations Definition Values of that will make points of the equation. Example: is a singular point. , are called singular

II. Linear Equations Definition The function factor. Remark: is defined as the integrating

II. Linear Equations Examples: Find the integrating factor for : 1)

II. Linear Equations Examples: Find the integrating factor for : 2) Singular point :

II. Linear Equations Method of solution 1) Write the standard form : 2) Find the integrating factor :

II. Linear Equations Method of solution 3) Multiply the Standard form by the integrating factor : Standard form :

II. Linear Equations Method of solution 4) Integrate both sides of the last equation :

II. Linear Equations Examples: Solve the following linear DE : 1)

II. Linear Equations Examples: 1)

II. Linear Equations Examples: 2)

II. Linear Equations Examples: 2) Valid on

II. Linear Equations Exercise-II: Solve the following linear DE :

III. Exact equations Learning Objective At the end of this section you should be able to identify and solve an exact ODE.

III. Exact equations Definition Consider a function of two variables: is the partial derivative of regarding ( is considered as a constant).

III. Exact equations Definition Consider a function of two variables: its differential is :
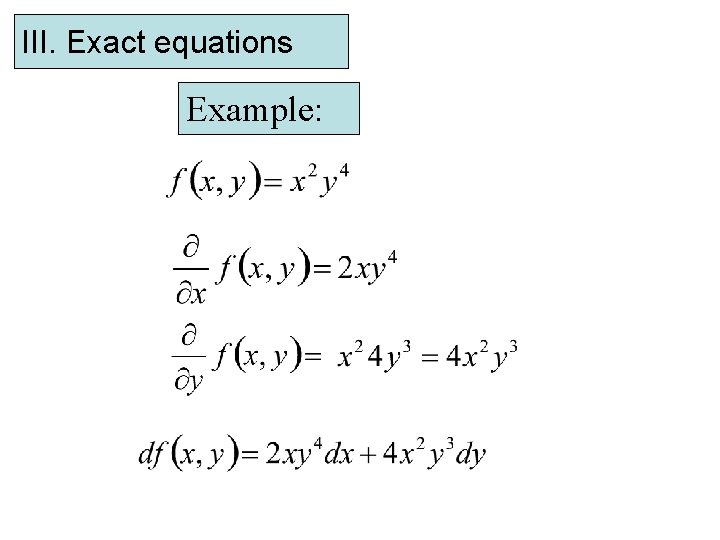
III. Exact equations Example:

III. Exact equations Examples:

III. Exact equations Definition A differential expression : is an exact differential if it corresponds to the differential of some function that means

III. Exact equations Example is an exact differential Indeed

III. Exact equations Definition A DE of the form: is an exact equation if the left side is an exact differential. In that case, the DE is equivalent to An implicit solution will be

III. Exact equations Example is an exact equation Indeed

III. Exact equations Theorem A necessary and sufficient condition that be an exact differential is .

III. Exact equations Example Indeed exact equation

III. Exact equations Method of solution Example: Step 1: Check exactitude ? . Exact DE there exists such that

III. Exact equations Method of solution Step 2: integrate regarding . constant for but not for

III. Exact equations Method of solution Step 3: Differentiate regarding .

III. Exact equations Method of solution Step 4: Integrate regarding .

III. Exact equations Method of solution Step 5: Solution An implicit solution is . An explicit solution is defined when

III. Exact equations Example: Solve the following ODEs: exact equation
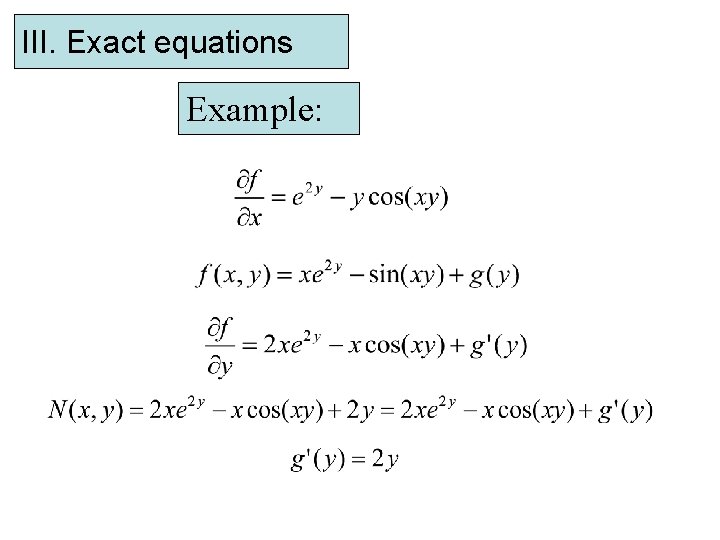
III. Exact equations Example:

III. Exact equations Example: Implicit solution

III. Exact equations Example: exact equation
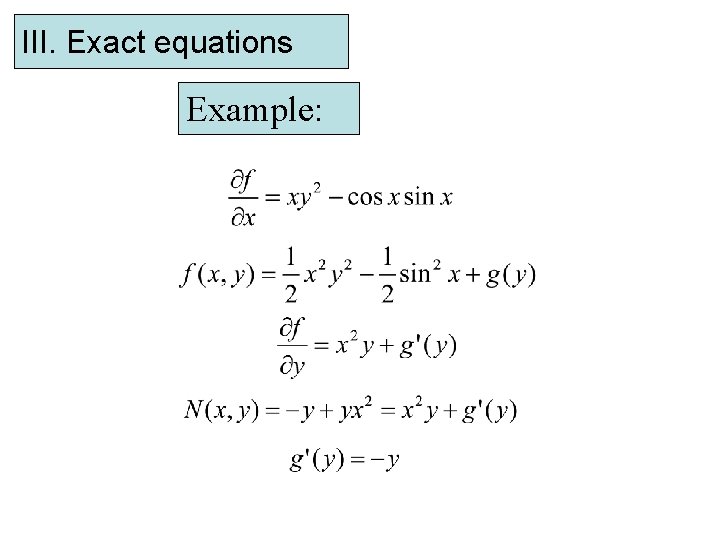
III. Exact equations Example:

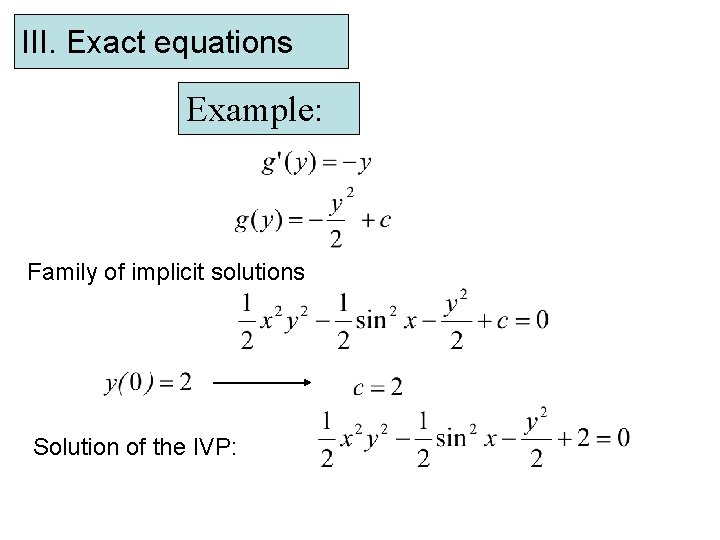
III. Exact equations Example: Family of implicit solutions Solution of the IVP:
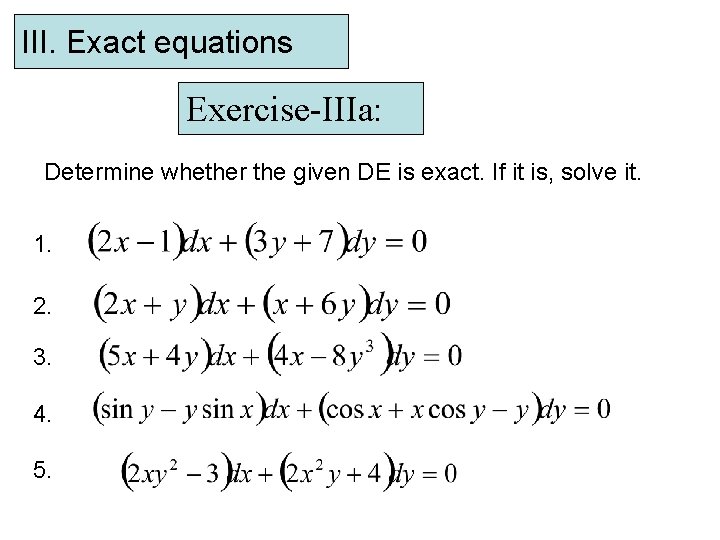
III. Exact equations Exercise-IIIa: Determine whether the given DE is exact. If it is, solve it. 1. 2. 3. 4. 5.

III. Exact equations Remark: make exact some non-exact DEs is non exact if where There are cases where the equation can be made exact. How?

III. Exact equations Remark: make exact some non-exact DE compute If the result is a function of the sole variable then find the integrating factor : :

III. Exact equations Remark: make exact some non-exact DE Multiply the DE by the integrating factor : Now Exact!

III. Exact equations Remark: make exact some non-exact DE Example

III. Exact equations Remark: make exact some non-exact DE Example Exact!

III. Exact equations Remark: make exact some non-exact DE If is NOT a function of the unique variable compute If the result is a function of the sole variable then find the integrating factor : :

III. Exact equations Remark: make exact some non-exact DE Example

III. Exact equations Remark: make exact some non-exact DE Example Exact!

III. Exact equations Exercise-IIIb: Solve the given D. E by finding an appropriate integrating factor. 1. 2. 3. 4.

IV. Solution by substitutions Learning Objective At the end of this section you should be able to solve Homogeneous and Bernoulli’s DEs.

IV. Solution by substitutions Bernoulli Equation Definition : A DE in the form real number is said a Bernoulli equation. where is a

IV. Solution by substitutions Bernoulli Equation Example :

IV. Solution by substitutions Bernoulli Equation Substitution:

IV. Solution by substitutions Bernoulli Equation

IV. Solution by substitutions Bernoulli Equation Example :

IV. Solution by substitutions Bernoulli Equation Example :

IV. Solution by substitutions Bernoulli Equation Example :

IV. Solution by substitutions Bernoulli Exercise IVb : Solve the given Bernoulli equation by using an appropriate substitution.

IV. Solution by substitutions Homogeneous DE Definition : If a function has the property that for some real number , then homogeneous function of degree. , is said to be a

IV. Solution by substitutions Homogeneous DE Example 1 : is a homogeneous function of degree 2.

IV. Solution by substitutions Homogeneous DE Example 2 : is a homogeneous function of degree 2/3.

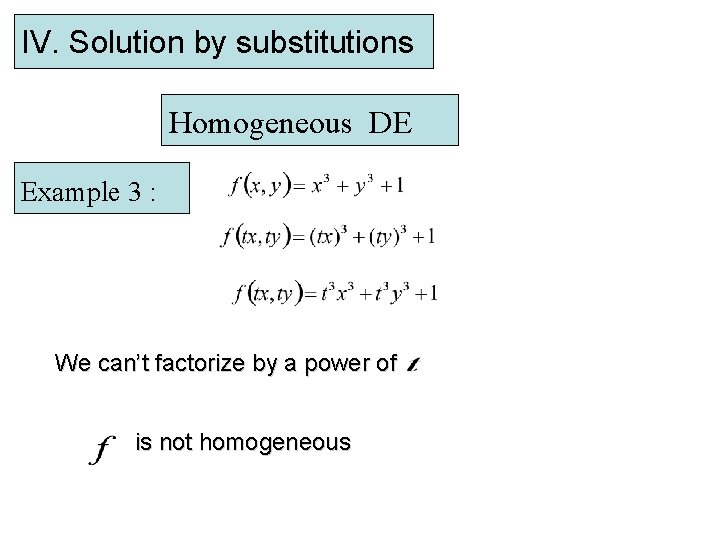
IV. Solution by substitutions Homogeneous DE Example 3 : We can’t factorize by a power of is not homogeneous

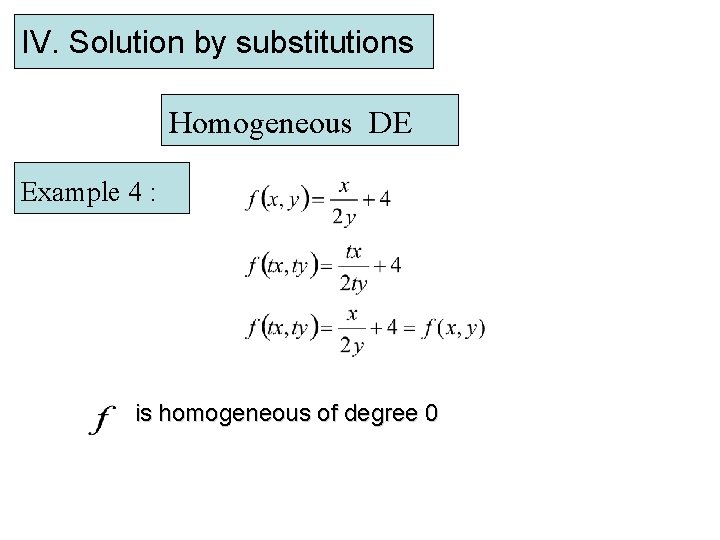
IV. Solution by substitutions Homogeneous DE Example 4 : is homogeneous of degree 0

IV. Solution by substitutions Homogeneous DE Definition : A DE of the form homogeneous if both and functions of the same degree. is said to be are homogeneous

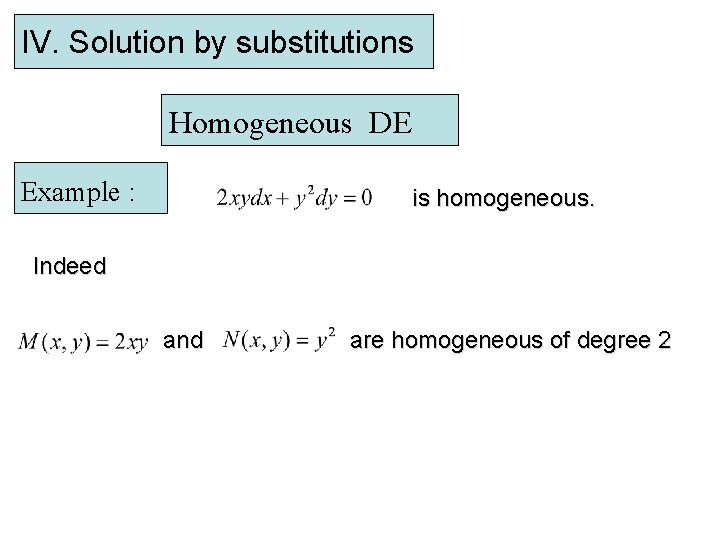
IV. Solution by substitutions Homogeneous DE Example : is homogeneous. Indeed and are homogeneous of degree 2

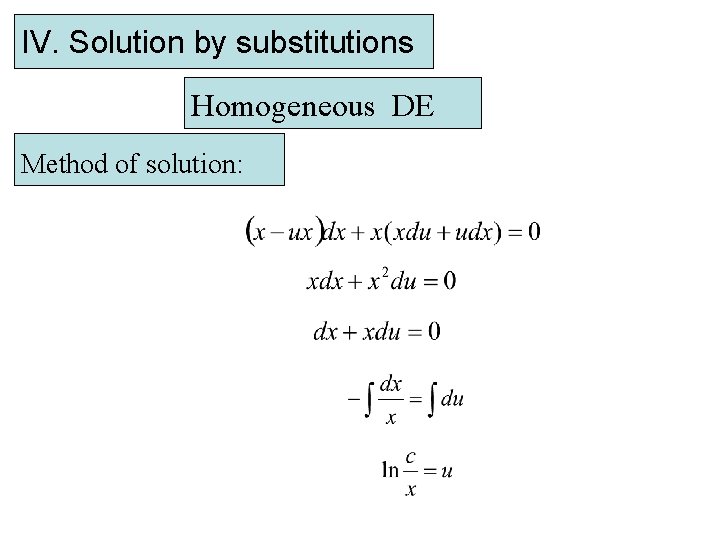
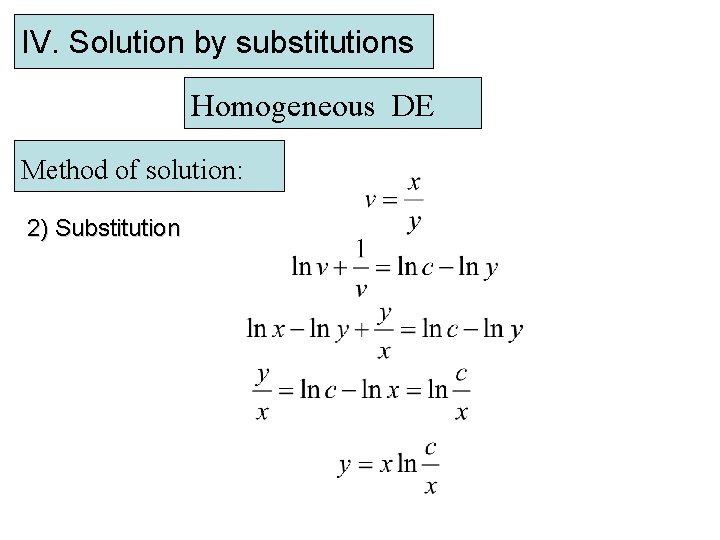
IV. Solution by substitutions Homogeneous DE Method of solution: 1) Homogeneity : and are homogeneous of degree 1 2) Substitution

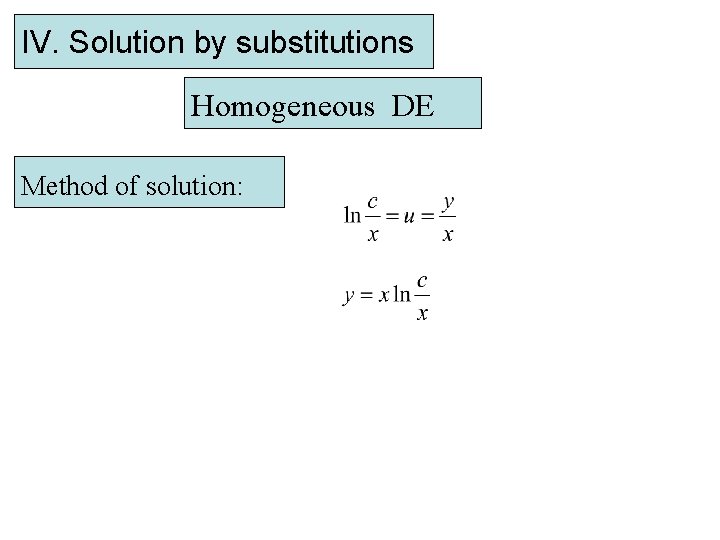
IV. Solution by substitutions Homogeneous DE Method of solution:

IV. Solution by substitutions Homogeneous DE Method of solution:

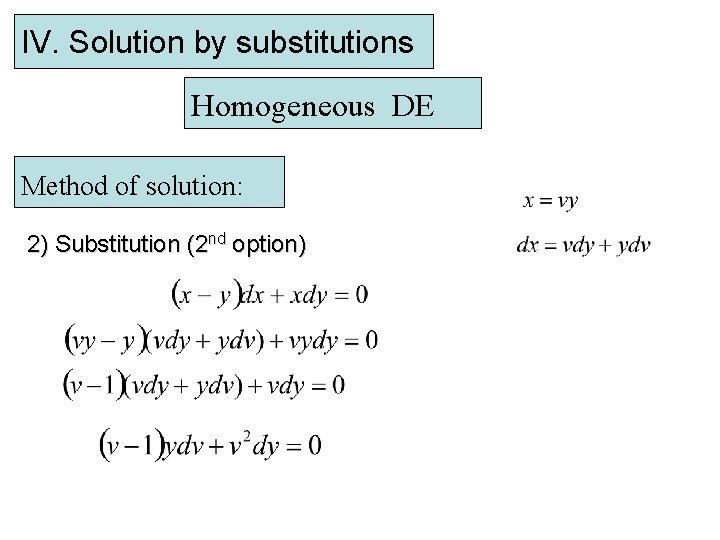
IV. Solution by substitutions Homogeneous DE Method of solution: 2) Substitution (2 nd option)

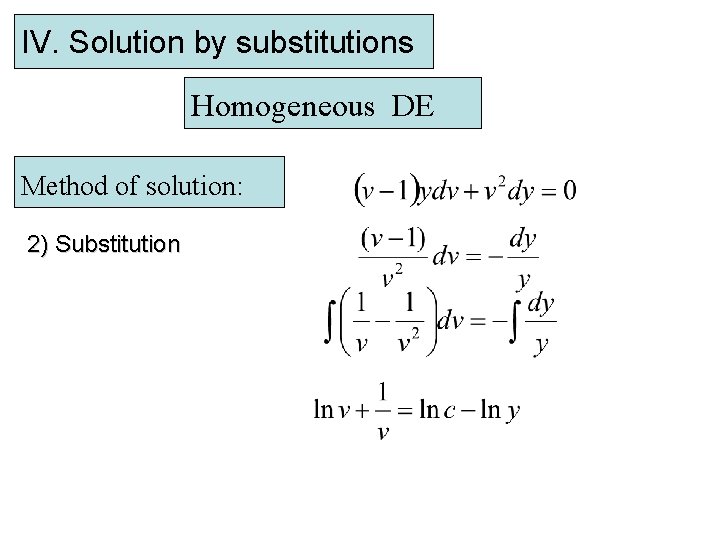
IV. Solution by substitutions Homogeneous DE Method of solution: 2) Substitution

IV. Solution by substitutions Homogeneous DE Method of solution: 2) Substitution

IV. Solution by substitutions Homogeneous DE Exercise IVa : Solve the given homogeneous equation by using an appropriate substitution.

End Chapter 2
 Differential equations chapter 1
Differential equations chapter 1 Differential equations projects
Differential equations projects Ordinary differential equations ppt
Ordinary differential equations ppt Classification of pde
Classification of pde Cengage differential equations
Cengage differential equations Nonlinear equations
Nonlinear equations Transient solution differential equations
Transient solution differential equations Carrying capacity equation calculus
Carrying capacity equation calculus Solution of partial differential equation
Solution of partial differential equation Separation of variables differential equations
Separation of variables differential equations Partial differential equations examples
Partial differential equations examples Solving 1st order differential equations
Solving 1st order differential equations Solving 1st order differential equations
Solving 1st order differential equations Differential equations general solution
Differential equations general solution Cengage differential equations
Cengage differential equations Natural solution
Natural solution Runge kutta second order formula
Runge kutta second order formula What is a first order equation
What is a first order equation Classification of differential equations
Classification of differential equations Traffic flow differential equations
Traffic flow differential equations First order ordinary differential equations
First order ordinary differential equations Backward euler scheme
Backward euler scheme First order linear differential equation
First order linear differential equation Variable separable
Variable separable Slidetodoc
Slidetodoc Differential equations
Differential equations Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Bernoulli's equation differential equations
Bernoulli's equation differential equations Parachute problem differential equations
Parachute problem differential equations Non homogeneous differential equation definition
Non homogeneous differential equation definition Symplectic
Symplectic Growth and decay differential equations
Growth and decay differential equations Differential equations zill solutions
Differential equations zill solutions Stewart differential equations
Stewart differential equations Hertz
Hertz Mechanical and electrical vibrations
Mechanical and electrical vibrations Cauchy euler equation
Cauchy euler equation Ordinary differential equations example
Ordinary differential equations example Ordinary differential equations examples
Ordinary differential equations examples Separation of variables
Separation of variables Higher order linear differential equations
Higher order linear differential equations Differential equations definition
Differential equations definition Mixing problems differential equations
Mixing problems differential equations Derivation of maxwell's equations in differential form
Derivation of maxwell's equations in differential form Differential equations with discontinuous forcing functions
Differential equations with discontinuous forcing functions Derivation of maxwell's equations in differential form
Derivation of maxwell's equations in differential form Hyperbolic partial differential equation
Hyperbolic partial differential equation Differential equations summary
Differential equations summary Ordinary differential equation
Ordinary differential equation Logistic differential equation
Logistic differential equation Solve the differential equation
Solve the differential equation Hcc differential equations
Hcc differential equations Numerical methods for partial differential equations eth
Numerical methods for partial differential equations eth Differential leveling example
Differential leveling example 9-3 polar and rectangular forms of equations
9-3 polar and rectangular forms of equations Translating chemical equations
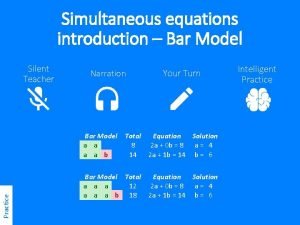
Translating chemical equations Simultaneous equations introduction
Simultaneous equations introduction First order differential equation chapter 9
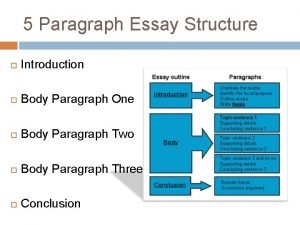
First order differential equation chapter 9 Introduction paragraph format
Introduction paragraph format Wbc
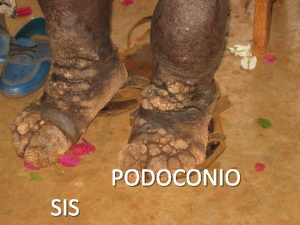
Wbc What is podoconiosis
What is podoconiosis Differential weathering examples
Differential weathering examples Circuit solution
Circuit solution Black tarry stool images
Black tarry stool images Differential form of gauss law
Differential form of gauss law Non exact differential equation
Non exact differential equation What does a human embryo look like
What does a human embryo look like Dyslexia differential diagnosis
Dyslexia differential diagnosis Partial differential protection
Partial differential protection Principle of thermogravimetric analysis
Principle of thermogravimetric analysis Differential thermal analysis
Differential thermal analysis Differential loss to follow-up
Differential loss to follow-up Cynthia dwork differential privacy
Cynthia dwork differential privacy Complexity of differential privacy
Complexity of differential privacy Differential diagnosis of jaundice in pediatrics
Differential diagnosis of jaundice in pediatrics Bowstring sign
Bowstring sign Solo hermelin
Solo hermelin General solution of partial differential equation
General solution of partial differential equation Differential association example
Differential association example Describe
Describe Differential settling method
Differential settling method Msa agar selective or differential
Msa agar selective or differential 2nd order homogeneous differential equation
2nd order homogeneous differential equation Types of differential stress
Types of differential stress Semantic differential scale
Semantic differential scale