SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS Example Write the


![SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS clc; clear; syms s; A=[0 1; -250 -2]; i SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS clc; clear; syms s; A=[0 1; -250 -2]; i](https://slidetodoc.com/presentation_image_h/27e49dfe2925cd5ec77d143910e76da5/image-3.jpg)
![SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS For v(t) clc; clear; num=[-7. 5]; den=[1 2 250]; SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS For v(t) clc; clear; num=[-7. 5]; den=[1 2 250];](https://slidetodoc.com/presentation_image_h/27e49dfe2925cd5ec77d143910e76da5/image-5.jpg)









- Slides: 16

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS Example: Write the equation of motion of the mechanical system given below in the State Variables Form. Force applied on the system is F(t)=100 u(t) (a step input having magnitude 100 Newtons) and at t=0 x 0=0. 05 m and dx/dt=0. Find x(t) and v(t). State variables are x and v=dx/dt. m=20 kg c=40 Ns/m k=5000 N/m Matlab program to obtain eigenvalues: >>a=[0 1; -250 -2]; eig(a)

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS Applying Laplace transform and arranging, Solution due to the initial conditions Solution due to the input
![SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS clc clear syms s A0 1 250 2 i SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS clc; clear; syms s; A=[0 1; -250 -2]; i](https://slidetodoc.com/presentation_image_h/27e49dfe2925cd5ec77d143910e76da5/image-3.jpg)
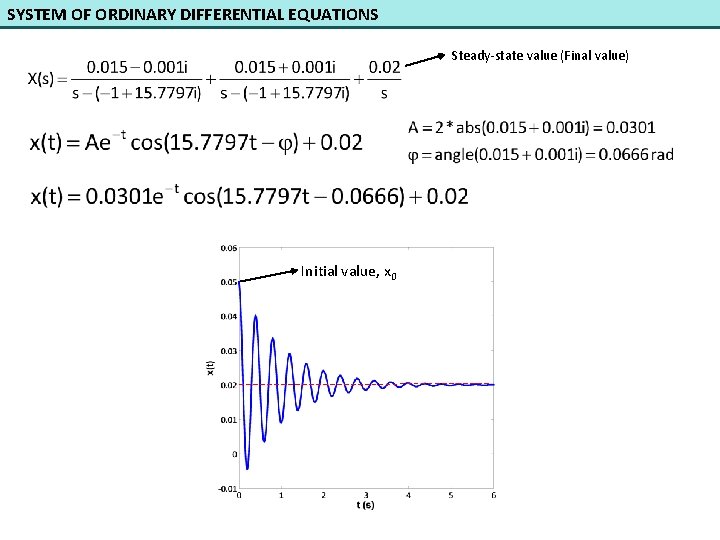
SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS clc; clear; syms s; A=[0 1; -250 -2]; i 1=eye(2); %identity matrix with dimension 2 x 2 si. A=s*i 1 -A; x 0=[0. 05; 0]; %Initial conditions B=[0; 0. 05]; Fs=100/s; X=inv(si. A)*x 0+inv(si. A)*B*Fs; pretty(X) For x(t) ; clc; clear; num=[0. 05 0. 1 5]; den=[1 2 250 0]; [r, p, k]=residue(num, den)

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS Steady-state value (Final value) Initial value, x 0
![SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS For vt clc clear num7 5 den1 2 250 SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS For v(t) clc; clear; num=[-7. 5]; den=[1 2 250];](https://slidetodoc.com/presentation_image_h/27e49dfe2925cd5ec77d143910e76da5/image-5.jpg)
SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS For v(t) clc; clear; num=[-7. 5]; den=[1 2 250]; [r, p, k]=residue(num, den)

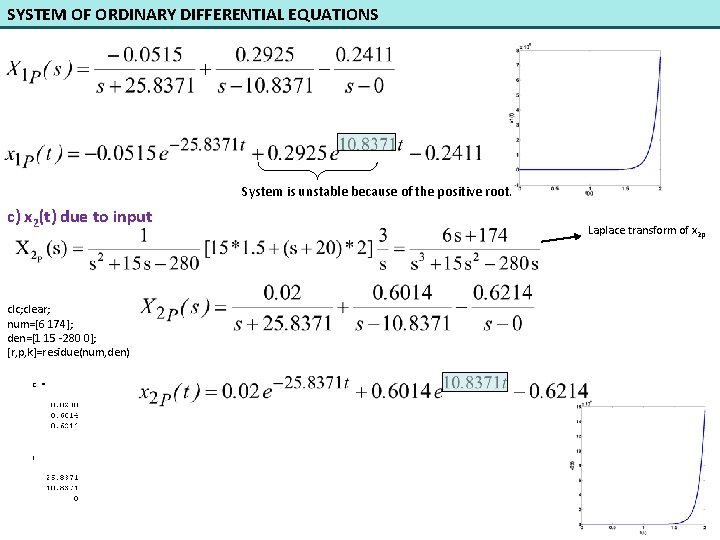
SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS Example: Mathematical model of a mechanical system is defined as a system of differential equations as follows: where f is input, x 1 are x 2 outputs. At t=0 x 1=2 and x 2=-1. a) Find the eigenvalues of the system. b) If f is a step input having magnitude of 3, find x 1(t). c) If f is a step input having magnitude of 3, find x 2(t). d) Find the response of x 1 due to the initial conditions. e) Find the response of x 2 due to the initial conditions. f) How do you obtain [s. I-A]-1 with MATLAB?

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS Let us obtain the State Variables Form so as to 1 st order derivative terms are left-hand side and non-derivative terms are on the right-hand side. State Variables Form A B D(s)

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS a) Eigenvalues are roots of the polynomial D(s) or eigenvalues of the matrix A. or b) x 1(t) due to the forcing General Solution Initial Conditions Solution due to the initial conditions Solution due to the input Particular Solution Homogeneous Solution clc; clear; num=[4. 5 67. 5]; den=[1 15 -280 0]; [r, p, k]=residue(num, den)

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS System is unstable because of the positive root. c) x 2(t) due to input clc; clear; num=[6 174]; den=[1 15 -280 0]; [r, p, k]=residue(num, den) Laplace transform of x 2 p

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS d) x 1 due to the initial conditions. clc; clear; num=[2 -25]; den=[1 15 -280]; [r, p, k]=residue(num, den) e) x 2 due to the initial conditions clc; clear; num=[-1 4]; den=[1 15 -280]; [r, p, k]= residue(num, den) f) [s. I-A]-1 with Matlab. clc; clear; syms s; i 1=eye(2) A=[-20 15; 12 5]; a 1=inv(s*i 1 -A) pretty(a 1)

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS Example: Mathematical model of a system is given below. Where V(t) is input, q 1(t) and q 2(t) are outputs. a) Write the equations in the form of state variables. b) Write Matlab code to obtain eigenvalues of the system. c) Write Matlab code to obtain matrix [s. I-A]-1. d) Results of (b) and (c) which are obtained by computer are as follows: At t=0 and V(t) is a step input having magnitude of 2. Find the Laplace transform of due to the initial conditions. e) Find the Laplace transform of q 1 due to the input. 2 V 2(t) t (s)

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS a) State variables are q 1, q 2 and . System of differential equations is arranged so as to 1 st order derivative terms are lefthand side and non-derivative terms are on the right-hand side. State variables A b) Matlab code which gives the eigenvalues of the system. A=[-1. 5 0; 0 0 1; 3. 75 -3. 75 0]; eig(A) c) Matlab code which produces [s. I-A]-1 clc; clear A=[-1. 5 0; 0 0 1; 3. 75 -3. 75 0]; syms s; i 1=eye(3); sia=inv(s*i 1 -A); pretty(sia) B

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS d) e)

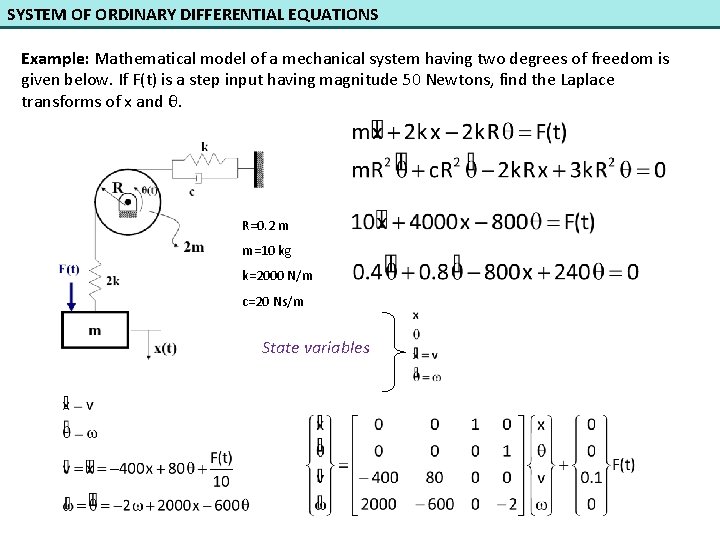
SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS Example: Mathematical model of a mechanical system having two degrees of freedom is given below. If F(t) is a step input having magnitude 50 Newtons, find the Laplace transforms of x and θ. R=0. 2 m m=10 kg k=2000 N/m c=20 Ns/m State variables

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS clc; clear A=[0 0 1 0; 0 0 0 1; -400 80 0 0; 2000 -600 0 -2]; syms s; eig(A) i 1=eye(4); sia=inv(s*i 1 -A); pretty(sia) If the initial conditions are zero, only the solution due to the input exists. Eigenvalues: System is stable since real parts of all eigenvalues are negative.

SYSTEM OF ORDINARY DIFFERENTIAL EQUATIONS